電動汽車充換儲一體化電站的優化調度策略及應用

葉 婷，鄧 星，黃 堃，梁加本，張智俊

（1.國網江蘇省電力有限公司 南京供電分公司，南京 210019；2.國電南瑞科技股份有限公司，南京 211100；3.南京郵電大學，南京 210023）

0 引言

伴隨新時代“能源革命”的推進，以電動汽車為代表的新能源為電網提供了源源不斷的能源供應。與此同時，電動汽車充放電的無序化、隨機化也給電網的運行管理帶來了巨大的挑戰。為此，如何對電動汽車進行精準預測并進行優化管理至關重要。通過對園區內電動汽車充換儲一體化電站、中斷負荷以及分布式發電源（distributed generator，DG）等重要元素進行集中監控管理，建立“區域協控虛擬電廠”典型模型，研究區域可調資源聚合技術，可下發實際調控指令，充分發揮電動汽車充換儲一體化電站和分布式電源的靈活調節能力，在兼顧個體利益的前提下，實現區域整體利益最大化。

文獻［1］針對電動汽車充電行為不確定性問題，建立了基于出行鏈理論的電動汽車出行及電池電量變化模型，提出了引入馬爾科夫決策過程的電動汽車用戶充電行為分析方法。文獻［2］提出了基于聚類分析的電動汽車充電負荷預測方法，在分析常規充電負荷影響因素并初步建立概率分布模型的基礎上，對每段行程的行駛里程和行駛時間構成的二維出行特征數據進行聚類分析。文獻［3］以出行時間和行駛里程確定且充電時間不受分時電價影響的電動公交車、出租車和公務車為研究對象，提出了一種根據某市現行峰平谷電價政策并綜合充電起始和結束時間所處的峰平谷階段動態修正充電目標的EV充電負荷預測方法。上述方法都能將不同層面的不確定因素考慮進電動汽車的用電預測過程中，在一定程度上改進了預測性能。但這些現有方法也存在不足:都只考慮了出行習慣，忽略了要綜合氣象數據、預報信息，對影響電動汽車用電需求的因素進行深入分析，從多個方面一起考慮，進而提升電動汽車的用電功率預測的準確性。

為了促進多能源互補及能源低碳化，文獻［4］提出了計及電轉氣協同的含碳捕集與垃圾焚燒虛擬電廠優化調度模型。針對VPP 內部風光資源的不確定性給其參與調峰市場帶來影響的問題，一些文獻對以VPP 為主體參與調峰市場開展研究。文獻［5］采取VPP 同時參與直接電力交易市場與調峰市場的運營模式，計及風光出力不確定性的影響，提出基于條件風險價值理論的VPP 日前優化運行模型，并利用Shapley值法對各成員聯合運行后取得的期望成本進行合理分配。但經分析可知，文獻［4］、文獻［5］著重解決風機、光伏等可再生電源參與虛擬電廠優化調度帶來的不確定性問題，對解決大量可再生能源的并網消納問題提供了很多有效方法。但這些文獻也存在不足:在虛擬電廠優化過程中，較少考慮電動汽車和新能源同時進行優化調度，且少有算法能快速有效地求解出調度策略，實現能量互補和削峰填谷。

本文研究的虛擬電廠的運營模式是指通過建立虛擬電廠控制模型，挖掘包括充換儲一體化電站、可中斷負荷和分布式電源的時空互補特性，并對其運行方式進行最優化控制，從而為電網提供輔助支撐服務。首先，綜合氣象數據、預報信息，對影響電動汽車用電需求的因素進行深入分析，實現對電動汽車的用電功率預測；其次，基于提出的改進粒子群算法，實現虛擬電廠的整體經濟效益最大化，通過最優化虛擬電廠各組成單元的運行方式，實現發用電互補，從而為電網的削峰填谷提供一定的支撐能力。

1 電動汽車負荷預測

電動汽車行駛活動具有很強的時空隨機性，為描述其動態行駛過程，引入了出行鏈的概念，通過記錄用戶日常出行的首次出行地點和行程結束地點，直至這兩個地點重合，形成一個完整的“鏈條”［6—9］。用戶的日常出行特征可以用出行鏈完整地反映出來，基于所提出的出行鏈對其充電需求進行分析，從而為其用電功率預測提供保障［8—9］。為了更好地了解出行鏈的概念，用虛線表示用戶出行的行駛過程，實線表示用戶出行的停車過程，實心點表示出行鏈的起點與終點，如圖1所示。

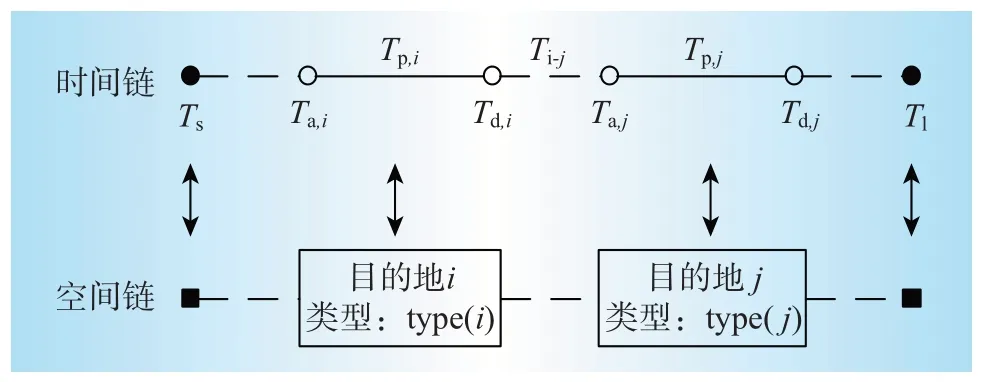
圖1 出行鏈示意圖Fig.1 Schematic diagram of travel chain

圖1 中，Ta,i、Td,i分別為到達、離開目的地i的時刻；Ta,j、Td,j分別為到達、離開目的地j的時刻；Tp,i為用戶在目的地i的停車時間；Ts、Tl分別為用戶出行鏈的起點、終點時刻；Ti-j為用戶從目的地i行駛至目的地j的花費時長。

1.1 出行鏈的時間分布

時間特征量在這次出行活動中滿足如下公式

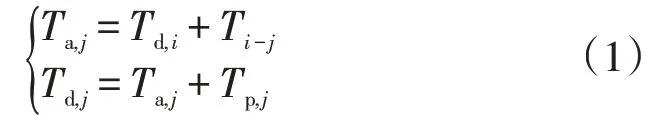
式中:Ta,i、Td,i分別為到達、離開目的地i的時刻；Ta,j、Td,j分別為到達、離開目的地j的時刻；Tp,i為用戶在目的地i的停車時間；Ti-j為用戶從目的地i行駛至目的地j的花費時長。

（1）首次出行時間概率分布

由文獻［9］可知，用戶每日出行鏈起點的時間概率密度f(t)服從正態分布，記作，其中，μs是出行鏈起點時間的均值，是出行鏈起點時間的方差，具體可以通過下式描述

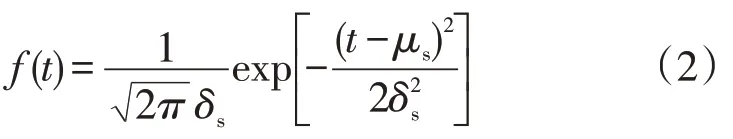
（2）電池荷電狀態分布和充電時長

設電動汽車在當前時刻T0的荷電狀態為SOC(T0)，則它在T時刻的荷電狀態SOC(T)，可以通過下式計算

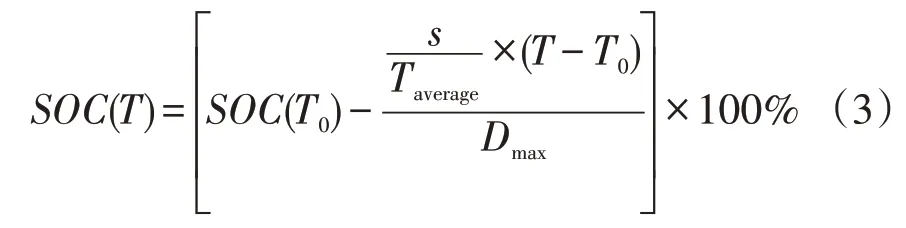
式中:s為T0時刻到T時刻的行使距離；Taverage為日行駛時間的平均值；Dmax為最大行駛距離。

一輛電動汽車的充電時長主要取決于其充電時長、其充電接口功率Pc、和其電池的荷電狀態，表示如下

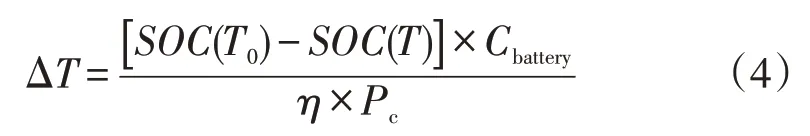
式中:Cbattery為電池容量；η為充電機的充電效率。

1.2 出行鏈的空間分布和充電時間的概率密度

由文獻［10］可知，用戶的出行鏈服從馬爾科夫鏈，即用戶下一時刻的出行地點只跟當前時刻的出行地點有關，并將用戶出行鏈中的每個地點表示為狀態，通過狀態之間的轉換表示其出行地點的變化。

記用戶車輛的狀態集為:{E1,E2,…,En}，用戶車輛從狀態Ei轉為狀態Ej的狀態轉移概率用pi-j表示，則pi-j滿足條件如下

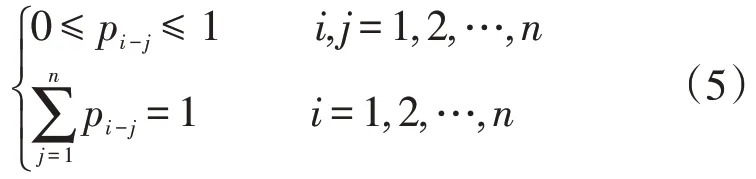
本文中，當前時刻用戶的行駛地點集合被構建為:{辦公區W，住宅區H，娛樂區E}，則用戶車輛從任一地點i行駛到下一個目的地j的狀態轉移概率Pi-j可以表示為

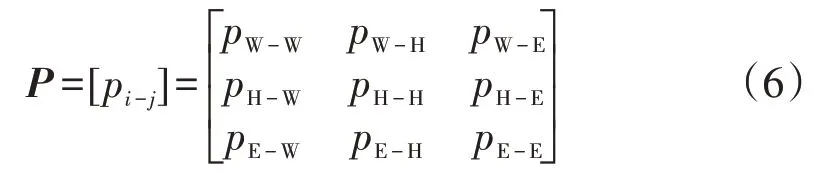
式中:fc(t)為起始充電時間的概率密度，則fc(t)基本服從分段正態分布［1］如下

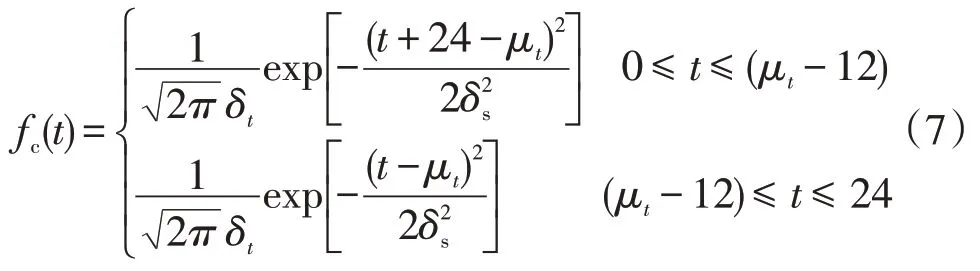
式中:μt、δt分別為充電起始時間的期望、方差。

1.3 電動汽車的負荷預測

基于上述對電動汽車時空特性的分析與建模，本文采用蒙特卡洛算法并綜合不同功能區的停車需求模型，得到其負荷曲線，從而實現電動汽車的負荷預測。

我們以第n輛電動汽車到達目的地i的情況為例進行分析:在電動汽車到達目的地的時刻Ti,s時汽車到達目的地并進行時長為ΔT的充電工作。由于起始充電時間與充電時長是相互獨立的參數，所以根據已知的電動汽車所需要的充電時長的概率密度，可以結合已知的不同充電方式下電動汽車起始充電時間的概率密度函數得到2 者的聯合概率分布函數Fs,c服從以下條件

式中:Fs為采用快速充電方式下起始時刻的概率密度函數；Fc為采用常規充電方式下起始時刻的概率密度。

進一步可以求得，在T時段，電動汽車充電的概率為

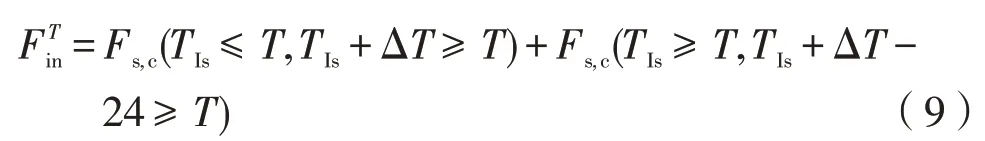
在T時段，令Eij(T)×Fck為采用常規充電方式的電動汽車數量，Eij(T)×Ffk為采用快速充電方式的電動汽車數量。則采用常規、快速充電方式的負荷Qi-j,c(T)、Qi-j,f(T)可計算如下

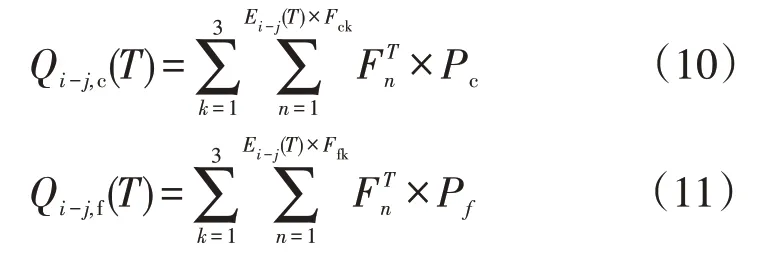
式中:Pc為常規充電功率；Pf為快速充電功率。

基于式（10）、式（11），在T時段，電動汽車總負荷Qi可以由下式進行計算

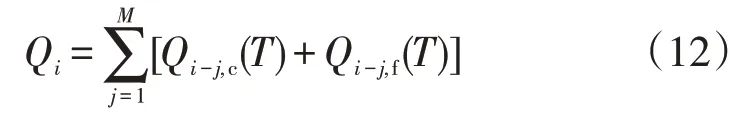
式中:Qi-j,c(T)為常規充電方式下電動汽車從地點i行駛至地點j對應的充電負荷；Qi-j,f(T)為快速充電方式下電動汽車從地點i行駛至地點j對應的充電負荷。

基于上述各時段電動汽車的負荷預測，結合電動汽車充換儲一體化電站的儲能容量，即可獲得電動汽車充換儲一體化電站可調度最大容量。

2 基于電動汽車預測的源荷儲協同調度策略

基于園區內電動汽車充換儲一體化電站、中斷負荷以及分布式發電等重要可調控單元，建立“區域協控虛擬電廠”典型優化模型。

2.1 優化目標函數

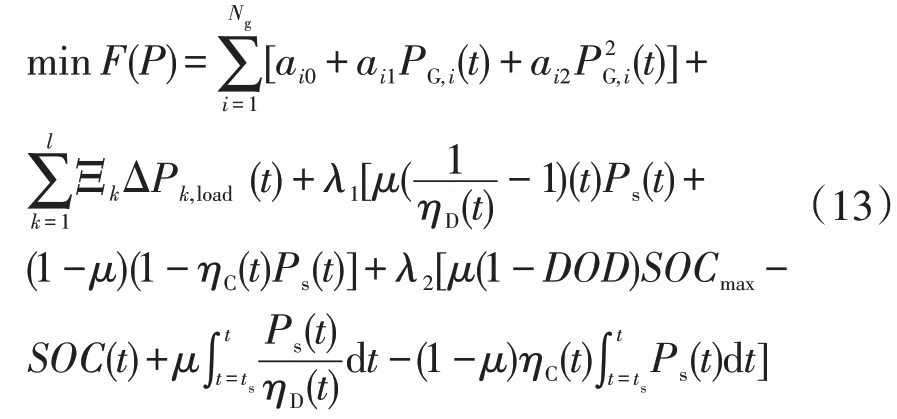
式中:F(P)為目標函數，即整個虛擬電廠的運行成本；Ng為分布式電源個數；ai0、ai1和ai2為成本系數；PG,i(t)為第i個分布式單元在t時刻的出力；ΔPk,load(t)為第k個可中斷負荷；Ξk為第k個可中斷負荷賠償成本；λ2為電池的損耗成本；ts為運行初始時刻；ηc(t)、ηD(t)分別為電動汽車充換儲一體化電站在t時刻的充、放電效率，放電時μ=1，充電時μ=0；DOD為放電深度；SOC(t)為電動汽車充換儲一體化電站在t時刻的荷電狀態；SOCmax為電動汽車充換儲一體化電站最高荷電狀態；Ps(t)為電動汽車充換儲一體化電站在t時刻的調度功率。

（1）約束條件

功率平衡約束

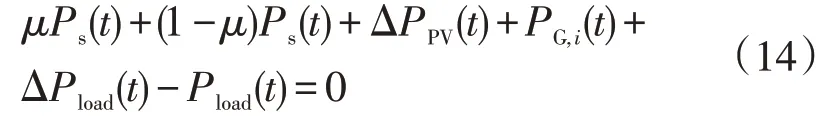
式中:ΔPload(t)為可中斷負荷；Pload(t)為負荷在t時刻的預測功率；PPV(t)為負荷在t時刻的光伏發電功率，μ代表放電狀態，放電時μ=1，充電時μ=0。

發電機組出力約束

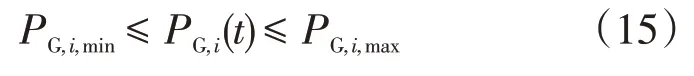
式中:PG,i,min為發電機組出力的最小值；PG,i,max為發電機組出力的最大值；PG,i為發電機組出功。

可中斷負荷出力約束

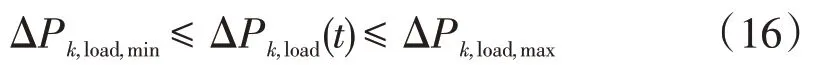
式中:ΔPk,load,max、ΔPk,load,min分別為可中斷負荷的最大值、最小值；ΔPk,load(t)為t時刻的可中斷負荷出力。

儲能充放電約束

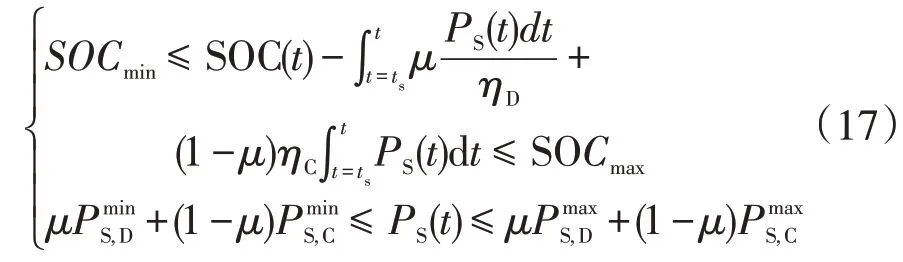
爬坡率約束

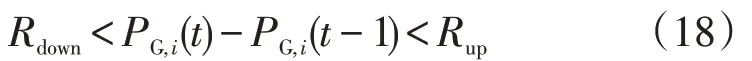
式中:Rdown為爬坡率的下限；Rup為爬坡率的上限。

2.2 優化目標函數求解

對于模型的求解，采用改進的粒子群的優化方法。

在園區虛擬電廠經濟調度優化模型中，關于等式約束的處理，采用動態處理的方法，使得每個粒子在尋優的過程中可以始終滿足等式約束。具體過程如下［11—12］:

①優先設置索引時間段t以及粒子群算法尋優過程初始化系數（粗調系數Jcoarse、細調系數Jfine），其具體值如下

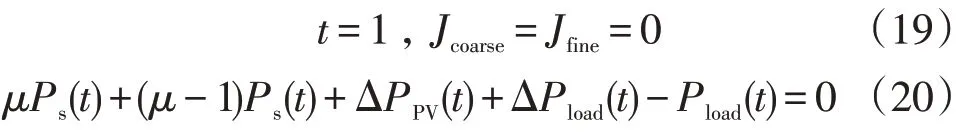
式中:μ為充放電狀態，放電時μ=1，充電時μ=0；Ps(t)為電動汽車充換儲一體化電站在時刻的調度功率；ΔPPV(t)為t時刻的光伏出功變化量；ΔPload(t)為t時刻的負荷需求變化量；Pload(t)為t時刻負荷初始需求量。

總功率差ΔP可以由式（20）獲得，如果ΔP滿足在允許的總的功率差ε的范圍，轉至步驟⑤，否則，進行步驟②。

通過式（2）可以獲得發電機組在每個時間段內的發電需求功率，并基此進行調整，檢查是否發電機組，其中分別是第i個發電機組的功率額定上、下限。在有Ns個發電源的系統中，調整后第i個電源的出功PG,i(t)為

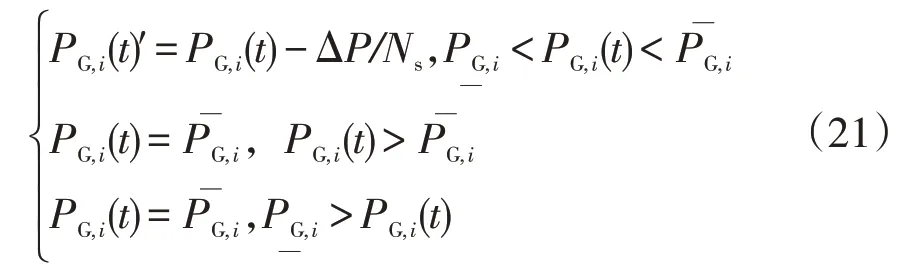
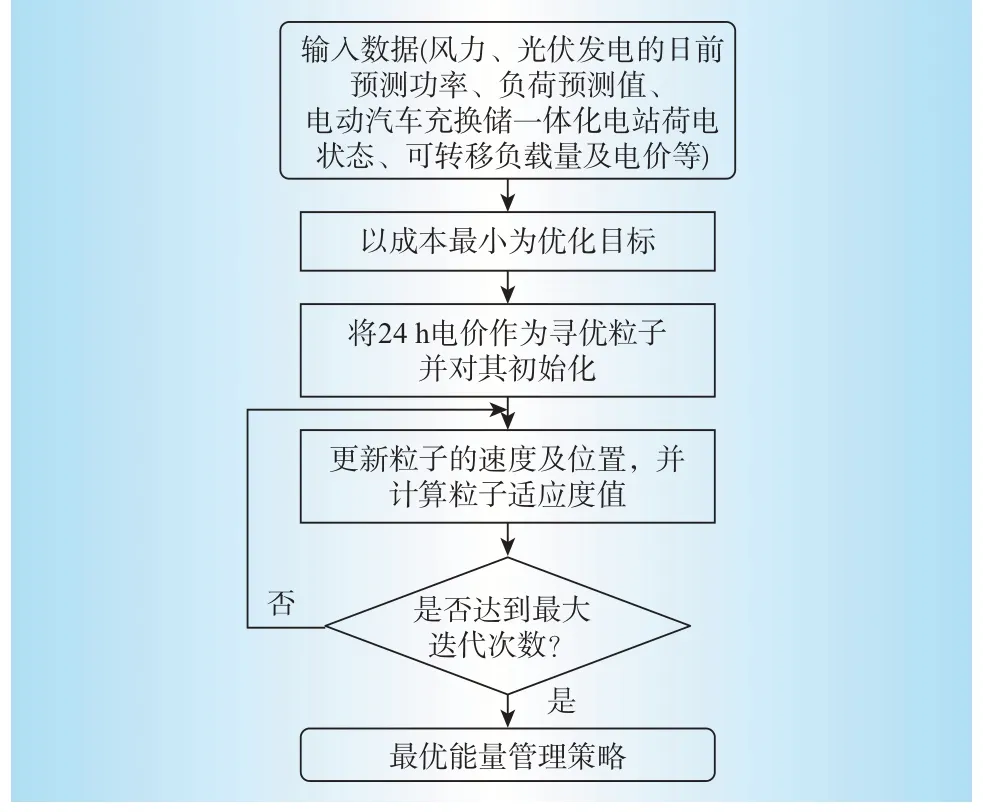
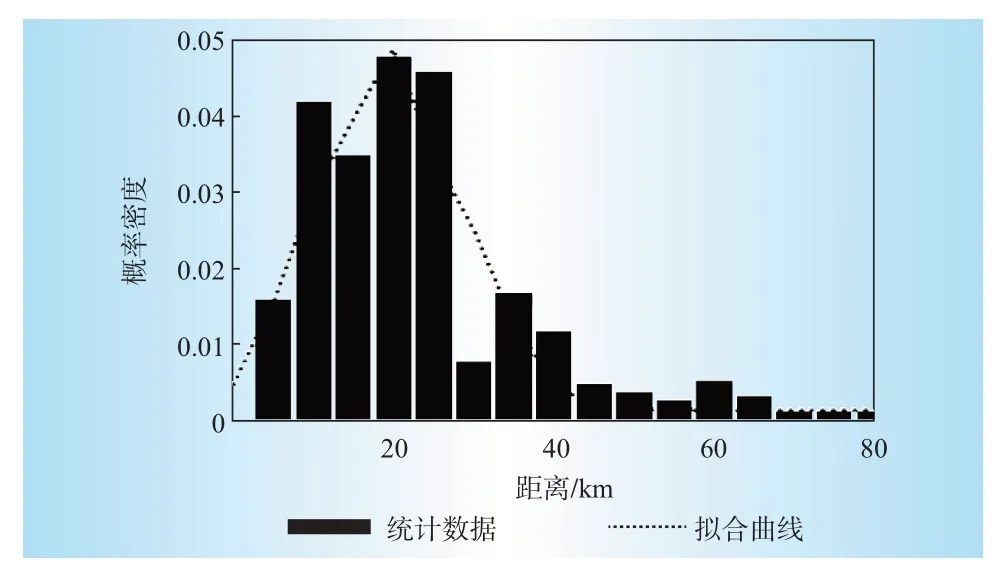
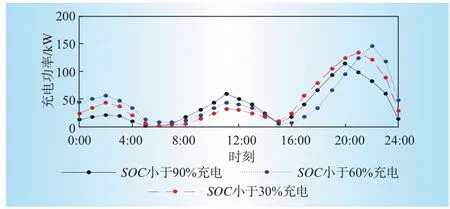
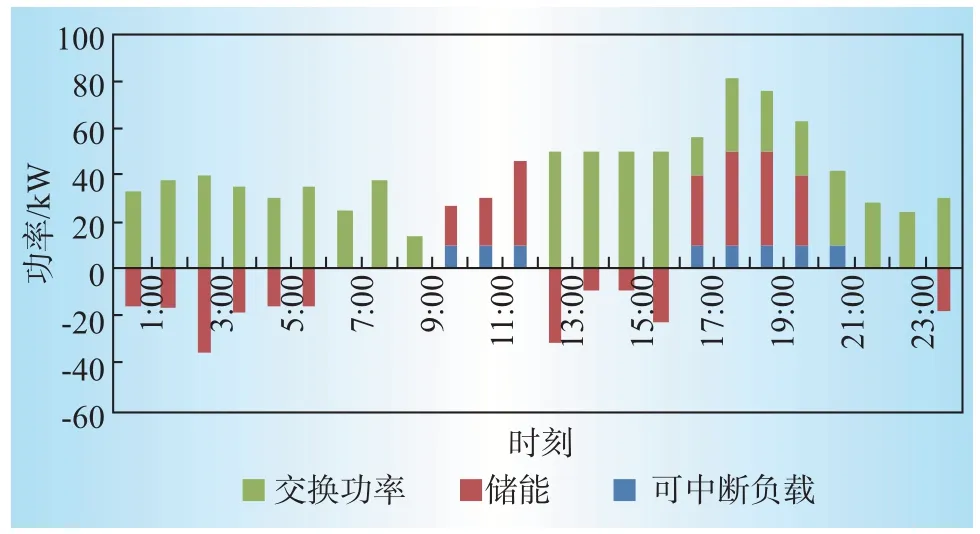
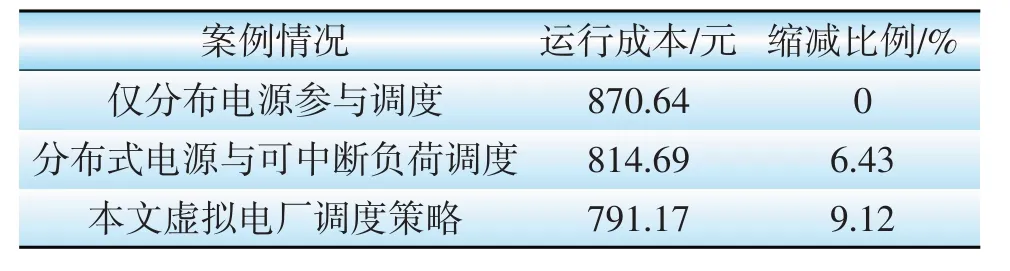
②若粗調系數Jcoarse低于粗調系數上限Jmax，即Jcoarse

③利用Ns個發電機組中選擇的一個隨機指數r，結合式（8）中得到的總的功率差，通過式（10）對每個發電機組的輸出功率進行調整，并執行步驟④。

④若細調系數Jfine低于粗調系數上限J'max，即Jfine

⑤如果t

基于粒子群算法能夠很好的解決提出的電網經濟調度模型。

求解流程如圖2所示。

圖2 電動汽車負荷預測流程Fig.2 Electric vehicle load forecasting flow

3 仿真驗證

本文將根據前面所述的模型，對某市經濟開發區的電動汽車充放電進行預測，表1給出了不同用地的使用情況。而仿真平臺主要采用windows7操作系統的高性能計算機。主要配置四核CPU、2.5 GHz主頻、16 G內存、500 GB 硬盤。主要的仿真軟件為MATLAB/simulink2013a軟件。本節電動汽車數據來源于（2021版）江蘇省南京市新能源汽車產業投資布局分析報告與《南京市打造新能源汽車產業地標行動計劃》。對于風機、光伏、儲能和可切負載的數據則是借鑒文獻［13］和文獻［14］中的相關數據人為選定的。對這些數據而言，可以進行變更，只需在算法中將相關數據對應替換即可，并不影響優化問題的求解過程。

表1 不同用地的相關參數Table 1 Relevant data of different areas

按照該市發展電動汽車的規劃，預計到2030年，該市電動汽車的保有量大概為5.2 萬輛。根據對該地區私家車日出行情況的調研，可知車輛的日均行駛距離為37.85 km。圖3表示的是車輛從辦公區到住宅區之間行駛距離的擬合情況，原始數據直接從園區的歷史記錄中獲取。

圖3 電動汽車預測結果對比Fig.3 Comparison of electric vehicle prediction results

通常情況下，不同用戶的充電行為不相同，使得電動汽車的空間分布不同。電動汽車充電前剩余SOC閾值分別為90%、60%、30%時，住宅區私家車負荷曲線如圖4所示。

圖4 不同充電SOC 閾值選擇下的負荷曲線Fig.4 Load curves in different charging SOC situations

由圖4分析可知，住宅區的負荷一般高于辦公區和娛樂區負荷。住宅區有2 個負荷高峰，隨著選擇SOC 閾值的降低，負荷由中午向夜晚轉移。由此可得，電動汽車的充放電受用戶充電行為所影響。

圖5表示在圖3所示的電動汽車接入情況下，含有電動汽車充換儲一體化電站（正為放電，負為充電）、儲能設備和可中斷負載的調控量。設定在該仿真模型中，電動汽車充換儲一體化電站、儲能設備、可中斷負荷及分布式電源所對應的最大容量分別為100 kW、60 kW、20 kW和10 kW。其中，9:00—11:00無exchange power 就代表該時間段內僅靠分布式電源出力（該階段光伏出功與風機出功都足夠大）與和儲能設備出力，即可滿足負載需求。圖5 中對應各時間點的優化調度策略如下:對于風光等可再生能源而言，始終運行于最大功率點跟蹤模式。充換儲一體化電站在1:00—8:00、12:00—23:00都處于供電狀態；儲能設備在0:00—5:00、12:00—15:00 和23:00都處于充電狀態，在6:00—8:00和16:00—19:00都處于放電狀態，其余時間點既不充電也不放電；可中斷負載在9:00—11:00 和17:00—20:00 都處于被切除狀態，在其余狀態都處于連接狀態。

圖5 日經濟優化調度值Fig.5 Daily economy optimal dispatch value

表2 表示在表1 和圖3 所示的電動汽車接入情況下，該系統分別在僅分布電源參與調度，分布式電源與可中斷負荷調度，本文虛擬電廠調度策略等3類情況下的運行成本。

表2 調度策略運行成本比較Table 2 Cost comparison of scheduling strategies

從表2 可以看出，基于本文提出的虛擬電廠優化調度策略，該系統的用電運行成本降低了9.12%，運行更加經濟。

4 結束語

本文提出一種針對電動汽車充換儲一體化電站、可中斷負荷以及分布式電站組成的虛擬電廠，以經濟效益最大化為目標構建綜合目標函數，通過確定電動汽車充放電功率大小、儲能電池充放電策略和可中斷負荷的調度策略，保證了多種微電源組合下經濟、高效和低碳運行。該虛擬電廠模式正常情況下為一種純用能負荷，也具備向電網反向饋電的能力，在形成一定規模的情況下，可作為一種高效率儲能系統，實現調度層面削峰填谷、應急支撐的功能。該研究為打造國家電網公司區域協調控制系統虛擬電廠功能應用“可實行、可復制、可推廣”的典范提供了理論依據。