多源航跡數據融合系統的模糊關聯算法應用研究

黃濤 水孝敏

摘要：隨著我國民航事業的高速發展，為空中交通管制提供數據的通信導航監視設備種類和數量越來越多，如何將多源數據更有效地進行融合處理成為迫切需要解決的問題，本文針對其中核心算法之一的航跡關聯，從處理架構設計、算法原理和評價準則入手，詳細描述了模糊關聯法的具體應用方法，并對測試結果進行評價后給出了基于參考目標拓撲矩陣的改進算法，最后對需深入研究的內容進行了探討。

關鍵詞：多源數據;數據融合;模糊關聯

中圖分類號：TP393? ? ?文獻標識碼：A

文章編號：1009-3044（2021）16-0005-03

開放科學（資源服務）標識碼（OSID）：

空中交通管理通常依賴多源航跡數據經融合后形成的系統航跡來實施管制。目前大中型空中交通管理自動化系統接入的航跡數據不僅數量多且種類也較多，如一/二次監視雷達、ADS-B、場監雷達和多點定位等[1]。如果監視源數據質量下降（諸如交織交疊、反射、丟點和遮擋等異常）將影響管制運行效率，甚至會危及飛行器安全，因此研究并改進多源航跡數據融合系統顯得尤為必要，多源航跡關聯算法是其中關鍵的核心算法之一。

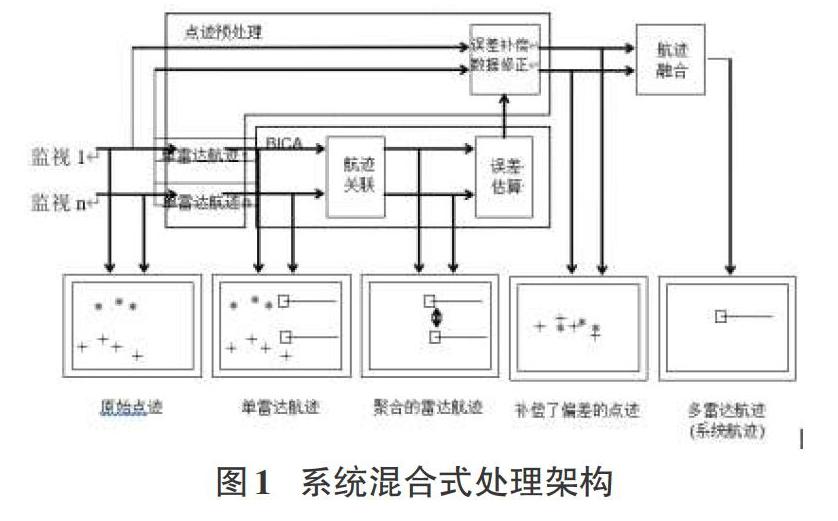
1 系統處理架構

為了有效地驗證各個算法模塊，必須設計一個適合本系統實際數據源的處理架構，通常有三類[2]：

1） 集中式：同一時刻的所有數據發送至融合中心進行處理，好處是融合性能最優，缺點是中心運算負荷大、通信帶寬高;

2） 分布式：先各自進行航跡處理后將本地航跡發送至融合中心進行處理，好處是中心運算負荷小、通信帶寬低、魯棒性高，缺點是原始信息有所缺失，在一定程度上降低了融合性能;

3） 混合式：兼具上面兩類的優點，對中心的運算能力和通信帶寬都有比較高的要求，但從能效比綜合考慮是最好的。

圖1給出了本系統采用的混合式處理架構：

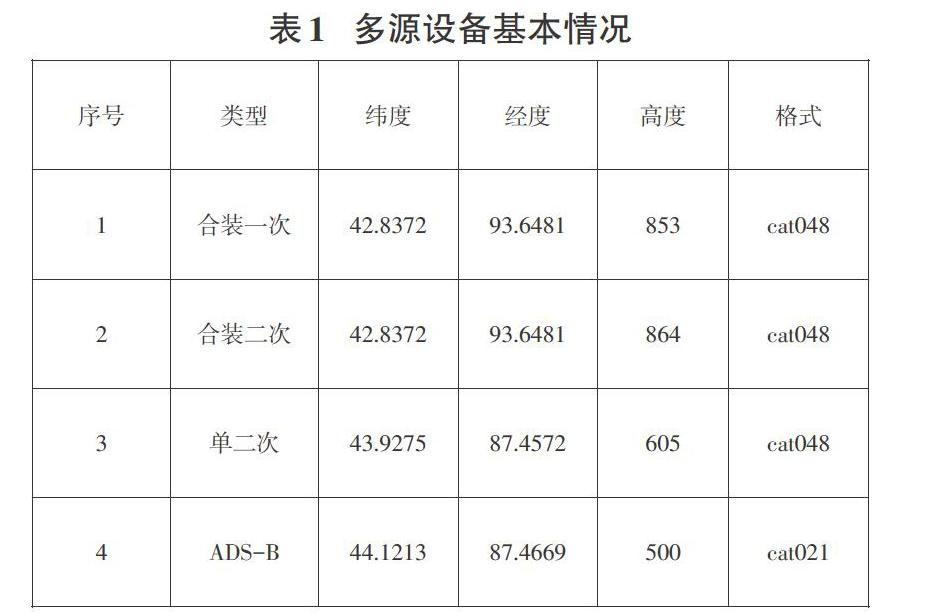
表1為測試數據來源的新疆4部設備基本情況：

2 航跡關聯

航跡關聯的實質是航跡匹配，由于存在多種不確定性，包括各設備自身的系統誤差、隨機誤差以及來自內外部的雜波干擾，都將帶來匹配問題。

經典的航跡關聯算法大多以假設傳感器數據通過濾波或標校后只含觀測噪聲，算法得到的是基于此假設的多傳感器數據集合的最優匹配結果，基于統計理論的最近鄰域法、貝葉斯法和D-S法等[3]，利用經典的狀態估計及協方差矩陣等信息確定關聯匹配，但是在多個觀測目標聚集或虛警較嚴重時，可能會出現關聯錯誤或遺漏情況;引入模糊理論后，多觀測目標間的位置、速度、航向的差異都可作為新因素，在一定程度上解決關聯算法中各種偏差導致的模糊性問題，為適應多源航跡融合所面臨的復雜環境中關聯問題提供了一個很好的解決思路。

3 關聯性能的評價方法

評價方法選用了模式識別中使用的Precision-Recall-F1方法[4]，具體如下：

TP：真數據已關聯，目標匹配正確;

FP：真數據未關聯，新目標;

TN：假數據已關聯，目標匹配錯誤;

FN：假數據未關聯，虛警;

Precision = TP / （TP + FP）;

Recall = TP / （TP + FN）;

F1 = 2*Precision*Recall/（ Precision+Recall）

Precision給出關聯的正確率，Recall給出正確航跡的識別成功率，F1給出綜合性能。

4 模糊航跡關聯法

模糊航跡關聯為關聯過程中各因素分別確定隸屬度函數以表征待關聯航跡對在該因素的關聯度，總關聯度為各個因素關聯度的加權和。該判決結果由模糊因素集合[Ukk=1，k][Ukk=1，k]，組成，各因素對應的隸屬度函數（典型函數包括正態型分布，居中型分布，降T型分布等）定義為[μkukε0，1]，加權系數為[ak]，且滿足[kak=1]，最終各航跡之間的相似度[Si，j]為[kakμkuk]，對來自[K]部雷達的所有航跡便構成了當前時刻下的[K]階模糊關聯矩陣。有了矩陣后，便可尋找最佳的全局解，我們采用的方法是最大綜合相似度判別準則，具體步驟如下：

1） 尋找矩陣中最大的元素[Si，j]，如果大于門限值，則可判定航跡[i，j]為關聯對;

2） 消去該元素所在的行列，矩陣將下降1階;

3） 重復1）和2）直到矩陣全部消去。

在此方法中，每個因素的加權系數體現各因素的影響程度，所以因素和隸屬度函數的選取是應用中需重點關注的內容，我們選取了位置、航向和航速構成模糊因素集，正態型分布型為隸屬函數，將時間段為1個小時的3組數據進行測試，結果如表2所列：

從F1可以看到在不同的時間段差異較大且不夠理想，但模糊航跡關聯方法最大的好處就是對各因素沒有做任何限制，這就為我們在關聯判決過程中利用更多的信息因素提供了改進的空間。

5 改進的模糊航跡關聯法

5.1 方法概述

針對系統偏差較大且受到一定干擾的航跡關聯場景，我們引入新的因素——目標參照拓撲，即待關聯飛行器周邊的其他飛行器作為參照物，利用他們之間的空間拓撲信息通過模糊航跡關聯方法在處理此類非高斯分布的因素，可實現更好的航跡關聯效果。

5.2 提取拓撲矩陣

為描述參照物的拓撲矩陣，需對參照拓撲進行提取，即構造參照物的拓撲矩陣。對于一個待關聯目標，按照設備觀測目標的特點確定采用什么樣的坐標系，且維度最多可定義為三維。我們按照雷達的特點，以目標為中心，設定極坐標區域進行劃分：沿直徑等分S個圓環，方位等分T個扇區，這樣參照區域就由S*T個單元組成。拓撲矩陣中元素值將對應單元目標存在可能性，為每個單元[Rij]分配適當的隸屬度[Uij]，i、j分別為徑向和方位的劃分，通常約定該區域無參考目標時[Uij]為0，對應區域存在參考目標時0<[Uij]≤1。圖2表述劃分的示意過程：

5.3 拓撲矩陣的彌散化處理

隨機誤差（如系統差和觀測噪聲）是待關聯航跡不確定性的主因。通常航跡經過數據源本地標校和濾波處理后，上述不確定性的影響已經大大減小，只要單元大小設置合適，待關聯航跡對的位置應在同一單元內，拓撲矩陣就不會改變。彌散化處理降低了隨機誤差對航跡關聯性能的影響。

航跡間的方位偏差反映矩陣中同一行的相鄰位置上，且無論參照物在極坐標上的距離如何，落入同行相鄰單元的可能性基本相同。距離偏差于此基本一致，不同的是反映到列上。

為應對此問題，需對拓撲矩陣做彌散化處理。當矩陣中的某一單元值為1時（即確定存在目標），需在其周圍單元增加彌散化系數m（0

圖3? ?彌散化過程示意圖

5.4 基于拓撲矩陣的模糊關聯

經彌散化后的拓撲矩陣實質上是參照目標在空間拓撲信息抽象成一種模糊數學表達，航跡關聯就是將待關聯航跡對的拓撲矩陣進行關聯度（即相似程度）計算，找出最為匹配的航跡對。

考慮計算的方便性，將矩陣的第t行放在待觀測目標向量的第t個分量上，在k時刻，[va]，[vb]分別表征雷達A，B的待關聯航跡拓撲向量集中的任意兩個向量，即代表兩部雷達同時刻觀測到的任意兩條航跡。由此獲得關聯度函數如下：

關聯度的大小反映兩條航跡相似程度，經過彌散化后，如果兩個參照拓撲中目標不在同一單元內，盡管相隔很近，關聯度仍然不為0，為簡單起見以兩個單點拓撲（即只包含一個參照目標）舉例說明，分兩種情況計算關聯度：

（1）兩點間隔為1個單元

[νa=0，0.1，1，0.1，0]? [νb=0，0，0.1，1，0.1]

[Sνa，νb=0.196]

（2）兩點重合

[νa=0，0.1，1，0.1，0] [νb=0，0.1，1，0.1，0]

[Sνa，νb=1]

此時可設定一個門限值[St]，當[Sνa，νb

6 思考

通過對基于參考目標拓撲矩陣的改進型模糊關聯算法的實現機理和實際應用過程的應用與分析，我們認為有以下幾個方面需要關注：

1）參考目標拓撲區域的確定

在拓撲中的參考目標數越多，可提供的拓撲信息就越豐富，匹配過程中獲得的相似度的可信程度就越大。但當單元格固定時，參照區域的擴大會導致計算量的增加，如何平衡運算負荷與系統性能值得進一步研究;

2）拓撲單元格的劃分

單元格劃分的精細程度實際上決定了系統對拓撲信息的分辨力。因此區域內的目標個數、疏密程度與劃分的拓撲單元大小有著直接的關聯;

3）彌散化系數的確定

彌散化系數是對系統中各種不確定性的表征。雷達系統的性能（如隨機誤差等）與具體拓撲單元的大小將共同決定彌散化系數的大小，他們之間的最優量化關系式也需要繼續研究。

7結束語

本文給出了基于參考目標拓撲矩陣的模糊航跡關聯算法實際應用的方法，通過對結果分析得出采用此類模式識別算法，將模糊貼近度作為相似性的度量，使得關聯過程更貼近了人腦的工作模式，可獲得更好的關聯結果。綜上所述，該算法具有較好的推廣應用價值。

參考文獻：

[1] 柴昱.自動化系統中多雷達數據融合子系統的研究與實現[D].成都：電子科技大學，2010.

[2] 楊露菁，余華.多源信息融合理論與應用[M].2版.北京：北京郵電大學出版社，2011：13.

[3] 祁友杰，王琦.多源數據融合算法綜述[J].航天電子對抗，2017，33（6）：37-41.

[4] 王成，劉亞峰，王新成，等.分類器的分類性能評價指標[J].電子設計工程，2011，19（8）：13-15，21.

【通聯編輯：梁書】