直通式全玻璃真空集熱器熱性能研究
李國帥, 羅顯峰, 趙丹丹, 鞏景虎, 李亮光
(1. 東南大學 江蘇省太陽能技術重點實驗室, 南京 210096;2. 南京嘉業新能源有限公司, 南京 210096)
傳統式U形全玻璃真空集熱管易生產、價格低,被廣泛用于太陽能熱水系統,但工質流動是由浮力和熱虹吸作用產生的,因此傳熱效率低[1]。為了提高太陽能熱水系統真空管的熱性能,路靈等[2]發明發了一種熱動力自然循環非承壓式太陽能熱水系統導流裝置,改善了現有太陽能熱水系統真空管導熱不暢、易炸管等問題。陳雪嬌等[3]對導流管式全玻璃真空管太陽能熱水系統熱性能進行測試研究,證明該系統具有熱性能良好、傳熱量高、平均熱損因數小、太陽能熱轉換率更高等優勢。沈亞蘭等[4]得出波紋式全玻璃真空管熱性能優于傳統式全玻璃真空管,熱效率高出5.2~8.1百分點。
筆者提出了一種新型集熱器,即直通式全玻璃真空集熱器,其集熱管由內管和外管2根玻璃管組成,管的兩端分別密封在一起,中間形成真空區域,內管的外表面涂覆有太陽能吸收層,工質從玻璃內管的一端流到另一端,并在此過程中吸收熱量。與傳統式U形全玻璃真空集熱器相比,工質流動變為湍流,改善了傳熱方式,系統熱性能得到很大提高[5]。
筆者對單根集熱管進行傳熱分析,建立一維傳熱數學模型,借助MATLAB軟件采用假設溫度法迭代求解,分析集熱器熱性能的影響因素。通過動態測試方法對模型進行驗證,并以對比實驗證明直通式全玻璃真空集熱管熱性能優于傳統式。
1 模型建立
集熱管的傳熱是一個復雜的耦合傳熱過程,包括輻射、對流及導熱[6-7],對于處于穩態的真空集熱管,其散熱過程是熱量先經玻璃內管外壁以輻射、對流形式傳遞給玻璃外管內壁,再經玻璃外管內壁以導熱形式傳遞,最后由玻璃外管外壁以輻射、對流形式向外散熱到環境。基于熱力學定律和集熱管的能量流動,參照文獻[8]可建立直通式真空集熱管的一維傳熱模型(見圖1)。模型假設為:(1)集熱管傳熱達到穩態;(2)集熱管的軸向溫度分布均勻;(3)忽略集熱管向端部和支架的散熱影響。
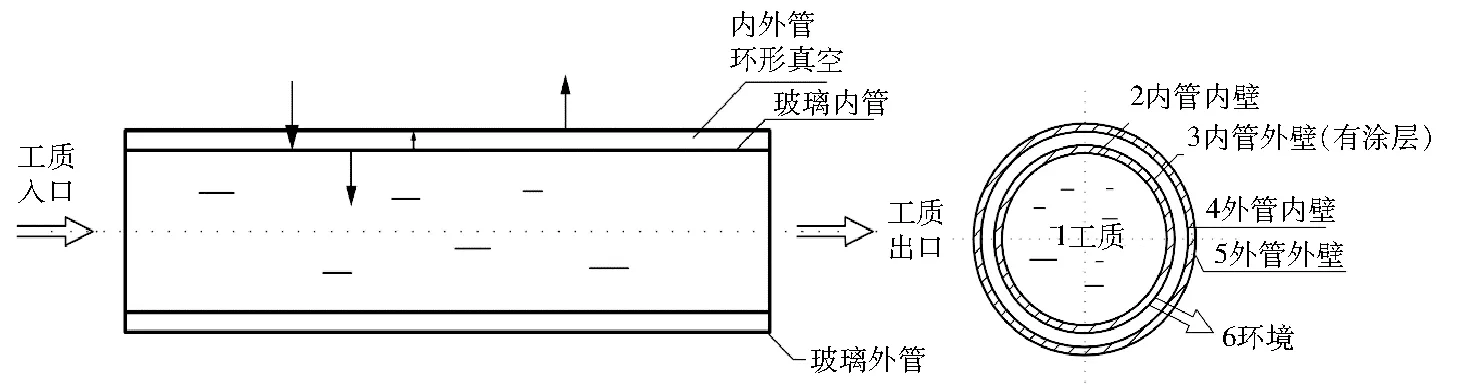
圖1 一維傳熱模型簡圖
1.1 玻璃內管外壁到玻璃內管內壁的導熱傳熱
根據傅里葉定律可得:
(1)
式中:Q23cond為玻璃內管外壁與內壁之間的導熱傳熱量,W/m;T3為玻璃內管外壁溫度,K;T2為玻璃內管內壁溫度,K;D3為玻璃內管外直徑,取0.047 m;D2為玻璃內管內直徑,取0.043 m;λ23為玻璃內管在溫度T23(T23=(T2+T3)/2)下的導熱系數,W/(m·K)。
1.2 玻璃內管內壁到工質的對流傳熱
根據玻璃內管內壁及工質的溫度,由牛頓冷卻公式可以計算出對流傳熱量為:
Q12conv=πh12D2(T2-T1)
(2)
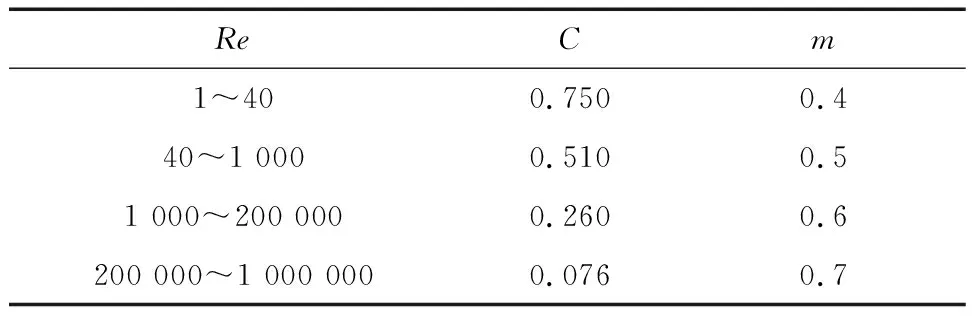
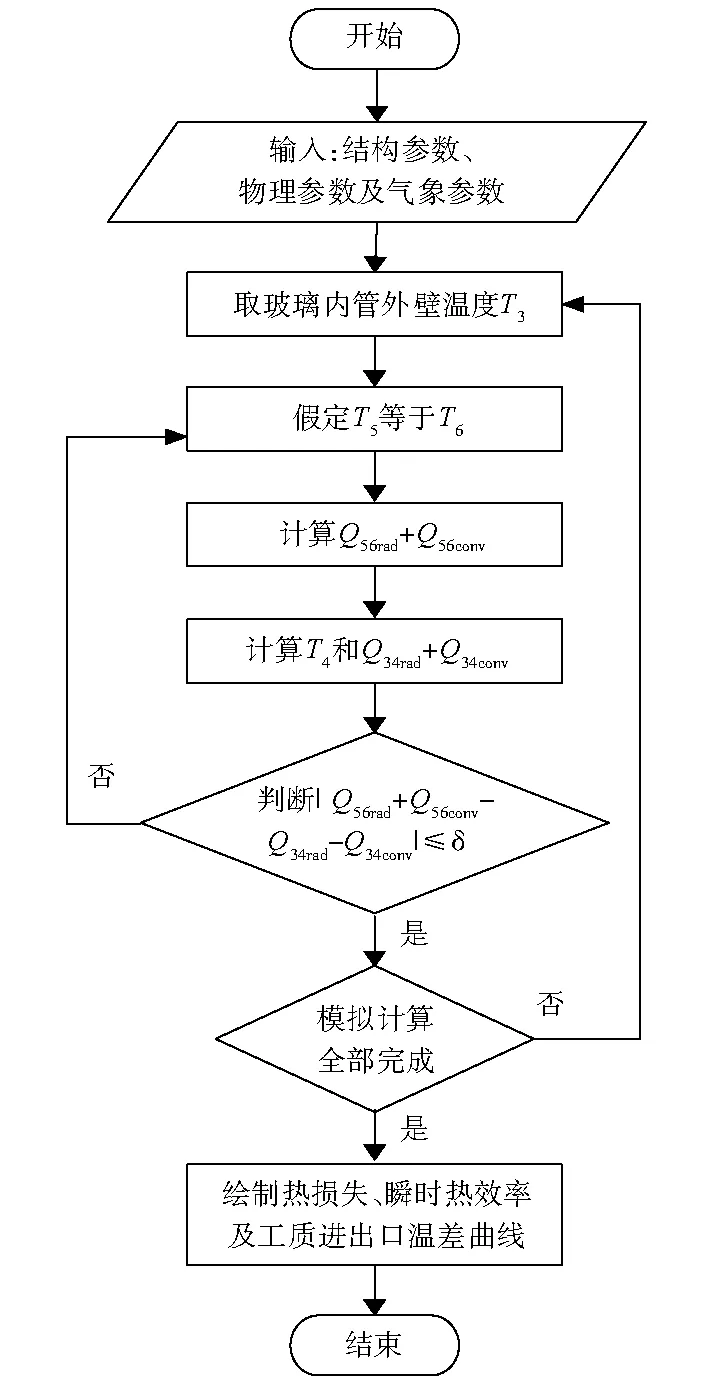
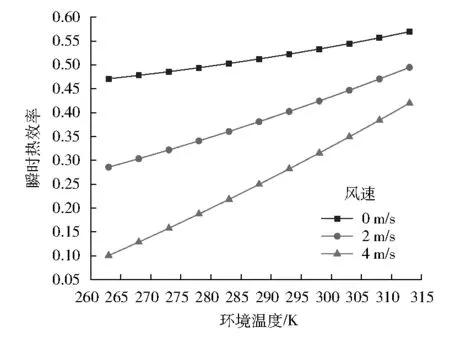
式中:Q12conv為玻璃內管內壁與工質的對流傳熱量,W/m;T1為工質溫度,K;h12為工質在溫度T12(T12=(T1+T2)/2)下的對流傳熱系數,W/(m2·K);k12為工質在溫度T12下的傳熱系數,W/(m·K);Pr1、Pr2分別為工質在溫度T1、T2時所對應的普朗特數;ReD2為玻璃內管內徑雷諾數;NuD2為玻璃內管內徑努塞爾數,工質流體處于紊流狀態時,0.5 玻璃內管外壁到玻璃外管內壁為灰體表面輻射傳熱,其傳熱過程計算公式為: (3) ε23=0.048+0.000 32T23 式中:Q34rad為玻璃內管外壁與玻璃外管內壁的輻射傳熱量,W/m;T4為玻璃外管內壁溫度,K;D4為玻璃外管內直徑,取0.054 m;σ為斯忒藩-玻耳茲曼常數,為5.67×10-8W/(m2·K4);ε23為選擇性吸收涂層在溫度T23的發射率;ε45為玻璃管的發射率,取0.9。 環形空間氣體壓力對真空集熱管的傳熱方式影響較大,根據不同的氣體壓力進行討論。 (1) 當氣體壓力<133.32 Pa時,內外玻璃管間的傳熱是分子導熱傳熱,其計算公式為: Q34conv=πD3h34(T3-T4) (4) 式中:Q34conv為玻璃內管外壁與玻璃外管內壁的對流傳熱量,W/m;h34為環形空間氣體在溫度T34(T34= (T3+T4)/2)下的對流傳熱系數,W/(m2·K);k34為環形空間氣體在溫度T34下的傳熱系數,W/(m·K);a為適應系數;b為相關系數;x為交互因子;ξ為分子碰撞的平均自由程,cm;y為環形空間氣體的比熱容比;Γ為環形空間氣體的分子直徑,cm;p為氣體壓力,Pa。 (2) 隨著環形空間的氣體壓力增大,氣體分子漸漸進入連續介質狀態,內外玻璃管間的傳熱為對流傳熱[9],當氣體壓力≥133.32 Pa,其計算公式為: (5) 式中:Pr34為環形空間內氣體在溫度T34下的普朗特數;RaD3為在金屬吸熱管外徑條件下的瑞利數;α34為環形空間內氣體在溫度T34下的熱擴散系數,m2/s;v34為環形空間內氣體在溫度T34下的運動黏度,m2/s;β34為環形空間內氣體在溫度T34下的體膨脹系數,K-1;g為重力加速度,m2/s。 通過圓形玻璃層的導熱可以利用傅里葉定律來計算,具體公式為: (6) 式中:Q45cond為玻璃外管內壁與玻璃外管外壁的導熱傳熱量,W/m;T5為玻璃外管外壁溫度,K;D5為玻璃外管外直徑,取0.07 m;λ45為環形空間內氣體在溫度T45(T45=(T4+T5)/2)下的導熱系數,W/(m·K)。 根據牛頓冷卻公式,可以計算出玻璃外管與周圍空氣之間的對流傳熱量為: Q56conv=h56(T5-T6)πD5 (7) 式中:Q56conv為玻璃外管外壁與周圍空氣的對流傳熱量,W/m;T6為環境溫度,K;k56為環形空間氣體在溫度T56(T56=((T5+T6)/2)下的傳熱系數,W/(m·K);NuD5為玻璃外管外徑條件下的努塞爾數,根據無風和有風分類討論。 (1)無風情況下,玻璃外管外壁與環境的傳熱方式為自然對流傳熱,NuD5取平均努塞爾數: (8) 式中:RaD5為在玻璃外管外徑條件下周圍空氣的瑞利數;Pr56為集熱管在溫度T56下周圍空氣的普朗特數;α56為集熱管在溫度T56下周圍空氣的熱擴散系數,m2/s;v56為集熱管在溫度T56下周圍空氣的運動黏度,m2/s;β56為環內氣體在溫度T56下的體膨脹系數,K-1。 (2)有風情況下,NuD5可以按照橫掠單根圓柱管的平均努塞爾數計算: (9) 式中:ReD5為玻璃外管外徑條件下的雷諾數;Pr5為玻璃外管外壁溫度條件下的普朗特數;Pr6為環境溫度條件下的普朗特數;C、m的取值見表1。 表1 橫掠單根圓柱管C、m的取值 假設集熱管是一個小型凸面物體,其凈輻射傳熱量為: (10) T7=T6-8 式中:Q57rad為玻璃管外壁與天空的輻射傳熱量,W/m;T7為天空溫度,K。 集熱管得到的太陽輻射能為: Qsun=IAsηopt (11) 式中:Qsun為集熱管吸收到太陽的輻射量,W;I為投射到集熱管上的太陽直射輻射強度,W/m2;As為集熱管采光面積,m2;ηopt為集熱管的光學效率;kθ為入射角修正系數;θ為太陽輻射入射角,rad;esh為直通式真空集熱管有效長度系數,取0.974;ege為幾何修正系數,取0.98;eda為集熱管干凈度修正系數,取0.965;eun為不確定修正系數,取0.96。 通過傳熱過程分析,忽略Q34conv,且在無風的環境下運行,可得運行過程中的熱損失QL為: QL=Q34rad=Q45cond=Q56conv+Q56rad (12) 工質得到的有效熱能QU為: QU=qmcp(Ti-To) (13) 式中:Ti、To分別為集熱管工質進口、出口溫度,K;qm為工質的設計質量流量,kg/s;cp為工質在平均溫度下的比定壓熱容,kJ/(kg·K)。 在穩態情況下,考慮集熱器的熱轉移因子,能量平衡方程為: QU=FR(Qsun-QL) (14) 式中:FR為熱轉移因子;F′為效率因子;UL為熱損失系數。 直通式真空集熱管的瞬時熱效率η為: (15) 式中:AP為直通式真空集熱管有效采光面積,m2。 工質的進出口溫差ΔT為: (16) 采用MATLAB軟件編制計算程序,通過假定溫度法迭代求解,首先輸入集熱管結構、物理及氣象參數,取玻璃內管外壁溫度T3,然后假設T5=T6,計算是否滿足|Q34rad+Q34cond-Q56conv-Q56rad|≤δ(δ為設置的計算誤差),如果滿足,則假定合理;如果不滿足,令T5=T6+ΔTb(ΔTb為溫度步長),繼續迭代計算,直到滿足條件為止。一維傳熱模擬計算流程見圖2。 圖2 模擬計算流程 影響集熱器熱性能的因素分為氣象參數(太陽直射輻射強度、環境溫度和風速等)和運行參數(工質流量和進口溫度等),筆者用瞬時熱效率和工質的進出口溫差來表征集熱器的熱性能。 瞬時熱效率隨環境溫度和風速的變化見圖3,瞬時熱效率隨太陽直射輻射強度和工質進口溫度的變化見圖4。 圖3 瞬時熱效率隨環境溫度及風速的變化 圖4 瞬時熱效率隨工質進口溫度及直射輻射強度的變化 由圖3可知:集熱器瞬時熱效率隨環境溫度升高而增加,隨風速增加而減少;在較高溫度時,瞬時熱效率受風速影響減小,在較高風速時,環境溫度對瞬時熱效率影響較大;風速為0 m/s時,環境溫度對集熱器瞬時熱效率影響極小。由圖4可知:集熱器瞬時熱效率隨工質進口溫度升高而減小。當工質進口溫度等于環境溫度時,瞬時熱效率與直射輻射強度無關;當工質進口溫度大于環境溫度時,瞬時熱效率隨直射輻射強度的增大而減小;當工質進口溫度大于環境溫度時,瞬時熱效率隨直射輻射強度的增大而增大。 集熱器作為太陽能熱水系統熱源,研究其進出口溫差的變化極其重要,環境溫度和風速對集熱器進出口溫差的影響見圖5。 圖5 工質進出口溫差隨環境溫度及風速的變化 由圖5可知:集熱器工質進出口溫差隨著環境溫度的增加而增加,隨著風速的增加而減少,且在較高風速時,集熱器工質進出口溫差受環境影響較大,而在較高溫度下風速對進出口溫差影響變弱。 工質進出口溫差和太陽直射輻射強度對集熱器進出口溫差的影響見圖6。圖7為集熱器進出口溫差隨工質質量流量和直射輻射強度的變化。 圖6 工質進出口溫差隨工質質量進口溫度及直射輻射強度的變化 圖7 工質進出口溫差隨工質流量和直射輻射強度的變化 由圖6可知:集熱器工質進出口溫差隨工質進口溫度增加略微減小,隨直射輻射強度增加而有較大增加。由圖7可知:集熱器工質進出口溫差隨工質流量增加而減小,且有逐漸趨于平緩趨勢,在較大流量時,直射輻射強度對進出口溫差影響變小。 采用太陽能集熱器熱性能室外動態測試方法[10-11],進行實地測試,將實驗結果與模擬結果進行比較分析,實驗平臺見圖8。 圖8 集熱管熱性能實驗現場 對實驗數據進行處理,得到不同氣象參數下集熱管工質進出口溫差。在所測的數據庫中選取在太陽直射輻射強度、環境溫度和風速等大致相同時的實驗數據,得到進出口溫差在一定的氣象條件下,隨工質質量流量的變化曲線,并與模擬結果進行對比分析,圖9為工質質量流量對直通式全玻璃真空集熱管進出口溫差的影響。 圖9 工質質量流量對進出口溫差的影響 由圖9可知:模擬結果與實驗結果基本吻合,誤差在15%以內,驗證了理論建模結果的可靠性。工質進出口溫差隨工質質量流量增加明顯減少,整體上實驗值略低于模擬值,這可能是由于實驗過程中未將部分熱損失計算在內。 采用準穩態的實驗方法,同時為保證2種集熱管(傳統式和直通式)外部條件一致,把2種集熱管放在同一支架同時進行實驗,另外控制兩邊流量計示數一致,同時記錄太陽直射輻射強度和溫度等數據,實驗平臺同圖8。 實驗中,體積流量取25 L/h,為保證系統整體處于準熱平衡狀態,先等待30 min再開始測量,每隔10 min記錄一組數據,得到2019年6月15日的數據見表2。 表2 記錄數據 真空集熱管瞬時熱效率隨時間變化圖見圖10。 圖10 兩種真空集熱管瞬時熱效率隨時間變化 由圖10可知:在環境參數和運行參數相同條件下,直通式集熱管的瞬時熱效率高于傳統式集熱管。由于工質進入集熱管時仍受到水壓作用,傳統式集熱管中工質流動方式并不是完全的自然對流,傳熱系數得到提高,瞬時熱效率也會有一定程度提升。 (1) 針對單根直通式全玻璃真空集熱管建立一維穩態傳熱模型,借助MATLAB軟件采用假設溫度法迭代求解,用瞬時熱效率、工質進出口溫差等參數表征其熱性能,得到變化曲線,并對計算結果進行分析,得到結論為:環境溫度、風速及太陽直射輻射強度對集熱器熱性能影響較大,應充分利用氣象參數提高集熱器熱性能;工質進口溫度越高,瞬時熱效率越低,而進出口溫差改變較小,隨工質流量增加,進出口溫差先下降最終趨于平緩,因此實際應用中應選取合適的運行參數,使集熱器熱性能最佳。 (2) 通過動態測試方法,模擬值與實測值的誤差在15%以內,驗證了模型的正確性,并以對比實驗證明了直通式全玻璃真空集熱管熱性能優于傳統式。1.3 玻璃內管外壁到玻璃外管內壁的輻射傳熱
1.4 玻璃內管外壁到玻璃外管內壁的對流傳熱
1.5 玻璃外管內壁到玻璃外管外壁的導熱傳熱
1.6 玻璃外管外壁到環境的對流傳熱
1.7 玻璃外管外壁到環境的輻射傳熱
1.8 熱損失、瞬時熱效率及工質進出口溫差
2 計算結果及分析
2.1 瞬時熱效率模擬分析
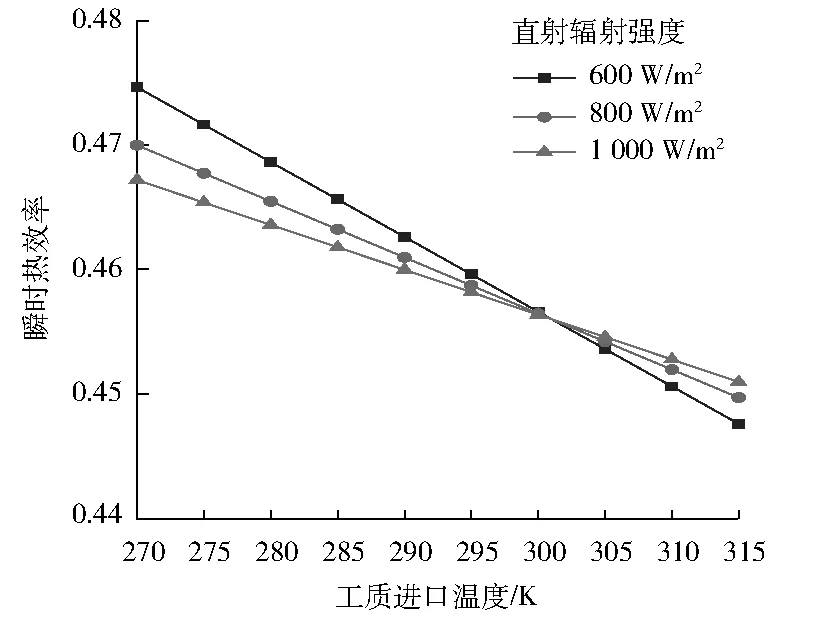
2.2 進出口溫差模擬分析
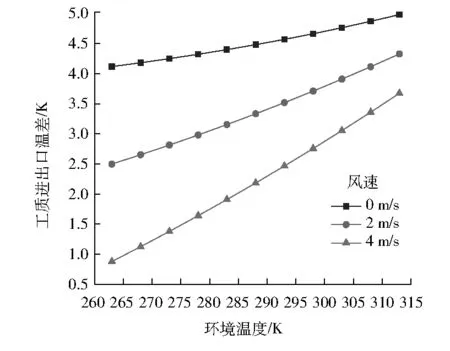
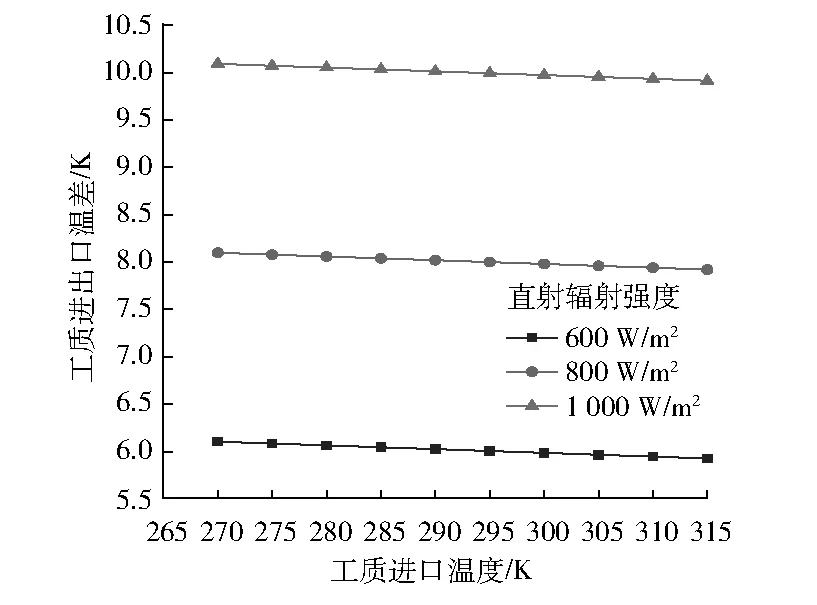
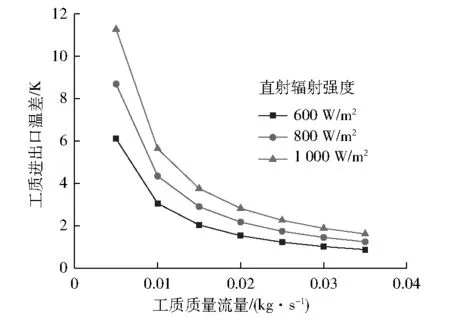
3 實驗分析驗證
3.1 模型驗證

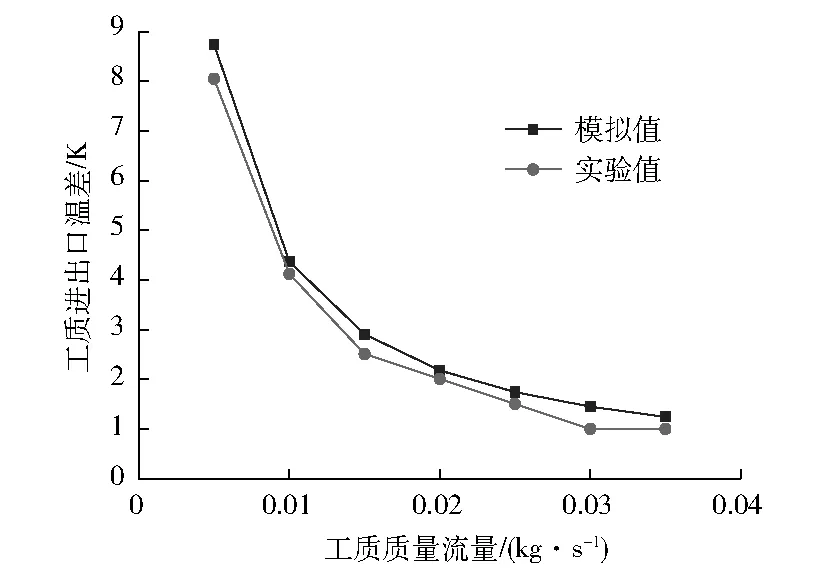
3.2 兩種集熱管熱性能實驗對比
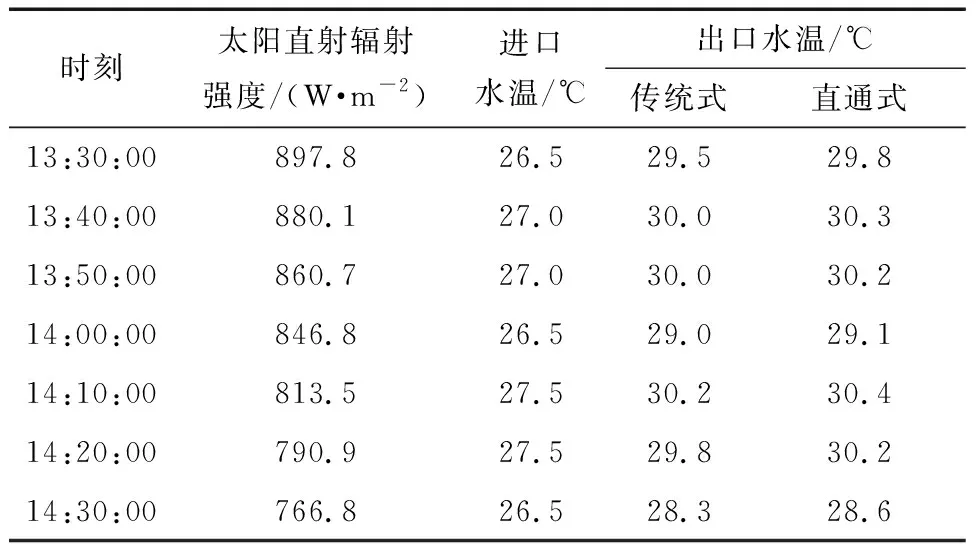

4 結語

