基于節點配置策略的有分流換熱網絡優化性能探析

徐玥，崔國民

（上海理工大學新能源科學與工程研究所，上海市動力工程多相流動與傳熱重點實驗室，上海 200093）

換熱網絡優化問題是化工領域研究最廣泛的問題之一，其通過熱、冷流股之間的合理匹配，可實現系統能耗的減少和經濟效益的提升。為此，在設計階段構造高效、靈活、編譯簡單的優化模型可成為輔助換熱網絡問題發展的重要突破。

Yee 和Grossmann[1]提出的分級超結構模型（stage-wise superstructure model，SWS）是典型的結構化模型，在模型的每一級內可完成冷、熱流股的全匹配，并通過多級設置擴增其求解域。但其對于SWS 模型有諸多限制，如將公用工程置于流股末端；熱、冷流股上分支數目需等于冷、熱流股的流股數目；為簡化模型計算，采用等溫混合的方式；禁止分支上連接多個換熱器以及旁流結構等，使得SWS 模型的能力受到一定的限制。為提高求解質量，針對SWS 模型的改進方法可分為以下幾類：將公用工程作為流體參與換熱[2]以增加匹配的多樣性；在分流結構中添加公用工程，提升結構變異的能力[3-5]；引入多種公用工程[6-7]，在實現網絡能量平衡的基礎上，減少年綜合費用。此外，Liao等[8-10]在原轉運模型的基礎上，增加了分流、旁流、環流等結構，并引入了傳質過程，該模型有效提升了優化質量。雖然以上針對結構化模型的方法均促進了優化結果的提升，但同時增加了網絡中的優化變量，其固定的匹配模式在優化中引入大量無效分流結構，對尋求優質結果形成阻礙，盡管一些改進策略可提升算法搜索能力，但也相應增加了算法的復雜度，降低了優化效率[11-13]。

為打破模型的模式化匹配對優化進程造成的影響，肖媛[14]、Xu 等[15]提出了節點非結構模型（nodes-based non-structural model，NNM）。NNM模型的設定相對自由、靈活，換熱器的生成可表示為任意兩個空置節點的連接，與結構化模型相比，NNM 模型可在有限節點的設定下為算法提供更多的潛在結構。此外，在有分流NNM 模型中，換熱器串聯數目、分流數不受算例流股數目的限制，可根據經驗自行設定，減少了無效變量的引入，提高了求解效率[15]。

在分析NNM 模型優化過程及結果時可發現：NNM 的模型參數設定依然采取統一的方式，即NNM 模型中所有熱流股共用一組模型參數，冷流股共用一組模型參數。因此，為使模型得到更優的結果，在設定流股的分流數時，需分別滿足熱、冷流股中分流最多的需求。從算例的流股參數及大量優化結構配置的分析中可知，不同流股對于分流的需求不同，同一類型的流股共用一組節點參數會造成部分分流的浪費，影響優化效率。為實現各流股的個性化匹配需求，提高網絡中分流結構的利用率，本文提出了節點配置策略。該策略可根據各流股性質調節分支數和分流組數，在網絡節點數一定的前提下，通過對節點的合理化配置，促使有效結構的生成，引導算法尋得更優結果。

1 數學模型及優化算法

1.1 節點非結構模型

節點非結構模型（NNM）是新型的換熱網絡優化非結構模型。在NNM 模型中，換熱器的位置通過網絡中設置的節點位置量化標定，流股上的分支數、分流組數以及串聯結構中的節點數均可根據算例的規模及其優化難度自行設置。

NNM 模型中節點配置設定如下：NfH，nfH=1,2,…, NfH表示熱流股上的分流數；NfC，nfC=1,2,…,NfC表示冷流股上的分流數；MbH，mbH=1,2,…,MbH表示熱流股分支上串聯的節點數目；同理，MbC，mbC=1,2,…,MbC表示冷流股分支上的串聯節點數目；熱、冷流股上分流組數分別用NdH，ndH=1,2,…,NdH和NdC，ndC=1,2,…,NdC表示。基于以上設定，單股熱流股上的節點數目NeNH和單股冷流股上的節點數目NeNC計算如式(1)、式(2)所示，熱、冷流股上總節點數NtH和NtC計算如式(3)、式(4)所示，熱、冷流股上總分流數NSPH和NSPC計算如(5)、式(6)所示。

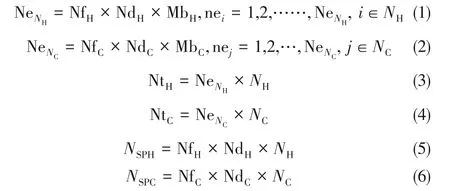
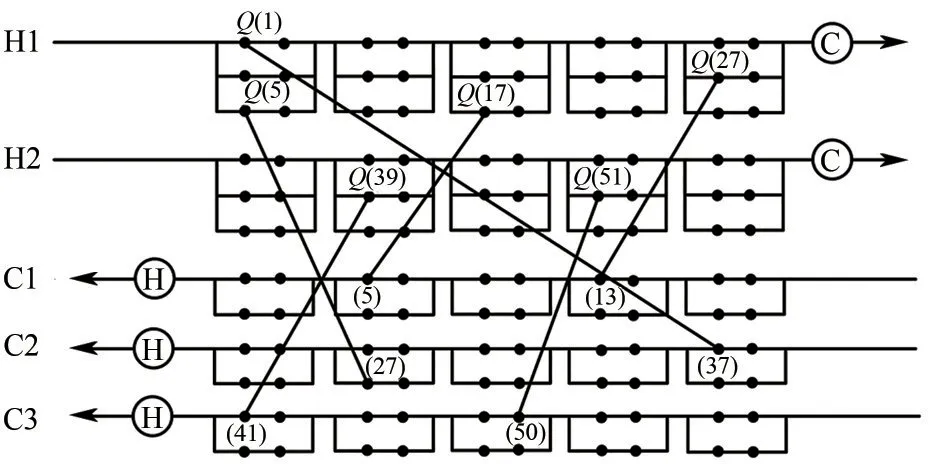
圖1 NNM模型結構

以小規模算例H2C3為例，將NNM模型結構圖繪制如圖1所示。其中節點參數的設置如下NfH=3，NfC=2，MbH=MbC=2，NdH=NdC=5。圖中給出了6 個換熱器的匹配方式，換熱器的位置可用節點的序號進行標定，圖1中以括號內數字表示。

1.2 目標函數

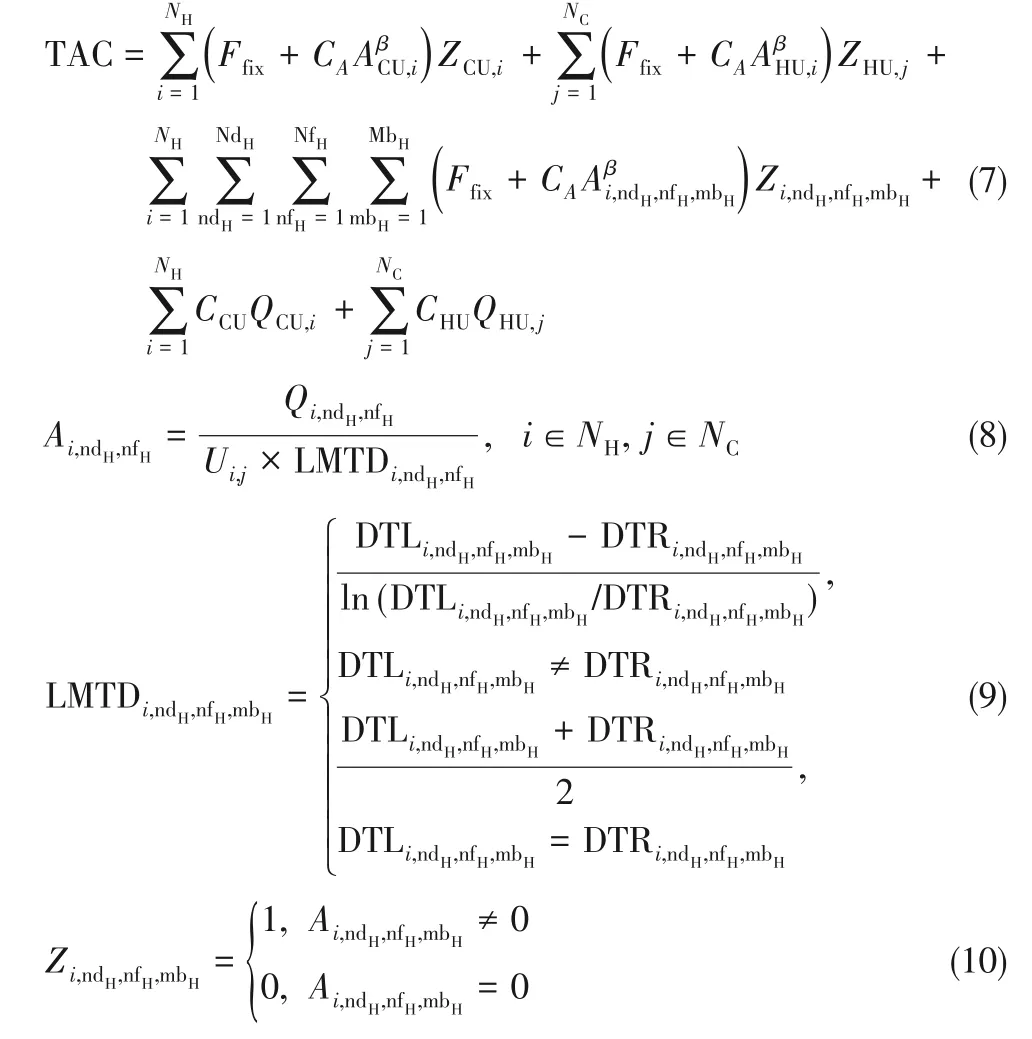
換熱網絡優化問題的目標函數為年綜合費用（total annual cost，TAC），根據模型設定，TAC 的計算式如式(7)所示。年綜合費用由投資費用和運行費用組成，式(7)前3項分別為冷公用工程、熱公用工程及換熱器的投資費用，其中A為面積，Q為換熱量，Ffix、CA、β分別表示投資費用中的固定投資費用、面積費用系數以及面積費用指數；后兩項為冷公用工程和熱公用工程的運行費用，CCU、CHU為冷、熱公用工程的單位費用系數；Z為二元變量，表示所處位置是否有換熱器，當換熱器存在時Z=1，否則為0，其中換熱器的面積以式(8)、式(9)計算，其中LMTD 為對數平均溫差，DTL、DTR 表示節點左、右兩端的溫差，Z的取值規則如式(10)所示。

1.3 約束條件

（1）流股上的熱平衡［式(11)、式(12)］

（3）冷、熱公用工程熱平衡［式(15)、式(16)］

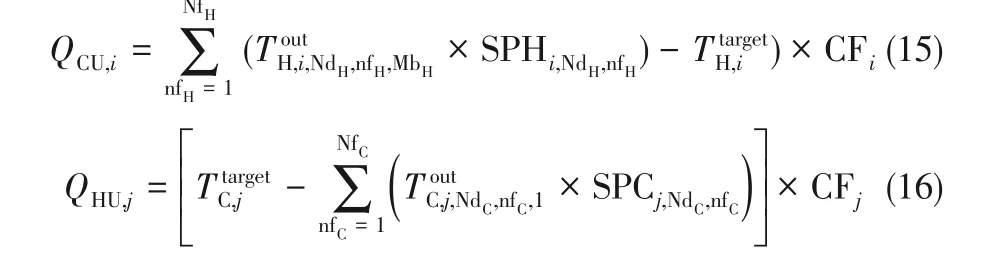
（4）冷、熱分流比相關約束［式(17)、式(18)］

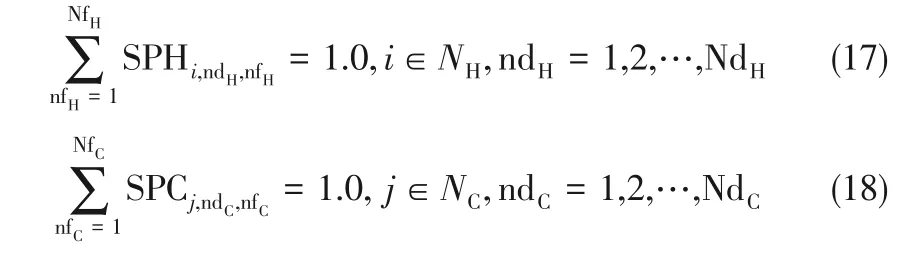
（5）溫度可行性約束及溫差約束 網絡中的溫度約束可保障熱流股的溫度從入口溫度到目標溫度遞減，冷流股的溫度從入口溫度到目標溫度遞增，具體如式(19)～式(23)所示，其中涵蓋了換熱單元面積及換熱量的非負約束。

1.4 強制進化隨機游走算法

文中采用的算法為強制進化隨機游走算法[16]（random walk algorithm with compulsive evolution，RWCE）。該算法通過調節換熱器的換熱量實現網絡中整型變量和連續型變量的同步優化。同時，以一定的概率（δ）接受差解，提高了算法全局尋優的能力。RWCE算法是目前相對高效的啟發式算法之一，算法具體流程如圖2所示。

2 NNM 模型中節點參數對優化結果的影響分析

采用NNM 模型優化換熱網絡時，有效的分流可促進優質結構的產生，而無效的分流則會制約結構變異，對搜索全局最優值造成障礙，因此分流的設置直接影響結果的優劣。在分析大量算例的網絡結構中分流所在流股及數目時發現：①分流結構在熱容流率較大的流股上出現的頻率較高，可多次利用其溫度對不同流股進行換熱；此外，熱容流率相近的流股易于匹配，利用分流對熱容流率較大的流股進行處理后，可增加該流股與其他流股匹配的概率，促進結構中整型變量的變異，提升算例優化質量的提升。②不同流股對于分流的需求不同。網絡中存在一部分流股，無論初始分流如何設置，流股上始終無法生成分流或其分流常使算法停滯于局部極值。

在NNM 模型的設定中，熱、冷流股各采用一組節點參數，這導致節點參數的設置既要滿足所有流股對分流的生成需求，又要保障算法不會因網絡中節點數目過多難以跳出局部極值。因此，節點參數的配置問題仍需進一步討論。以10SP算例為例，其來源于Ahmad[17]，參數見表1。

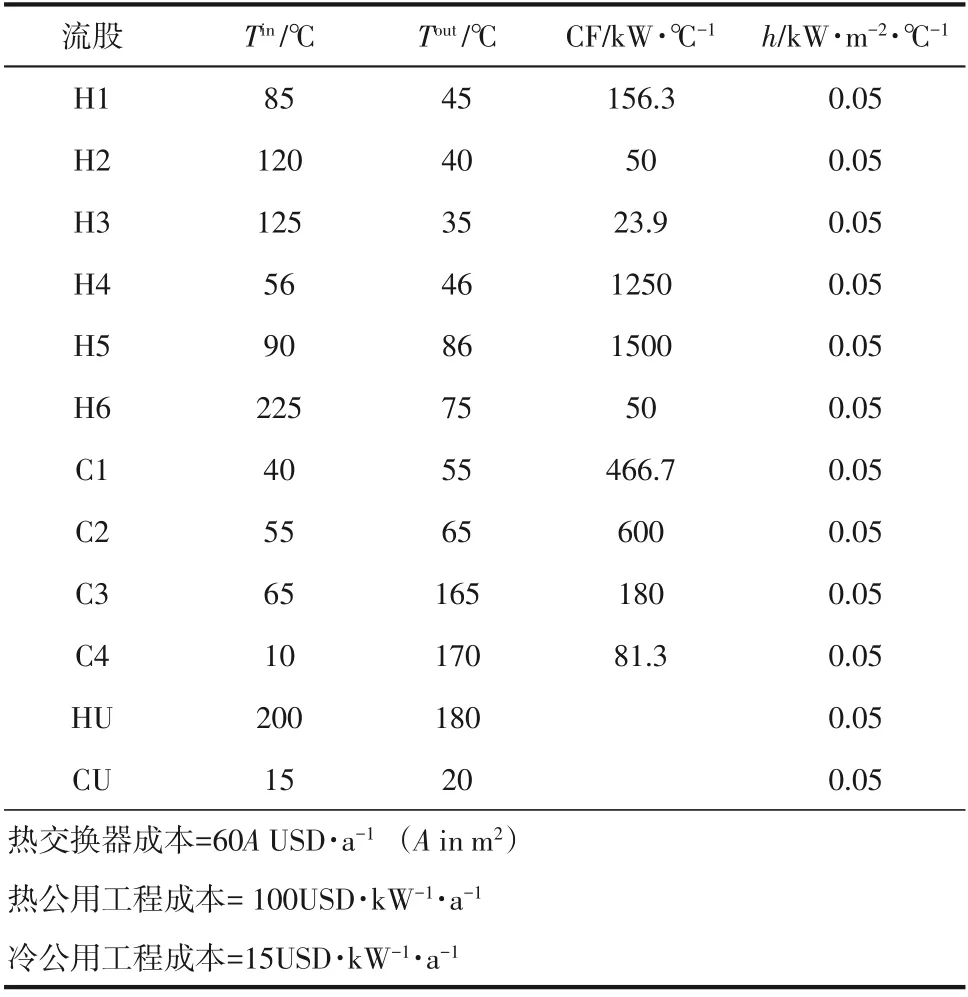
表1 10SP 算例參數

表1給出了各流股熱容流率，從數據的對比可知，熱流股中熱容流率最大值和最小值相差62.8倍；冷流股中熱容流率相差5.74倍。為證實節點參數對算例結果的影響，表2給出了5組不同初始節點參數設定下8000 萬次迭代后的結果對比。其中測試組A 中NeNH=NeNC=30，測試組B 中NeNH=NeNC=24，R-NfH和R-NfC分別表示優化結果中熱、冷流股上出現分流的次數。

從表2中數據可知如下結果。

（1）在網絡節點總數相同時，不同的節點參數對結果影響較大，其中A組中最好和最差的結果相差1957USD/a，B組中結果相差1219USD/a。

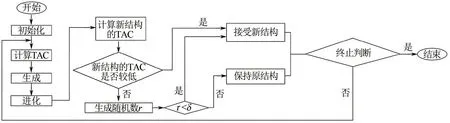
圖2 RWCE算法流程

表2 不同節點參數下10SP算例的結果

（2）所有測試結果中的分流均在冷流股上生成，且分流數及所在流股隨節點參數的不同有所變化，這表明網絡中節點的配置關系影響結果中分流的次數。從A組數據可知，在總節點一定時，增加冷、熱流股的分流支數時，網絡中易生成分流，但不合理的分流會造成結果陷入局部極值無法脫離。

（3）10SP算例在測試中主要在C1、C2、C4上生成分流，且所有結果在C1流股上均生成了分流，這表明在C1 流股上保留較多的分流結構有利于獲取更優的結果；對比B2 和B3 可發現，減少C4 流股上的分流可使得結果降低586USD/a，表明限制C4 流股上分流結構的生成，可減少局部極值結構的生成阻礙算法獲取更優結果。

（4）測試組中C2 流股上生成分流導致優化停滯于局部極值中，但文獻較優結果[18-19]的結構均在C2 上生成分流，其原因為RWCE 中參數的設置影響到對潛在結構的取舍[20]。綜合較優文獻中10SP結果，在參數合理的前提下，C2 上保留其分流能力可促進算法獲取更優的結構。

根據以上幾點分析，NNM 模型中節點數一定時，合理調控流股上分支數和分流組數，可推動優化結果的提升，但同屬性流股上采用一組節點參數時，卻很難協調不同流股對分流的需求。由于采用RWCE算法優化時，優化結果是多參數組合后的共同作用，因此適用于該算例的節點配置不一定適用于其他算例。基于以上原因，雖然本文無法給出具體的影響規律，但以上分析為后續節點配置策略的提出提供了思路和依據：①應根據算例特點合理地配置流股的分支數，過多的分支設定會使得算法陷入局部極值；②原NNM 模型的節點參數配置為定式配置，而在網絡的總節點相同時，不同的節點配置方式對結果有一定的影響，但原模型的參數設定很難同時滿足有所流股的分流需求，因此優化質量較差或優化效率較慢。基于此，應根據流股參數對其進行導向性的配置，提高網絡中節點的利用率，輔助算法避開無效結構對優化造成的阻礙，快速得到潛在的優勢結構，提升算法的優化質量和優化效率。

3 節點配置策略

基于NNM 模型的特點，提出了節點配置策略（nodes' adjustment strategy）。該策略可根據算例中各流股的熱容流率，調控其在模型結構中的分支數和分流組數，使得熱容流率較大的流股保留較多的分支數，而熱容流率較小的流股上產生較多的分組數。選擇的函數應該滿足以下幾點：①流股的分支數應隨著熱容流率的增加保持單調遞增的關系；②在兩股流股的熱容流率較大時，熱容流率較小的流股上應盡量保留一定的分流，熱容流率相近的流股，其分流數也應相近。根據上述要求，本文采用三角函數調控容流率和分支數之間的關系，具體表達如式(24)～式(27)所示，式中CFH,MAX、CFC,MAX為熱、冷流股上熱容流率的最大值，CFH(i)和CFC(j)為第i股熱流股和第j股冷流股的熱容流率；α為隨機數，用于調控各流股的分支數，NFH及NFC分別為熱、冷流股的初始設定值。式(24)和式(26)為熱、冷流股分支數的調節方式，式(25)和式(27)為對應流股分流組數的調節方式。經該策略的調整，該策略依據流股的熱容流率進行個性化的節點布置，為算法獲取更優質的結構提供了導向性輔助。

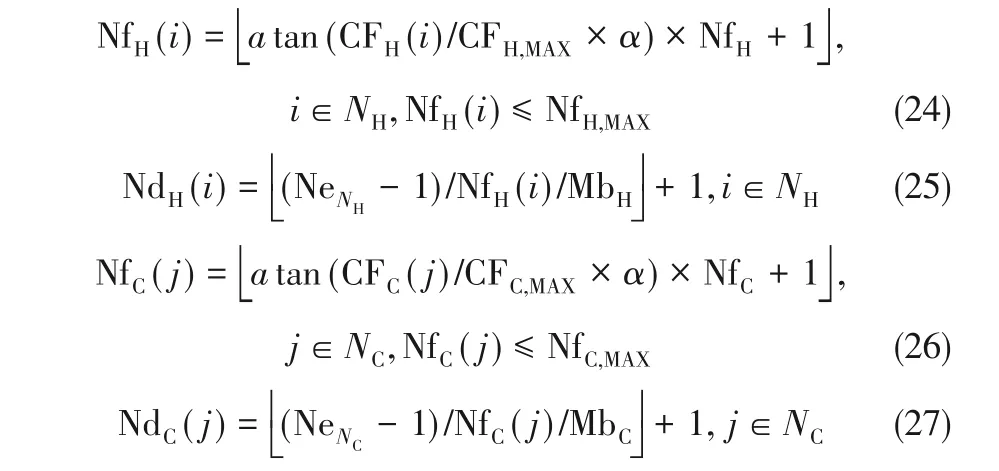
圖3 給出了加入節點配置策略的NNM 模型（nodes-based non-structural model with adjustment strategy，NNM-AS）調節流股節點配置的示意圖。以分支單節點的NNM 模型為例，由圖中可知，經節點配置策略調整后節點可依據流股屬性調控，且調整后的流股上可兼備有分流和無分流兩種節點配置，保障流股分流能力的同時調整了求解域。

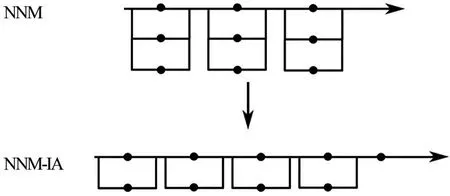
圖3 應用NNM-AS調節流股節點過程

4 算例分析

4.1 10SP算例

采用NNM-AS 模型處理后，10SP 各流股節點配置見表3，初始節點參數為NdH=NdC=10，NfH=NfC=3，MbH=MbC=1。根據流股熱容流率，熱流股中H4、H5 上分流支數為3，其余流股均為無分流流股；冷流股中C1、C2 上分流支數為3，其余流股上分流支數也受到一定的限制。

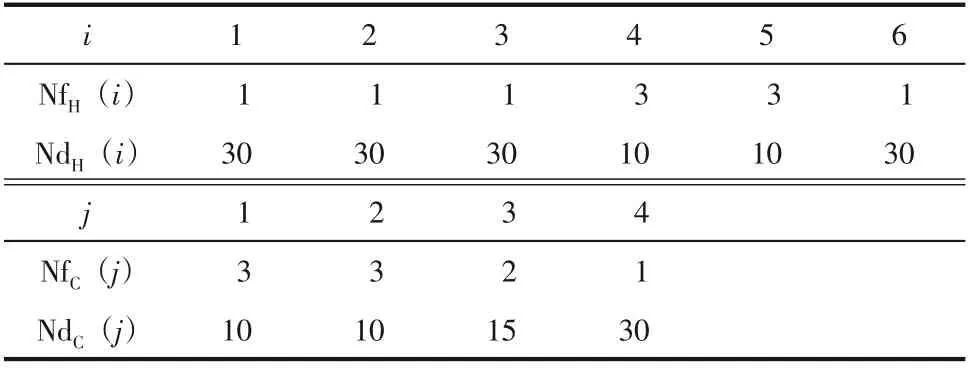
表3 NNM-AS模型中10SP算例各流股節點配置

在此節點配置下，優化可得10SP 結果如圖4所示，節點處括號內數字為該節點的出口溫度，TAC=5585292USD/a，較目前文獻中最優費用低340USD/a，結果對比見表4。從結構對比看，圖4中結構相較其他文獻中結構已產生較大的改變，換熱單元數目也大幅度提升。因10SP 中不含固定投資費用，網絡中換熱量之間的制約限制結構變異，通過改進后的策略進行優化，可打破原有設置的限制突破局部極值。由表3可知，H4、H5、C1、C2、C3以有分流模式參與優化，而H1、H2、H3、H4、C4 以無分流模式參與優化。NNM-AS 模型兼顧了分流和無分流兩種模型，由此可獲得更多的潛在優勢結構。

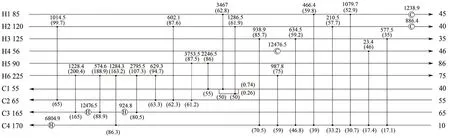
圖4 采用NNM-AS優化10SP算例結果（TAC=5585292USD·a-1）

在相同參數設置下，分別采用NNM-AS 模型與NNM 模型用于RWCE 算法優化10SP，探究改進后模型對優化效率的提升效果，其TAC 隨迭代次數變化如圖5所示。

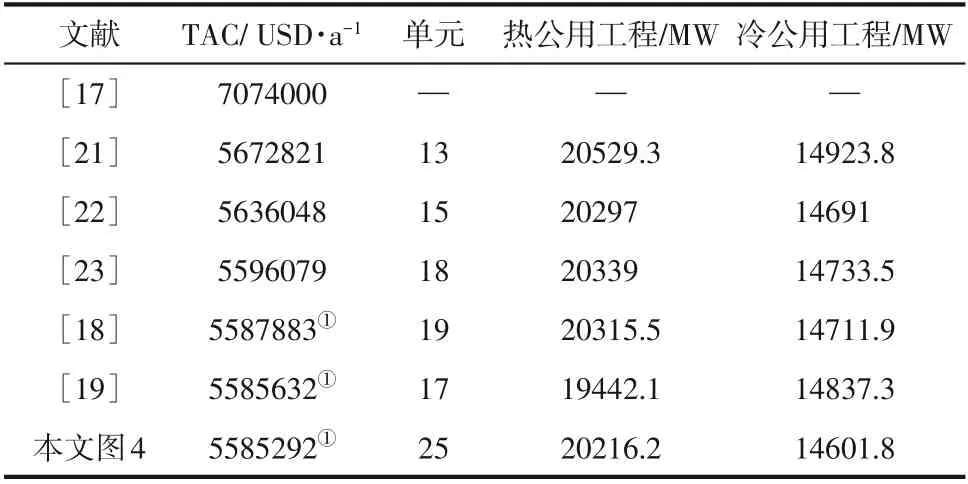
表4 10SP算例結果對比

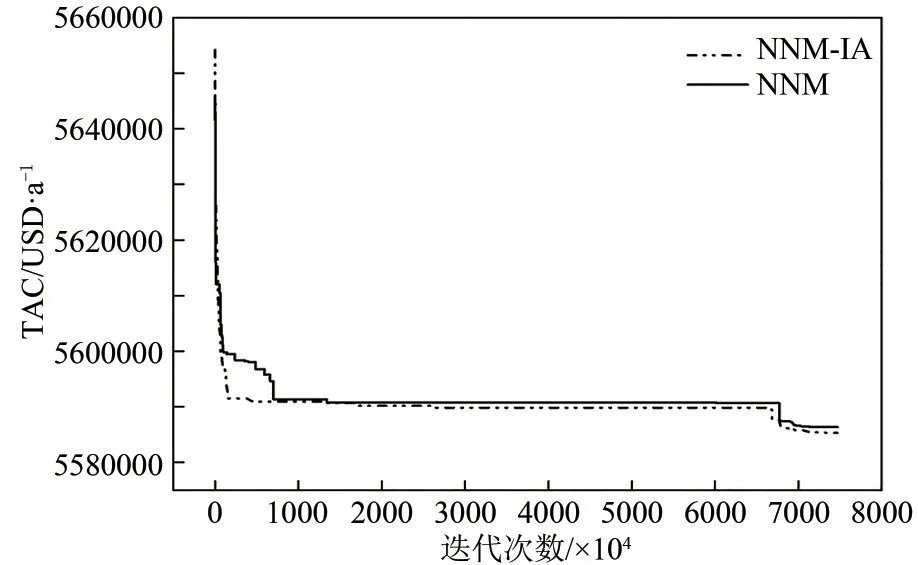
圖5 NNM-AS和NNM模型優化10SP算例結果對比

從TAC 曲線變化可知，在對網絡中節點進行導向性配置后，抑制了網絡中無效的分流結構，使得算法在優化初期便可找到較優的結構，并在整個優化過程中始終處于優勢地位，在7500 萬次迭代中獲得TAC=5585292USD/a，而此時以NNM作為優化模型獲得的TAC=5586224USD/a。由此可知，NNM-AS模型可有效輔助算法提升效率。

4.2 15SP算例

算例來源于Bj?rk等[24]，流股參數見表5。由于優化算法的貪婪性，8000USD/a的固定投資費用會對換熱器的生成和消去形成阻礙，增加網絡中整型變量變異的難度。因此，在不改變問題節點數的前提下，根據流股的熱容流率對其進行智能化調整，可有效避免一些無效的配置，從根本上減緩差解結構對優化進程的阻礙程度，減少算法在排除較差結果過程中浪費的計算時間，實現優化結果和效率的雙重提升。

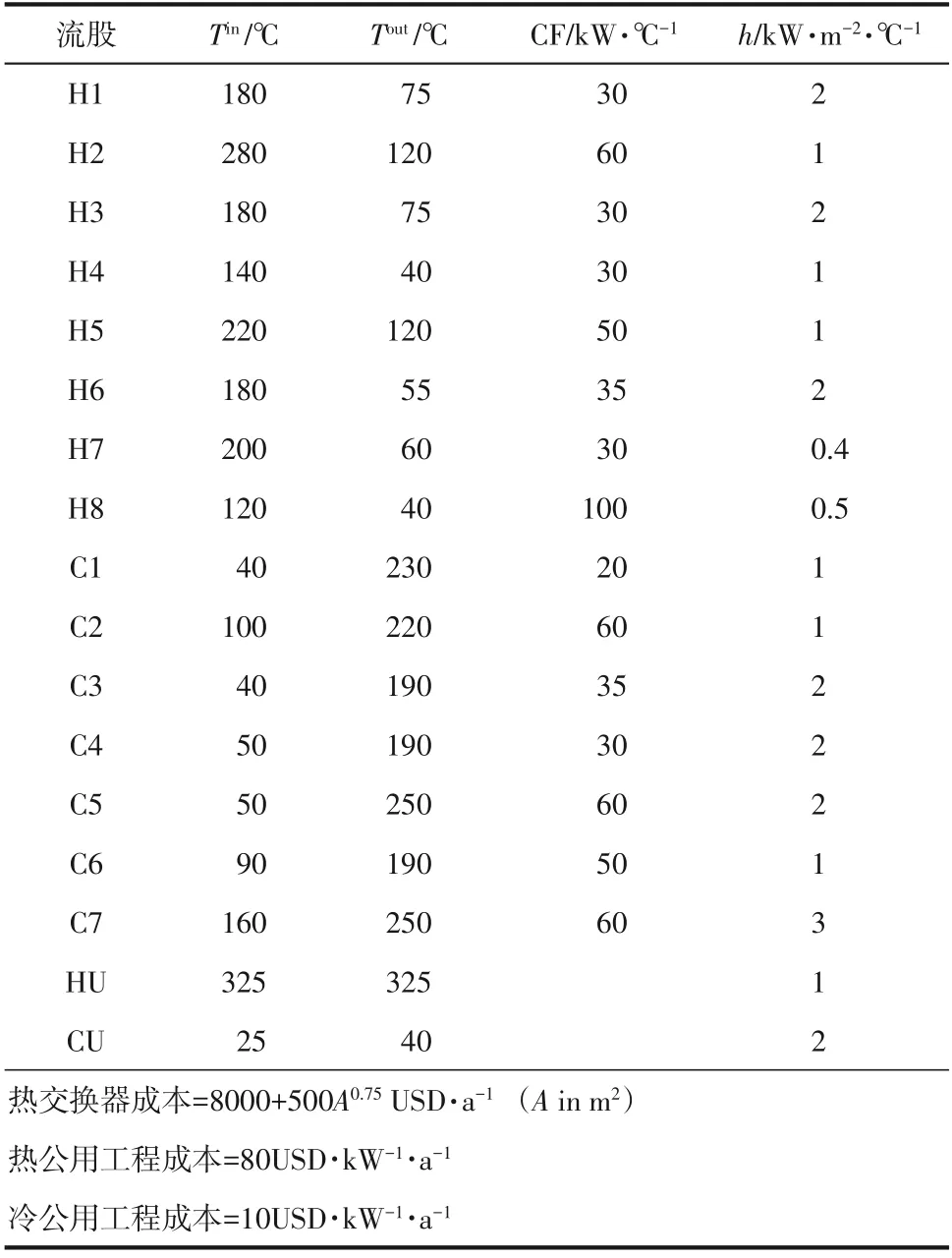
表5 15SP算例參數

NNM-AS 模型優化15SP 算例時，節點參數為NdH=5，NfH=3，NdC=4，NfC=4，MbH=MbC=2。經調整各流股的分流組數和分支數見表6。從表6 中數據可以得知H1、H3、H4、H5、H6、H7、C3、C4上出現了有分流和無分流兩種配置關系，這種在同一股流股上實現兩種模式的配置打破了有分流模型中對于結構的定式配置，更突顯了NNM 模型“非結構”的特性。

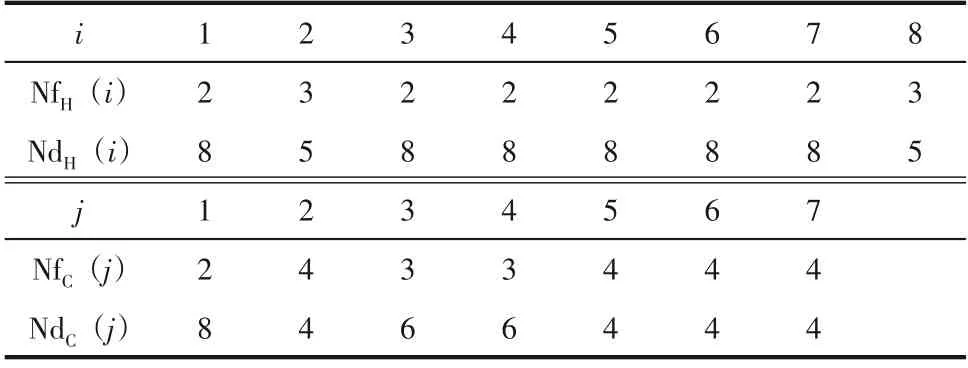
表6 NNM-AS模型中15SP算例各流股節點配置

應用RWCE 算法和NNM-AS 模型優化15SP 算例得到的費用及結構如圖6所示。

圖6 中TAC=1492628USD/a，根據表7 中結果對比，圖6 中結果較目前文獻中最優結果低2285USD/a。與徐玥等[31]的結果對比可發現，圖6在H5C6上生成了一個換熱器，通過對部分換熱器換熱量的調節，使得C2、C3 流股上無需外加公用工程，因此換熱單元數相較文獻[31]少1 個，進而降低了費用。在同參數下相同迭代步數內，采用NNM 模型優化15SP 算例，結果為1514066USD/a，佐證了在網絡中多種節點配置對獲取較優結果的重要性。

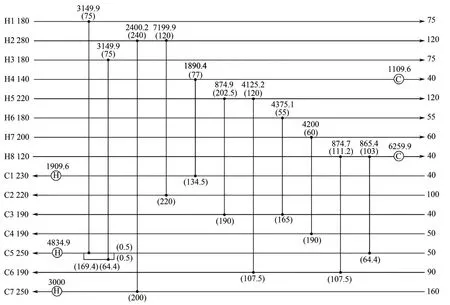
圖6 采用NNM-AS優化15SP算例結果（TAC=1492628USD·a-1）

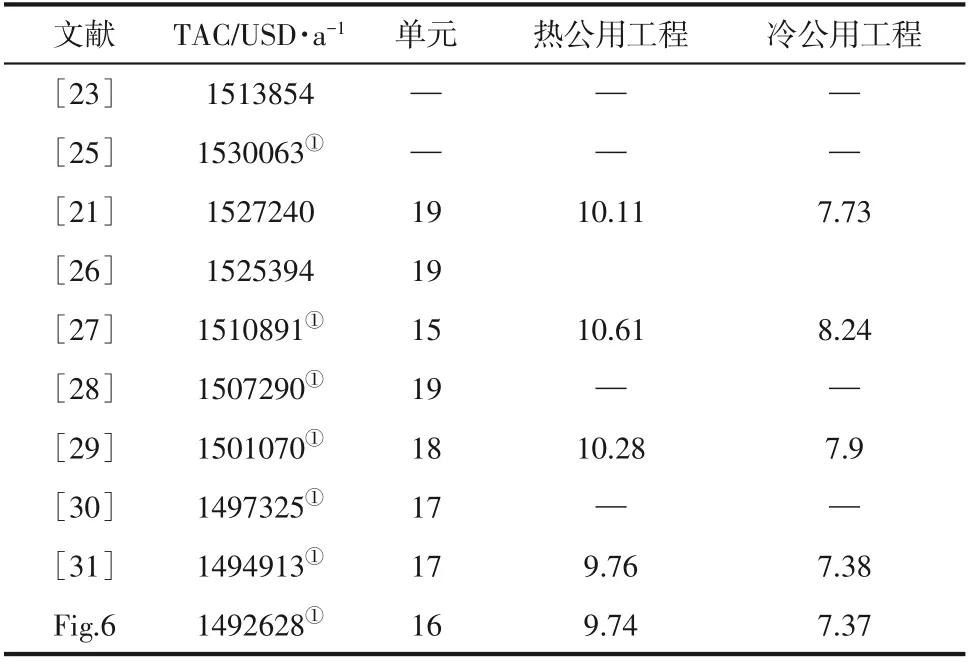
表7 15SP結果對比

5 結論

在分析NNM 模型的節點參數對網絡配置及優化結果的影響時發現，有分流網絡中不同流股對于分流的需求不同，且分流在熱容流率較大的流股上出現的概率較大，因此提出了節點配置策略用以提升NNM 模型優化能力。該策略可根據各流股的熱容流率調節其分流數與分流組數，使得熱容流率較大的流股上分流數較多而熱容流率較小的流股上分流組數較多。NNM-AS模型可對優勢結構的產生起到引導作用，減少了無效分流結構對優化進程的制約，縮短了獲取優質結果所需的時間。應用NNMAS模型和RWCE算法優化10SP和15SP算例，其結果分別比目前已有文獻中最優結果低340USD/a 和2285USD/a，且質量和效率均優于同參數下NNM與RWCE算法所得結果。

符號說明

A—— 換熱單元面積，m2

CA—— 面積費用系數，USD/(m2·a)

CF—— 熱容流率，kW/℃

CU—— 冷公用工程

Ffix—— 固定投資費用，USD/a

HU—— 熱公用工程

MbC—— 冷流股上分支上串聯節點數

MbH—— 熱流股上分支上串聯節點數

NC—— 冷流股數目

NeNC—— 單股冷流股上的節點總數

NeNH—— 單股熱流股上的節點總數

NdC—— 冷流股上的分流組數

NdH—— 熱流股上的分流組數

NfH—— 熱流股上的分流數

NfC—— 冷流股上的分流數

NH—— 熱流股數目

NSPC—— 冷流股上的分流總數

NSPH—— 熱流股上的分流總數

NtC—— 冷流股上的節點總數

NtH—— 熱流股上的節點總數

Q—— 換熱量，kW

R-NfH—— 優化結果中熱流股上分流次數

R-NfC—— 優化結果中冷流股上分流次數

SPC—— 冷流股分流比

SPH—— 熱流股分流比

T—— 溫度，℃

Tin—— 入口溫度，℃

Tout—— 出口溫度，℃

Ttarget—— 目標溫度，℃

TAC—— 年綜合費用，USD/a

Z—— 二維變量

δ—— RWCE算法中設置的接受差解概率