一類潛伏期傳染的SEIR模型穩定性分析


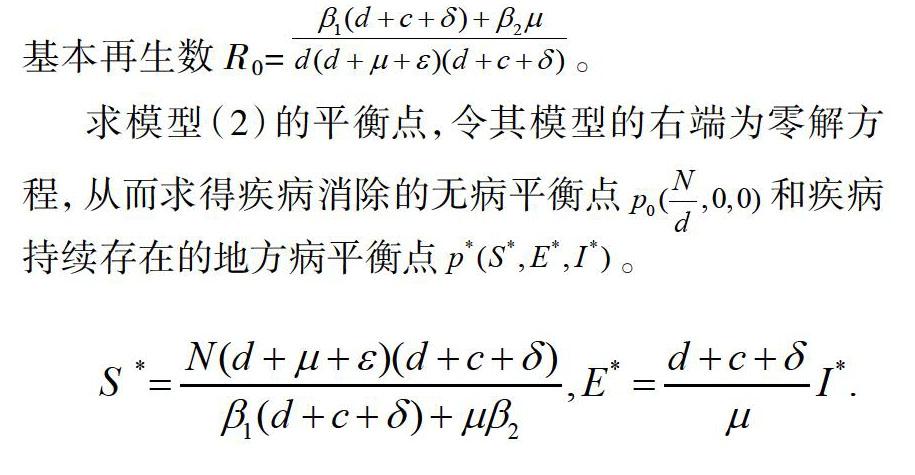
DOI:10.16661/j.cnki.1672-3791.2103-5042-3263
摘? 要:該文以一類具有標準發生率且潛伏期具有傳染性的SEIR傳染病模型為研究對象,首先通過計算得出決定疾病滅絕或持續存在的基本再生數、模型存在的無病平衡點和地方病平衡點,其次運用LaSalle不變集原理和構造適當的Lyapunov函數,證明當r0<1時,無病平衡點的局部和全局漸近穩定,此時流行病將會逐漸趨于滅絕而不會大規模爆發。
關鍵詞:基本再生數? 標準發生率? 潛伏期? Lyapunov函數? 全局漸近穩定
中圖分類號:O175.1? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼:A文章編號:1672-3791(2021)03(b)-0221-03
Stability Analysis of SEIR Model for a Class of Latent Infection
DOU Zhongli
(Chongqing Finance and Economics College, Chongqing, 401320? China)
Abstract: In this paper, we study a class of a standard incidence of SEIR epidemic model of the incubation period is contagious, first of all, calculated decision to extinction or persistent disease basic reproductive number of disease-free equilibrium and the endemic equilibrium model, then using the LaSalle invariant set principle and constructing suitable Lyapunov function, proved that, When ro<1, the local and global asymptotic stability of the disease-free equilibrium and the epidemic will gradually become extinct without large outbreaks.
Key Words: Basic regeneration number; Standard incidence rate; Incubation period; Lyapunov function; Globally asymptotic stability
在現實生活中,傳染病的廣泛存在對人類的生存和社會的發展構成很大的威脅。例如,蘇聯在1990年發生白喉流行病,波及東歐15個國家,死亡人數超過10萬;早在20世紀80年代初發現的艾滋病,已在全球奪取了2 500萬人的性命,死亡人數超過第一次世界大戰,現在仍然沒有任何藥物可以治療它。但是人類仍然積極在對抗這種免疫系統疾病,沒有喪失戰勝它的決心。2003年爆發的SARS病毒涉及到32個國家和地區,病死率達到11%;2015年持續蔓延的埃博拉病毒有9萬多人死亡,病死率高達50%和2020年初流行的新冠肺炎使全球超過20萬人死亡等,流行病時刻在威脅著人類的健康。
人類對于傳染病的傳染源、傳播途徑、發病原因、發病機理、傳播速度、流行規律的研究從未停止。傳染病在傳播過程中與人生活的環境有關,傳播過程中存在著“環境-人”與“人-人”兩種途徑。數學家們利用傳染病的傳播特點結合數學本身的理論知識研究傳染病的動力學性態,得到一些關于傳染病流行的更專業的理論結果,醫生利用這些理論結果解決傳染病的傳染問題。因此,利用動力學方法建立傳染病模型,分析流行病的發病原因、尋求防治策略、預測疾病的流行規律已成為重要的研究內容,是現在備受關注的熱點問題之一。
1? 模型建立
近幾十年來,傳染病動力學快速發展,由于傳染病傳播的不確定性和多樣性,關于傳染病問題的研究始終無法完美地解決,但是大部分傳染病問題都可以用數學模型來分析。關于傳染病生物數學模型[1],已經有很多專家和學者進行研究。例如:傳染病有“人-人”現象,專家給出隔離來切斷傳播途徑,并通過接種疫苗來預防傳染病的傳播。但是有一些傳染病具有一定的潛伏期,因此文獻[2-4]研究了一類具有潛伏期的傳染病模型,這類模型考慮了傳染病在染病期間具有傳染性,研究了模型的局部和全局穩定性,但是沒有考慮在潛伏期間也具有傳染性;文獻[5-8]研究了傳染病在潛伏期和染病期都具有傳染性,但是文中采用的雙線性發生率。當生存的環境中人數很多時,患病者與人數成正比的接觸率和實際的情況不太符合,因為在一定的單位時間內患病者所能接觸到易感者的數目是有限的;文獻[9]考慮了具有染病者康復的傳染病模型,但是文中只是在總人口數量不變的情況下進行討論,而人口數量是在發生變化的有一定的局限性。通常對于群居的人類和某些種群來說,標準發生率會比雙線性發生率更符合實際。因此,該文在上述文獻研究的基礎上,以一個更接近實際情況且復雜的標準發生率,研究在潛伏期和染病期均具有傳染性的傳染病模型。
式中,S(t)、E(t)、I(t)、R(t)分別表示t時刻易感者、潛伏者,染病者和恢復者人群數量:N表示總人口量,表示標準傳染率:d表示自然死亡率:μ表示潛伏者轉化為染病者的轉化率:ε、c表示潛伏者和染病者的恢復率:δ表示因病死亡率,參數d、μ、ε、c、δ為非負。由于模型(1)中前3個方程不含R,該文僅關心疾病是否流行,故可以不考慮模型(1)中的第四個方程,僅討論由前3個方程所構成的傳染病模型的動力學性態。由前面3個方程構成的平面系統為:
該文僅在正向不變集內,討論模型(2)的動力學性態。
2? 基本再生數和無病平衡點的穩定性
一個病人在平均患病期內所傳染的人數,稱為基本再生數[10-11]。基本再生數是用來區分疾病是否流行的閾值,當基本再生數比1小,即染病者在平均患病期間傳染的人數比1小,模型在正向不變集D內只存在著無病平衡點是全局漸近穩定的,疾病自然會逐步趨于滅絕;反之若基本再生數比1大,即染病者在平均患病期傳染的人數比1大,模型在D內還存在著地方病平衡點是穩定的,疾病將始終存在而逐漸形成一種地方病。該模型利用再生矩陣法計算可以得到模型(2)的基本再生數 R0=。
求模型(2)的平衡點,令其模型的右端為零解方程,從而求得疾病消除的無病平衡點和疾病持續存在的地方病平衡點。
引理:若線性化矩陣的所有特征值均具有負實部,則模型的解是漸進穩定的;若線性化矩陣的所有特征值均具有非正實部,或者其具有零實部的特征值僅有單重初等因子,則模型的解是穩定的;若線性化矩陣至少有一個正實部的特征值,或者有多重初等因子的零實部特征值,則系統的解是不穩定的[11]。
定理1:當時,模型(2)的無病平衡點是局部漸近穩定的[12-13];當時,模型(2)的無病平衡點是不穩定的。
證明:通過線性化得到模型(2)在無病平衡點處的Jacobi矩陣為:
因此得到特征方程為:
顯然,該模型有一個特征值λ1=-d<0,另外兩個特征值滿足方程,其中:
當時,有,,3個特征值的實部均小于零,由引理可知,模型(2)在無病平衡點處是局部漸近穩定的。
當時,有,有一個特征值實部大于零,由引理可知,模型(2)在無病平衡點是不穩定的。
定理2:當時,模型(2)的無病平衡點是全局漸近穩定的。
證明:構造適當的Lyapunov函數為[14]:
沿模型(2)軌線的全導數有:
當R0<1時,由Lasalle不變集原理可知,當時間趨于無窮時,模型的解均有染病者趨于零,易感者趨于N/d,而D中所有軌線均趨于無病平衡點,因此模型(2)的無病平衡點在D內是全局漸近穩定的。
3? 結語
該文討論了具有更接近實際生活的標準發生率的SEIR傳染病模型,利用再生矩陣法得到模型的基本再生數,求出模型的無病平衡點和地方病平衡點;利用LaSalle不變集原理和Lyapunov函數,證明當R0<1時,模型的無病平衡點的局部和全局漸近穩定性,這意味著,在生存的環境中無論開始感染的病人有多少,傳染病都不會大規模流行而是逐漸趨于滅絕。關于模型的地方病平衡點的局部和全局漸近穩定性有待于進一步解決。
參考文獻
[1] 馬知恩,周義倉,王穩地,等.傳染病動力學的數學建模與研究[M].北京:科學出版社,2004:33.
[2] 豆中麗,王銳.一類具有飽和發生率和潛伏期的SEIR模型的穩定性[J].中山大學學報:自然科學版,2019,58(2):155-160.
[3] 米曉麗.一類含潛伏期且總人口在變化的SEIRI傳染病模型的全局穩定性[J].山西師范大學學報:自然科學版,2015,29(1):15-18.
[4] 張改平,董玉才,許飛,等.具有垂直傳染且總人口在變化的SIRS傳染病模型的漸近分析[J].數學的實踐與認識,2011,41(18):139-143.
[5] 梁桂珍,郝林莉.一類潛伏期和染病期均傳染的SEIQR流行病模型的穩定性[J].西南師范大學學報:自然科學版,2020,45(3):1-9.
[6] 楊金根,王鐵英,張萍.潛伏期和染病期均傳染且具脈沖接種的傳染病模型[J].信陽師范學院學報:自然科學版,2017,30(3):345-348.
[7] 米曉麗,王鑫.一類潛伏期和染病期均傳染的SEIR傳染病模型的穩定性研究[J].山西師范大學學報:自然科學版,2016,30(3):12-14.
[8] 趙海全,王美娟,唐春婷.潛伏期和染病期均傳染的SEIS模型的分析[J].上海理工大學學報,2017,32(5):457-460.
[9] 方彬,楊金根,李學志.潛伏期和染病期均具有康復的年齡結構MSEIS流行病模型的穩定性[J].應用數學,2018,22(1):90-100.
[10] 馬知恩,周義倉,李承治.常微分方程定性與穩定性方法[M].北京:科學出版社,2015:6.
[11] Huang SZ. A new SEIR epidemic model applications to the theory of eradication and control of diseases and to the calculation[J].Mathematical Bioscienc-es,2008,2015(1):84-104.
[12] 郝林莉.幾類具有潛伏期的流行病模型的穩定性分析[D].鄭州大學,2019.
[13] 張瑞霞.基于動力系統的復雜社會網絡中傳播行為建模研究[D].山西大學,2018.
[14] Busenberg S,van den Driessche P. Analysis of a disease transmission model in a population with varying size[J].Journal of mathematical biology,2014,28(3):257-270.

