基于CNN擾動的極化碼譯碼算法

趙生妹 徐 鵬 張 南 孔令軍*

①(南京郵電大學通信與信息工程學院 南京 210003)

②(中國航天系統科學與工程研究院 北京 100048)

1 引言

極化碼是一種基于信道極化理論的信道編碼[1]，自Arikan提出以來，引起了廣泛的關注[2]，串行抵消(Successive Cancellation, SC)譯碼算法是Arikan針對極化碼的結構提出的極化碼獨有的譯碼算法，在SC 算法下，通過嚴格的數學證明，得到極化碼可以在二進制離散無記憶信道(Binary Discrete Memoryless Channel, B-DMC)下進行無差錯傳輸，并且容量可達[3]，與此同時，SC譯碼算法具有較低的計算復雜度，僅為O(Nlog2N)。然而在實際狀況下，碼長不可能“足夠長”，一旦發生錯誤的比特判決(比特錯誤)，由于順序譯碼的特性，錯誤的比特沒有機會被糾正[4]。

因此，基于SC譯碼算法的改進算法成為極化碼譯碼的研究熱點，研究者提出了一系列算法來改善極化碼的SC譯碼性能[5]。文獻[6]提出了SC翻轉(SCF)譯碼，在SC解碼失敗(通過CRC校驗檢測)，則嘗試識別并翻轉先前譯碼期間發生的第1位錯誤，一直嘗試直到譯碼通過CRC校驗，或達到最大嘗試次數。在文獻[7]中，針對SC譯碼只保留一條譯碼路徑，從而導致正確路徑容易丟失的問題，提出了串行抵消列表(Successive Cancellation List,SCL)譯碼算法，其可保留L條路徑。盡管SCL譯碼具有優越的性能，但是由于保留了L條路徑使其計算復雜度高、內存需求大、譯碼吞吐量低。因此，文獻[8]提出了簡化的SCL譯碼算法(Simplified SCL, SSCL)和快速簡化的SCL譯碼算法(Fast Simplified SCL, Fast-SSCL)，雖然它們都能降低計算復雜度，但是性能將有所下降。基于CRC輔助SCL譯碼算法(CA-SCL)[9]改進的自適應SCL譯碼算法(ADaptive SCL, AD-SCL)[10,11]，則根據譯碼序列的CRC校驗結果判斷是否增大L值重新譯碼，降低了整體譯碼復雜度同時獲得較好的譯碼性能，但是在低SNR時重譯次數較高。文獻[12]提出一種基于分段CRC的自適應SCL譯碼算法(Segmented-CRC ADaptive SCL, SCAD-SCL)，文獻[13]提出了多級CRC輔助校驗的SCL譯碼算法，降低了平均復雜度和時延。

針對極化碼SC譯碼算法性能不佳，且現有性能較好的SCL等改進譯碼算法復雜度較高的現狀，本文從SC配置的次優性和極化碼的最小距離[14]進行分析，通過向接收信號添加次級獨立隨機噪聲以改善極化碼譯碼器的性能[15]。傳統的SC譯碼算法通常僅提供一個輸出，如果該輸出被證明是無效的碼字，則聲明譯碼錯誤。然而，利用擾動算法，可以通過向接收信號添加次級獨立噪聲來產生其他可能的候選碼字。最近深度學習在處理噪聲等任務中取得了巨大的進步[16]，因此，本文通過CNN來對接收信號提取噪聲特征，根據接收信號在碼空間中與有效碼字的偏離程度，動態調節擾動噪聲的大小(噪聲方差)，對添加了擾動噪聲的接收信號重新計算似然信息并譯碼，設計迭代算法，重復該過程直到獲得有效的碼字或者達到迭代閾值。在復雜度較低的情況下，可提升誤碼率(Bit Error Ratio, BER)性能。

2 極化碼基本原理

由極化碼的編碼過程可知，極化碼的構造就是容量趨于1的比特信道(又稱為極化信道)的選擇過程，是以最優化SC譯碼性能為標準的，根據極化信道轉移概率函數式，各個極化信道具有確定的依賴關系：信道序號大的極化信道依賴于所有比其序號小的極化信道。基于這種關系，SC譯碼對比特進行判決時，需要假設之前得到的譯碼結果都是正確的，正是在這種情況下，極化碼被證明了是信道容量可達的。因此對于極化碼而言，基于SC的譯碼算法是最合適的，只有這樣才可以充分利用極化碼的結構，保證在足夠碼長時容量可達。

3 基于CNN擾動的極化碼譯碼算法

3.1 擾動噪聲譯碼

在實際通信系統中，噪聲是最不期望存在的，因為信道中的噪聲會對發送信息產生影響，嚴重時可造成有效信息在接收機處不能恢復，嚴重影響通信系統的性能。然而，從譯碼糾錯空間的角度分析，特定的擾動噪聲可能會有助于譯碼，進而提升了譯碼器的性能。圖1為基于碼空間的線性碼糾錯譯碼示意圖，其中M個碼字的可糾錯區域分別標記為a1, a2, ···, am。若以可糾錯區域a2為例，當發送與其對應的碼字c2時，接收信號y由于在信道中受到噪聲的干擾，落在譯碼空間中位置可能是隨機的。如果錯誤在可糾正范圍內，則其應將落在a2區域內，則根據譯碼規則可以獲得正確估碼c2，得到與該碼字對應的發送信息。如果落在該a2區域之外，則表明信道噪聲對該信號產生了較大的干擾，超出了糾錯能力范圍，導致譯碼失敗。從圖1中可以看出，如果在接收信號中添加次級獨立的擾動噪聲，那么接收信號y在譯碼糾錯區域內的落點就會發生偏移，有可能會移動到可糾錯區域之內。如果譯碼過程中發生的錯誤相對較少[17]，那么信道接收信號有可能非常靠近其特定的糾錯區域。添加擾動噪聲產生的這種有益效果可以用隨機共振的現象來進行解釋，其定義是向信號中添加隨機獨立噪聲使其增強[18]。

圖1 譯碼空間示意圖

然而，若只是添加獨立的隨機噪聲，將使得接收信號的落點在譯碼空間中較為隨機，要使其回到正確可糾錯區域內可能需要嘗試多次。因此，本文利用卷積神經網絡強大的學習能力，從接收信號中提取特征，并根據接收信號與發碼間的偏離程度，動態地調節擾動噪聲的均值與方差，有效地將接收值y調回到其可譯碼糾錯區間內，通過對添加了擾動噪聲的接收信號重新計算似然比并譯碼，獲得有效的譯碼。

3.2 基于CNN擾動的極化碼譯碼算法

圖2是基于CNN擾動噪聲的極化碼譯碼流程圖，具體算法見表1。首先用SC譯碼器對信道接收值進行譯碼，估計值通過式(4)判決得到

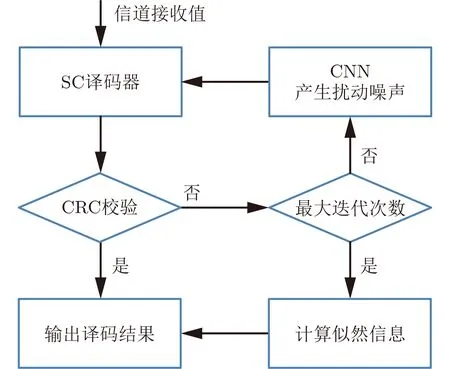
圖2 基于CNN擾動噪聲的極化碼譯碼流程圖

表1 基于CNN擾動噪聲譯碼算法

如果譯碼結果通過CRC校驗則表明譯碼成功，輸出譯碼結果，如果譯碼失敗則通過CNN對信道接收值提取特征，產生擾動噪聲np，將其加到y上，y'＝y+np，且使用y'代替y重新進行SC譯碼，這里對添加擾動噪聲后的接收信號LR進行修正，

其中，x(u?i)為譯碼結果序列通過極化碼編碼與BPSK調制后的向量。然后把最大值L(u?i)對應的譯碼結果作為輸出。

3.3 神經網絡設計與訓練

神經網絡利用類似于人腦的分層模型結構，從底層到高層對輸入數據逐級提取特征，在底層信號到高層語義之間建立起映射關系。本文設計的CNN網絡的參數如表2所示。

表2 CNN訓練相關參數

本文分兩個階段來訓練神經網絡，由于整個訓練過程是離線完成的，所以不會增加譯碼的復雜度。在這里，根據參考文獻[16]中的定義，使用了損失函數的正態性檢驗，以便測量接收值在譯碼糾錯空間的可能性，便于之后的似然信息的計算。損失函數定義為

其中，n表示真實噪聲向量，n'是CNN輸出噪聲向量，偏度D和峰度K定義為

(1) 進行了大量的模擬，使用極化碼編碼隨機信息比特，然后用SC譯碼帶有噪聲的BPSK符號，如果譯碼結果不通過CRC校驗，則表明譯碼失敗，需要加入擾動噪聲。在這種情況下，儲存一對y以及能夠使其回歸到譯碼可糾錯區域的擾動噪聲(對加入的隨機噪聲取負)np。

(2) 使用訓練數據訓練神經網絡以最小化損失函數。將數據庫分為兩組：訓練集和驗證集。訓練集用于訓練網絡，而驗證集用于避免過度擬合。雖然訓練質量受某些超參數的影響，但是在本文中，不關注這些超參數的優化，只選擇一組有效的超參數。

(3) 考慮到在加入擾動噪聲之后譯碼仍然失敗的情況，所以要循環迭代，重復加入擾動噪聲，這在第1階段是未被訓練的，所以要進一步訓練神經網絡，使其在上一次擾動噪聲的基礎上輸出正確的擾動噪聲。為了解決這個問題，在第2階段繼續訓練CNN，如圖3所示。在每次迭代中，基于CNN生成新的數據。然后，使用更新后數據庫強化學習來訓練神經網絡。

圖3 強化學習迭代訓練CNN

4 仿真結果分析

本文通過數值仿真來分析基于CNN擾動的極化碼譯碼算法的性能，以驗證該算法的有效性。極化碼碼長N為1024，碼率為0.5，信道條件為高斯白噪聲信道。圖4為不同譯碼算法的性能比較，從圖中可以看出，本文所提出的譯碼算法與SC譯碼算法相比可獲得約0.6 dB的增益，與添加隨機擾動噪聲(PA)相比(重譯次數門限T為10)，約有0.4 dB的增益。本文的譯碼算法在低信噪比時與SCL(L＝16)譯碼算法相比有接近0.1 dB的增益。但是，在信噪比＞2.75時，所提譯碼算法性能不如SCL(L＝16)譯碼算法。這是因為當信噪比較高時，噪聲較小，可提取的特征也減少，由CNN輸出的擾動噪聲將接收信號帶回可譯碼區域的能力下降，BER性能下降趨勢緩慢。本文認為這可能是由于神經網絡的識別能力隨著信噪比的提升下降而導致的。因此，針對這種現象，可以采用以下措施：(1)增加CNN網絡的訓練量，特別是在高噪聲比下的訓練數據，以提高CNN在高信噪比時對噪聲特征的識別能力，進一步提升所提譯碼算法的BER性能；(2)提高重譯的門限次數T，以提升高信噪比下所提算法的BER性能，可獲得與SCL(L＝16)結果相當的性能。

圖4 不同譯碼算法性能比較

為了進一步說明基于CNN擾動的Polar譯碼算法性能，圖5顯示了基于CNN的擾動譯碼算法與基于深度神經網絡(DNN)的擾動譯碼算法的性能對比，其中DNN最大迭代次數為10。從圖中可以看出，基于CNN的擾動譯碼算法性能更好，與基于DNN的擾動譯碼算法相比，性能約有0.4 dB的提升。

圖5 基于不同神經網絡的譯碼算法的性能比較

通過增加迭代的次數來進一步降低BER，圖6為不同最大迭代次數下的BER性能，從圖中可以看出，只設置1次迭代已經有相當不錯的性能，說明CNN已經可以產生較為滿意的擾動噪聲，隨著最大迭代次數的增加，性能逐漸增加，但是增益緩慢。考慮到譯碼復雜度，當T＝10時，譯碼效果最佳，有著較好的BER性能和較低的計算復雜度。

圖6 不同最大迭代次數下譯碼性能對比

與傳統SC算法相比，本文所提譯碼算法具有更多計算，因而復雜度較高。但是由于僅在SC譯碼失敗時才需要后續的計算，所以平均來說譯碼復雜度不高。圖7為不同譯碼算法的平均SC譯碼次數，從圖中可以看出，SC與SCL的譯碼次數是不隨著信噪比的增加而變化的，本文提出的譯碼算法只針對譯碼失敗的序列進行迭代，所以當信噪比提高時，發生譯碼失敗的概率減小，所以譯碼復雜度和SC譯碼算法相比幾乎相同。

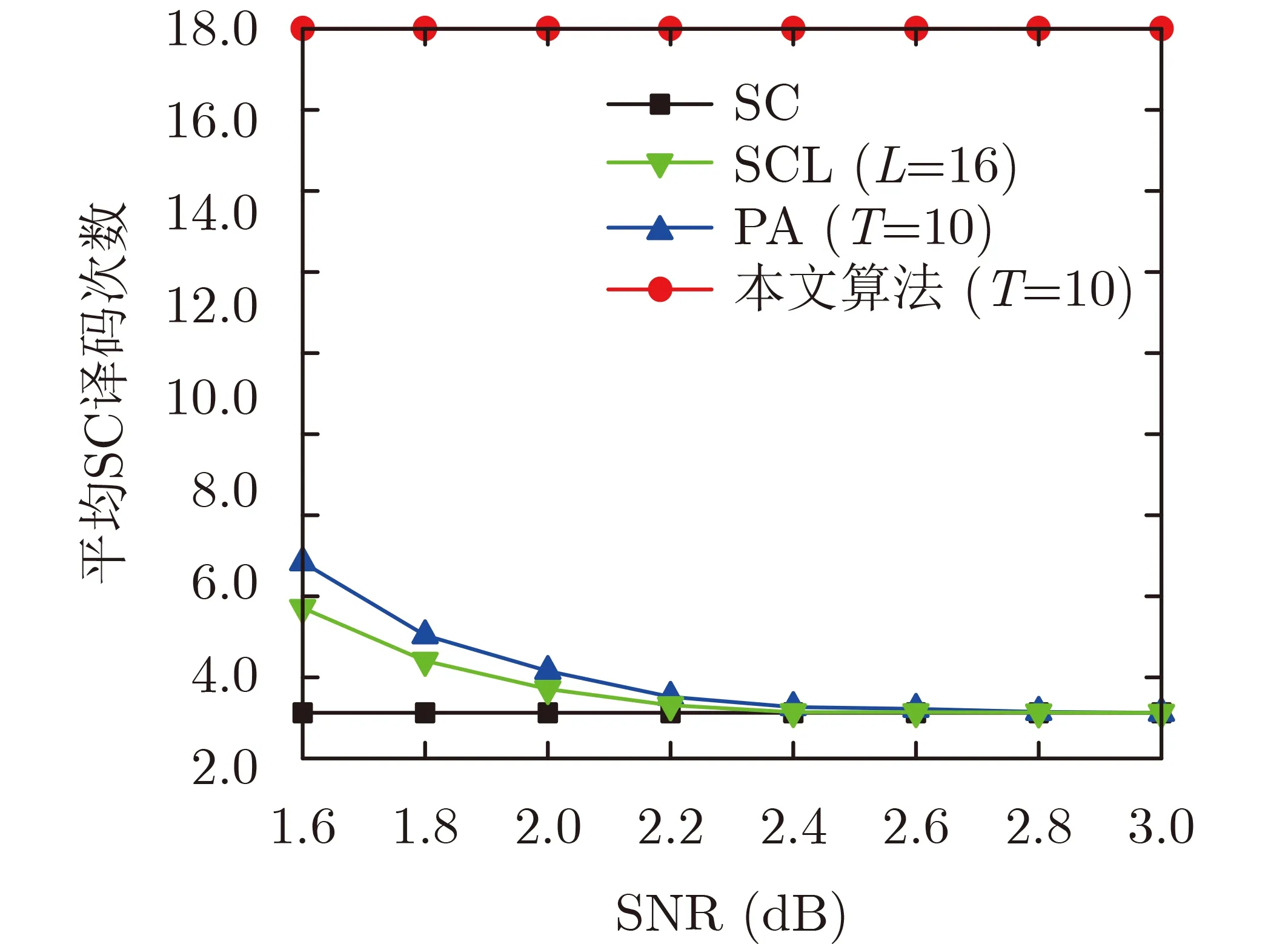
圖7 不同譯碼算法的平均SC譯碼次數

5 結束語

為了提升SC譯碼的性能，本文采用譯碼后處理技術，針對碼空間譯碼可糾錯區域的特點，通過CNN產生特定的擾動噪聲，使譯碼失敗的接收信號重新落在可糾錯區域之內，有效地提升了極化碼的SC譯碼算法的性能。仿真結果表明，在同等條件下，本文提出的算法與SC算法相比在復雜度較低的前提下具有更加優異的性能，與SCL(L＝16)譯碼算法相比，在譯碼性能相當的前提下有效地降低了譯碼時延。此外，本文以SC為例給出了基于CNN擾動噪聲譯碼方法，該思想也可以推廣到極化碼的其他譯碼算法或其他信道編碼的譯碼算法之中[19,20]。