一種選址定容的改進自適應粒子群算法

王欽亮，高桂革

(上海電機學院 電氣學院，上海 201306)

0 引言

分布式發電裝置接入配電網會在系統中形成雙向潮流，影響配電網的安全穩定運行[1]，分布式電源接入配電網系統的位置與容量更是決定對系統影響的程度，因此針對分布式發電接入配電網進行合理的選址定容顯得尤為重要。

針對分布式電源接入系統的選址定容，二次規劃法[2]等數學方法與遺傳算法[3]等智能算法廣泛應用于選址定容問題的求解。文獻[4]以有功損耗、電壓質量及分布式電源總容量為優化目標進行選址定容。文獻[5]以綜合成本、網損和電壓穩定裕度為目標函數的模型，并從形成的Pareto最優解集中選擇合適的最優解。文獻[6]以系統的電壓指標、網損指標、諧波指標綜合效果最好為目標，采用改進遺傳算法的多目標優化算法對所建立的模型進行求解。文獻[7]考慮網損、靜態電壓穩定和線路熱穩定3個指標，利用改進天牛須搜索算法求解。文獻[8]對配電網線路損耗、節點電壓和快速電壓穩定裕度指數建立目標函數，利用遺傳獅群算法優化算法求解目標。文獻[9]以各節點電壓、可接入最大功率及線路電流作為約束，以網損最小作為目標，應用改進螢火蟲算法對模型求解。

本文提出了一種綜合考慮分布式電源接入系統引起的網損變化率、分布式電源接入節點負荷占總負荷比重的綜合比率。構建了以經濟性為目標函數的模型，提出了一種改進自適應粒子群算法，設置不同方案進行仿真并與粒子群算法對比，仿真的結果說明分布式電源接入系統位置和容量對配電網的重要影響，從而驗證此綜合比率方法的的可行性及算法的有效性。

1 分布式電源接入配電網選址定容

1.1 分布式電源接入位置對配電網影響

牛頓-拉夫遜潮流算法在數學上用來求解非線性方程式非常有效，在配電網的潮流計算的應用中有收斂速度快和迭代次數少的優點[10]。因此本文采用牛頓-拉夫遜潮流算法對DG接入配電網后系統網損及電壓進行定量計算研究。

采用 IEEE33節點配電網作為算例[11]，將一個有功功率為500 kW 功率因數為0.9且視為PQ節點的DG接入IEEE33配電網中的3和15節點，通過牛頓-拉夫遜潮流的方法求解相關網絡參數，得到支路網損和節點電壓曲線分別如圖1、如圖2所示，得到的結果如表1所示。

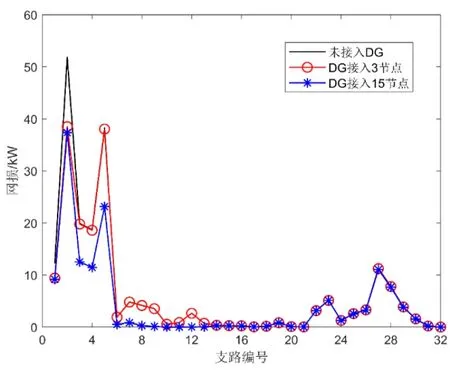
圖1 DG 接入系統網損圖Fig.1 DG access system network loss diagram

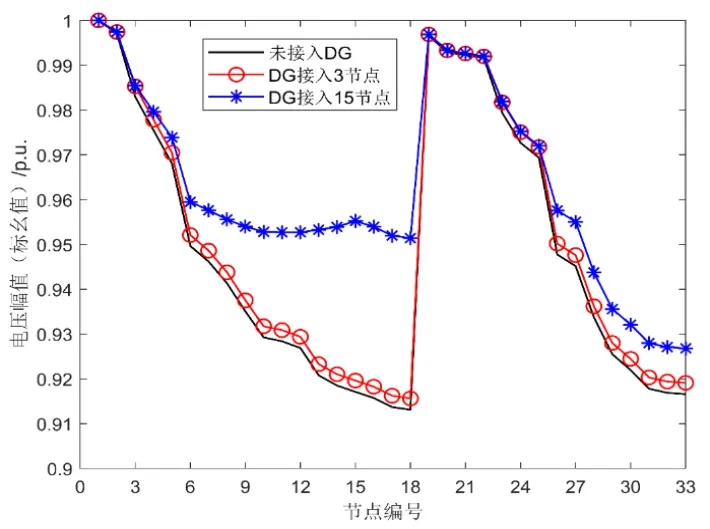
圖2 DG 接入系統電壓分布圖Fig.2 DG access system voltage distribution diagram

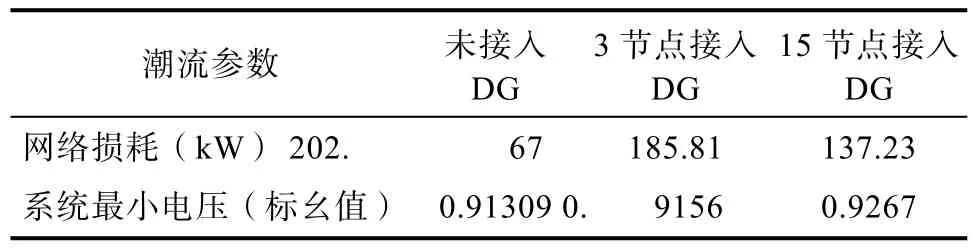
表1 單節點接入DG潮流參數比較Tab.1 Comparison of power flow parameters of single node connected to DG

當系統接入 DG后配電網的網損會比系統未接入DG時小，并且將DG接入到3節點和15節點的系統網損有不同，這表明將相同容量的 DG接入到系統的不同節點位置，配電網的網絡損耗也不同；配電網中接入DG會對系統的電壓有抬升作用，DG接入配電網節點位置不同，對系統電壓的抬升效果也不同。

DG輸出的有功功率和無功功率與配電網支路上的阻抗相關，并且輸出的功率會影響配電網網損大小及節點電壓。考慮DG接入后網損和線路阻抗對配電網潮流的影響，提出一種綜合考慮DG接入配電網引起的網損變化率與所接入節點的負荷占總負荷比重的綜合比率方法，以此確定DG接入配電網的最佳位置，如式（1）所示：

式（1）中，Z代表綜合比率；W代表DG接入后引起系統網損的變化率；F為DG所接入的節點負荷占總負荷的比重；k1、k2代表權重為常數。

DG接入后系統網損變化率W與 DG所接入的節點負荷占總負荷的比率F的公式如式（2）（3）所示：

式（2）中，wy為未接DG時系統網損；wx為 DG接入后系統網損；式（3）中，fj為 DG所接入的節點負荷量，fz為系統負荷總量，負荷的單位KVA。

1.2 分布式電源接入容量對配電網影響

DG接入容量也會對系統潮流帶來影響，選取IEEE33配電網15節點與29節點，其節點位置相對于母線有所不同。依次接入容量為100 kW 功率因數為0.9的DG，保證功率因數均為0.9，接入容量依次增大 200 kW，利用牛頓-拉夫遜潮流計算法進行求解，所得圖像分別如圖3、4所示。

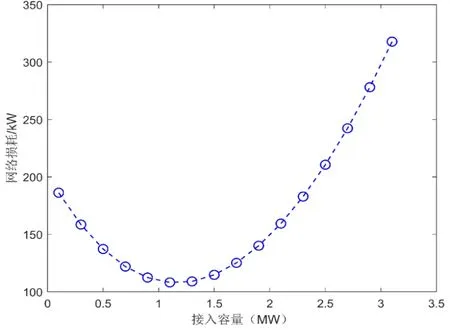
圖3 不同容量接入15節點網損圖Fig.3 Network loss diagram of 15 nodes with different capacities

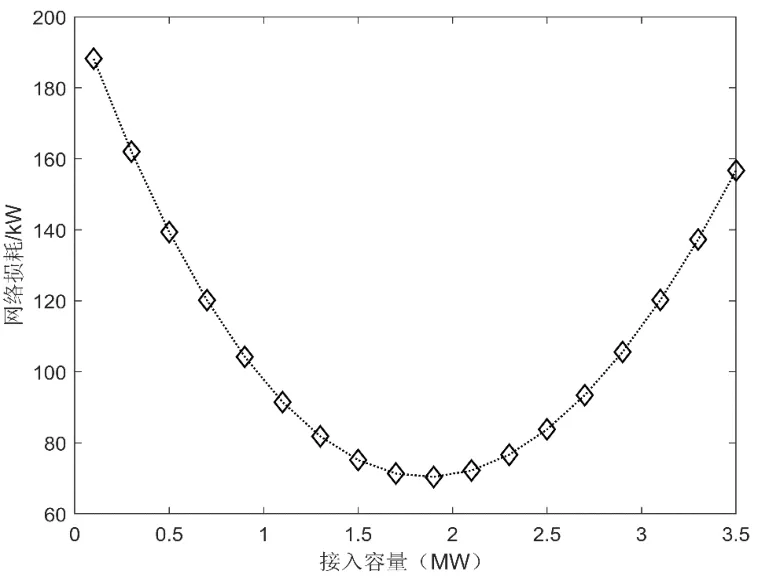
圖4 不同容量接入29節點網損圖Fig.4 Network loss diagram of 29 nodes connected to different capacities

在相同位置接入不同容量的DG，配電網網損值會隨著DG接入容量的變化而改變，并且各節點的最小容量值不相同。節點的選擇會影響 DG接入最佳容量的確定，即分布式電源的接入節點最佳容量取決于DG接入節點的位置。

2 目標函數構建與約束條件

為研究分析分布式電源接入位置以及引起的接入最佳容量大小對配電網的經濟性與穩定性的具體影響，文中構建經濟性最優和無功電容投切量最小的多目標函數。

2.1 目標函數

（1）網絡損耗

配電網網絡損耗的計算公式為：

式（4）中Ploss為總有功網絡損耗；L為配電網網絡支路數；Ri為第i條支路的電阻值；Ii為流過第i條支路的電流。

（2）綜合成本

DG的綜合成本是由分布式電源的投資運行成本、有功損耗費用以及投切電容器組費用組成。系統并聯電容器可以較好的滿足配電網無功功率的補償需要，且為就地補償，即無功補償電容器的接入位置與DG接入位置相同。由于并聯電容器也與經濟性相關，在滿足系統穩定運行的情況下，應合理接入，因此綜合成本公式為：

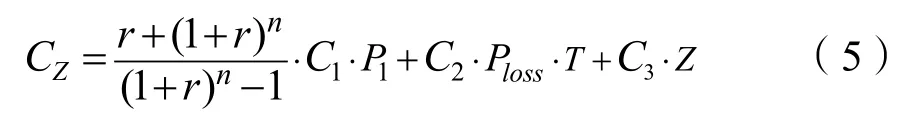
式中r為貼現率；n為 DG使用年限；C1為DG投資費用，單位為萬元/MW，P1為DG接入的有功功率，單位MW；C2為網絡損耗費用；T為負荷最大利用小時數；C3為每組并聯電容器的價格；Z為并聯電容器組數。

2.2 約束條件

（1）節點功率平衡約束：

式（6）中Pir與Qir為節點i的有功、無功注入；Ui與Uj為節點i和j的幅值；Gij與Bij分別為電導和電納；θij為節點i和節點j電壓相角差。

（2）節點電壓約束：

式（7）中Ui為第i個安裝節點的電壓值；Ui,max與Ui,min為節點電壓的上下限。

（3）支路功率約束：

式（8）中Sl為支路L的傳輸功率，Sl,max為上限。

（4）無功補償投入裝置組數約束：

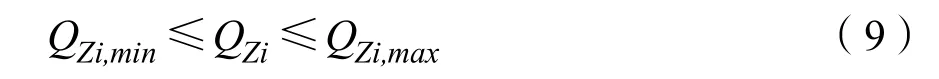
式（9）中QZi為第i個安裝節點無功補償設備的投切組數，QZi,max與QZi,min為上下限。

3 分布式電源選址定容模型求解

3.1 改進粒子群算法

美國電氣工程師Russell. Ebherhart和社會心理學家 James. K enndy根據鳥群覓食行為提出粒子群優化算法（Particle Swarm Optimization，PSO）簡稱粒子群算法[12]。PSO設置的參數少，求解速度快，搜索效率高，易于收斂到全局最優解，適合對多目標問題尋優。

在粒子群算法中，每個個體被當作微小的粒子。假設共有M個粒子，這些粒子在N維的搜索空間中形成一個群體，每個粒子都有自己的位置xi和速度vi，其中i=1,2,…,M。每個粒子的位置就是一個潛在的解，而速度則決定了粒子“飛行”的方向和單次的距離。此外，每個粒子都有自己的適應值，其適應值的大小由待優化的目標函數決定。粒子群算法就是通過適應值大小來判斷解的優劣，并追隨著當前的最優解，經過反復的迭代尋找到全局最優解。粒子群速度更新公式如式（10）所示，位置更新公式為：

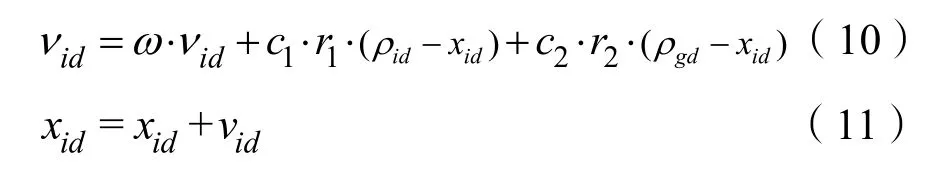
式（10）中c1和c2為學習因子；r1和r2是范圍在 0～1的隨機數；ρid和ρgd分別為粒子的自適應度和全局適應度。

粒子群算法的優勢是不用調節過多參數，但是粒子群算法中的參數直接影響算法收斂性能，其中慣性權重ω是最重要的參數，設計合理的慣性權重ω，是避免算法求解陷入局部最優解的關鍵，通過對慣性權重ω的改進達到更好的收斂效果。

為了提升算法的收斂性能，對PSO中的慣性權重進行自適應改進，如式（12）所示：

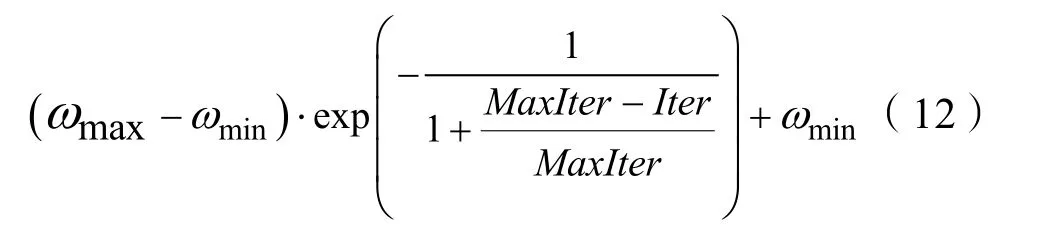
式（12）中ωmax與ωmin為慣性權重的最大值和最小值，MaxIter為最大迭代次數。Iter為當前迭代次數。

PSO學習因子也對收斂性以及算法尋優有一定的影響，因此根據式（13）所示，對學習因子c1、c2進行自適應改進。

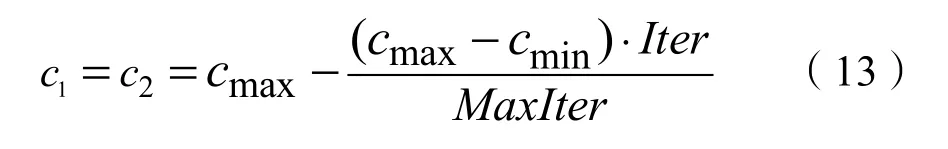
式（13）中，cmax與cmin為學習因子的最大值和最小值。

3.2 目標模型的求解

利用改進的粒子群算法對建立的模型進行求解，流程如下

（1）通過編碼的方式，對分布式電源與無功補償電容接入位置與接入容量進行限定與約束，設置粒子群的粒子速度范圍作為接入無功補償組數的限制。初始粒子種群，包括粒子速度，位置等。設置種群規模，最大迭代次數與收斂精度。

（2）計算每個粒子的適應度值Fit[i]

（3）將每個粒子的適應度值Fit[i]和個體極值ρbest(i)比較，如果Fit[i]＞ρbest(i)，則用Fit[i]替換掉ρbest(i)。

（4）對每個粒子的適應度值Fit[i]在和全局極值gbest(i)比較，如果Fit[i]＞gbest(i)，則用Fit[i]替換掉gbest(i)。

（5）根據式（10）和式（11）更新粒子的位置xi和速度vi，根據式（12）和式（13）更新自適應慣性權重與學習因子，

（6）如果滿足結束條件即滿足給定收斂精度或者到達最大循環次數退出，否則返回（2）。

具體流程圖如圖5所示。

圖5 改進粒子群算法求解模型流程圖Fig.5 Improved particle swarm algorithm solution model flowchart

4 選址定容算例分析

采用IEEE33節點作為算例，系統電壓等級為12.66 kV，總有功負荷為3.715 MW，總無功負荷為2.30 Mvar，IEEE33節點圖如圖6所示。

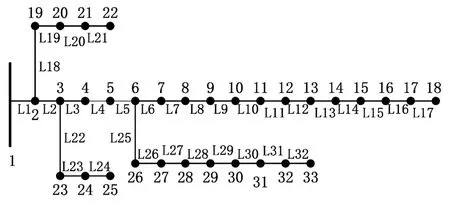
圖6 33 節點配電網圖Fig.6 33-node distribution network diagram

將有功功率為600 kW、無功功率為290.59 kvar且為PQ節點類型的 DG接入到IEEE33系統的各個節點，根據本文所提出的綜合比率公式求解，其中k1與k2都取常值為 0.5。所得結果如表2所示，求解出的綜合比率圖如圖7所示。

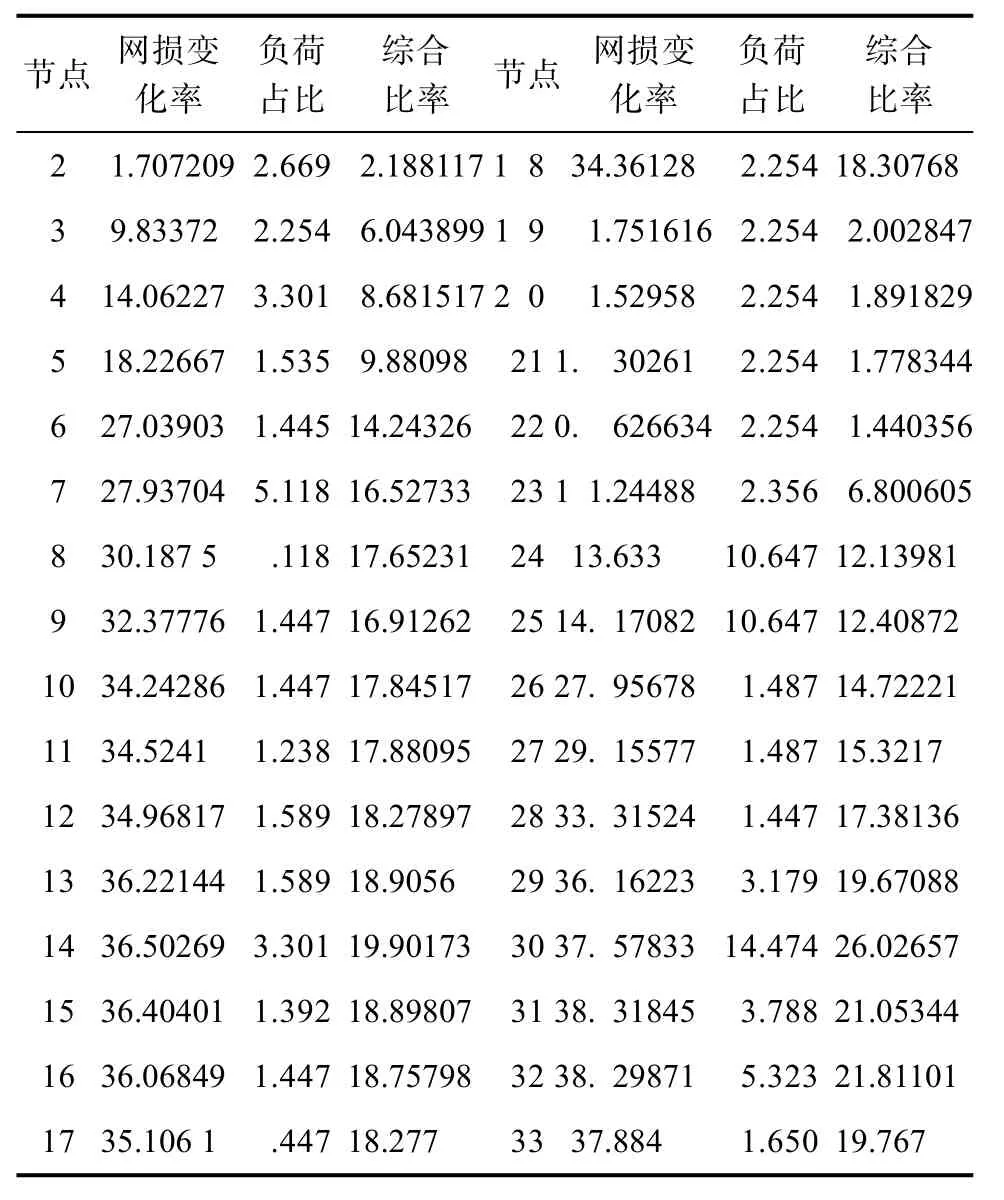
表2 各節點網損變化率、符合占比、綜合比率數據（%）Tab.2 Data on the change rate of the network loss of each node, the proportion of compliance, and the comprehensive ratio data

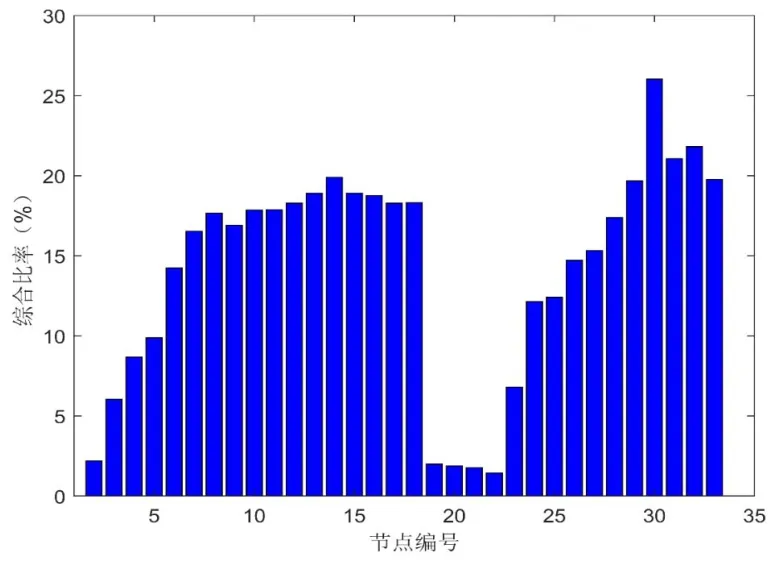
圖7 各節點綜合比率柱狀圖Fig.7 Histogram of comprehensive ratio of each node

綜合比率的值越大，所在節點對系統的影響就越大，應作為優先考慮的接入點。由數據分析可知，節點30、32、31、14、33、29、13、15節點的綜合比率值較大，這些節點應作為優先考慮節點接入系統配電網中。

設置每個節點無功電容器組投切的最大數為5組,每組無功電容器容量為10 kvar。改進粒子群的相關參數作如下設定。粒子個數為 100，粒子群的學習因子cmax=2,cmin=1，慣性權重分別為ωmax=0.9,ωmin=0.5,最大迭代次數MaxIter=200,收斂精度為10-10。

為研究分布式電源接入位置與容量對電網經濟性及穩定性影響，設置如下方案進行對比分析：將3個有功功率為600 kW 且可參與無功調節的DG分別接入隨機選取的節點，選取 9節點、24節點、28節點接入DG，此為方案一；將相同DG接入綜合比率大的節點，選取14、30、32節點接入 DG，此為方案二。利用粒子群算法與自適應改進粒子群算法進行模型的求解，所得數據分別如表3與表4所示。

表3 方案一求解數據Tab.3 Solution one solves the data

表4 方案二求解數據Tab.4 Solution two Solve the data

對表3與表4的數據進行分析，說明相關的問題。通過表3數據可以看出，利用改進后的粒子群算法求解系統的網絡損耗要比未改進粒子群算法求解出的損耗要小，并且綜合成本也較比未改進算法求解出的結果要少，表4得到數據也具有相同的結論，由此說明提出的自適應改進粒子群算法的有效性。

將表3數據與表4數據進行對比，方案二系統的網絡損耗與綜合成本相比于方案一都少，這說明分布式電源接入系統的節點位置對經濟性與配電網系統穩定性都產生影響，在綜合比率較大的節點接入分布式電源有利于提高系統的穩定性，且具有更好的經濟性。

5 結論

分布式電源接入配電網的節點位置與容量，都會對系統的穩定性運行造成影響，并且分布式電源最佳容量取決于其接入系統的位置，因此合理的進行DG接入系統位置的確定尤為重要。

（1）利用牛頓-拉夫遜潮流計算，結合提出的考慮網損變化率和負荷占比的綜合比率公式，確定綜合比率較大的節點即最佳DG接入節點。

（2）構建以經濟性為目標的函數，提出一種自適應改進的粒子群算法對目標函數進行求解，并與未改進的粒子群算法相比較，說明該算法的可行性。

（3）對DG接入綜合比率較大點的經濟性與網損和 DG隨機接入系統節點所得的結果相對比，說明提出綜合比率公式的可行性。

該方案對 DG接入配電網最佳位置及容量確定的合理性規劃，提高配電網系統經濟性與穩定性運行，有一定的參考價值。