某彈內膛減振刀桿設計及振動特性分析
宋成俊,李艷飛,任建榮
(1.海裝沈陽局駐沈陽地區第三軍事代表室,遼寧 沈陽 110045;2.遼沈工業集團有限公司,遼寧 沈陽 110045)
0 引言
某彈在生產過程中其內膛的加工是十分重要的一道工序,主要是依靠車削的方法實現對內膛的加工。但是由于內膛車削與普通零件的外表面車削不同,刀桿需要從彈體口部伸到炮膛內部進行作業[1,2],所需的刀桿長度要遠遠大于普通車刀的刀桿(其長度達到近300 mm),因此在車削加工時刀桿在承受切削力的情況下很容易產生振動和變形。針對刀桿在某彈內膛加工時存在的問題,急需設計一種能夠滿足內膛加工要求的減振刀桿。本文針對某彈加工的這一需求,設計了一款減振刀桿,并通過ANSYS Workbench軟件分析其加工的可靠性。
1 刀桿結構設計
為了達到減振效果設計了一種長度為280 mm、直徑為32 mm的減振刀桿結構。加工時刀桿前端為刀尖角為35°的菱形刀片,以保證所受的切削力較小,起到較好的減振效果。所設計的減振刀桿結構如圖1所示。
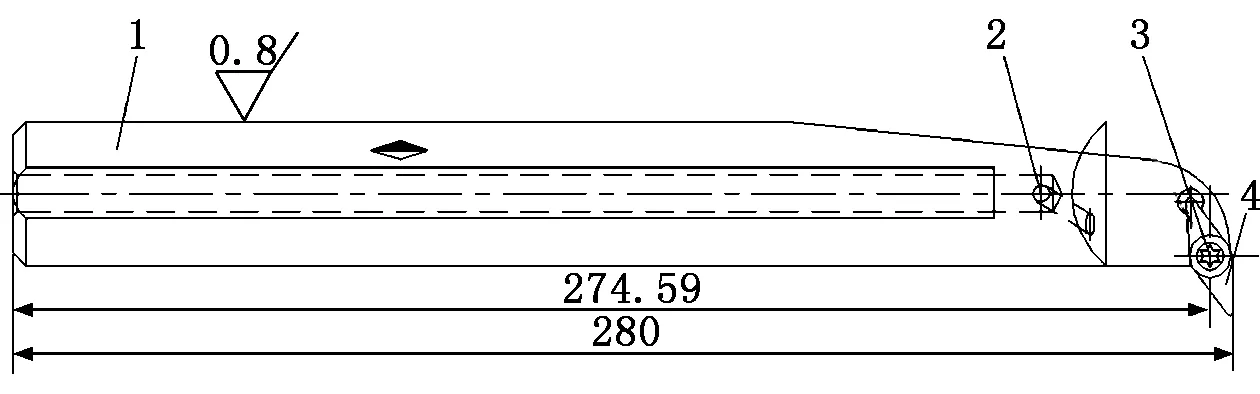
1-減振刀桿;2-工藝堵;3-螺釘;4刀片
根據刀片的結構尺寸,可計算刀桿在進行內膛切削加工時的切削力。切削力可以分解為主切削力Fc、背向力Fp以及進給力Ff,三個力[3]的表達式分別為:
(1)
(2)
(3)
其中:CFc、CFp、CFf分別為決定于被加工材料和切削條件的系數;xFc、xFp、xFf分別為三個分力公式中背吃刀量ap的指數;yFc、yFp、yFf分別為三個分力公式進給量f的指數;nFc、nFp、nFf分別為三個分力公式中切削速度Vc的指數;KFc、KFp、KFf分別為當實際加工條件與所求得的經驗公式的條件不符時各種因素對切削力的修正系數的積。
已知刀片的材料為硬質合金,查文獻[4]可得:
CFc=270,xFc=1.0,yFc=0.75,nFc=-0.15;CFp=199,xFp=0.9,yFp=0.6,nFp=-0.3;CFf=294,xFf=1.0,yFf=0.5,nFf=-0.4。
以58SiMn高強度鋼的加工為例,由該材料的強度極限為σb=1 080 MPa可得主切削力Fc、背向力Fp以及進給力Ff的切削力修正系數分別為:
由刀尖圓弧半徑R=0.8 mm(查表時取1.0 mm),刀片前角ro=15°(查表時取20°),主偏角kr=93°(查表時取90°),刃傾角λs=0°,查文獻[4]可得主偏角修正系數KkrF、前角修正系數KroF、刃傾角修正系數KλsF以及刀尖圓弧半徑修正系數KrF在主切削力Fc、背向力Fp以及進給力Ff三個分力方向上的修正系數為:
KkrFc=0.89,KroFc=0.9,KλsFc=1.0,KrFc=0.93;
KkrFp=0.50,KroFp=0.7,KλsFp=1.0,KrFp=0.82;
KkrFf=1.17,KroFf=0.7,KλsFf=1.0,KrFf=1.0。
所以可計算得:
KFc=FmFc×KkrFc×KroFc×KλsFc×KrFc=1.090 18
KFp=FmFp×KkrFp×KroFp×KλsFp×KrFp=0.569 60
KFf=FmFf×KkrFf×KroFf×KλsFf×KrFf=1.360 80
再由刀具切削時的切削參數:背吃刀量ap=0.6 mm,進給量f=0.2 mm/r,切削速度Vc=64 m/min,并考慮到工作效率為9.81,將已知數據代入式(1)~式(3)可計算得:
Fc=9.81×270×0.61.0×0.20.75×64-0.15×1.090 18≈277.669 22 N.
Fp=9.81×199×0.60.9×0.20.6×64-0.3×0.569 60≈76.770 12 N.
Ff=9.81×294×0.61.0×0.20.5×64-0.4×1.360 80≈199.528 48 N.
由計算結果可以看出,所設計的車刀刀片在對58SiMn這種彈體材料進行加工時,刀片所受的切削力并不大,但是還需進一步分析切削力對刀桿的影響。
2 刀桿和刀片的強度分析
安裝有刀片的刀桿在對彈體進行車削過程中,必然會受到來自刀片的傳遞力,而刀桿的形狀為不規則桿件,采用傳統的材料力學計算方法無法校核其結構強度,因此在強度校核時采用有限元方法進行計算,選用ANSYS Workbench 作為計算工具。
刀桿的強度分析應用ANSYS Workbench的靜力學分析模塊,該模塊可以完成對模型所受的應力、應變以及變形的分析,其本質是基于靜力學平衡方程進行計算的,在求解過程中求解器所遵循的靜力平衡方程為:
[K]{u}={F}.
(4)
其中:[K]為剛度矩陣;{u}為結構位移;{F}為靜力載荷。
分析時使用UG三維仿真軟件進行模型建立并將刀桿和刀片進行裝配,然后將UG中裝配好的三維模型導成STP格式的文件,以便導入到ANSYS Workbench中進行分析。
2.1 模型導入及網格劃分
打開ANSYS Workbench軟件并進入靜力學分析模塊Static Structural,將UG建好的模型進行導入。模型導入成功后進行材料模型的設置,刀桿的材料為42CrMo,刀片的材料為硬質合金,通過查找相關資料,這兩種材料的材料參數[5-8]分別如表1和表2所示。

表1 42CrMo材料模型參數

表2 硬質合金材料模型參數
添加材料后進行接觸的定義,對于刀片和刀桿采用Contact Redion接觸;接觸定義完成后即可進行網格劃分,網格尺寸設置為2.5 mm,最后得到184 562個節點、129 198個單元,劃分網格后的模型如圖2所示。

圖2 劃分網格后的刀桿和刀片
2.2 添加約束及載荷
劃分完網格后要添加約束和載荷,經分析刀桿在加工內膛時一端為固定端,因此在刀桿的后端面添加固定約束,而在加工過程中刀桿所受的載荷主要來自于刀片,根據前面的分析可知刀片所受的力主要是切削過程中的切削力,前面已經通過理論計算得到切削力的值,這里只需在刀片的刀尖處添加Force,然后將理論計算得到的受力值添加到x、y、z三個方向,添加約束和載荷后的模型如圖3所示。

圖3 添加約束和載荷后的模型
2.3 靜力學分析
在載荷和約束添加后就可以進行靜力學解算,對于刀桿和刀片主要要查看的結果為變形和應力,因此添加Total Deformation以及Equivalent Stress來查看變形和等效應力,計算后的云圖分別如圖4和圖5所示。

圖4 刀桿和刀片的變形云圖

圖5 刀桿和刀片的等效應力云圖
由圖4可以看出:在進行內膛切削過程中,刀桿和刀片的最大變形為0.172 27 mm,出現在刀桿切削的一端和刀片整體,這是因為在切削過程中整個模型近似為一個懸臂梁,受力一端變形必然最大。從圖5中可以看出:模型的最大等效應力為26.889 MPa,遠遠小于刀片和刀桿的屈服強度,出現位置分別為刀片與刀桿鏈接的螺紋孔處、刀片和刀桿的接觸位置以及刀桿固定端的邊緣,這是因為在刀片的中心孔處易產生應力集中,而刀片與刀桿的接觸屬于線接觸,所以接觸位置受力較大,對于刀桿部分來講,其固定一端的邊緣由于所受到的力矩較大,因此受力端面產生了較大的應力。但是從計算結果來看,正常工作時刀片和刀桿的受力和變形都不是很大,可以滿足彈體內膛的加工要求。
3 刀桿和刀片的振動分析
為了防止刀桿和刀片在加工過程中由于受力而發生共振,需要對刀桿和刀片進行結構振動情況分析。ANSYS Workbench為振動分析提供了兩個模塊,即無應力的模態分析模塊和有預應力的模態分析模塊,由于在車削過程中刀片和刀桿受切削力的作用,因此分析時選用有預應力的模態分析。
經過計算,刀片和刀桿的前6階固有頻率如表3所示,各階固有頻率所對應的變形情況如圖6所示。

表3 刀片和刀桿前6階固有頻率

圖6 刀片和刀桿的前6階模態陣型圖
由圖6可以看出:刀桿和刀片的最大等效變形量在51.385 mm~79.015 mm之間;1階振型以刀桿的固定端為端面繞z軸擺動,擺動幅值沿固定端向刀桿逐漸增加;2階振型與1階振型類似,但不同的是在擺動過程中刀桿是繞y軸擺動,幅值的變化情況與1階振型相同;3階振型同樣是以刀桿的固定端為端面,以近似刀桿中間端面繞z軸作扭動,擺動幅值變化不規則,但是刀桿另一端變形最大;4階振型與3階振型相似,不同的是該振型下以近似刀桿中間端面為中心繞y軸作扭動,擺動幅值與3階振型相同;在5階振型下刀桿同樣為固定端面,此時整個模型以刀桿中心軸為基準,繞該軸作扭轉運動,擺動幅值由中心向兩端逐漸增大;在6階振型下刀桿一端為固定端,近似以刀桿中間端面為中心在其兩側作方向相反的扭動,擺動幅值與3階和4階振型類似。
由以上分析可以看出,在正常工作情況下刀桿和刀片的強度和變形都能滿足使用要求,而在進行振動分析時,在切削過程中如果發生共振,其變形量較大,但是從分析結果可以看出,發生振動的頻率較大,在加工內膛時很難發生這樣頻率的振動,因此所設計的內膛刀桿能夠滿足使用要求。
4 結束語
某彈內膛的加工質量主要由內膛車刀的刀桿來保證,所使用刀桿在切削加工時的強度和振動是能否實現質量要求的前提。本文應用有限元分析的方法驗證了所設計的刀桿在內膛加工時的可靠性,為新刀桿在生產中的應用提供了必要的依據。

