變分推理的概率高斯/非高斯過程監測

任珈儀，任世錦，潘劍寒，楊茂云，李新玉

（1.南京郵電大學理學院，江蘇南京 210023；2.江蘇師范大學計算機學院，江蘇徐州 221116；3.中國礦業大學機電工程學院，江蘇徐州 221116）

隨著現代流程工業不斷朝著復雜化方向發展，穩定的工業產品質量和安全高效的生產成為科研技術人員和企業管理者主要關注的問題。近年來，基于數據驅動的過程監測理論和技術能夠通過生產和工藝數據分析快速幫助操作人員和工程師了解生產過程相關知識，及時處理異常現象，在實際應用中取得了較好的效果，受到人們的普遍關注[1-4]。典型的過程監測方法主要有主元分析、偏最小二乘、高斯混合模型等統計分析方法。另外，流形學習具有描述數據幾何結構的強大能力，在非線性維數約簡、描述數據局部特性的方面具有出色表現，也是提高故障診斷的準確性和可理解性的可行方法[5-6]。另外，流形學習與其他統計分析技術進行結合，可以提高統計分析方法描述數據幾何結構的能力，能夠更好地刻畫數據總體分布，這也成為流形學習研究的重要方向，極大擴寬了流形學習的應用范圍[7]。

高維過程數據的本質特性往往可以由隱藏低維空間的數據描述，另外，過程工況切換、外部環境干擾等因素會導致測量數據具有明顯的隨機不確定性。近年來，隱變量模型技術在高維數據信息提取方面的優勢以及概率圖理論對隨機數據建模的強大能力已經成為過程故障檢測和軟測量建模的重要方法，已在實際應用中取得滿意的效果[8]。一般來說，過程變量集往往由高斯分布變量與非高斯分布變量組成，不同過程變量的噪聲水平可能有所差異。即使在過程平穩運行狀態，仍然有部分過程變量服從非高斯分布。然而，一些過程監測算法仍然假設過程(隱)變量服從高斯分布，這種假設會影響過程監測精度[9-10。]獨立成分分析（Independent Component Analysis,ICA）與主元分析(Principal Component Analysis,PCA)分別用于描述非高斯數據和高斯數據，文獻[11]提出KICA-PCA 的兩階段非線性過程在線監測算法，利用學生t-分布能夠近似高斯/非高斯分布。文獻[3]提出了基于t-分布的PICA 算法，并在此基礎上提出了兩階段概率ICA（Probabilistic ICA,PICA）與概率PCA（Probabilistic PCA，PPCA）方法，分別提取數據中高斯和非高斯成分，有利于理解運行模式。上述抽取高斯/非高斯成分方法均通過兩階段方法抽取不同類型成分，并且假定各個變量噪聲水平相同，無法同時抽取高斯和非高斯成分。

基于上述討論，考慮到隱變量模型在數據降維和信息提取的優勢以及概率圖理論描述隨機數據的有效性[12-14]，設計一種基于學生t-分布高斯/非高斯成分提取框架，并用于過程故障診斷。該方法使用變分推理(Variational Inference,VI)自動確定模型參數和模型選擇，保證了模型性能的提高。該方法還能夠同時提取過程的高斯/非高斯成分,實現兩種成分的折中平衡，提高了混雜過程的信息提取能力。文中建立了高斯/非高斯以及殘差空間的故障監測統計量，有利于提高工業過程的安全性和認識水平。最后，使用TE 模型對提出算法進行仿真驗證，結果表明，所提出的模型能夠有效運用于高斯/非高斯分布過程監測，且具有良好的魯棒性。

1 高斯/非高斯成分概率模型

假設隱變量和觀測變量x之間具有如下線性關系：

其中，P∈?D×d為類似PCA 負荷矩陣的權重矩陣，且滿足PTP=Id∈?d×d；t∈?d×1為服從正態分布N(0,Id)的隱變量；Id為單位矩陣且d＜D；觀測噪聲ε服從高斯分布N(0,Λ-1)，Λ=diag(β,β2,β1) ；s∈?r為相互獨立的非高斯信號源，滿足。由式（1）可以看出，觀測數據的變化能夠由隱空間中非高斯和高斯成分表示，由此可以更好地理解過程機理。值得注意的是，非高斯信號和高斯信號是相互獨立的，定義如下隱變量先驗和觀測變量條件分布形式：

其中，Λ為對角矩陣。傳統方法假定多個高斯混合可以近似非高斯信號，但是混合信號的數量難以確定。由于t-分布可以看作無限多個不同高斯分布信號的混合形式，因此可以使用t-分布表示非高斯信號[9]。在實際中，通過調節自由度值使得t-分布近似非高斯分布。非高斯源信號的每個維度變量sk的分布形式為：

在介紹推理方法前，先給出文中模型概率結構圖，如圖1 所示。定義隱變量集合Δ={T,S,U}，其余模型參數記為Θ，由圖1 可以看出變量之間的依賴關系，對數完全似然函數形式為：

圖1 高斯/非高斯混合概率模型結構圖

無法直接求取似然函數最大優化問題的閉解，MCMC 和貝葉斯變分推理方法是關于學習參數后驗分布的常用方法。由于MCMC 存在計算效率以及收斂性問題，因此文中使用貝葉斯變分推理方法(VI)學習參數的后驗分布。

2 變分推理的模型參數學習

基于變分理論[15]，對數完全似然函數具有如下關系：

在實際中，將隱空間的方差約束為單位方差進行分析，每個隱空間的方差與自由度關系一般滿足。實際中定義自由度的最小取值為vk=2.5。ICA 維度采用交叉驗證方法確定，即首先使用范數進行維度范圍的初選，然后使用交叉驗證并結合模型的復雜度來進行進一步選取。使用PPCA 對矩陣P進行初始化，其他參數可以通過隨機初始化獲取，這樣可以大大提高算法的收斂速度。

3 故障檢測統計量的構建

其中，a為置信度，dt為高斯隱變量的維數，D為觀測數據維數。使用核密度估計方法計算非高斯成分監測統計量I2的控制限，控制置信度同樣設置為a。

4 仿 真

為了評價所提出方法的有效性，仿真實驗使用Tennessee Eastman（TE）測試仿真平臺。該平臺是一個典型的化工模型仿真平臺，系統由連續攪拌式反應釜、分凝器、氣液分離塔、汽提塔、再沸器和離心式壓縮機等操作單元組成，常用故障監測仿真見文獻[3]。TE 過程的流程示意圖如圖2 所示。

圖2 TE過程流程示意圖

TE 過程共有41 個測量變量和12 個操控變量，選取與文獻[11]相同的22 個變量作為故障監測變量。訓練樣本和檢測樣本的采樣間隔均設定為3 s，采集960 個過程平穩狀態樣本作為正常訓練樣本。過程平穩運行8 h 之后加入故障，整個采集過程中系統共運行48 h，共采集960 個樣本點。在建模階段，對所有樣本均歸一化預處理。根據模型訓練結果，采用交叉驗證方法確定了27 個維度的隱空間。考慮到幾個隱變量自由度相差較小的情況，文中選取自由度大于40 的隱變量作為高斯分布變量，非高斯成分數量為8，高斯成分數量為19，置信度取99%。對于難以準確檢測的故障3 和故障9，利用文中方法進行檢測。從圖3 可以看到，文中方法的3 個統計量均能夠檢測到過程的變化，并能夠準確指示過程故障。同樣，由圖4 可知，文中模型能夠檢測到故障9。上述故障檢測結果表明，3 種監測統計量可以相互補充，從而有效提高系統的故障檢測性能。

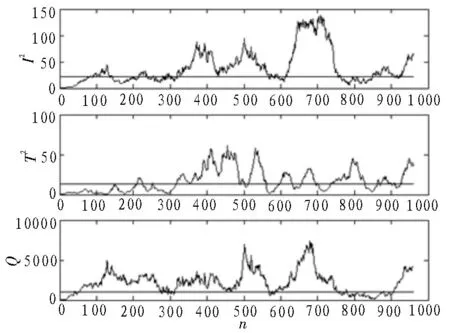
圖3 文中方法故障3仿真結果

圖4 文中方法故障9仿真結果

為了進一步說明文中方法的有效性，表1 中列出了使用文中方法與ICA-PCA、PICA-PPCA 方法檢測故障3 和故障9 時各個統計量檢測結果。從表1可以看出，文中方法的Q統計量獲得了最好的檢測效果，對于檢測過程中的微小、潛在故障的效果是明顯的，漏檢率低于其他監測方法，也在一定程度上提高了過程運行的安全性。

表1 故障3和9的檢測結果

5 結論

針對高斯/非高斯混雜過程魯棒建模問題，提出了高斯/非高斯成分抽取統一框架，克服了現有兩階段高斯/非高斯信息抽取算法存在的計算量大及忽略了兩類信息的關聯性等缺點。文中詳細給出了變分推理算法學習模型參數方法，自適應確定獨立成分數量和高斯成分數量，克服了現有方法忽略兩類信息的關聯性問題。最后在TE 平臺對難以檢測的故障3 和故障9 進行了仿真實驗，并與其他方法進行對比。仿真表明，所提算法能夠準確抽取高斯/非高斯信息，故障檢測統計量之間具有一定的互補性，表現出很好的建模和監測效果，具有很好的魯棒性能。

需要注意的是，文中方法為線性特征抽取方法，對于動態非線性系統還需要對該方法進行進一步改進，比如利用核技巧、混合建模方法改進文中方法，拓寬算法的適用場合。