地鐵車輪凹形磨耗對輪軌接觸及動力學性能的影響

宦冬，陶功權，謝清林，任德祥，宮彥華，溫澤峰

（1.西南交通大學 牽引動力國家重點實驗室，四川 成都610031；2.軌道交通關鍵零部件安徽省技術創新中心，安徽 馬鞍山243000）

地鐵線路投入運營后，輪軌磨耗不可避免，車輪凹形磨耗（簡稱凹磨）便是其中之一。凹磨是指車輪踏面中部磨耗到低于踏面尾部；車輪在踏面中部形成凹磨后，踏面尾部由于呈凸形像輪緣而稱為假輪緣。凹磨的嚴重程度用踏面凹陷量[1]來評價，其定義為車輪踏面中部最低點與踏面尾部假輪緣處最高點之間的高度差。嚴重的車輪凹磨會影響車輛的運行性能，且輪軌間易產生疲勞損傷，降低車輛的安全性，也增加了車輛與線路的維護成本。因此，研究地鐵車輪凹磨對輪軌接觸關系、車輛動力學性能、輪軌滾動接觸疲勞等的影響，對保證車輛安全運行及制定合理的鏇修策略非常重要。

車輪凹磨改變了車輪踏面原始廓形，使輪軌接觸幾何發生變化，及時進行車輪鏇修可有效改善凹磨帶來的一系列影響，部分學者也基于安全性、經濟性等方面的考慮提出了一些鏇修限值。

貨運鐵路對于車輛、線路的養護往往較差，因此車輪凹磨也較嚴重，在車輪鏇修時凹陷量通常能達到3 mm以上。SAWLEY等[1-2]對北美超過6700個貨車車輪進行測量統計，研究了踏面凹磨的形成及其對輪軌相互作用與直線運行穩定性的影響，指出凹磨會惡化車輛曲線通過性能及對中性能、增大車輛橫向加速度及脫軌風險，提出了凹陷量為3 mm的鏇修限值。LI等[3]基于大秦線重載貨車出現的車輪凹磨和偏磨對車輛動力學行為的影響，建議將凹陷值控制在2 mm之內。FR?HLING等[4]通過對南非重載鐵路的現場觀測以及數值仿真，研究了凹磨對輪軌滾動接觸疲勞的影響，發現車輪凹磨導致輪軌橫向力增大以及接觸斑變窄，進而誘發輪軌疲勞裂紋的萌生與發展，提出了凹陷值為2 mm的鏇修限值。

部分普速客車車輪凹磨也比較嚴重。ALIZADEH等[5]經過大量測試挑選了8個車輪廓形以研究踏面磨耗量和凹陷量對車輛臨界速度的影響，建議將凹陷量列為檢查項目，指出當凹陷值大于2 mm時需及時鏇修。高速列車由于速度快、效率高，更加注重車輛運行安全性與平穩性，因此對車輛維護更嚴格，大多數車輪鏇修時凹陷量在0.3 mm以內。金學松等[6]對某高速鐵路車輪踏面橫向磨耗的特征、機理、影響和對策進行了詳細的闡述，指出高速鐵路由于線路平直度較高，易形成凹磨，凹磨引起輪軌橫向振動，導致軸箱加速度成倍增加以及構架加速度超限，應將磨耗深度控制在0.2 mm之內。CUI等[7]研究了伴隨偏磨的凹磨車輪對車輛系統動力學的影響，綜合考慮運行穩定性、乘坐舒適性、曲線穩定性，提出鏇修閾值。

此外，一些學者研究了車輪凹磨的一系列影響及改進措施。黃照偉等[8]通過動力學仿真建模計算了高速列車車輪凹磨對輪軌接觸幾何特性與車輛系統動力學性能的不利影響。謝清林等[9]分析了某高寒動車組車輪磨耗演變規律，仿真計算車輪凹磨對輪軌接觸特性及車輛運行性能的影響，指出相比于CHN60軌，凹磨車輪與60N軌匹配時車輛體現出更好的服役性能。孫宇等[10]通過車輛軌道耦合動力學理論及改進的KIK-PIOTROWSKI方法研究凹磨對高速動車組輪軌相互作用的影響，結果顯示，凹磨造成的接觸點跳躍能平穩過渡，沒有出現明顯的高頻沖擊現象；凹磨對輪軌垂向力與低頻垂向振動影響不大，但會增加輪軌間高頻垂向振動與輪軌橫向力的振動幅值。趙艷杰等[11]研究了高速動車組踏面與不同鋼軌廓形匹配的影響，指出應優化廓形以改善輪軌接觸集中帶來的車輪凹磨。周志軍等[12]通過有限元方法研究了凹磨對地鐵車輪滾動接觸疲勞的影響，認為凹磨車輪頻繁通過小半徑曲線時易在磨耗突變區造成較高的等效應力和等效塑性應變，導致輪緣根部出現疲勞損傷。SUN等[13]通過建立鋼軌非均勻磨耗預測模型研究了車輪凹磨對鋼軌磨耗的影響，發現嚴重的凹磨會增加鋼軌磨耗寬度，并增加鋼軌磨耗速率。CUI等[14]對武廣線上CRH3型車運營過程中出現的車輪凹磨進行了研究，設計了一種新的車輪型面，能提升磨耗后的動力學性能，并有效減緩凹磨的發展。

目前大量研究更關注于高速列車與貨車車輪凹磨，而對于地鐵車輪凹磨的關注較少。地鐵車輛在結構、編組等方面與高速列車相近，注重運行安全性、平穩性，但地鐵車輛運行速度較低且結構參數存在差異，因此凹磨對于車輛運行性能的影響也有所不同。本文基于某地鐵線路車輪普遍出現凹磨且部分曲線段鋼軌剝離較為嚴重的現象，建立了該線路B型地鐵車輛動力學仿真模型，將實測凹磨車輪與CHN60鋼軌匹配，研究了車輪凹磨對于輪軌接觸幾何關系、車輛動力學性能、輪軌疲勞損傷的影響。

1 車輪磨耗普查測試及其對輪軌接觸幾何關系的影響

1.1 車輪磨耗規律

對某地鐵線路車輪磨耗情況進行普查測試發現，該線路運營車輛車輪磨耗形式主要表現為踏面凹磨，幾乎不存在輪緣磨耗。如圖1所示，在凹磨形成初期，踏面磨耗主要集中在橫向位置-30～30 mm，隨著磨耗深度增大，踏面磨耗范圍逐漸擴大，當凹陷量達到3.2 mm時，踏面磨耗范圍擴展至-37～50 mm。

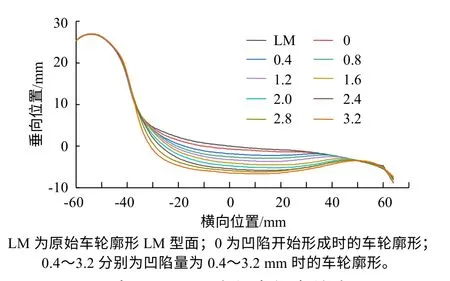
圖1 實測不同凹陷程度的車輪廓形

車輪與鋼軌的接觸點多集中在踏面中部，僅在通過小半徑曲線或道岔時踏面根部與尾部才會與鋼軌接觸，因此踏面磨耗往往在踏面中部較嚴重，而踏面尾部磨耗較少，導致踏面中部下凹而踏面尾部逐漸突起形成假輪緣。如圖2所示，當踏面磨耗量達到1 mm時，踏面凹磨開始逐漸形成，且凹陷量與踏面磨耗量之間呈近似的線性關系，其線性回歸表達式為：

圖2 測試車輪凹陷量與踏面磨耗量的關系

式中：y為凹陷量，mm；x為踏面磨耗量，mm。

1.2 輪軌接觸點對分布

為研究車輪凹磨對輪軌接觸以及車輛動力學性能的影響，選取實測凹陷量為2.38 mm的車輪廓形，根據磨耗規律對其插值得到7個不同磨耗程度的車輪廓形，如圖3、表1所示。由插值得到不同車輪型面的踏面磨耗程度均勻發展，削弱了實測磨耗的隨機誤差，有利于針對性地研究不同嚴重程度凹磨帶來的影響，下文將利用這9個型面進行仿真研究。

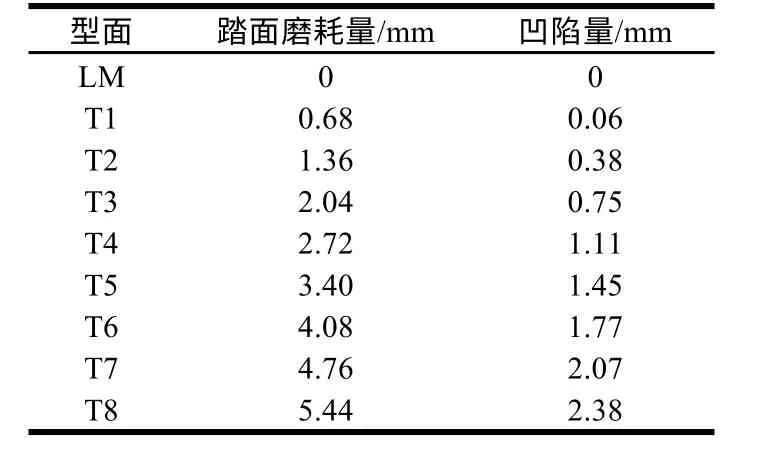
表1 九個型面的踏面磨耗量與凹陷量

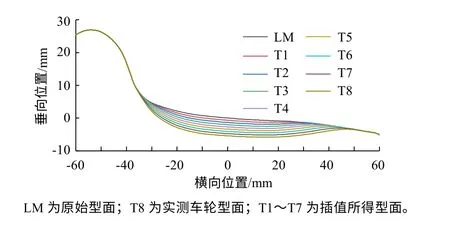
圖3 插值所得車輪廓形

輪軌接觸點位置分布影響車輛動力學性能及輪軌相互作用。將LM型面和T1～T8車輪分別與CHN60軌匹配，在橫移量±12 mm中每隔0.5 mm計算一個接觸點位置。計算中車輪名義滾動圓半徑420 mm，輪對內側距1353 mm，軌距1435 mm，軌底坡1/40。輪軌接觸點對分布如圖4所示，其中鋼軌軌頂中心和車輪名義滾動圓處橫坐標均為零。可知，LM型面與鋼軌匹配時，接觸點對連續分布，而磨耗車輪T1～T8輪軌接觸點對分布分散集中，使車輛在實際運行中輪軌接觸位置易產生橫向跳躍，最終導致輪軌接觸情況惡化。車輪出現凹磨后，輪對發生較小的橫移量便會使輪軌接觸點位置產生較大變動，易使輪軌在軌距角處接觸，增加鋼軌軌距角處發生疲勞損傷的可能性。

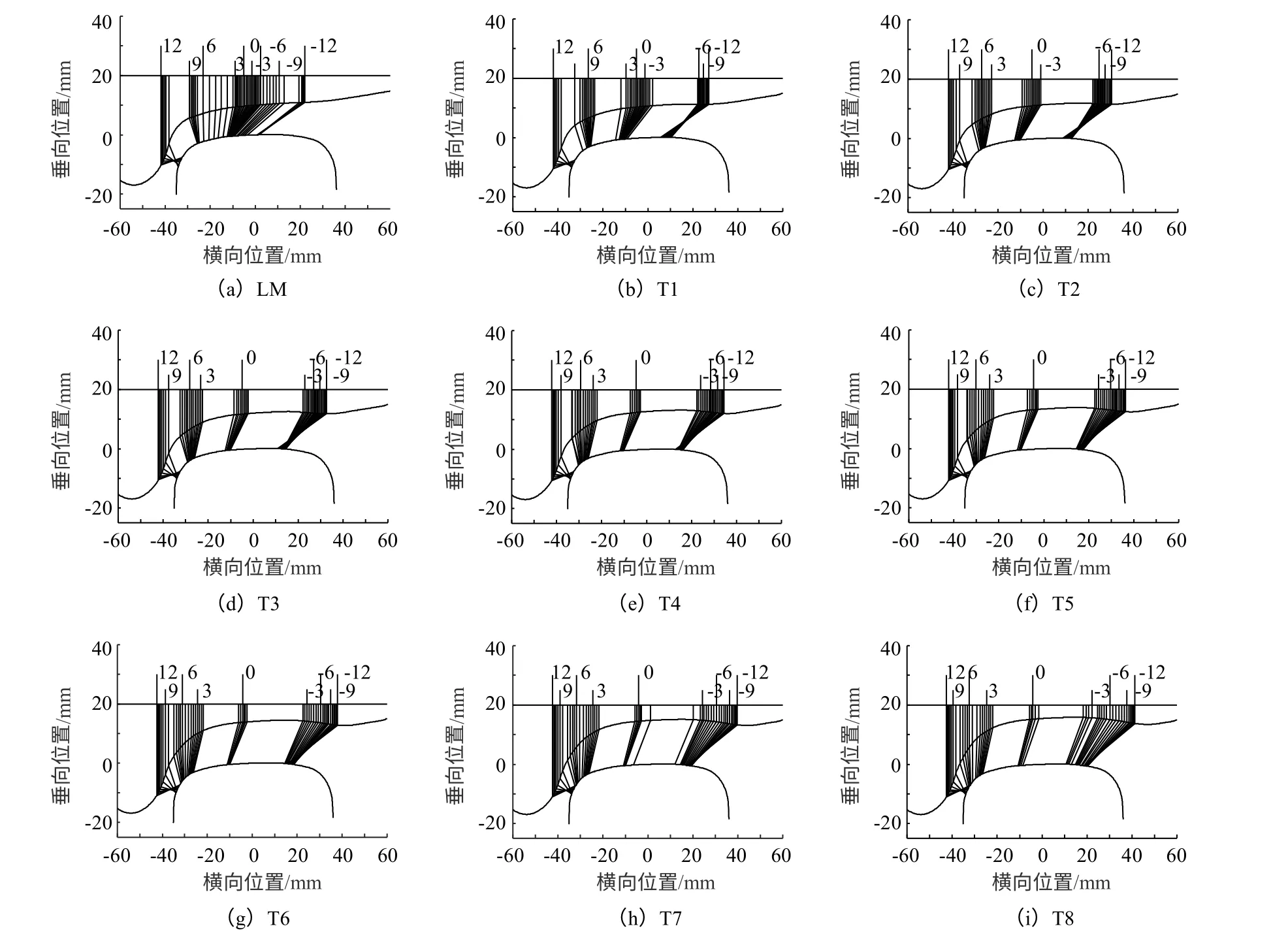
圖4 輪軌接觸點對分布

1.3 滾動圓半徑差

輪對滾動圓半徑差是影響車輛曲線通過性能的重要因素。輪對發生橫移時，滾動圓半徑差越大，越容易以純滾動通過小半徑曲線，不依靠輪緣導向。不同車輪廓形與CHN60軌匹配時在不同輪對橫移量下的滾動圓半徑差如圖5所示，可知，輪對滾動圓半徑差隨車輪凹陷量的增大逐漸增大，且較小的橫移量（2～3 mm）便會獲得較大的滾動圓半徑差（2～4 mm）。

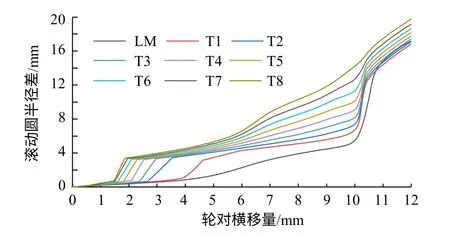
圖5 不同車輪廓形的滾動圓半徑差

1.4 等效錐度

等效錐度是影響車輛蛇行穩定性、曲線通過性能的重要參數。較大的等效錐度可提升輪對對中性能，利于曲線通過，但會降低車輛蛇行穩定性與直線運行穩定性。不同磨耗車輪等效錐度往往存在差異，不同車輪廓形與CHN60軌匹配的等效錐度如圖6所示，采用UIC519積分法計算。可知，隨著車輪磨耗增大，等效錐度逐漸增大，較小的橫移量便能使等效錐度急劇增加并達到極大值，隨后等效錐度減小達到極小值再增加，且凹陷量愈大，此趨勢愈明顯，極值點對應的橫移量愈小。

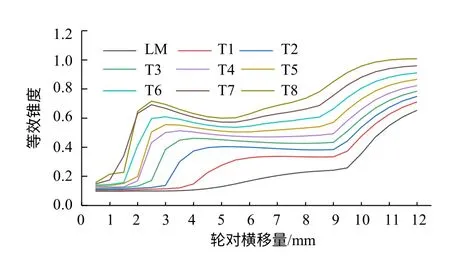
圖6 不同車輪廓形的等效錐度

2 車輪磨耗對車輛動力學性能的影響

2.1 車輛動力學仿真模型

根據某B型地鐵車輛參數，利用多體動力學軟件SIMPACK建立了拖車車輛多體動力學模型，如圖7所示。該模型由1個車體、2個構架、4個輪對和8個軸箱組成，共計15個剛體。車體、構架和輪對均有6個自由度（伸縮、橫移、沉浮、側滾、點頭、搖頭），而軸箱僅保留點頭自由度，共計50個自由度。模型還包含一系橡膠疊簧、二系空氣彈簧、二系橫向減振器、橫向止擋、牽引拉桿。考慮了二系橫向減振器和橫向止擋的非線性特性。本文計算均為重車（AW3）狀態，其主要參數如表2所示。

圖7 車輛動力學模型

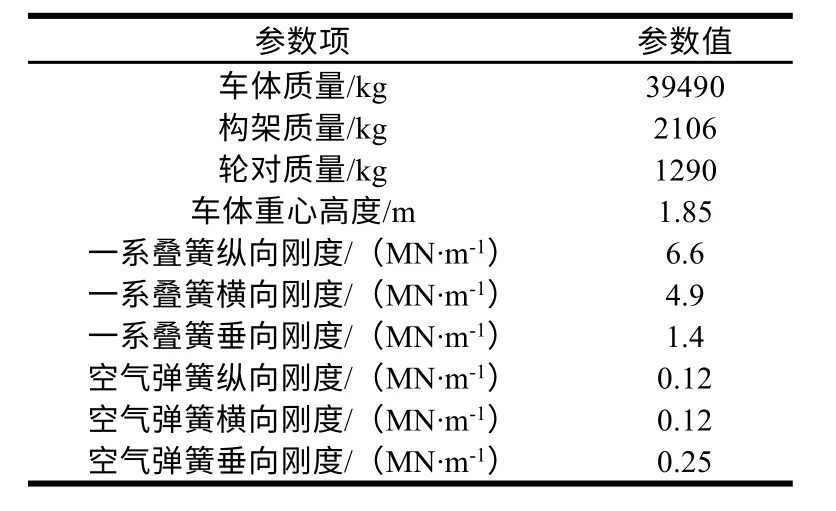
表2 重車（AW3）狀態部分車輛參數

2.2 直線運行性能

車輛直線運行性能主要通過車輛運動穩定性和運行平穩性來評價。

采用非線性臨界速度來評價車輛運動穩定性。通過動力學仿真計算車輛非線性臨界速度時，可以在給定車速下施加初始激擾，觀察車輛運動的收斂情況，剛好不收斂時的速度即為非線性臨界速度；也可采用降速法，在較高速度下施加初始激擾，使車輛發生周期蛇行運動，然后降低車速，車輛運動在某一速度下剛好不收斂（通常情況下認為，輪對橫移量小于0.1 mm時就收斂），即為非線性臨界速度。

本文采用降速法計算車輛非線性臨界速度。首先在線路上給定一段軌道不平順，激發車輛的蛇行運動，然后運行到一段無激擾的線路上，車輛施加0.5 m/s2的減速度，通過一位輪對橫移量是否收斂來判斷車輛非線性臨界速度。如圖8所示，隨著磨耗增大，車輛非線性臨界速度逐漸減小。磨耗輪T8的臨界速度最小，為112 km/h。車輪出現磨耗后，等效錐度的增大是導致臨界速度下降的主要原因。

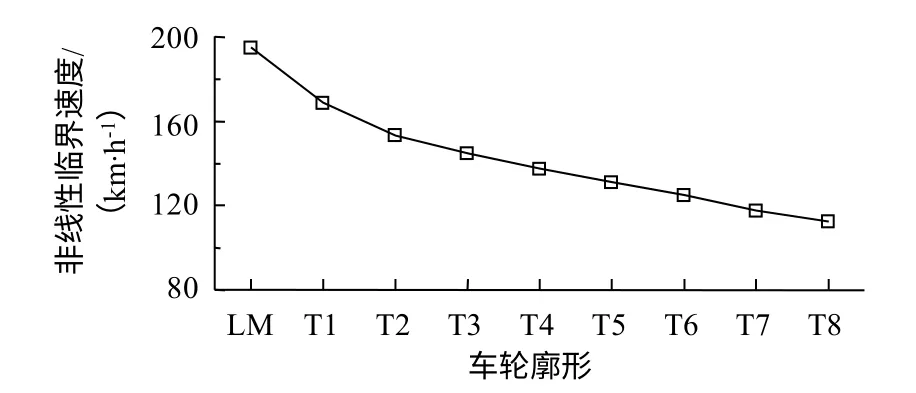
圖8 車輛在不同車輪廓形下的非線性臨界速度

運行平穩性主要反映車體振動狀態及其對客車上旅客乘坐的影響。根據GB/T 5599－2019[15]中有關規定及Sperling相關公式計算車輛的垂向、橫向平穩性指標。

由GB/T 5599－2019可知，平穩性指標W≤2.5為1級，評定為優。圖9施加的軌道不平順為美國五級譜，由圖可知，車輪LM～T8平穩性指標均為優。車輪凹磨對車輛垂向平穩性幾乎沒有影響，但對橫向平穩性的影響略為敏感。隨著磨耗增大，車輛橫向平穩性反而變好。

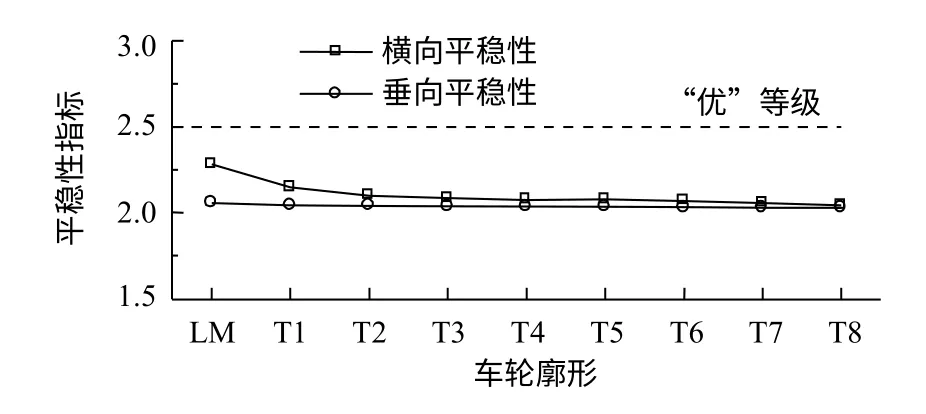
圖9 車輛以75 km/h速度運行時的平穩性指標

圖10給出了車輪分別為LM以及T1、T8型面時的平穩性測量點處車體橫向加速度頻譜圖。平穩性指標主要由車體振動加速度幅值及頻率決定，由Sperling相關公式計算的車輛橫向平穩性指標在0.5～10 Hz頻率范圍加權較大，加權最大頻率在5 Hz左右。車輪出現磨耗后，等效錐度增大，輪對和構架橫向振動加劇，但構架橫向振動經過空氣彈簧以及二系橫向減振器的衰減，對車體橫向振動影響較小。由圖10可知，相較于原始車輪型面，T1、T8磨耗型面車體橫向振動加速度在1～2 Hz和4.5 Hz附近有所減小，導致橫向平穩性指標減小。對比于原始型面，磨耗型面滾動圓半徑差較大，使車輛在橫向激擾下能快速對中，減少了車輛橫向晃動，提升了車輛運行平穩性。在該線路車輪鏇修前后的車輛振動測試中也發現，較多區間車輛橫向平穩性指標在車輪鏇修后反而比鏇修前要高，車輪由凹磨型面恢復到標準LM型面并未提升車輛橫向平穩性，反而有所降低，仿真結果與測試結果具有相同的規律。

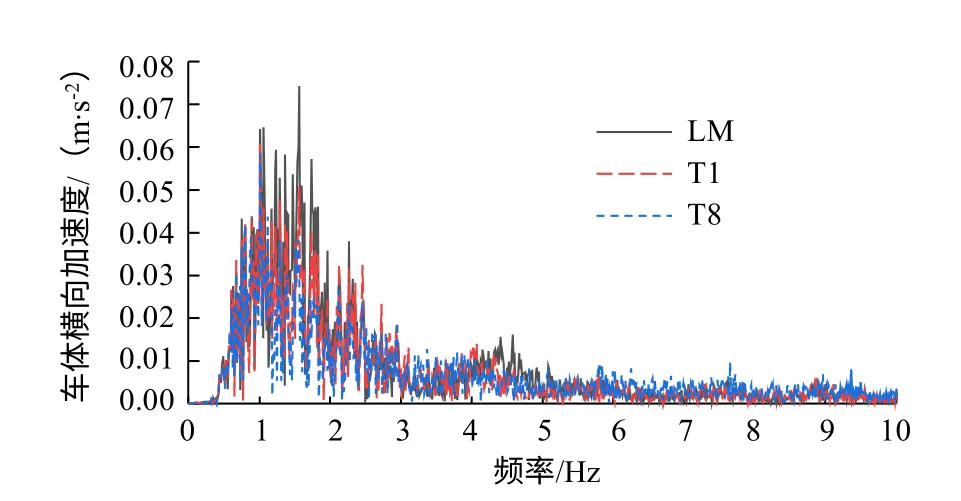
圖10 橫向加速度頻譜圖

2.3 曲線通過性能

車輛曲線通過性能主要通過輪軌垂向力、輪軸橫向力、脫軌系數和輪重減載率來評價。

根據GB 50157－2013[16]，設置不同半徑曲線的緩和曲線長度、超高以及車輛曲線通過速度，各曲線工況如表3所示。計算車輛曲線通過性能時不考慮軌道不平順。

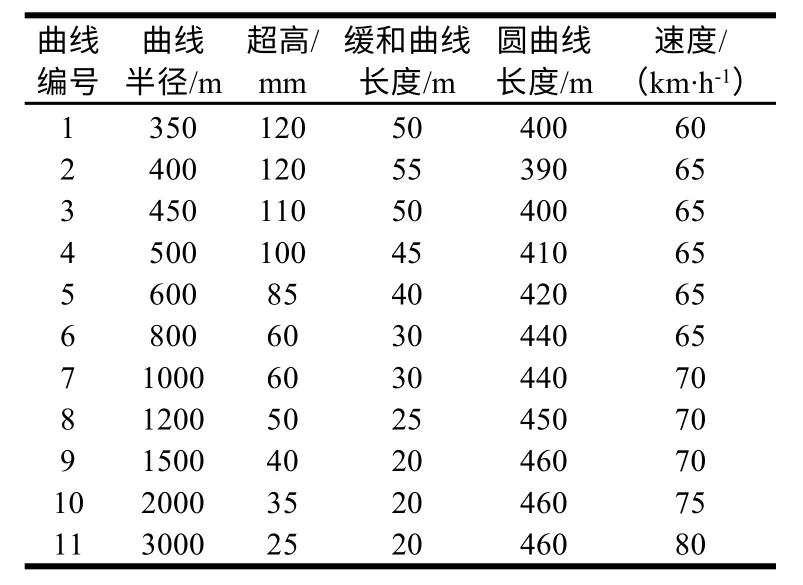
表3 曲線通過線路設置

車輛通過曲線時，輪對沖角越小，說明輪對以更接近純滾動的姿態通過曲線。沖角越大，則會增大橫向蠕滑力，進而增大輪軌磨耗；當發生輪緣貼靠時，則會加劇輪緣磨損與鋼軌側磨。由圖11可知，車輛通過曲線半徑越小時輪對沖角越大，車輪磨耗對沖角影響較小。

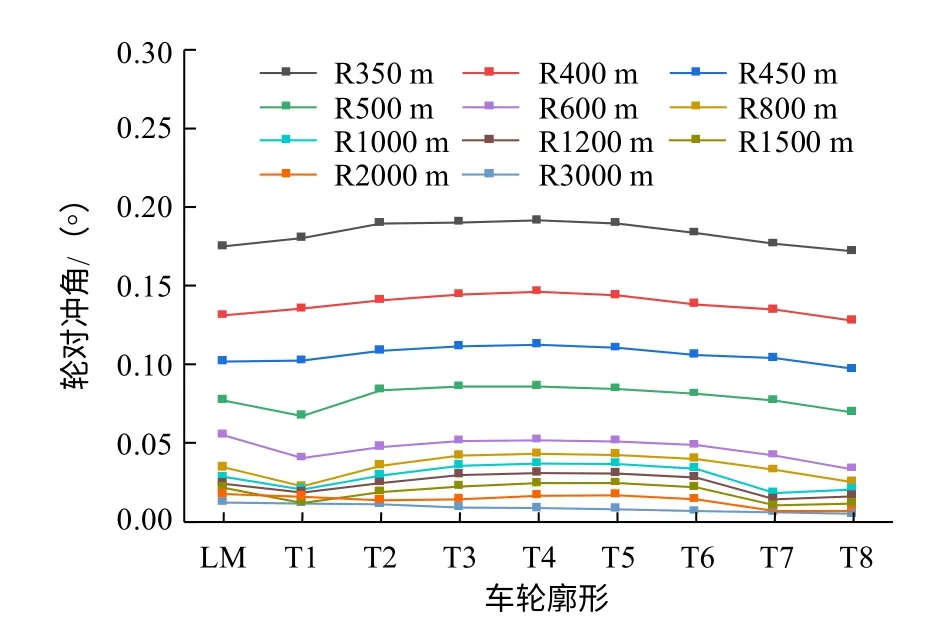
圖11 車輛通過曲線時的一位輪對沖角

輪軸橫向力影響車輛曲線通過的安全性。過大的橫向力會增加脫軌風險、導致軌距擴寬或線路產生變形。根據GB/T 5599－2019，輪軸橫向力應滿足：

式中：H為輪軸橫向力，kN；P0為靜軸重，kN。

計算中，靜軸重約114.6 kN，因此輪軸橫向力應小于53.2 kN。由圖12可知，不同凹陷量的車輪輪軸橫向力均滿足規定。車輛在通過小半徑曲線時，隨著磨耗增加，最大輪軸橫向力減小；通過大半徑曲線時，輪軸橫向力幾乎不變。這是由于隨著車輪凹陷量的增大，車輛通過曲線時獲得的滾動圓半徑差變大，有利于車輛通過小半徑曲線，減少輪緣貼靠，從而使輪軸橫向力減小。

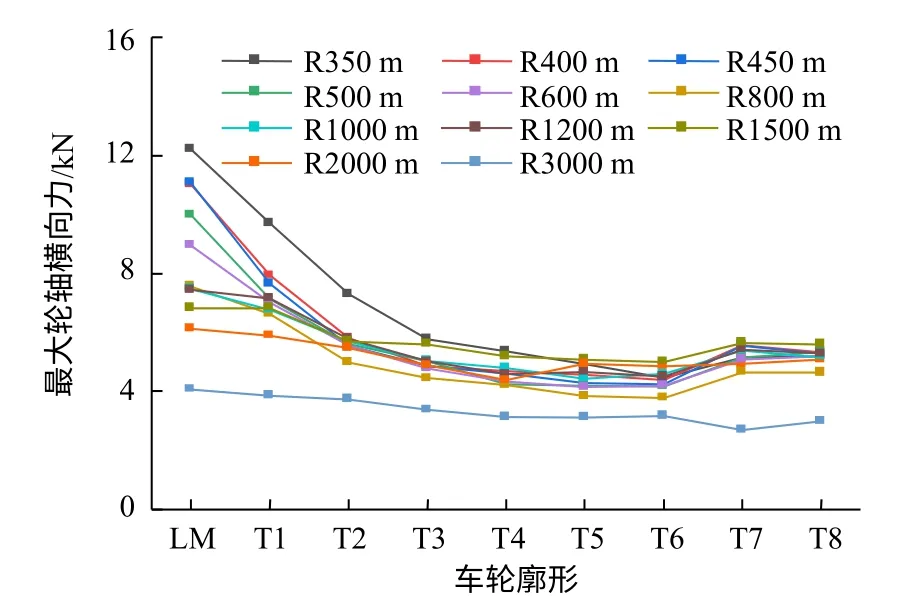
圖12 車輛通過曲線時的最大輪軸橫向力

脫軌系數是評價車輛通過曲線安全性的重要指標。GB/T 5599－2019規定，曲線半徑R在250～400 m時，客車脫軌系數應小于等于1.0，其他線路（曲線半徑R＞400 m）應小于等于0.8。由圖13可知，脫軌系數均在安全范圍內。車輛通過曲線半徑越小，脫軌系數越大。在通過小半徑曲線時，凹磨車輪相較于LM型面脫軌系數更小，這是由于磨耗車輪滾動圓半徑差較大、車輪通過曲線時輪對橫移量減小、輪軌橫向力減小、而輪軌垂向力基本不變。

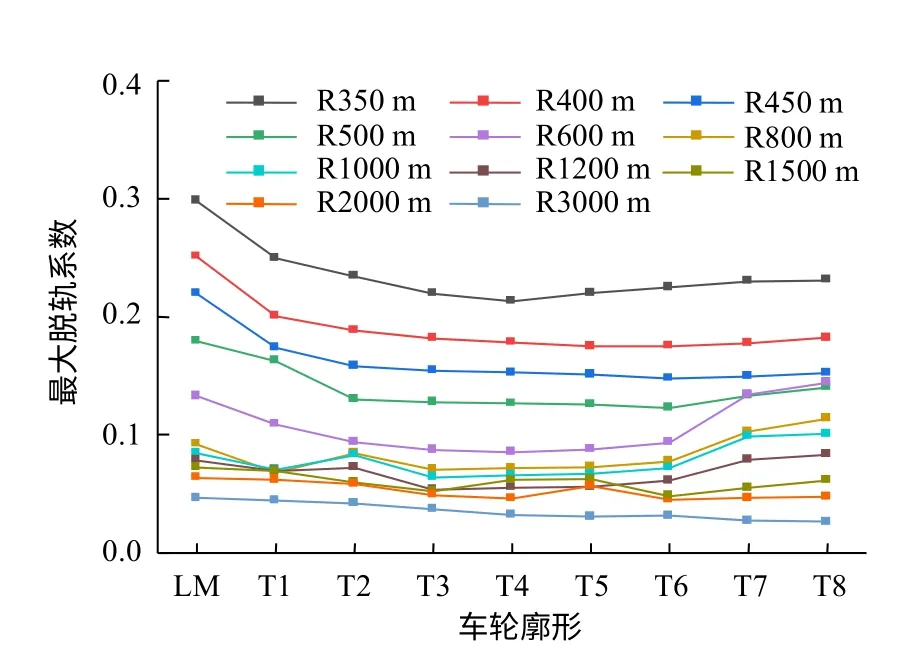
圖13 車輛通過曲線時的最大脫軌系數

輪重減載率也是評價車輛通過曲線時安全性的一個重要指標，防止輪重減載過大而引起脫軌。通過計算發現，車輪凹磨對輪重減載率幾乎沒有影響。

3 車輪磨耗對輪軌接觸疲勞的影響

輪軌表面材料產生棘輪效應和低周疲勞是輪軌表面裂紋萌生的主要原因。采用EKBERG等[17]提出的基于安定圖的表面疲勞指數來評價輪軌滾動接觸疲勞特性，其定義為：

式中：surfFI為表面疲勞指數（surface-initiated Fatigue Index）；a和b分別為橢圓接觸斑的長半軸和短半軸；k為材料純剪切屈服強度，取355 MPa；Fz為輪軌法向力，N；μ為牽引系數；Tx和Ty分別為輪軌縱向和橫向蠕滑力，N。

如果計算得到的FIsurf為正值，則可能產生滾動接觸疲勞。

圖14為車輛以60 km/h的速度通過曲線半徑350 m（表3曲線編號1）時的導向輪對車輪表面疲勞指數隨運行距離變化圖，計算時不考慮軌道不平順的影響。由圖可知，車輛在曲線段時，車輪表面易形成疲勞裂紋，且高軌側車輪表面疲勞指數普遍大于低軌側，這是由于高軌側車輪牽引系數更大而接觸斑面積更小。在緩和曲線段，磨耗較大的車輪表面疲勞指數存在較大波動，這是由于此時車輛剛剛進入緩和曲線，輪軌之間出現接觸點跳躍或兩點接觸。對于圓曲線段，高軌側車輪原始型面的表面疲勞指數大于0，低軌側小于0，車輪踏面磨耗出現凹陷后，兩側車輪表面疲勞指數均增大且大于0，但大小相差不大，說明車輪磨耗之后輪軌接觸點處易萌生疲勞裂紋。

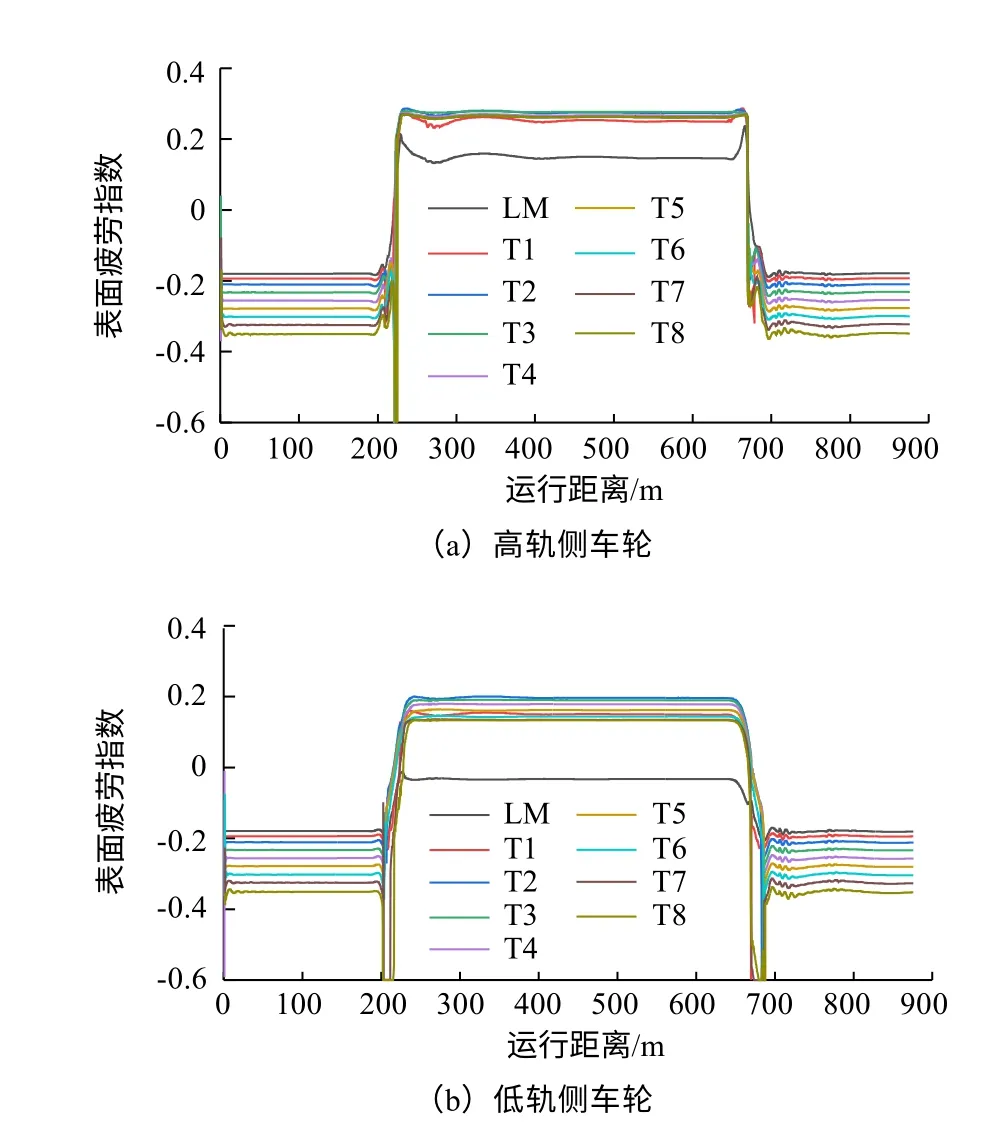
圖14 導向輪對車輪表面疲勞指數

圖15為車輛通過該曲線時兩側車輪的最大Hertz接觸壓力，計算公式為：

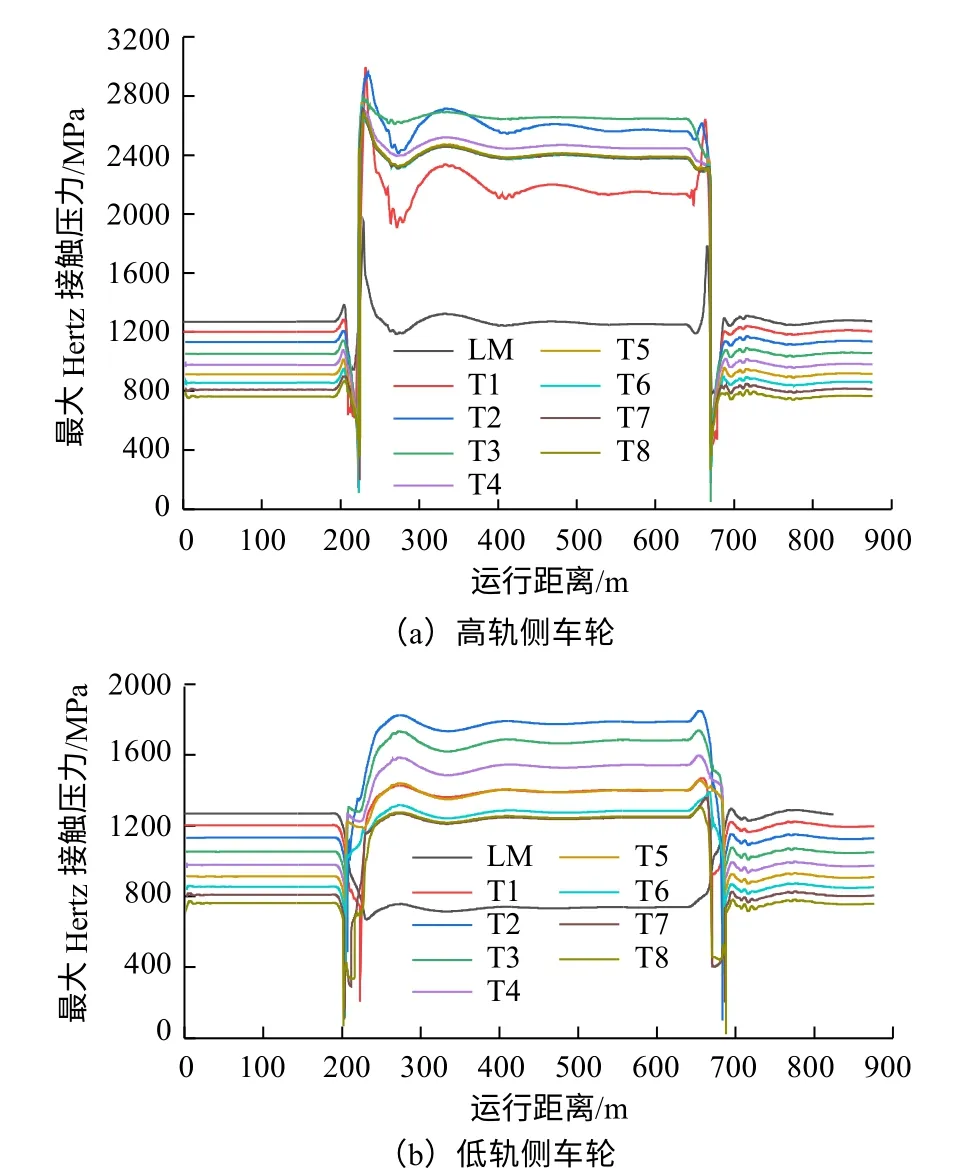
圖15 導向輪對最大接觸壓力

由式（3）和式（5）可知，最大Hertz接觸壓力的變化會引起表面疲勞指數變化。車輪磨耗對牽引系數的影響較小，在曲線段時，高軌側牽引系數在0.39左右，而低軌側在0.37左右，因此接觸斑內接觸壓力的增大是車輪表面疲勞指數增大的主要因素。

由圖15可知，車輪磨耗后最大Hertz接觸壓力急劇增大，且高軌側大于低軌側。隨著磨耗發展，低軌側車輪的接觸壓力呈現先增大后減小的趨勢，這是由于在凹磨形成初期，踏面磨耗寬度較小，假輪緣在20～30 mm處，車輛通過曲線時輪對橫移量較大（10 mm左右），低軌側在假輪緣處接觸，導致接觸斑小而接觸壓力大；隨著磨耗寬度不斷加大，假輪緣往踏面尾部移動，且由于滾動圓半徑差增大，車輛通過曲線時輪對橫移量減小（6 mm左右），因此接觸點在假輪緣內側，接觸斑較大，接觸壓力小。而在直線段，由于車輪磨耗使車輪廓形向著輪軌共形接觸趨勢發展，因此隨著車輪磨耗，接觸斑面積逐漸增大而接觸壓力逐漸減小。

針對表3所列曲線，當半徑小于等于500 m時，車輪表面疲勞指數及最大Hertz接觸壓力與上述350 m半徑曲線相似。在半徑為3000 m的曲線段與直線段上計算結果差異較小。對于半徑600～2000 m的曲線，高軌側車輪輪緣根部與鋼軌軌距角處的接觸斑較小，接觸壓力較大，易產生輪軌滾動接觸疲勞，曲線低軌側車輪表面疲勞指數小于0，不易產生疲勞；標準LM型面則在高低軌側均不易產生疲勞。

4 結論

凹磨的發展造成了以下影響：

（1）磨耗寬度逐漸變大，且接觸點對由均勻分布變為集中到踏面中部、輪緣根部、假輪緣內側三個獨立區域。

（2）滾動圓半徑差以及等效錐度增大，車輛的臨界速度降低，但車輛曲線通過性能提升。針對本文研究的地鐵車輛，凹磨對車輛垂向穩定性幾乎沒有影響，會提升車輛橫向穩定性。

（3）車輛通過R≤2000 m曲線時，高軌側車輪易在輪緣根部與鋼軌軌距角接觸，接觸斑窄而接觸壓力大，易產生輪軌滾動接觸疲勞；車輛通過R≤500 m曲線時，低軌側車輪假輪緣內側與鋼軌軌頂外側接觸，易在假輪緣處和軌頂外側產生滾動接觸疲勞。