讓評價的過程成為學習的過程
——以小學數學紙筆測試命題設計為例

浙江省杭州市江干區教育發展研究院 潘紅娟

紙筆測試作為學生學業評價的重要途徑，被廣大教育工作者持續關注與深度研究。數學命題設計要“關注數學本質”“指向學習過程”“突出素養立意”“尊重學生差異”等理念已逐漸成為共識。但是，如何發掘紙筆測試中的“學習”功能，將評價的過程視為“學習”的過程，則鮮有人研究。

筆者已有二十余年的命題實踐經驗，評價不僅具有導向、診斷、激勵的功能，同樣，也具有“學習”的功能。為什么？首先，試題本身可以作為“信息源”，向學生傳遞數學常識、數學文化、時事信息、多元方法；其次，解題過程可以作為“方法源”，讓學生體驗問題解決的不同思路與策略，感受不同的數學思想方法；最后，解題結果可以得到“新命題”，獲得一些新的規律、定律、性質、公理等結論。因而，好的命題設計，不僅指向于考查目標的有效達成，同時，可以在拓寬知識視野、完善認知結構、豐富學習經驗、提升學習智慧等方面有所作為。

下面，以小學數學紙筆測試命題設計為例，從優化方法的習得、數學文化的滲透、后續學習的孕伏、思想方法的滲透、數學新規律的發現、非常規問題的探索、現實世界的關注等維度展開分析。

一、試題指向優化方法的習得

考試雖指向于學習結果的評測，但如果能在試題中有意識地融入解決問題的優化思路，讓學生在解題過程中感知不同方法、體驗優化思想，并在之后類似問題的解決中得以有效遷移，則顯然是對考試功能的再拓展。

【試題舉例】計算4÷4.4，根據圖1中的筆算過程，下列結果正確且最簡潔的是（ ）。

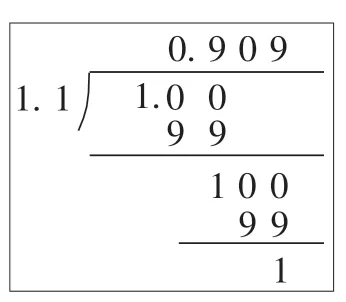
圖1

【分析】此試題考查目標指向于“循環小數”的算理理解，旨在考查學生是否理解“商的循環出現，其原因是余數的循環出現”之本質，要求學生根據余數的重復出現判斷商的循環節。同時，試題將“4÷4.4”轉化為“1÷1.1”進行筆算，顯然，意在向學生示范“根據商不變性質自覺轉化，簡便計算”的思路與方法，運算能力中“能根據數據特征靈活運算”這一目標蘊含其中。

【試題舉例】

【分析】兩題均是六年級“分數乘除”內容的試題。題①綜合考查“運算定律在分數計算中的運用”“求一個數的倒數”等相關知識。同時，試題又給出“如何通過轉化將復雜計算變得簡單”這一思路提示，幫助學生積累一種靈活計算的策略，使其在今后同類運算中得以運用。題②，同樣出于這一命題理念，幫助學生積累優化策略的同時，對“分數除法”與“整數除法”做了算理算法上的聯系與溝通。

二、試題指向數學文化的滲透

結合相關內容進行“數學與現實生活”“數學與科學技術”“數學與人文藝術”“數學史”等數學文化的滲透，在教學中已被充分關注。事實上，考試評價同樣可以將數學文化的滲透融入其中。例如，可以根據數學史、數學名題、歷史材料編制數學試題，實現考查目標的同時，讓學生了解數學之史、領略數學之美、感受數學之用。

【試題舉例】“哥德巴赫猜想”認為，所有大于2的偶數，都可以表示為兩個質數的和。如6=3+3，8=5+3，10=7+3，12=7+5，14=11+3……請你將60寫成兩個質數之和：60=（ ）+（ ）=（ ）+（ ）。

【分析】試題指向于“質數”概念的考查，并不要求學生記憶概念語言，而是基于概念理解進行舉例，這樣的命題，體現對數學概念本質的考查。我們也看到，題干給出“哥德巴赫猜想”的背景介紹，意在拓寬數學視野，了解數學家與數學名題。考查概念的同時，學習已無痕發生。

【試題舉例】

①圖2中有六個小正方形，它們的邊長是一組斐波那契數列，分別是：1，1，2，3，5，8，用這些數作半徑，可畫出美妙的螺旋線。

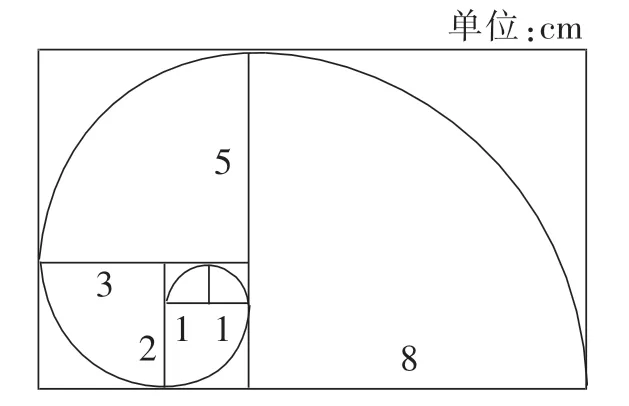
圖2

請計算圖中螺旋線的長度是（ ）cm。（結果可用含有π的式子表示）

②如果要計算12+12+22+32+52+82，有什么簡便的方法呢？我們可以用“數形結合”的方法來研究。觀察圖2和下面的算式，填空：

12+12=1×2

12+12+22=2×3

12+12+22+32=（ ）×（ ）

12+12+22+32+52+82=（ ）×（ ）=（ ）

【分析】將經典的“斐波那契數列”作為試題素材，考查圓的周長、數與形兩個知識點，這樣的命題，情境新穎，知識綜合。題①需要判斷螺旋線每段弧長的圓心、半徑，然后計算周長。題②一方面考查學生用“式”表達“形”的能力，另一方面考查學生借助“形”探究“式”的規律，以數解形、以形助數的思路凸顯。當然，試題并不滿足于此，而是試圖向學生打開數學文化的窗口，領略斐波那契數列的神奇，感受數列螺旋線的美妙。考查結束，還可以將這一內容作為長周期作業，布置學生搜索“斐波那契數列還有哪些奇妙的結論”“美妙的螺旋線在生活中有哪些應用”等，相信會是一次美妙的數學文化之旅。

三、試題指向后續學習的孕伏

試題若能既著眼當前，有效測查知識能力的掌握情況，又能為后續學習積累相應的經驗，則能發揮最大功效。后續學習的鋪墊與孕伏，可以是知識層面的，也可以是方法層面的。

【例題舉例】由圖3中的數據可知，兩條直角邊的長度（ ）。

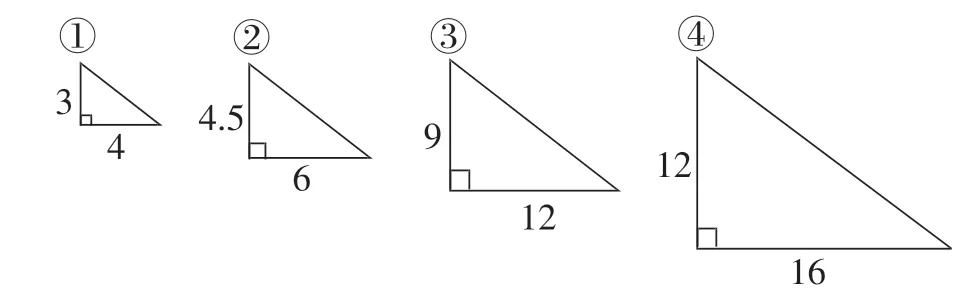
圖3

A.不成比例關系

B.成正比例關系

C.成反比例關系

【分析】試題考查對正反比例意義的理解，難度不大，但很好地突破了形式判斷的記憶水平，要求學生真正理解正比例“一個量變化，另一個量隨之變化”“相對應的量比值一定”，針對這一本質內涵進行概念辨析。試題給出的是一組相似三角形，為初中相似圖形、相似多邊形對應邊成比例、比例線段等知識的學習，做了很好的孕伏。

【試題舉例】圖4中，a、b、c、d、e是五條等距的平行線，線段AD和BC相交于b直線上的E點。已知線段AB=4cm，AB∶CD=1∶3，△ABE的面積為4cm2，△CDE的面積是（ ）cm2。

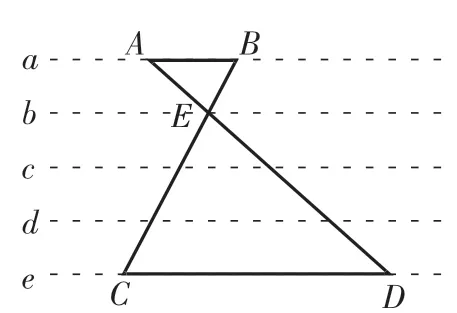
圖4

【分析】本題指向比例應用的綜合考查，基本思路為：根據“1∶3”求出CD；根據兩個三角形高的關系求出△CDE的高；底與高均已知，則可以求得△CDE的面積。在考查學生能否利用比例知識解決變式問題的同時，為初中學習相似三角形的面積比等于相似比的平方做了有效鋪墊。

四、試題指向思想方法的滲透

能否在命題設計時，將數學思想方法蘊含其中，需要命題者突破知識技能的考查視野，具有高瞻遠矚的戰略眼光。

1.恒等思想

【試題舉例】如圖5，有大小兩個圓，將兩個圓如圖6放置，陰影部分面積是（ ）cm2；如圖7放置，陰影面積是（ ）cm2；如圖8放置，兩塊陰影面積的差是（ ）cm2。

圖5

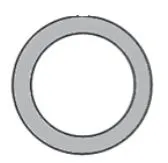
圖6

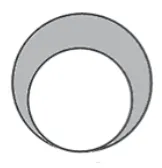
圖7

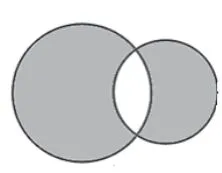
圖8

【分析】此題考查內容為圓環面積。圖6、圖7著眼于基本方法的掌握，圖8則給出一個非常規圖形，不同層次的學生可以有不同的解題策略。水平較低的學生可以假設空白部分的面積，再計算求得；水平較高的學生可利用等式性質，得到“（S大圓-S空白）-（S小圓-S空白）=S大圓-S小圓”，推理獲得結論。考查圓環面積的同時，將恒等思想孕伏其中。

2.簡化思想

【試題舉例】一批圓柱形茶葉罐的規格是：底面直徑8厘米，高12.5厘米。新茶上市了，茶葉公司用這批茶葉罐裝新茶，并采用如圖9的包裝方法進行包裝。問：裝入茶葉罐后，長方體盒子內剩余的空間占長方體盒子容積的百分之幾？（π取3.14）

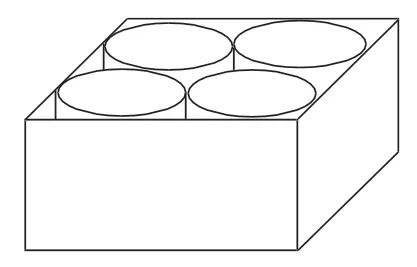
圖9

【分析】命題設計將“簡化思想”的考查蘊含其中。方法一：先求出長方體盒子內剩余體積及長方體盒子容積，再求百分率；方法二：從“體”的關系轉化為“面”的關系，再求百分率；方法三：將四個單位轉化為一個單位計算，求出一個茶葉罐的空余體積與所占長方體的體積之間的百分率；方法四：簡化為“一個茶葉罐底面的空余面積與所占長方體的底面面積之間的百分率”等。顯然，方法二、三、四中思維的靈活性、問題的簡化能力明顯高于方法一。

3.化歸思想

【試題舉例】圖10中，正方形ABCD的邊長是5cm，正方形CEFG的邊長是3cm，求陰影部分的面積。

①小明解決這個問題的計劃是：

陰影部分的面積=四邊形BEFD的面積-三角形BEF的面積

四邊形BEFD的面積=三角形BCD的面積+（ ）的面積

解答：

②小強解決這個問題的計劃是：

如圖11，因為BD與CF平行，所以三角形BDF（陰影部分）和三角形（ ）同底等高。因此，求陰影三角形的面積就是求三角形（ ）的面積。

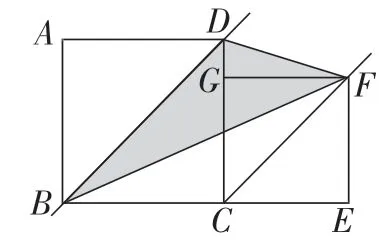
圖11

解答：

③如果正方形ABCD的邊長不變，將小正方形CEFG改為邊長為1cm的正方形，如圖12，請比較圖10、圖12中陰影部分的面積大小，并說明理由。

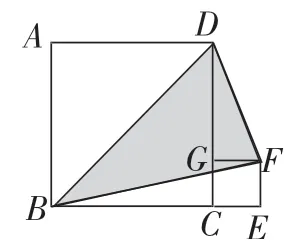
圖12

【分析】化歸，是指在解決問題時，將待解決的問題甲，通過某種轉化，歸結為一個已經解決或者比較容易解決的問題乙，然后通過乙問題的解決返回去得到問題甲的解決。此試題正是考查學生能否將復雜圖形化為簡單圖形的能力，題①是將復雜圖形化為簡單圖形的加減，題②、題③則是引導學生將陰影三角形通過等積變形，轉化為直角三角形BDC的面積來解決。試題試圖幫助學生體會“化歸”的基本思想，并促進方法策略的形成，從而提高靈活解決問題的能力。

4.極限思想

【試題舉例】不計算，用發現的規律直接寫出下面算式的商。

那么7÷11=（ ），11÷11=（ ），12÷11=（ ）。

【分析】此題為“用計算器探索規律”的內容，考查學生能否通過觀察、推理，找到商的變化規律。我們看到，根據規律可得，基于已有經驗可知這一極限思想得以隨機滲透。

五、試題指向新規律的發現

對學生進行知識能力評測的同時，很多時候，還能通過解題過程與解題結果，幫助學生獲得一個新的規律、新的結論，這樣的試題，可謂獨具匠心，令人回味無窮。

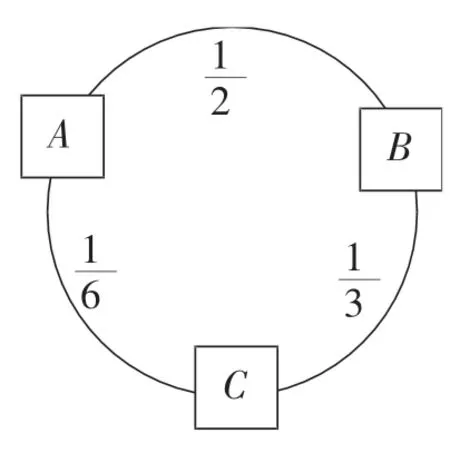
圖13

【分析】本題意在考查學生對分數加減計算的掌握情況，如果學生能分別求出A、B、C的值，然后正確求得圓上所有數的和，則達到考查目的。試題也為優秀學生預留了“先發現規律然后計算”的空間，希望學生可以發現，圓上所有數的和，其實是三個數重復加了3次，這樣，則可以得出“和=原數和的3倍”這一新結論。

【試題舉例】有A、B、C三個數，如果數A除以5，余數是3；數B除以5，余數也是3，數C除以5，余數是2。且A＞B＞C。

小明認為：A與C的和一定是5的倍數。

小紅認為：A與B的差也一定是5的倍數。

他們兩人的說法是否正確？請說明你的觀點和理由。

【分析】人教版數學“因數倍數”單元中，“奇偶性”例題指向于“將抽象問題轉化為具體問題來解決”，此題正是對這一問題解決能力的考查，學生可通過列舉、推算等方式完成觀點說理，學生由此也獲得了“同余問題”的新結論。

六、試題指向于非常規問題的探索

這里所指的非常規問題，是指運用學生現有的知識基礎與經驗儲備難以完成的問題。這樣的試題，如若能給出一個自學提示，根據問題之間的聯系，促進學生對解決方法的類比與遷移，則能實現“自學能力考查”與“非常規問題思路學習”的雙重目的。

【試題舉例】我們曾經用圖14中的方法解決了求三角形面積的問題，用這樣的經驗，你能求出圖15這個幾何體的體積嗎？（單位：cm）

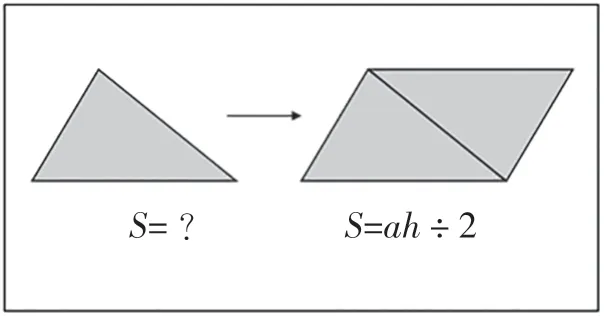
圖14

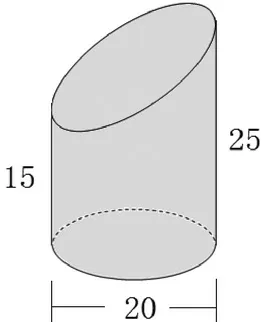
圖15

【試題舉例】圖16中，若圓柱和圓錐等底等高，則圓錐體積是圓柱體積的圖17 中，若這個四棱錐的底和高與長方體的底和高分別相等，則四棱錐的體積是（ ）。（單位：cm）

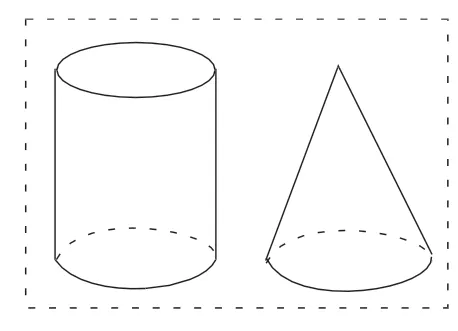
圖16

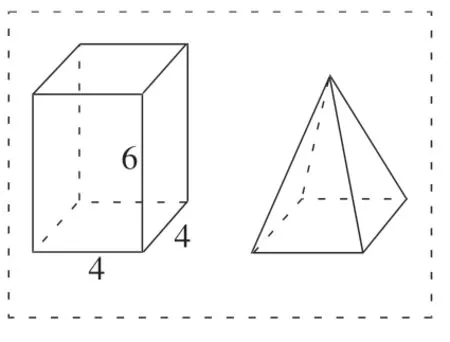
圖17

【分析】這兩道題，非規則幾何體與四棱柱的體積都是學生沒有學過的內容，試題給出“圖形轉化”的思路提示、“圓柱與圓錐”的關系提示，引導學生通過類比推理，找到解決的思路與方法。可以說，這兩題是學習功能試題的典型例證。

七、試題指向現實世界的關注與解釋

會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界，是新課標提出的數學核心素養的具體內涵。評價如何凸顯對現實世界的觀察、思考與解釋，是命題者需要關注的重要方面。

【試題舉例】“一元錢去哪了”的小故事。

小明向爸爸媽媽各借錢50元，買書用了97元，剩下的錢，各還父母一元，還欠父母各49元，自己還剩下1元。他算了一下：49元+49元=98元，98元+1元=99元。小明覺得很奇怪，還有一元去哪了？

你覺得小明錯哪了？根據這個故事情境，請你寫出兩個正確的等量關系：

向父親借的錢+向母親借的錢=（ ）

欠父親49元+欠母親49元=（ ）

【分析】試題期待學生尋找情境中正確的數量關系，解釋“一元錢去哪兒了”的疑惑，一方面，指向學生“關系表征”的能力考查；另一方面，將視角從單純的數學題中走出來，轉向現實世界，引導學生關注生活，并用數學語言解釋、表達現實。

最后，值得說明的是，試題作為一個測量單元，它有刺激情景和對應答形式的規定，它的目的是獲得被試的應答，并根據應答對考生的某些心理特質方面的表現（如知識、能力等）進行推測。命制一道試題，需要回答“考什么能力”“考什么內容”“用什么材料考”“用什么方式考”“問什么問題”“怎么回答”“怎樣賦分”“難度預估”等相關問題。因而，本文所提出的“試題要具有學習功能”，應該是在保證試題信度、效度基礎上的增值思考，與同行探討！