基于差分修正的SGDM算法①

袁 煒,胡 飛

(天津大學 數學學院,天津 300350)

當前,深度神經網絡模型在視覺[1]、文本[2]和語音[3]等任務上都有著非常好的表現.但是隨著神經網絡層數的加深,模型的訓練變得越來越困難.因此,研究人員開始關注優化方法.隨機梯度下降法(SGD)是求解優化問題的一種簡單有效的方法,SGD 被廣泛應用于實際問題[4].該方法根據小批量(mini-batch)樣本的可微損失函數的負梯度方向對模型參數進行更新,SGD具有訓練速度快、精度高的優點.但由于其參數是每次按照一個小批量樣本更新的,因此如果每個小批量樣本的特性差異較大,更新方向可能會發生較大的變化,這導致了它不能快速收斂到最優解的問題.因此,SGD有很多變種,一般可以分為兩類.第一類是學習率非自適應性方法,使用梯度的一階矩估計——SGDM[5],結合每個小批量樣本的梯度求滑動平均值來更新參數,極大地解決了SGD 算法收斂速度慢的問題,這個方法目前應用非常廣泛,本文就針對這個方法進行改進.第二類是學習率自適應性方法,利用梯度的二階矩估計實現學習率的自適應調整,包括AdaGrad[6],RMSProp[7],AdaDelta[8],Adam[9].其中Adam是深度學習中最常見的優化算法,雖然Adam 在訓練集上的收斂速度相對較快,但在訓練集上的收斂精度往往不如非自適應性優化方法SGDM,且泛化能力不如SGDM.AmsGrad[10]是對Adam的一個重要改進,但是最近的研究表明,它并沒有改變自適應優化方法的缺點,實際效果也沒有太大改善.RAdam[11]是Adam的一個新變體,可以自適應的糾正自適應學習率的變化.

目前很多研究都集中在第二類學習率自適應性方法上,卻忽略了最基本的問題.無論自適應還是非自適應方法都用了指數滑動平均法,這些方法都試圖用指數滑動平均得到近似樣本總體的梯度,然而這種方法是有偏且具有滯后性的.針對這一問題我們提出了RSGDM算法,我們的方法計算梯度的差分,即計算當前迭代梯度與上一次迭代梯度的差,相當于梯度的變化量,我們在每次迭代時使用指數滑動平均估計當前梯度的變化量,然后用這一項與當前梯度的估計值進行加權求和,這樣的做法可以降低偏差且緩解滯后性.

1 RSGDM 算法

算法1.RSGDM 算法:所有向量計算都是對應元素計算輸入:學習率,指數衰減率,隨機目標函數α β f(θ)隨機初始化參數向量,初始化參數向量,初始化時間步長θt θ0m0=0,z0=0,?g1=0 t=0 While 不收斂 do t←t+1計算t 時間步長上隨機目標函數的梯度:gt←?θ ft(θt?1)計算差分:?gt=gt?gt?1更新梯度和差分的一階矩估計:mt←β?mt?1+(1?β)?gt zt←β?zt?1+(1?β)??gt用差分的一階矩估計修正對梯度的估計:nt←mt+β?zt更新參數:θt←θt?1?α?nt end Wimages/BZ_225_290_2831_291_2833.pnghile θt輸出:結果參數

算法1 展示了RSGDM 算法的整體流程.設f(θ)為關于θ 可微的目標函數,我們希望最小化這個目標函數關于參數 θ的期望值,即最小化E[f(θ)].我們使用f1(θ),f2(θ),···,fT(θ)來表示時間步長1,2,···,T對應的隨機目標函數.這個隨機性來自于每個小批量的隨機采樣(minibatch)或者函數固有的噪聲.梯度為gt=?θft(θ),即在時間步長t時,目標函數ft關于參數θ的偏導向量.使用?gt=gt?gt?1表示時間步長t和時間步長t?1對應的梯度差,即本文提到的差分.不同于SGDM 算法只對gt做指數滑動平均,RSGDM 算法對gt和?gt都做指數滑動平均,并用后者的滑動平均值修正前者,下面列出SGDM算法和RSGDM 算法的更新公式.

1)SGDM 算法:

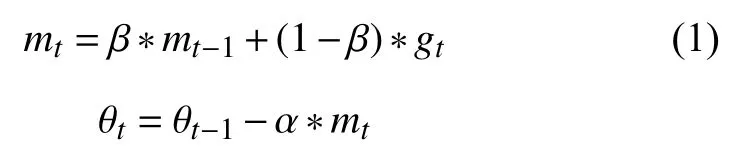
2)RSGDM 算法:

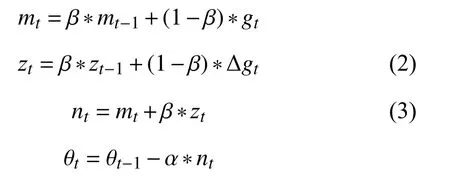
可以看出,RSGDM 算法比SGDM 算法多出式(2)和式(3),本文第2 節將證明SGDM中的式(1)mt對總體gt的估計是有偏的,我們就是使用式(2)和式(3)來進行偏差修正的.RSGDM 算法相比于SGDM 算法沒有增加多余的超參,不會增加我們訓練模型調參的負擔.

2 偏差及滯后性分析

首先我們分析用指數滑動平均估計總體梯度的偏差,首先由SGDM 算法中的式(1)可以得到:

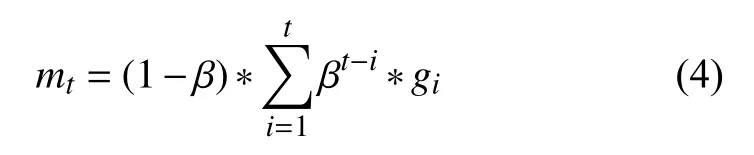
對式(4)兩邊取期望可得:

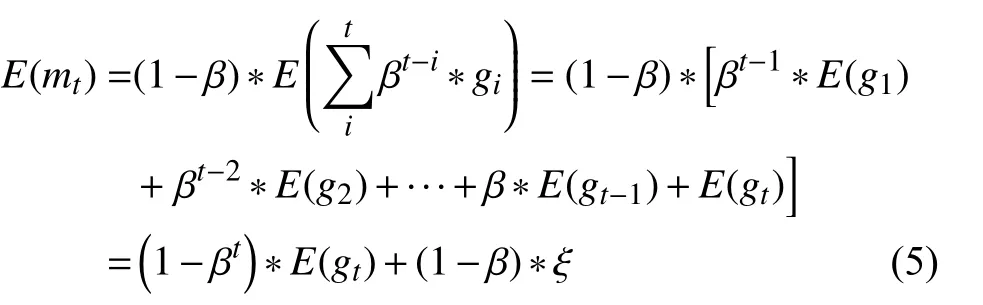
可以發現E(mt)≠E(gt),其中:

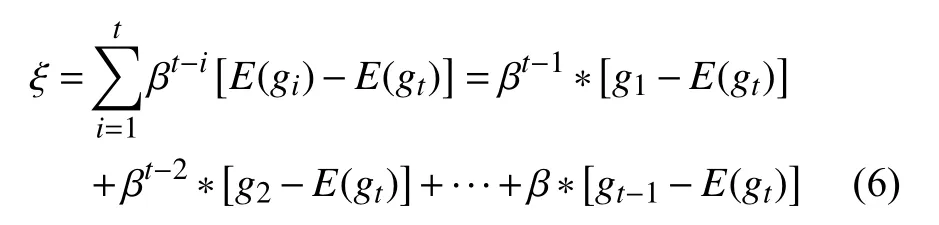
當迭代次數較多時,1 ?βt可以忽略不計,最大的偏差就來自于式(6).如果gt是一個平穩序列,即E(gt)=C(C是常數)時,有ξ=0,此時mt是gt的一個無偏估計.但實際情況下,顯然這是不可能的,所以mt是gt的有偏估計,且偏差主要來自于ξ.并且這個偏差會導致滯后性,比如梯度如果一直處在增大的狀態,由于前面歷史時刻梯度值較小也會導致估計值mt偏小一些,或者梯度如果一直增大,但從某個時刻開始減小,由于歷史梯度的影響梯度的估計值mt可能還沒有反應過來,這就是本文所說的滯后性帶來的影響.針對這種情況我們提出了RSGDM 算法,使用梯度的差分(變化量)估計來修正梯度的估計值mt.直觀上可以這樣理解,如果梯度越來越大且差分的估計也是大于0的,那么這個修正項起到加速收斂的作用,如果梯度越來越大,在某一時刻要開始減小,那這個修正項就會起到修正梯度下降方向的作用.下面我們從公式上解釋RSGDM 算法的優勢:

首先由式(2),我們可以得到:

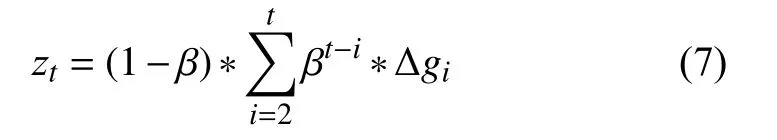
對RSGDM 算法中的式(3)兩邊取期望,我們可以得到:

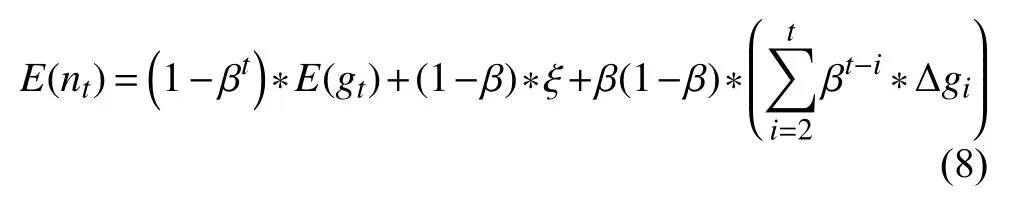
nt是修正后的對gt的估計,我們可以對比式(5)和式(8),我們設不難發現 ?是RSGDM 算法的主要偏差來源,我們展開 ?,得到:

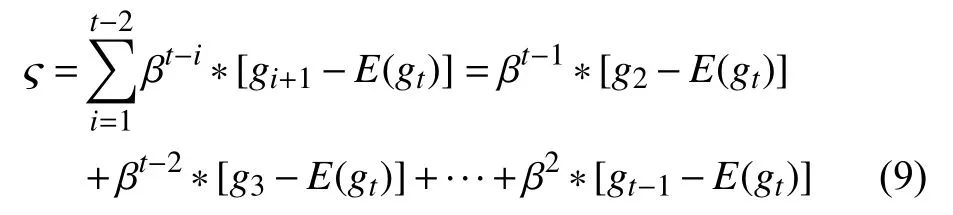
我們對比式(6)SGDM 算法的偏差項 ξ和式(9)RSGDM 算法的偏差項 ?,可以看出ξ受歷史梯度g1,g2,···,gt?1影響,而?受歷史梯度g2,g3,···,gt?1影響.由于t很大且 β 小于0,βt?1?[g1?E(gt)] 接近于0 可以忽略,那么可以得到?=β?ξ.可以看出RSGDM 算法偏差項?少了歷史梯度g1的影響,且由于 β 小于0,所以| ?|≤|ξ|.綜上,我們可以得出RSGDM 算法對比SGDM 算法有更小的偏差,且受歷史梯度影響要小(緩解了滯后性).

3 實驗

本節我們通過實驗證明我們的RSGDM 算法比SGDM 算法更有優勢.我們選擇圖像分類任務來驗證算法的優越性,實驗使用了CIFAR-10和CIFAR-100數據集[12].CIFAR-10 數據集和CIFAR-100 數據集均由32×32 分辨率的RGB 圖像組成,其中訓練集均是50000 張圖片,測試集10000 張圖片.我們在CIFAR-10 數據集上進行10 種類別的分類,在CIFAR-100 數據集上進行100 種類別的分類.我們分別使用ResNet18模型和ResNet50[13]模型在CIFAR-10和CIFAR-100數據集上進行圖像分類任務,每個任務使用SGDM 算法和我們的RSGDM 算法進行比較,評價的指標為分類的準確率.我們使用的深度學習框架是PyTorch,訓練的硬件環境為單卡NVIDIA RTX 2080Ti GPU.實驗中的批量大小(batch-size)設置為128,SGDM 算法和RSGDM 算法的兩個超參數設置一樣,其中動量 β=0.9,初始學習率 α=0.01,訓練時我們使用了權重衰減的方法來防止過擬合,衰減參數設置為5e–4,學習率每50輪(epoch)減少一半.

表1和表2分別給出了ResNet18和ResNet50 使用不同的優化器在CIFAR-10和CIFAR-100 數據集上圖像分類的準確率.我們可以看到在CIFAR-10 數據集上,SGDM和RSGDM 訓練精度都達到了100%,測試精度我們的RSGDM 比SGDM 高了0.14%.在CIFAR-100 數據集上,SGDM和RSGDM 訓練精度都是99.98%,在測試精度上RSGDM 比SGDM 高了0.57%.

表1 ResNet18 在CIFAR-10 上分類準確率(%)

表2 ResNet50 在CIFAR-100 上分類準確率(%)

圖1–圖4給出了ResNet18 在CIFAR-10 上使用SGDM 算法和RSGDM 算法的實驗結果,包括訓練準確率、訓練損失、測試準確率、測試損失.由于我們實驗設置每50個epoch 學習率減半,很明顯可以看出4 張圖在epoch50、100、150 均有一些波動.總體上看在訓練準確率和訓練損失上,兩種方法無論收斂速度和收斂精度都大體相同,在收斂精度上訓練后期我們的RSGDM 算法更具優勢.

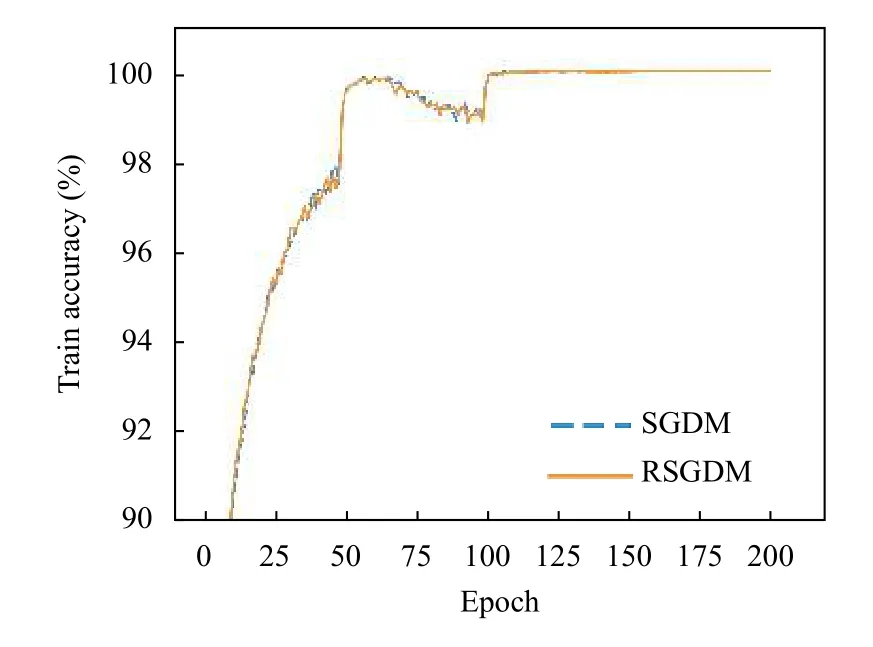
圖1 ResNet18 在CIFAR-10 上的訓練準確率

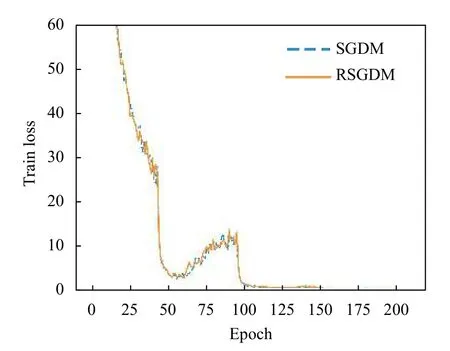
圖2 ResNet18 在CIFAR-10 上的訓練損失

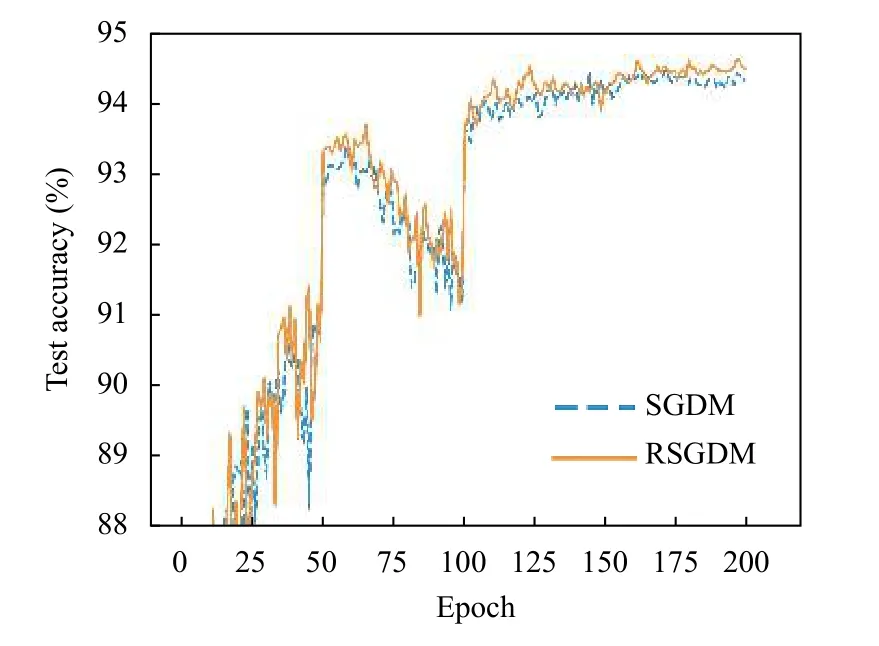
圖3 ResNet18 在CIFAR-10 上的測試準確率

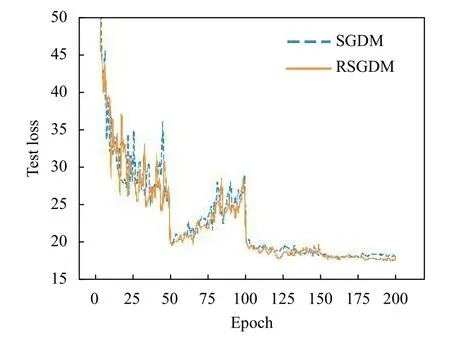
圖4 ResNet18 在CIFAR-10 上的測試損失

圖5–圖8給出了ResNet50 在CIFAR-100 上使用RSGDM 算法和SGDM 算法的實驗結果.可以得出與CIFAR-10 類似的結果,在訓練準確率和訓練損失上二者的幾乎相同,但是在收斂精度上,RSGDM 算法的表現在這個數據集上要領先SGDM 算法很多,可以看測試準確率那張圖,從100個epoch 之后,我們的RSGDM 方法始終準確率高于SGDM,并且最終準確率比SGDM 高了0.57%.這進一步說明我們的方法是有效的.

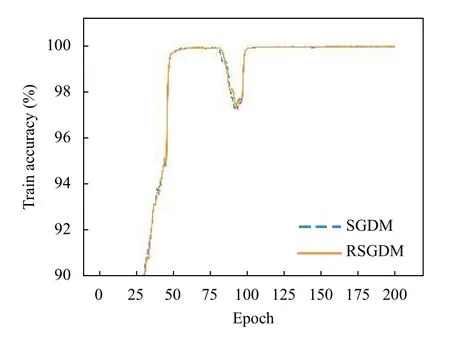
圖5 ResNet50 在CIFAR-100 上的訓練準確率

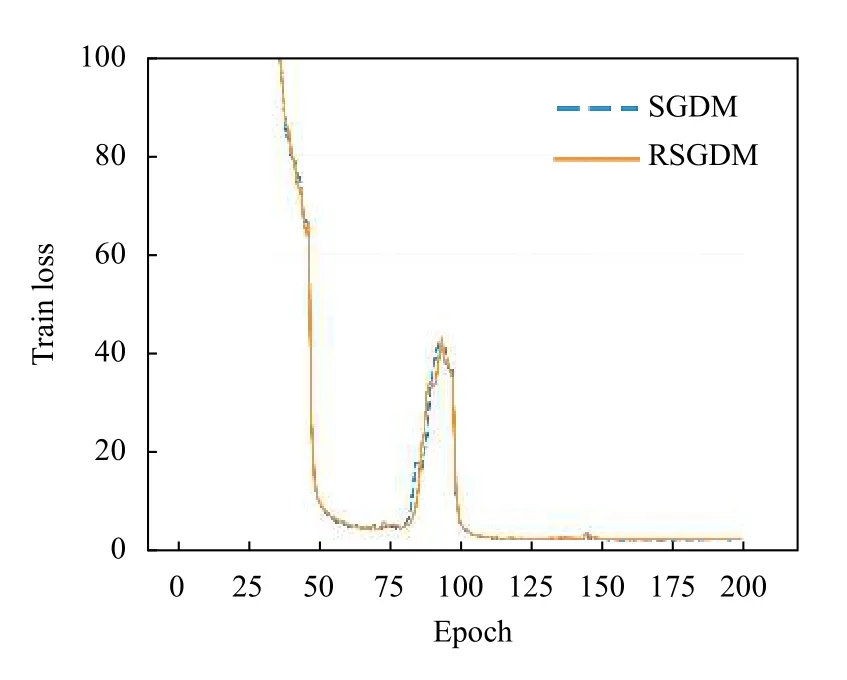
圖6 ResNet50 在CIFAR-100 上的訓練損失

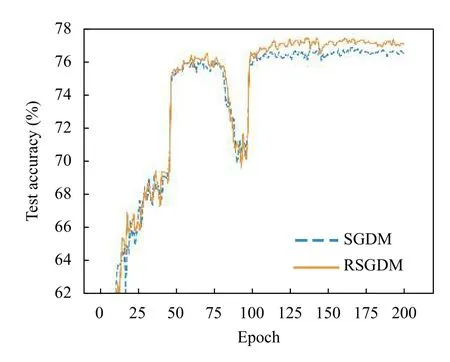
圖7 ResNet50 在CIFAR-100 上的測試準確率

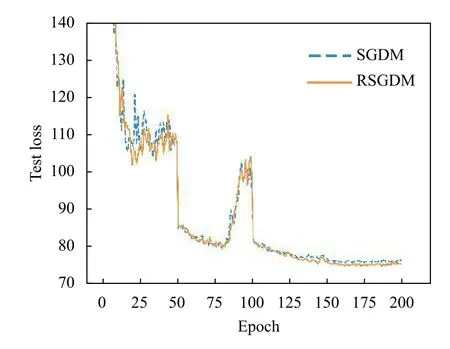
圖8 ResNet50 在CIFAR-100 上的測試損失

4 結論

隨著深度學習模型的不斷復雜化,訓練一個精度高的模型越來越不容易,一個好的優化器具有非常重要的作用.本文分析了傳統方法SGDM 算法使用指數滑動平均估計總體梯度帶來的偏差與滯后性,并理論上證明了這個偏差與滯后性存在.我們提出了基于差分修正的RSGDM 算法,該算法對梯度的差分進行估計并使用這個估計項修正指數滑動平均對梯度的估計,我們從理論上說明了算法的可行性,并且在CIFAR-10和CIFAR-100 兩個數據集上進行圖像分類任務的實驗,實驗結果也進一步說明了我們的RSGDM 算法的優勢.值得一提的是,我們的RSGDM 算法沒有引入更多的需要調試的參數,在不加重深度學習研究員調試超參負擔的情況下,提升了收斂精度.本文開頭介紹了當前這個領域的其他方法,包括現在最常用的學習率自適應性算法Adam 等,未來我們會使用現在的改進思路去提出新的學習率自適應性算法,提出更加準確高效的算法.