融合樸素貝葉斯與決策樹的用戶評論分類算法

賈曉帆，何利力

（浙江理工大學 信息學院，浙江杭州 310018）

0 引言

隨著互聯網的飛速發展，為了滿足用戶需求，出現了網頁、軟件、手機應用等互聯網產品，還包括建立在各類平臺上而開發出的產品，如微信小程序、公眾號等。用戶在互聯網中發表對產品的評價這一舉動讓用戶從單一的信息接受者轉變為互聯網中文本信息的發布者，文本信息量呈指數級增長，僅僅由人工進行分析提取幾乎不大可能，如何有效管理并充分利用這些信息值得思考。

樸素貝葉斯是機器學習的一個常用分類模型，模型本身是建立在貝葉斯定理和特征條件獨立假設上的，有著堅實的數學基礎，用概率統計知識對樣本數據集進行分類。1990 年，Kononenko 等［1］證明了樸素貝葉斯的有效性。樸素貝葉斯的優勢在于能夠很快地在訓練集中建立起貝葉斯模型，但是在有些實際應用中分類效果卻不盡如人意。因為在用貝葉斯分類的前提下，必須假設屬性獨立，即屬性之間沒有關系，當該假設不成立時，就會影響貝葉斯分類效果。為了解決該問題，學者們放松屬性之間相互獨立的條件假設，提出了貝葉斯網絡分類器［2］，其基本思想是考慮全部或者部分屬性之間的關聯性，以此滿足樸素貝葉斯模型相互獨立的條件假設。盡管這種思想能提高分類性能，但是在訓練中需要測算所有屬性之間的相關性，導致算法復雜度劇增。1996 年，Sahami［3］提出K-依賴貝葉斯分類器，有效提升了分類性能；1997 年，Friedman 等［4］提出了一種樹擴展的樸素貝葉斯分類器，簡稱TAN 模型，它在測算屬性之間相關性的基礎上，構建樹形結構圖；1999 年，Nurnberger 等［5］提出了基于神經模糊的樸素貝葉斯分類器，簡稱BAN 模型，它是TAN 模型的升級版，相比TAN 模型，允許特征屬性之間形成有向結構圖；2004 年，Wang 等［6］提出基于自適應的Boosting 與樸素貝葉斯結合方法，可以有效地緩解噪聲提高分類性能；2008 年，徐光美等［7］通過基于互信息計算各屬性與各類別之間的相關性，選擇不相關的特征值代入樸素貝葉斯模型中；2011 年，Zheng 等［8］通過刪除一部分相關性強的特征屬性，將處理后的特征屬性應用于樸素貝葉斯分類模型；2014 年，杜選［9］提出一種基于加權補集的樸素貝葉斯文本分類模型，這種模型可避免在訓練集不平衡時，可能導致分類性能低的缺陷。

本文在研究樸素貝葉斯算法的基礎上提出一種與決策樹相融合的算法，使用本文算法可以有效填補數據集中的缺失屬性值。實驗結果證明，本文算法的分類效果比傳統樸素貝葉斯分類效果更好。

1 理論基礎

1.1 Laplace 方法

Laplace 是最古老的平滑技術之一，所謂平滑技術是指為了產生更理想的概率以調整最大似然估計的技術［10-11］。計算公式如下：

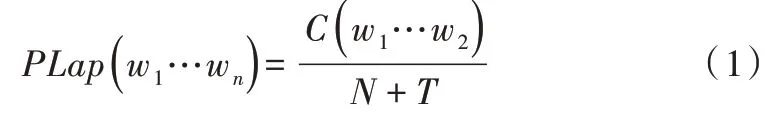
其中，N 為訓練實例總數量；T 為訓練集實例種類數。在Laplace 估計中，先驗概率P（Y）被定義如下：

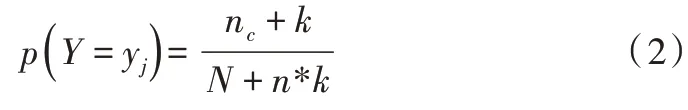
其中,nc是滿足Y={yj} 的實例個數，N 是訓練集個數，n是類的個數，并且k=1。

1.2 樸素貝葉斯

樸素貝葉斯分類（NBC）是一種假設特征與特征之間相互獨立的算法，它基于貝葉斯定理，算法邏輯穩定且簡單，樸素貝葉斯的健壯性較好，其分類功能在數據展現出不同特點時，差別不大，也即在不同類型的數據集中不會表現出太大差異［12］。因此，當數據集屬性之間的關系相對獨立時，樸素貝葉斯分類算法會有較好的效用。

（1）貝葉斯定理。根據條件概率可知，事件A 在事件B已發生的條件下發生概率為：

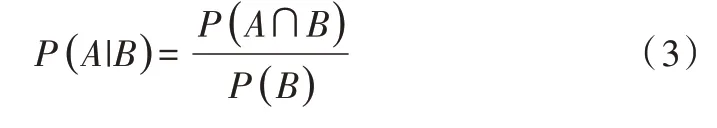
同樣地，在事件A 已發生條件下事件B 發生的概率為：

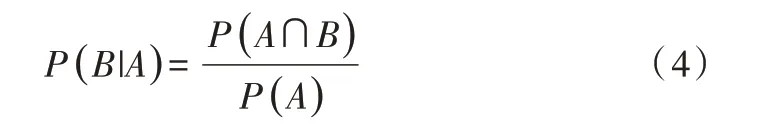
結合兩個方程式可以得到：

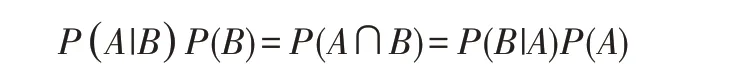
上式兩邊同除以P（A），若P（A）為非零，可以得到貝葉斯定理：

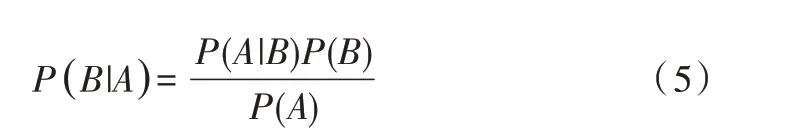
（2）樸素貝葉斯定理。設有樣本數據集D={d1,d2,…,dn}，對應樣本數據的特征屬性集為X={x1,x2,…,xd}，有類別集合Y={y1,y2,…,ym}，即D可以分為ym類別。其中x1,x2,…,xd相互獨立且隨機，則Y的先驗概率P=P(Y)，Y的后驗概率P=P(Y|X)，由樸素貝葉斯算法可得后驗概率為：

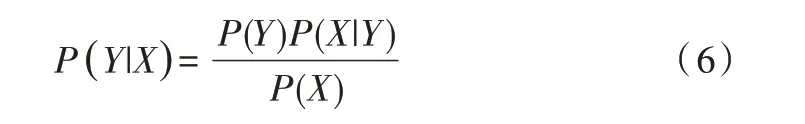
樸素貝葉斯基于各特征之間相互獨立，在給定類別為y的情況下，式（6）可以進一步表示為：

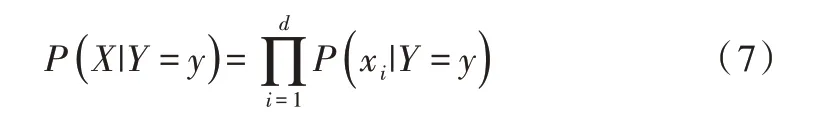
由式（7）可計算出后驗概率為：

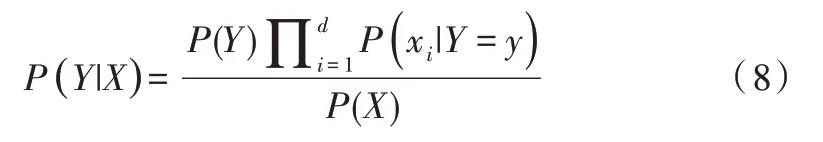
由于P(X)的大小固定不變，因此在比較后驗概率時，只比較式（8）的分子部分即可。因此，可以得到一個樣本數據屬于類別yi的樸素貝葉斯計算公式如下：

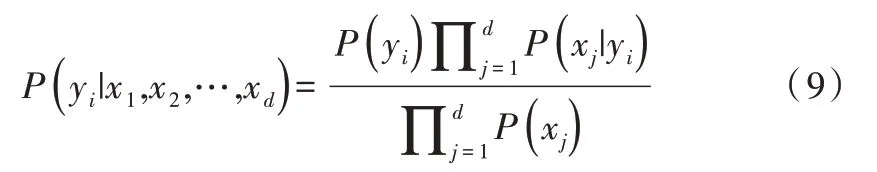
1.3 決策樹

決策樹是一種包含根節點、內部節點、葉節點3 種節點的樹型結構。當文本分類算法為決策樹時，它由樹的內部節點逐一標注所構成，葉節點表示對應的類別標簽，與葉節點相連的分支上標注著其對應的權重，樹的葉子節點表示文本分類目標，當從根開始遍歷查詢最終到達某一個葉子節點，這樣就完成了一次文本分類［13］，樹的高度就是時間復雜度，它是一個自頂向下、分而治之的總過程。決策樹的準確率會因重復的屬性而受一定影響，因而用決策樹進行分類是要對數據進行特征選擇。決策樹在開始階段會浪費時間，但只要模型建立起來，運用階段非常快。

決策樹算法是一種無監督分類方法，決策樹的生成主要分為節點分裂和閾值確定，節點分裂指當一個節點所代表的屬性無法判斷時，則選擇將一節點分為多個子節點，而選擇適當的閾值可以使分類錯誤率最小。決策樹以樹的層次規則為特征，葉子節點為分類目標，通過遍歷根節點到葉子節點完成一次分類操作。決策樹分類算法與其他決策支持工具相比較起來易于理解和解釋。然而，通過有限的數據集無法訓練出可靠的類標簽，并且對特征空間計算成本非常高，這對決策樹而言是一種限制［13］。決策樹算法作為一種常見分類算法，有很多變種，包括ID3、C4.5、C5.0、CART 等。其中，最常用的、最經典的是C4.5 算法。

2 改進思想

2.1 樸素貝葉斯概率優化

樸素貝葉斯的概率估計會在訓練樣本不足時出現零概率的問題，這會導致求出的類標簽的后驗概率值為零，使用連乘計算文本出現概率時也是零，傳統的樸素貝葉斯在這種情況下無法進行分類，這一直以來都是樸素貝葉斯的難題。為了解決該問題，法國的數學家拉普拉斯（Lapla?cian）首次提出一種加法平滑方法，對每個詞的計數加1，該加法平滑也叫拉普拉斯平滑。該方法基于一定的數學理論基礎，在數據集較大的情況下，每一個詞出現的次數加1之后對概率估計結果的影響可完全忽略不計，但是卻可以有效地避免出現零概率問題。針對本實驗所采取的樸素貝葉斯模型，采用詞頻估算每一個特征，其經過拉普拉斯平滑方法處理后的表達式為：

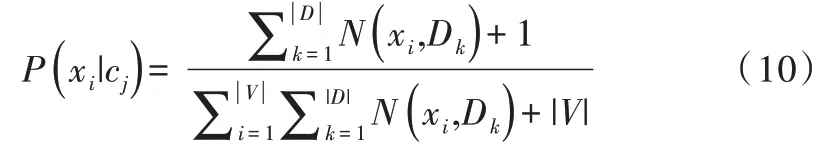
2.2 樸素貝葉斯與決策樹融合

為了提高貝葉斯分類準確性，在提出的貝葉斯與其他方法相結合的算法中，最為代表的是Kohavi［14］提出的NB?Tree 算法。對于大型數據分類，決策樹和樸素貝葉斯相比，前者在維度較大或者屬性之間的依賴關系明顯優于后者，后者的分類結果準確性優于前者。而NBTree 算法剛好結合貝葉斯和決策樹各自的優點，提升了算法效率。

C4.5 算法的優點是產生的分類規則易于理解，準確率較高，C4.5 經過樹生成和樹剪枝建立決策樹。在計算每個屬性的信息增益率（Information GainRatio）后，選出信息增益率最高的屬性對給定集合測試屬性，再采用遞歸算法根據測試屬性建立分支，初步得到決策樹。

在用決策樹對測試樣本數據進行分類時可能會有某些屬性值缺失，傳統的決策樹算法在面對這些缺失的屬性值一般會采用拋棄缺失屬性值或者重新給定一個在訓練樣本中該屬性常見的值［15］。而C4.5 算法會采用概率分布填充法處理缺失屬性值，具體執行過程：首先為某個未知屬性每個可能的值賦予一個概率，再計算某節點上屬性不同值的出現頻率，這些概率可以被再次估計［16］。C4.5 算法相關計算公式如下所示［17］。

（1）期望信息（也稱信息熵）。設S是Si個數據樣本的集合，假定類標號屬性有m個不同值，定義m個不同類Ti(i=1,…,m)。設Si是類Ti中的樣本數。對一個給定的樣本分類所需的期望值為：

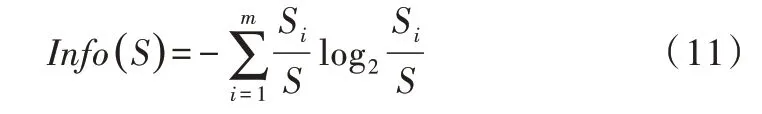
（2）信息增益。由屬性A劃分成子集的信息量為：

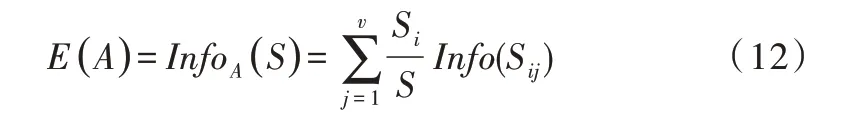
信息增益為原來的信息需求與新的需求之間的差。即：

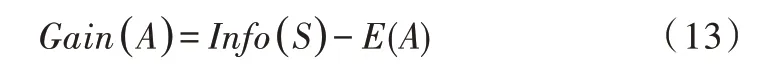
（3）信息增益率。C4.5 算法中引入了信息增益率，屬性A 的信息增益率計算公式為：

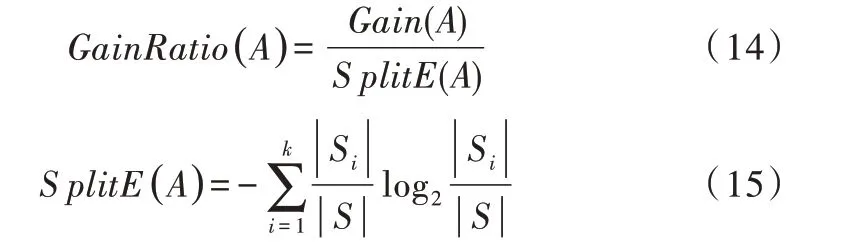
在決策樹的剪枝階段，C4.5 算法采用后剪枝技術形成決策樹模型，根據建立好的模型生成一系列IF-THEN 規則，實現對訓練集的分類。

C4.5 算法雖然在處理噪聲方面有很強的能力，但是在訓練集缺失屬性值很高的狀態下，使用C4.5 算法構建的決策樹模型會變復雜并出現更多的結點數，最終分類準確率也會下降［18］。鑒于樸素貝葉斯分類具有堅實的理論基礎、較小的出錯率，本文提出一種基于樸素貝葉斯定理的方法［19］，以處理空缺屬性值。

假定一個樣本訓練集D={d1,d2,…,dn}，每一個訓練實例描述為di={di1,di2,…,dih}，對應樣本訓練的特征屬性集A={A1,A2,…,An}，每個屬性Ai的屬性值是{Ai1,Ai2,…,Aih} 。訓練集包含的類別集合C={C1,C2,…,Cm}，即D可以分為Cm類別。與訓練集D 有關系的決策樹有如下特點：①內部節點由Ai表示；②子節點屬性與父節點屬性用枝干相連；③葉節點由Ci表示。樹被建立起來后對每個測試實例進行分類，實例di的結果就是一個類別。基本步驟為：一是用訓練集構造一個決策樹；二是將概率優化后的樸素貝葉斯運用到測試集D 中。

對于訓練集D，首先運用決策樹分類器對每個di進行分類。如果訓練集中沒有空缺屬性，則將數據壓入D1 集合，如果有，則按空缺個數壓入D2 集合，數量越少越排前，到所有數據都檢測完則結束，最后形成了D1 和D2 兩個集合，其中D1 放入的是沒有空缺屬性值的數據集合，D2 放入的是包含空缺屬性值的數據集合；讀取D2 中的數據，用概率優化后的樸素貝葉斯處理空缺屬性后放入D1 中，遞歸直到D2 集合中數據為0。處理完訓練集D 中的空缺屬性值后，再用決策樹對更新后的訓練集進行分類。

3 實驗分析

3.1 實驗數據

本文實驗選取的是某互聯網營銷平臺微信公眾號中活動的91 120 條中文用戶評論，通過考察用戶評論，將數據分為積極和消極兩類數據，并選用準確率和召回率評價分類效果。部分數據如表1 所示。

Table 1 Data of some user comments表1 部分用戶評論數據

3.2 數據預處理與文本特征抽取

數據預處理包括3 個部分，即：文本正則化、切分成詞和去掉停用詞。運用TF-IDF 方法抽取數據特征，如表2 所示。

Table 2 Data preprocessing and text feature extraction表2 數據預處理與文本特征抽取

3.3 樸素貝葉斯與決策樹分類融合

采用融合樸素貝葉斯和決策樹的算法對用戶評論進行分類，最終正確地將用戶評論分為積極和消極兩類，如表3 所示。

Table 3 Classification results表3 分類結果

本文實驗結果采用準確率和召回率兩個指標，計算公式如下：

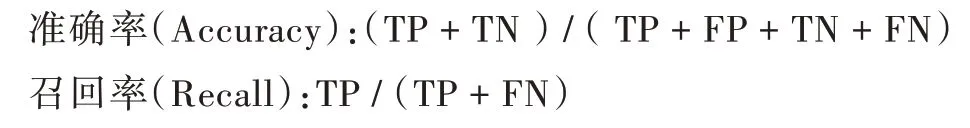
其中，TP 表示正確的標記為正，FP 錯誤的標記為正，FN 錯誤的標記為負，TN 正確的標記為負［20］，如表4 所示。

Table 4 Parameter meaning表4 參數含義

最終計算得到的分類準確率和召回率如表5 所示。

Table 5 Analysis of experimental results表5 實驗結果分析

由表5 可知，為了對比本文中提出的算法是否可行有效，通過對比樸素貝葉斯對用戶評論的分類，本文算法準確率高出0.5 個百分點，召回率高出0.2 個百分點。由此可見，在用戶評論文本分類中，融合樸素貝葉斯和決策樹用戶評論分類效果取得了不錯的結果。

4 結語

為了實現對用戶評論的商業研究價值提取，解決互聯網產品后續優化和增進服務問題，本文提出了一種融合樸素貝葉斯與決策樹的用戶評論分類算法。該研究首先對文本正則化、切分成詞并去掉停用詞，再融合樸素貝葉斯和決策樹算法，并將其應用于微信公眾號互聯網營銷用戶評論分類中，最終可以正確地將用戶評論分為積極和消極兩類。其中，積極的用戶評論可以作為后續互聯網營銷活動優化，提升用戶體驗的重要參考依據，消極的用戶評論可以增進自己的服務。對分類結果的分析表明，改進后的算法解決了樸素貝葉斯的零概率問題和決策樹因屬性值缺失率高導致的分類準確度下降問題，提高了分類準確率。由于數據集不足以及中文語義復雜，會造成評論分類出現相反的情況，后續要在語義情感特征準確性提取上作進一步研究。