以網絡拓撲距離為特征的有效藥物組合預測

任 彪

（上海理工大學 管理學院，上海 200093）

0 引言

將兩種或以上藥物組合在一起治療某種疾病，能夠產生協同作用，治療效果遠大于單個藥物作用的效果，即為所謂的組合用藥［1］。組合用藥作用于多個靶點，避免了可能引起的反饋機制，減少了藥物毒副作用［2］。基于這些優勢，可明確組合藥物對于復雜疾病，如癌癥、心血管疾病等具有更好的治療效果，因此組合用藥具有重要的研究價值［3］。傳統藥物組合的發現是基于高通量實驗篩選，通過分析高維實驗數據，判斷藥物之間是否會產生協同作用，進而確定藥物組合［4］。但如今藥物總體數量龐大，藥物配對的數量超出了高通量實驗能夠承受的范圍。組學技術的出現可幫助研究者解決這一難題，其結合目前積累的大量數據和經驗，有效利用生物信息學和計算工具，挖掘出可靠的信息及各生物信息之間的潛在關系［5］。通過該方法既能發現藥物的作用機制，又能降低研究成本、縮短研究周期。

近年來，各種針對藥物組合的預測方法發展迅速，其中一些利用組合特征之間的相似性建立機器學習模型以預測有效的藥物組合。如Xu 等［6］整合生物學（靶蛋白、疾病通路）、化學（二維結構、化合物相互作用的可能性）及藥理學信息（藥物療效），運用隨機梯度提升算法預測藥物組合。此外，對于非線性的動態作用數據，基于數學模型的方法具有不錯的效果。如針對特定分子的常微分方程（ODE）模型，以及針對分子運作過程的Petri 網絡模型等［7-9］。但這些方法都有不足之處，例如基于數學模型的方法需要豐富的動力學參數，否則會降低預測效果［1］。

除上述方法外，基于網絡的方法也得到了廣泛應用，利用網絡探索目標在網絡上的關聯情況，預測潛在的協同藥物組合。如Zou 等［10］描述藥物靶點與其鄰居在PPI 網絡中的相互作用，區分協同藥物組合；Chen 等［11］構建一個通路—通路的相互作用（WWI）網絡，描述復雜的通路—通路之間的關系，從基于通路的角度探討藥物協同作用［12］。這些方法考慮兩個藥物的靶點在網絡中的拓撲關系，但并沒有考慮其與疾病單元之間的關系。故本文引入藥物—藥物—疾病單元三者在蛋白質相互作用網絡中的拓撲距離作為特征，結合生物學和藥理學相似性特征，利用支持向量機、邏輯回歸和隨機森林3 種機器學習算法構建藥物組合預測模型。若藥物能夠作用于更多疾病單元中的基因，即兩個藥物需要同時作用于疾病單元，且兩者作用于疾病單元的部分盡可能不重合［13］，則能獲得更好的治療效果。將這三者在蛋白質相互作用網絡中的拓撲關系轉化為兩兩之間的距離，以此作為特征進行預測，最終提高預測效果。

1 特征工程

1.1 數據準備

本文采用的樣本數據主要來源于Drug Combination Database（DCDB，version 2.0），DCDB 包含1 363 種藥物組合，這里選取用于治療高血壓的86 對藥物組合作為研究對象。Drugbank 數據庫是一個提供生物信息和化學信息的數據庫，其具有詳細的藥物數據和全面的藥物目標信息［14］。從drugbank 數據庫中獲取藥物的靶標信息、二維分子結構信息與ATC 編碼信息，其中靶標的蛋白質序列信息來自UniProt 數據庫（http：//www.uniprot.org/），高血壓的致病基因來自OMIM 數據庫［15］，包括目前所有已知的遺傳病以及超過15 000 個基因信息。蛋白質相互作用信息源自Menche 等［16］提供的蛋白質互作文件和HuRI-人類蛋白互作組數據庫（http：//www.interactome-atlas.org/），最新公布的HuRI-人類蛋白互作組數據庫中包含了9 094 個獨立蛋白構成的64 006 對相互作用關系［17］。

1.2 正負樣本構建

將每個藥物的化學結構信息、ATC 編碼信息、靶標信息與蛋白質序列信息進行整合，并與86 對藥物進行組合匹配，若藥物組合缺失以上任意一個信息，該組合將被刪除。通過整合刪選，最終留下81 對治療高血壓的藥物組合，以此作為正樣本。這81 對藥物組合包含69 種獨立藥物，將其兩兩組合，共得到2 346 種組合。排除DCDB 中已出現的組合，從剩下的組合中挑選81 對組合作為負樣本。

1.3 蛋白質相互作用網絡構建

將參考文件和HuRI-人類蛋白互作組數據庫中的蛋白質相互作用數據取并集之后，共獲得由15 063 個獨立蛋白質所構成的187 371 對相互作用關系。利用uinprot 在線mapping 工具，將這些蛋白質名稱統一轉化成Entrez_ID，以便于構建蛋白質網絡，并保證靶標及致病基因的ID 相同。將15 063 個蛋白看成15 063 個節點，每一對相互作用視為一條邊，即可構成一張蛋白質相互關系的網絡圖。

1.4 特征構建

1.4.1 化學結構相似性

若兩個藥物化學結構的相似性分數越高，則其更有可能產生相似作用，這里調用第三方包RDkit 計算兩個藥物化學結構的相似性。首先利用獲得的每個藥物分子的二維結構信息（smiles）調用RDkit 計算對應的二維MACCS 分子指紋［18］，其是一種基于SMARTS、長度為167 的分子指紋，然后利用Tanimoto 系數計算二維MACCS 分子指紋的相似度。兩個藥物的Tanimoto 相似度定義如下：

式中，a 代表藥物A 分子指紋中的分子位數，b 代表藥物B 分子指紋中的分子位數，c 代表A 和B 中相同的位數。

1.4.2 藥物療效相似性

藥物療效相似性是指藥物在治療疾病時功能相似，其在預測協同藥物組合中具有重要作用。ATC 編碼是解剖治療學及化學分類系統編碼，可表示藥物療效信息。編碼由7 位組成，共分為5 級：第1 級為一位字母，第2 級為兩位數字，第3 級為一位字母，第4 級為一位字母，第5 級為兩位數字，分別表示藥物在解剖學、治療學、藥理學、化學、化合物上的分類。對于有多個ATC 編碼的藥物，需要計算每一對ATC 編碼的相似性Sk(A,B)，最后選擇最大的Sk(A,B)值作為藥物療效相似性的數值。藥物療效相似性定義如下：

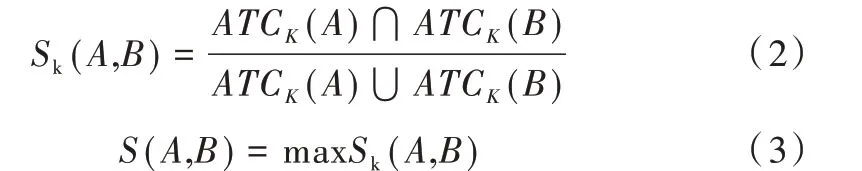
式中，ATCK代表藥物ATC 編碼。

1.4.3 靶標序列相似性

利用萊溫斯坦距離［19］計算兩個藥物靶標序列的相似性，其可用來計算兩個不等長序列的相似性，原理是計算出將序列A 變換成序列B 需要變換的次數。

式中，a、b 為兩個數組（字符串），i、j為數組下標，這里可直接調用Python 中的固定模塊進行計算。

1.4.4 靶標單元與疾病單元距離計算

首先需要將藥物靶標信息和高血壓致病基因信息轉化成Entrez_ID，并將其映射到相互作用網絡中，刪除蛋白質網絡中的獨立節點和不在網絡中的靶標。藥物靶標或致病基因在網絡中往往位于相鄰位置，所以認為藥物—藥物—疾病單元三者之間的位置關系滿足互補性的拓撲關系時，對于預測協同藥物具有很大幫助［20］。利用d（X，Y）表示藥物X 與疾病單元Y 之間距離，具體公式如下：

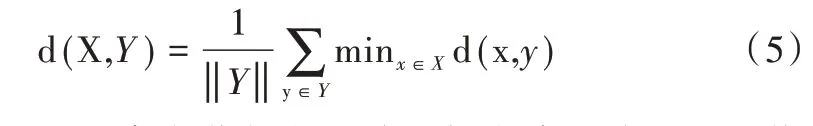
式中，d（X，Y）代表藥物靶蛋白x 與疾病蛋白y 在網絡中的最短距離，可采用Python 計算得到。

1.4.5 兩個靶標單元之間距離計算

計算兩靶標之間距離與計算靶標單元到疾病單元的距離相似。由于兩個藥物靶標單元中含有的蛋白數量為同一數量級，故可通過比較靶標單元之間最短距離和兩個靶標單元在網絡中半徑的均值來計算靶標單元之間距離。具體公式如下：

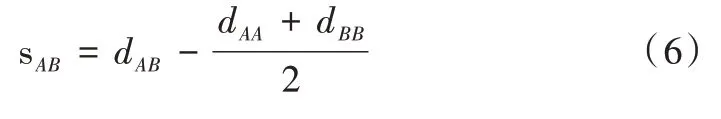
2 機器學習模型

監督學習分為學習和預測兩個過程，其任務是學習一個模型，使模型對于任意給定的輸入會預測最好的結果作為輸出［21］。模型是通過對訓練數據集的學習獲得的，之后再對測試樣本集進行預測。監督學習利用的數據集都由特征及其對應標簽組成，將測試集的特征向量作為模型輸入，并將得到的結果與特征向量原有標簽進行對比，從而獲得模型預測的準確度。例如，每對藥物組合具有5 個特征，其對應1 個標簽，即如果該組合有效則為1，否則為0。機器學習算法會對訓練集中的特征和標簽進行學習，分析一組特征是有效還是無效，并形成自己的判別標準，從而判斷測試的數據是否有效。

2.1 支持向量機

支持向量機（Support Vector Machines，SVM）于1964 年被提出后得到了迅速發展，并在多個領域獲得青睞，目前已應用于人像識別、文本分類等多個模式識別問題中［22］。其是監督學習中的二分類模型，目的是找到一個超平面分割正負樣本，并遵循間隔最大化原則。這也是其與感知機的區別所在，最終轉化為一個求解凸二次規劃問題。超平面，通俗的講就像二維平面中的直線或三維空間中的一個平面，以此類推。在對超平面沒有限制時，現實中可以找到無數個這樣分割正負樣本的直線或平面，但當限定間隔最大時，則只能找到唯一滿足條件的超平面。通過線性函數能對樣本分類，則稱這些數據樣本線性可分，可利用支持向量線性分類器對其進行分類。然而，對于那些非線性樣本，可通過核函數和軟間隔最大化形成非線性支持向量機，本質上還是將非線性問題轉化成線性問題進行處理。本文綜合考慮后采用了線性支持向量機。

2.2 邏輯斯蒂回歸

邏輯斯蒂回歸（Logistic Regression）屬于統計學習算法中的經典分類方法，其是一種線性模型［23］。邏輯斯蒂回歸在線性回歸模型基礎上，使用Sigmod 函數估計預測結果概率P（y | x）的大小。邏輯斯蒂回歸并沒有對數據分布進行建模，其不知道數據具體分布，而是直接求解分類超平面。在本文的應用中利用邏輯斯蒂回歸模型直接計算藥物組合是有效組合的概率，范圍在0～1 之間，大于0.5 時則被認為有效。

2.3 隨機森林算法

隨機森林算法（Random Frost）是基于Bagging 集成學習理論的代表算法，由Leo 于2001 年提出［24］。作為一種新興的、高度靈活的機器學習算法，具有廣闊的應用前景，在準確率方面相當具有優勢。隨機森林是指通過集成學習思想將多棵樹集成的一種算法，其基本單元是決策樹，而其本質屬于機器學習中的集成學習（Ensemble Learning）方法。通俗的講，在分類問題中，每棵決策樹都是一個分類器，N 棵樹就會有N 種結果，隨機森林集成了所有投票結果，將投票次數最多的類別視為最終結果。隨機森林能夠有效運行在大數據集上，但當數據量較小時會出現過擬合現象，其還能夠處理具有高維特征的輸入樣本，且不需要降維，并能評估各個特征在分類問題上的重要性。

3 模型構建與結果分析

運用上述3 類模型與計算出的特征進行有效藥物組合預測，選擇一倍于正樣本的負樣本構建模型。根據簡單交叉驗證原理，從數據集中選取75%的樣本作為訓練集，25%的樣本作為測試集。本文利用AUC（ROC 曲下面積）、Ac?curacy、F-measure、Recall、precision 作為模型評價標準，將未加入3 個距離特征與加入距離特征后的模型預測結果進行比較。

3.1 ROC 曲線

ROC（Receiver Operating Characteristic）在機器學習領域用來評判分類、檢測結果好壞，是一種重要與常見的統計分析方法［25］。混淆矩陣是ROC 曲線繪制的基礎，主要涵蓋4 個指標：TP（將正例正確預測為正例）、FN（將正例錯誤預測為負例）、PF（將負例錯誤預測為正例）、TN（將負例正確預測為負例）。在ROC 曲線圖中，每個點以對應的FPR值為橫坐標，TPR 值為縱坐標，其中FPR 為假陽性率，TPR為真陽性率。具體公式如下：

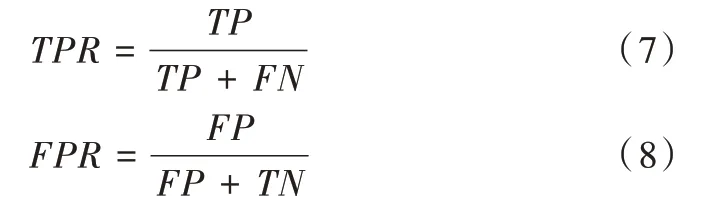
利用4 個指標還可得到精確率（Precision）、召回率（Re?call）和準確度（Accuracy），進一步計算得到F1 評分，其是精確率與召回率的加權平均。具體公式如下：

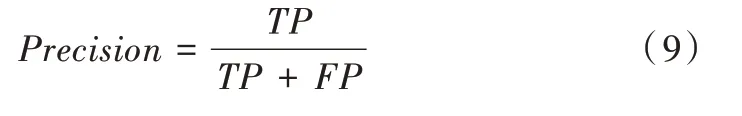
3.2 ROC 曲線下面積

AUC（曲線下面積）可用來評價分類器區分正負類的性能，AUC 的值在0～1 之間，該值越接近1，說明分類效果越好。當AUC 的值等于0.5 時，模型能夠正確分類的概率只有一半，類似于隨機拋硬幣的概率，此時分類效果很差。利用TPR 值和FPR 值，可在對應坐標平面中確定一個點，由各個點確定ROC 曲線。例如，給定一個閾值為0.5，意味著若分類模型對每個實例判斷為正類的概率大于等于0.5，則判斷其為正類，小于0.5 則判斷為負類，在這種情況下計算出TPR 值和FPR 值，則可確定一個點（FPR，TPR）；同樣，將閾值設置為0.6 時，又可確定一個（FPR，TPR）點，這樣眾多點即可構成一條ROC 曲線。理想情況是曲線經過（0，1）點，即FPR 為0，TPR 為1，但在現實中很難達到，所以只要曲線越接近這個點越好。通過計算曲線下方面積，面積越大則曲線越靠近（0，1）點，以此判斷預測結果的好壞。

3.3 預測過程與結果

由于藥物化學結構相似性、藥物療效相似性與藥物靶標序列相似性已在藥物組合預測方面表現突出，故本文首先選擇這3 個特征作為輸入，分別利用當下比較流行的機器學習算法進行預測。利用不同模型進行預測，并對比上述各項評價模型性能指標，最終支持向量機、邏輯斯蒂回歸、隨機森林算法展示出不錯的預測效果。具體指標如表1 所示，ROC 曲線如圖1 所示（彩圖掃OSID 碼可見，下同）。之后為體現藥物—藥物—疾病單元三者在蛋白質相互作用網絡中的距離在預測有效藥物組合中的作用，本文將3個計算出的距離作為特征加入，保持各項參數不變，再進行上述同樣的操作，得到的各項指標如表2 所示，ROC 曲線如圖2 所示。

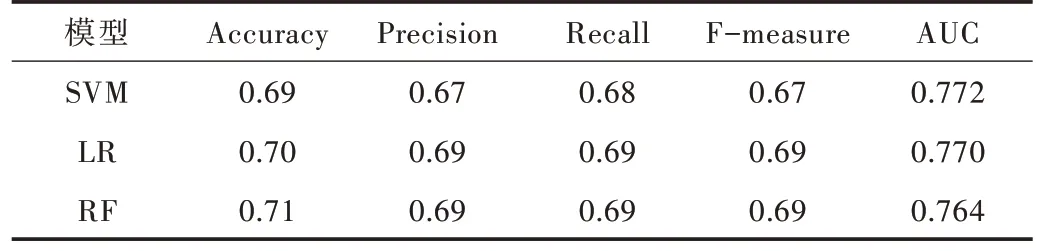
Table 1 Indicators of prediction results of three models（without distance feature）表1 3 個模型（未加入距離特征）預測結果各項指標

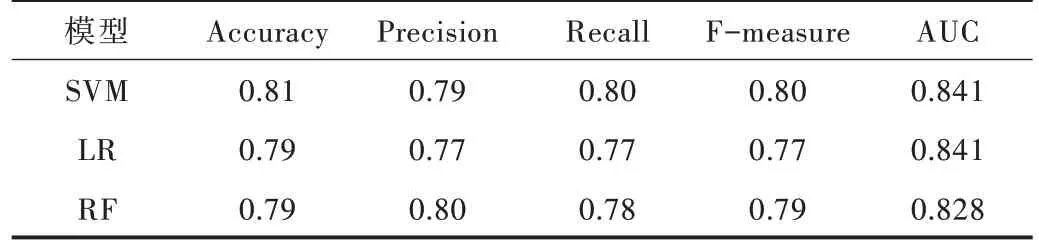
Table 2 Indicators of prediction results of three models（adding distance feature）表2 3 個模型（加入距離特征）預測結果各項指標

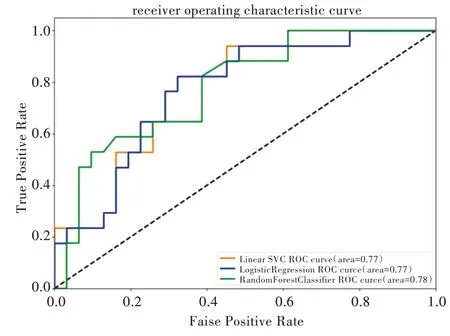
Fig.1 Comparison of ROC curves without distance feature圖1 未加入距離特征的ROC 曲線對比

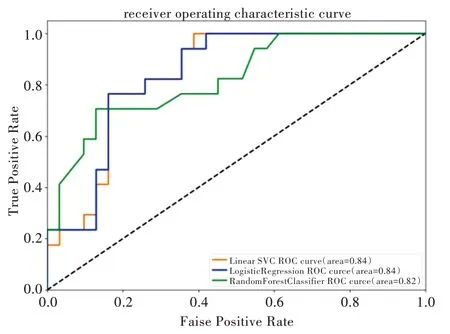
Fig.2 ROC curve comparison after adding distance feature圖2 加入距離特征后的ROC 曲線對比

3.4 結果分析

從表1、表2 對比中可以看出，在未加入距離特征進行預測時，準確率在0.7 左右，且AUC 值相對較低。在加入距離特征后，準確率達到0.8 左右，AUC 值也有所提高。由于樣本數量較少，采用隨機森林算法預測時可能出現過擬合現象，并在實驗中表現為結果不穩定，所以本文以其他兩個模型的準確率作為最終比較依據。支持向量機和邏輯斯蒂回歸的預測結果分別提升了12%與9%。

4 結語

組合藥物的使用無疑可幫助人們治療復雜疾病，同時利用計算機技術、組學和網絡技術幫助人們發現新的藥物組合，因此是一種行之有效的手段。該方法極大地縮小了搜索范圍，在小范圍內再進行實驗檢驗，更為安全、可靠。發現新的可靠特征也是準確預測的關鍵之一，本文引入的網絡距離特征對于提高預測準確率起到了重要作用，加入網絡距離特征后，預測準確率提高了10%以上。本文使用的化學結構特征、藥物療效特征、藥物靶標序列特征基本都是比較經典的，前人都曾經采用過，故可保證其可信度。

此外，網絡距離特征原理上是希望藥物—藥物—疾病單元三者之間能夠滿足一定的特殊條件，即兩種藥物不僅能同時作用于疾病單元，且相互之間可保持足夠的距離。通俗一點講，即希望在作用于更多致病基因的同時，產生的不良反應更小。本文直接運用網絡中三者的距離，并未完全展現出這種互補性關系，所以下一步希望探索出能夠準確描述這種拓撲關系的特征。本文利用的特征相對較少，其他文獻中還運用了化合物相互作用、蛋白質相互作用等特征，故本文之后也會結合生物學、藥理學、化學等多種類的數據特征，融合靜態數據與動態數據進行藥物組合預測。本文所用模型都是監督模型，而負樣本是隨機構建的，不排除當中會有有效的藥物組合，若利用半監督模型或其他更先進的算法，相信在預測精度上會得到進一步提升。