考慮時變間隙的并聯指向機構非線性模態分析

孫 靜 韓雪艷 魏元浩 陳 爽 李仕華

1.燕山大學機械工程學院，秦皇島，0660042.燕山大學河北省并聯機器人與機電系統實驗室，秦皇島，066004

0 引言

并聯指向機構作為一種工作性能要求很高的精密設備，必須具有高精度、高可靠性和長使用壽命等特征。機構的支承或構件在生產加工和裝配中產生的微小誤差以及在各種復雜環境中長期使用后產生的磨損都可能導致機構運動副出現間隙，這些運動副間隙相比結構本身的尺寸可能很小，但是在間隙內產生的零部件接觸-分離的碰撞現象會導致剛度的突變，降低機構的運動精度，使其運動軌跡出現非線性波動，令機構出現明顯的振動現象[1]，同時也會對機構的模態特性產生影響。固有頻率的變化可能會導致不可預測的共振發生，從而大大降低設備的工作精度和使用壽命。然而實際中往往無法直接使用設備樣機進行含間隙機構非線性模態實驗，因此有必要尋找有效的方法建立含間隙并聯指向機構振動模型以對其非線性模態特性進行分析。

模態和間隙振動特性研究是進行含間隙機構動力學優化、壽命預測和故障診斷的基礎，國內外學者已經開展了許多相關研究。李艷清等[2]利用加權平均方法對含間隙兩自由度彈簧-質量分段振動系統的非線性模態進行了研究。張艷龍等[3]將Dankowicz動摩擦模型引進力學系統中，結合數值仿真方法研究了非光滑因素間隙及摩擦作用下強非線性系統動力學行為。李新泉等[4]建立了一類兩自由度含間隙碰撞振動系統動力學模型，并構建了Poincaré映射方程，采用數值計算方法探究了系統的混沌振動特性。唐俊杰等[5]考慮受力變化頻繁的關節處運動副間隙，利用有限元軟件和靜力學計算分析了運動副間隙對機構模態振動特性的影響。尹鳳偉等[6]基于一類帶有間隙-彈性約束的兩自由度受迫振動系統，通過多目標和多參數協同仿真分析，研究了非光滑振動系統的周期性沖擊振動特征。ZHAO等[7]研究了一種基于改進變分模式分解的分解技術以自適應提取一系列頻域特征，并有效地檢測氣門機構間隙異常故障。王強等[8]基于模態綜合法，結合有限元分析和模態試驗對含間隙折疊舵面的非線性動態特性進行了分析。上述文獻針對不同特征結構所進行的非線性振動分析多屬于仿真以及針對間隙或其他非線性因素的研究，對動態間隙和非線性振動特性之間聯系的理論研究并不充分，且研究對象多具有對稱特性或為簡單機械結構，因此有必要針對考慮運動副間隙的復雜空間并聯指向機構模態特性進行深入研究。

本文針對SUN等[9]提出的一種新型3-RRCPR并聯指向機構，將數軸法應用到具有復雜空間結構的并聯指向機構的振動系統建模中，并驗證其可行性；考慮殘余剛度，提出含間隙運動副的改進非線性等效剛度系數建立方法，并建立考慮時變間隙的非線性振動模型。

1 含間隙機構振動系統建模

1.1 基于數軸法的機構振動系統建模

圖1所示的3-RRCPR六自由度并聯指向機構[9]具有3條構造相同的支鏈，每條支鏈由固定于基座上的轉動驅動副、第1連桿、從動轉動副、第2連桿、等效圓柱副和位移驅動副組成，動平臺和3條支鏈的位移驅動電機之間通過轉動副連接。機構通過驅動轉動副調整姿態，通過微動移動驅動副調整動平臺位置。

圖1 3-RRCPR并聯指向機構構型[9]Fig.1 3-RRCPR parallel pointingmechanism configuration[9]

若采用常用的動力學建模方法(如拉格朗日方程等)來對該機構的振動特性進行建模分析，則建模的難度很大，且由于存在大量結構和力傳遞參數，求解過程也會十分困難，甚至會出現數學模型求解失敗的情況,在進行具有針對性的振動模態分析時，若采用此類建模方法，將嚴重影響分析效率且無法保證能夠得到計算結果。

為降低考慮間隙的空間并聯指向機構非線性模態建模與求解的難度，本文將數軸建模法[10]應用到圖1所示機構的振動模型建模中。由于機構的阻尼和振幅都很小，故將結構中慣性和剛度較大的部件視為質量集中的質點，慣性小且結構剛度較小的部件視為無質量彈簧阻尼系統。機構的基座、驅動轉動副和動平臺的剛度遠大于連桿剛度，振動特性主要受3條支鏈影響，故在振動建模過程中忽略固定連接處的剛度及上下平臺結構剛度，重點考慮連桿特征參數。

考慮到所分析的并聯指向機構的運動為低速運動，其工作狀態下的自振頻率一般較低，且該機構對振動最為敏感的微動結構的垂直方向的振動相比其他方向更為顯著，因此本文對所建立的振動系統模型進行了一定程度的簡化，選擇垂直于動平臺的方向為關注的振動方向進行建模。

圖2 基于數軸法建立的機構振動模型Fig.2 Vibration model based on number axis method

在垂直于動平臺的方向上，基于數軸法建立了簡化后的3-RRCPR并聯指向機構振動模型，如圖2所示。圖中mi、ki、ci分別為系統的質量、剛度系數和阻尼系數，各個集中質量塊所代表的指向機構零部件見圖2中標注。R副表示轉動驅動副，P副表示移動驅動副。

機構振動系統微分方程為

(1)

式中，x為所建立的振動模型中各質量塊mi的廣義物理坐標的振動位移；M為質量矩陣；K為剛度矩陣；C為阻尼矩陣；F為振動方向上的外力。

利用圖2所示的基于數軸法所建立的振動模型，對質量矩陣M、剛度矩陣K和阻尼矩陣C進行構造并將其代入式(1)中，即可較為簡便地得到機構的振動模型。

構造的機構質量矩陣M和剛度矩陣K可以表示為

M=diag(m1+m11+m12+m13,m21,
m22,m23,m31+m32+m33+m3)

(2)

(3)

K1=k11+k12+k13K2=k11+k21

K3=k12+k22K4=k13+k23

K5=k21+k22+k23+k3

因為指向機構的阻尼主要是源自材料內的阻力和部件結合面之間的干摩擦[11]，所以選擇在機械結構振動分析中廣泛應用的瑞利阻尼。阻尼矩陣C可表示為

(4)

c11=α(m1+m11+m12+m13)+β(k11+k12+k13)
c12=-βk11c13=-βk12c14=-βk13
c22=αm21+β(k11+k21)c25=-βk21
c33=αm22+β(k12+k22)c35=-βk22
c44=αm23+β(k13+k23)c45=-βk23
c55=α(m3+m31+m32+m33)+
β(k3+k21+k22+k23)

其中，α、β分別為質量阻尼系數和剛度阻尼系數，可以根據某兩階固有頻率確定：

(5)

(6)

式中，ωi、ωj為某兩階固有頻率；ξi、ξj為與之對應的兩階模態振型阻尼比。

1.2 振動模型的正確性驗證

為驗證由式(1)～式(4)所構造的機構數軸法振動模型的正確性，需要利用此模型計算得到的固有頻率結果同有限元分析結果進行對比。根據指向機構各部位使用的材料，得到振動模型質量參數數值，如表1所示。

表1 振動模型質量參數

利用靜應力分析結合曲線擬合可得到振動模型剛度參數數值，如表2所示。

表2 振動模型剛度參數數值

令并聯指向機構振動系統在零初始條件下的初始速度和位移為零，則復平面上的振動響應方程為

(s2M+sC+K)X(s)=0

(7)

式中,s為振動方程經拉氏變換后的復變量；X(s)為廣義坐標的振動幅值和方向。

考慮到并聯機構的實際阻尼很小，對機構的模態特性影響也有限，本文針對無阻尼非線性振動系統進行分析。忽略式(7)中阻尼參數，并將表1、表2中數值代入式(2)所示質量矩陣和式(3)所示剛度矩陣中，可得無阻尼振動系統的特征方程：

|s2M+K|=0

(8)

進一步可得廣義特征方程：

KU=-s2MU

(9)

將矩陣M進行Cholesky分解，即

M=LLT

(10)

由于M為正定對角矩陣，可知L=LT。令A=L-1K，B=LT，可將求解式(8)的問題轉化為廣義特征值的求解問題：

L-1KU=-s2LTU

(11)

AU=s2BU

(12)

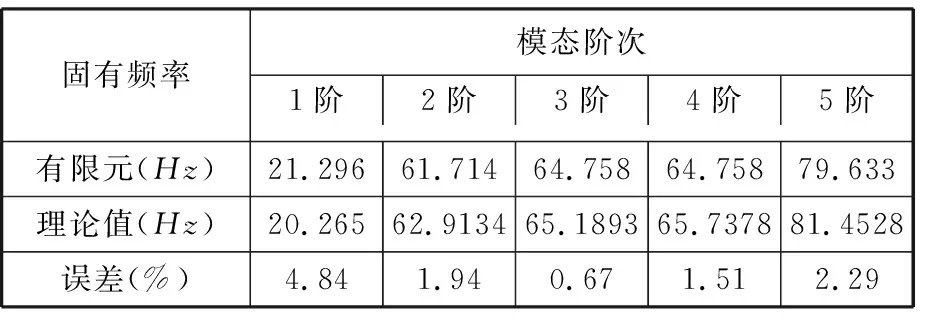
表3 理論模型模態參數計算精度

表3結果顯示，理論建模計算結果最大誤差不超過5%，符合工程精度要求，證明了該建模方法的可行性。

1.3 考慮殘余剛度的改進非線性等效剛度系數

若要將上文所建立的基于數軸法的理想機構振動模型拓展至考慮間隙的機構振動模型中，需要對含間隙運動副內的剛度系數進行定義。

目前研究含間隙運動副的相關文獻所使用的間隙接觸模型多為圖3所示的轉動副間隙模型，主要針對軸和軸套之間存在間隙ebj時的非線性剛度kn及法向接觸力FN進行研究，含間隙非線性剛度系數在軸與軸套之間發生接觸、分離及相互嵌入時，會呈現出多段函數的特征[12]，且以是否分離為邊界決定剛度系數是否為零，分離時軸與軸套互不接觸。

圖3 間隙副軸與軸套的接觸模型Fig.3 Contact and collision model of clearancecountershaft and bushing

對于并聯指向機構的振動模態特性分析，需考慮系統整體的剛度特性。振動模型中的剛度參數不僅需要考慮運動副內的接觸支撐剛度，還需要考慮該部位裝配特征對局部剛度產生的影響，如階梯軸支撐面、聯軸器的連接等，這些特征可能對間隙內零部件的相對運動產生一定程度的抑制，因此在運動副接觸部位由于間隙發生分離時，該處剛度并不會像傳統模型中定義的一樣為零，而是會出現一定程度的削弱，將此時的剛度定義為殘余剛度。因此上述間隙接觸等效模型需要進行改進，改進模型中軸套和軸的半徑差(即初始間隙)設為ΔR，隨機構運動時動態變化的軸套和軸的中心距離(即間隙值)設為δ。

由文獻[13]可知含間隙運動副內非線性接觸剛度系數

(13)

(14)

式中，l為兩間隙接觸面的長度；n為力指數；e為兩接觸面在接觸時的變形量，隨時間變化；E*為兩接觸面材料的等效彈性模量；ν1、ν2分別為兩接觸面材料的泊松比；E1、E2分別為兩接觸面材料的彈性模量。

令剛度系數ks為運動副接觸部位由于間隙發生分離時的殘余剛度，kε為間隙處兩接觸面之間發生接觸碰撞時的非線性接觸剛度系數，結合以上兩參數的多段函數作為改進后的非零含間隙非線性等效剛度系數ke：

(15)

1.4 考慮時變運動副間隙的機構振動系統建模

為了將運動副的間隙特征嵌入由式(1)～式(4)所構造的機構理想振動模型中，將含間隙運動副在圖2所示模型中的對應位置上添加間隙ΔR，并用式(15)所建立的考慮殘余剛度的非線性等效剛度系數ke代替原始常值剛度系數kr，例如若A支鏈連桿1、連桿2之間的從動轉動副含有間隙，則所構造的含間隙振動模型如圖4所示。

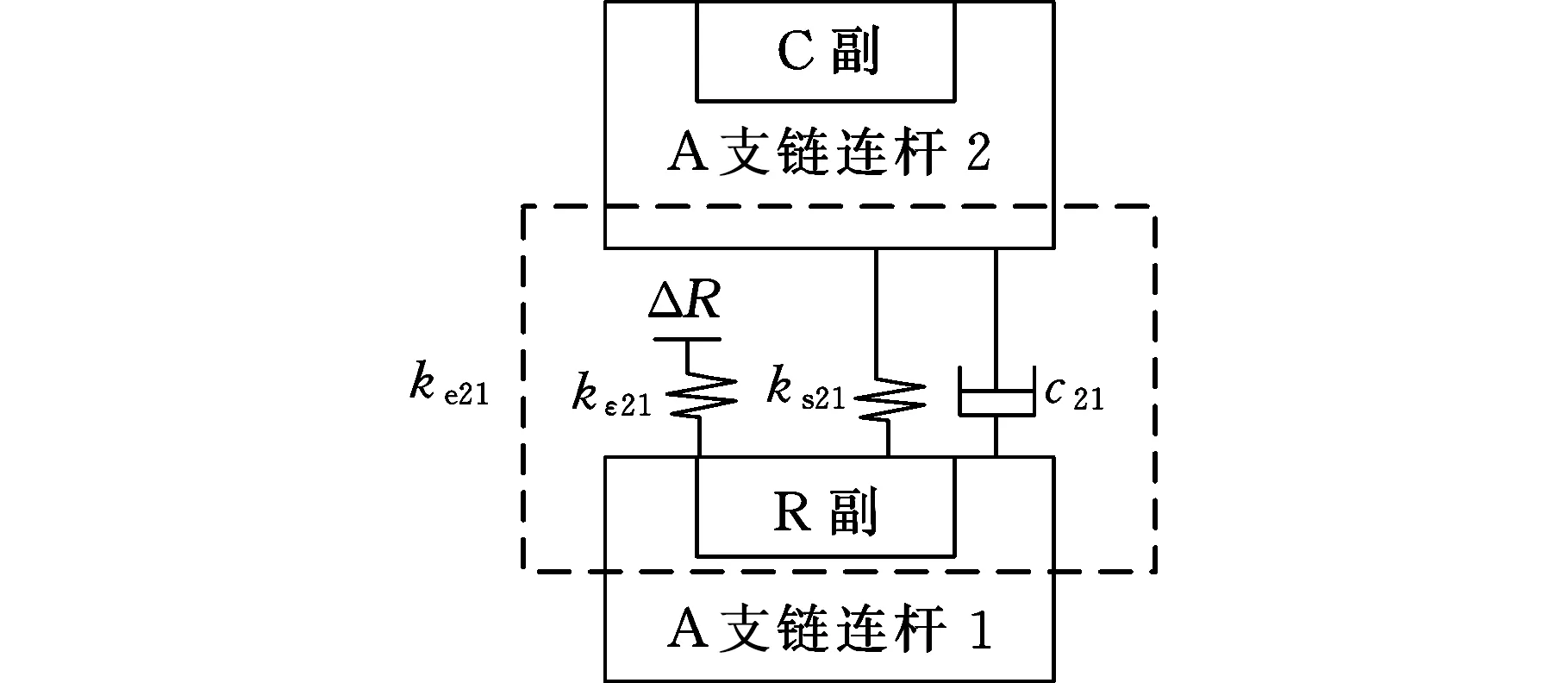
圖4 考慮運動副間隙的振動模型Fig.4 Vibration model considering the clearance ofthe kinematic pair

考慮運動副間隙的機構振動系統微分方程為

(16)

式中，Ks為含間隙振動系統的包含殘余剛度系數的總體剛度矩陣；FG為振動系統中由于間隙的存在而額外產生的內力[14]。

隨著振動系統中含間隙運動副內的間隙值δ的變化，非線性等效剛度系數ke也隨之變化，該系數中已包含了含間隙運動副的接觸特征，能表征接觸部位的任何時刻的剛度特性。將式(16)中的系統內力FG等效為εx，ε作為該振動系統中某些運動副存在間隙時整個振動系統剛度特征的表征符號，本文將其構造為如下形式的含間隙剛度矩陣Ke來對剛度特征進行描述(此處矩陣Ke與圖4模型相對應):

(17)

由式(16)和式(17)，考慮運動副間隙機構的振動系統微分方程可以表示為

(18)

并聯指向機構中含間隙運動副的類型及數量不同，式(18)所示的間隙剛度矩陣的參數構造也會有所不同，但構造原理和過程是相同的。

已知含間隙振動系統方程的特征多項式為

|s2M+Ke(e)|=0

(19)

綜上可建立考慮時變間隙的機構無阻尼非線性振動模型：

(20)

殘余剛度ks與原始剛度、間隙特征均有一定聯系，本文簡化為縮減一定比例的殘余剛度ks。

若考慮運動副間隙對阻尼的影響，與建立的改進非線性等效剛度系數類似，可以建立非線性等效阻尼系數 。殘余阻尼系數cs與間隙副內接觸面發生碰撞摩擦時的非線性阻尼系數cε[15]共同構成含間隙機構振動模型的非線性等效阻尼系數ce。振動系統中各項的阻尼系數cs及cε分別構成阻尼矩陣Cs及Cε，由Cs及Cε即可構造出非線性等效阻尼矩陣Ce。

Cs(cs)=αM+βKe(e)

(21)

(22)

(23)

式中，g為恢復系數，與材料本身的性質有關；v0為接觸碰撞前的速度。

進而可以建立考慮時變間隙的有阻尼機構振動模型：

(24)

2 考慮時變間隙的機構非線性模態分析

2.1 并聯指向機構間隙動力學仿真

若要分析考慮時變間隙的3-RRCPR并聯指向機構非線性模態特性，需要得到機構含間隙運動副內的間隙數據δ，這里通過ADAMS中建立的含間隙動力學模型并進行仿真分析來實現數據的獲取。

考慮到所分析機構的結構和負載特征，對存在間隙時的機構支鏈上連桿1和連桿2之間的從動轉動副以及基座上驅動轉動副進行動力學仿真分析，利用反饋控制力矩方式在間隙動力學仿真中模擬電機驅動；根據運動副的裝配特征設置仿真模型的間隙運動副連接；調整間隙運動副的接觸碰撞參數以盡可能減少接觸碰撞的失真；在最容易發生振動的滾珠花鍵處參考日本THK公司LF系列滾珠花鍵的參數設置摩擦參數。這些設置使仿真模型盡可能符合工程實際。由于現階段對復雜并聯指向機構進行含間隙動力學實驗時在成本和實現難度等方面還存在較大問題，尤其是變化的間隙特征難以在實驗中進行實時測量，因此通過理論模型結合間隙動力學中已有大量應用的ADAMS仿真工具對機構非線性模態進行研究，可以為這類問題的研究提供一定理論依據。間隙動力學仿真模型如圖5所示。

(a)并聯指向機構仿真模型

仿真條件設置如下：A支鏈驅動轉動副轉速10°/s，驅動時間5 s，即驅動轉角0°～50°，設置驅動轉動副間隙為0～0.5 mm，第1、第2連桿之間的從動轉動副間隙為0～5mm，分別對存在不同間隙特征的機構進行間隙動力學仿真。

由于本文分析所得到的機構含間隙動力學仿真間隙數據圖較多，故僅以機構A支鏈的驅動轉動副出現0.1 mm間隙且驅動轉速為10°/s時情況為例進行展示，并聯指向機構的含間隙運動副內位移如圖6所示。

圖6 指向機構含間隙驅動轉動副內位移Fig.6 Pointing mechanism with clearance drive andinternal collision displacement of rotating pair

2.2 改進的非線性等效剛度系數ke求解

通過ADAMS仿真可以得到式(15)中的非線性等效剛度系數ke中的間隙位移參數δ，其他參數如表4所示。

表4 非線性接觸剛度系數kε的已知參數

由表4中的參數結合式(14)可求得接觸面材料的等效彈性模量E*為113.5 GPa。根據式(15)，在MATLAB中建立對應的數學模型，并將機構中含間隙運動副的對應剛度系數設置為變量，然后將ADAMS仿真得到的間隙數據作為數值矩陣導入該數學模型中，結合式(13)、式(14)求得非線性等效剛度系數ke。圖7、圖8所示為當A支鏈驅動轉動副和從動轉動副分別出現0.1 mm、0.2 mm和0.3 mm的間隙時，間隙副內非線性等效剛度系數的變化情況。

圖7 含間隙驅動副非線性等效剛度系數變化Fig.7 Nonlinear equivalent stiffness coefficient changeof driving pair with gap

圖8 含間隙從動副非線性等效剛度系數變化Fig.8 Variation of nonlinear equivalent stiffnesscoefficient of driven pair with gap

并聯指向機構的驅動轉動副固定于基座上，空間位置不隨機構運動變化，故間隙副內碰撞運動主要受重力、間隙值和轉速因素的影響。由圖7、圖8可知，當轉速為10°/s時，隨著驅動轉動副間隙值的增大，含間隙非線性等效剛度瞬時突變峰值有所衰減；從動轉動副由于位于連桿連接處，空間位置會隨連桿運動發生變化，此時相比于轉動副間隙值的大小，重力和連桿空間交錯位置會對間隙副內碰撞運動產生更為顯著的影響，在一定轉速下連桿轉角處于0°～10°和30°～50°時非線性等效剛度突變峰值較大，明顯出現相較于10°～30°區域更激烈的接觸碰撞。

2.3 含間隙并聯指向機構模態特性分析

將上文求解得到的非線性等效剛度系數代入形如式(17)的含間隙剛度矩陣中，有

Ke(e)=K(ks,kε(e))

(25)

而在q個時刻內，隨著間隙變化的時變非線性等效剛度系數可構成數組{ke}q，將其代入含間隙剛度矩陣式(17)中，則可得三維含間隙剛度矩陣：

(26)

將此矩陣代入式(20)所示的考慮時變間隙的無阻尼非線性振動模型中，即可求解時變模態固有頻率。將運動副出現不同間隙值時指向機構的時變模態固有頻率進行整合，即可得到機構的模態固有頻率分布域。

本文針對在A支鏈驅動轉動副0°～50°轉動范圍內，驅動轉動副以及第1連桿、第2連桿之間的從動轉動副分別出現0～0.5 mm的間隙，以及支鏈上的驅動轉動副和從動轉動副同時出現0～0.5 mm的間隙時，機構的非線性模態固有頻率分布域進行了分析，其結果見圖9～圖11。

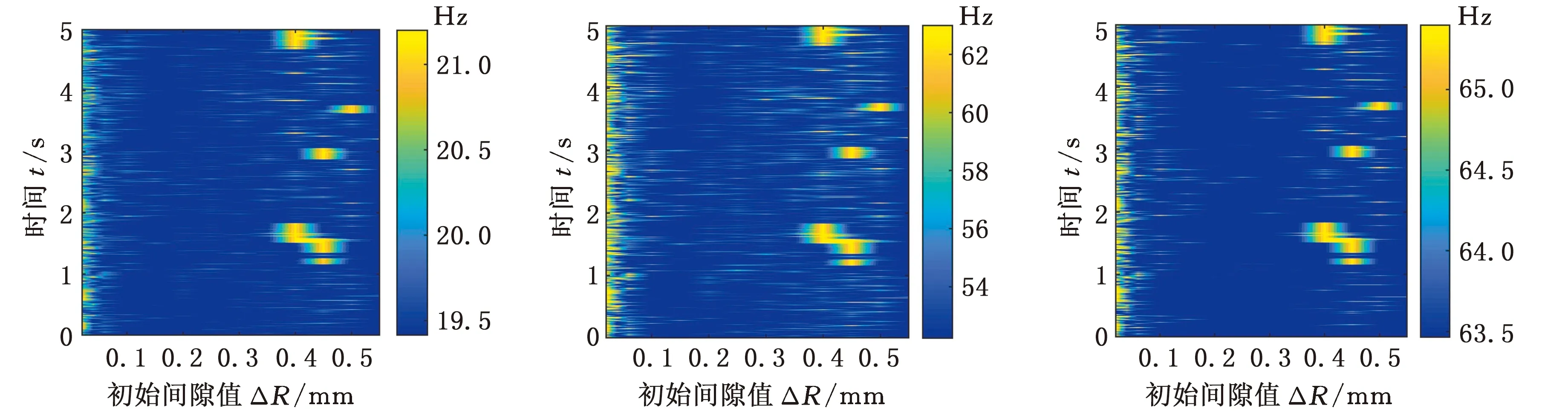
(a)1階固有頻率 (b)2階固有頻率 (c)3階固有頻率

(a)1階固有頻率 (b)2階固有頻率 (c)3階固有頻率

(a)1階固有頻率 (b)2階固有頻率 (c)3階固有頻率

由圖9～圖11可知，驅動轉動副和從動轉動副的不同間隙值對并聯指向機構非線性模態產生的影響有明顯不同。驅動轉動副間隙的存在會使固有頻率出現短時間內的劇烈突變，這種現象在間隙值為0.4～0.5 mm時尤為明顯；從動轉動副間隙則會使固有頻率出現較為均勻的波動，且在機構轉角較大時更加明顯；當兩種間隙同時存在時，產生的耦合效應又會使頻率分布域呈現不同的特點，可以較為直觀地看出除了第2階固有頻率之外的幾階波動都明顯減弱。

為了更為直觀地了解含間隙運動副對指向機構模態固有頻率的影響，依據圖9～圖11整理了如圖12和表5所示的并聯指向機構模態固有頻率波動范圍圖。

圖12 不同間隙特征影響下模態固有頻率波動Fig.12 The modal natural frequency fluctuation underthe influence of different gap characteristics

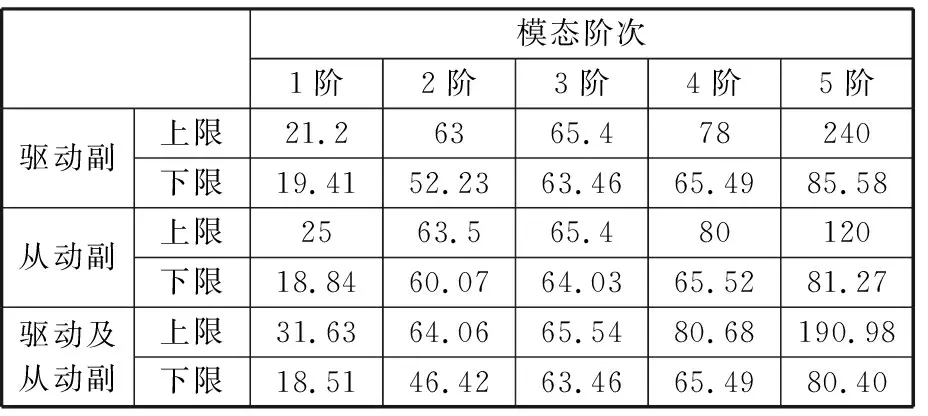
表5 模態固有頻率波動上下限

分析圖9～圖12和表5可知，并聯指向機構運動副存在0～0.5 mm間隙時，含間隙運動副的非線性等效剛度的瞬時變化會使機構模態固有頻率發生波動。驅動副間隙影響下模態分布域波動較為均勻，大范圍波動集中在間隙0～0.1 mm和0.4～0.5 mm處；從動副間隙影響下模態分布域波動主要集中在機構初始位置和第1連桿30°～50°轉動范圍內；機構的驅動轉動副和從動轉動副同時出現間隙時，機構的第1和第3～第5階模態固有頻率的分布域波動會大大減弱，幾乎只存在于間隙值0～0.1 mm范圍內，只有第2階模態固有頻率分布域仍然存在明顯的均勻波動，且對第1、2階模態頻率的波動上下限影響也明顯增大，波動上限增加了5～6 Hz，而對5階模態頻率的上下限影響與單驅動副間隙時相比有所降低，分析后判斷是由于多個間隙的耦合使得支鏈的柔度有所增加，機構的高頻振動得到一定抑制，低頻高振幅的振動影響更加顯著，這會使得機構各階固有頻率分布域尤其是第1階的波動次數明顯降低，但第1、2階波動的幅度會有所提高。

理論模型計算的5階模態中，第5階模態對運動副間隙較為敏感，在發生接觸時，頻率波動可達40～150 Hz，且驅動副間隙對模態固有頻率的影響與從動副相比更為顯著；第1～第4階模態在不同運動副間隙特征的影響下波動范圍較小，整體不高于15 Hz。這說明機構在低階工作頻率下具有較好的穩定性。

3 結論

(1)3-RRCPR并聯指向機構單個支鏈的驅動轉動副在0°～50°轉角范圍內，驅動轉動副出現間隙時，機構的非線性模態固有頻率會出現較為均勻的時變波動，且在間隙值為0～0.1 mm、0.4～0.5 mm時波動較為明顯；從動轉動副出現間隙時，會使機構固有頻率在初始位置和連桿30°～50°轉動范圍內出現較為頻繁的波動；驅動副和從動轉動副同時出現間隙時，機構第2階之外的模態固有頻率波動頻繁程度會明顯降低，但是第1、第2階的波動上下限會出現5～15 Hz的變化；機構的第5階模態固有頻率對運動副間隙的敏感度遠大于第1～第4階，其波動值至多是第1～第4階模態的數10倍，這說明在并聯指向機構某一從動副、驅動副或兩者同時出現間隙時，機構的1～4階固有頻率數值不會發生過大的突變，也說明了在低頻域下運轉時該機構具有較好的穩定性。

(2)本文的研究內容可以為所分析的3-RRCPR機構的動態性能優化、結構共振域分析、故障預測等供理論分析依據，也可以為其他復雜機構的振動模態建模分析提供一種可行的研究方法和思路。