CT圖像重建中的一種新型濾波器

楊坪坪，馮漢升，許繼偉，宋云濤，

1.中國科學技術大學，安徽合肥230026；2.中國科學院等離子體物理研究所，安徽合肥230031；3.中科離子醫學技術裝備有限公司，安徽合肥230088

前言

隨著計算機斷層成像技術（CT）在醫學成像、工業無損檢測、地球勘探等領域應用愈加廣泛，人們對CT 成像質量要求越來越高［1‐2］。重建算法［3‐7］一直是CT技術的核心，其主要分為解析算法和迭代算法，其中解析算法以濾波反投影（Filtered Back Projection,FBP）算法為主，相較迭代算法，解析算法耗時明顯更少，因此商業應用更加廣泛。就解析算法中的FBP算法而言，其實現主要分為濾波、反投影重建兩步，其中濾波器的設計對重建圖像質量起著關鍵作用。常見的濾波器有RL 濾波器和SL 濾波器等［8‐11］，但均各有不足。RL濾波器采用矩形窗對斜坡濾波器進行截取，有明顯的Gibbs 現象，表現為嚴重的振蕩效應。SL 濾波器采用sinc 窗函數對斜坡濾波器進行截取，振蕩現象減弱，但因其低頻段偏離斜坡函數，因此低頻段重建質量不如RL 濾波器。此外文獻［12］指出，通過加權因子的選擇，一次指數濾波器能達到RL 濾波器、SL 濾波器相似的效果，其性能效果是RL濾波器、SL濾波器的折中。本文通過對一次指數濾波器的研究引入高斯濾波器，并進一步設計了一種新型濾波器——改進高斯濾波器，從濾波器設計原理出發，通過仿真實驗結果對比分析驗證了該濾波器在有無噪聲的情況下，都能很好地抑制圖像灰度波動，同時能有效改善重建圖像質量，重建性能表現優越。

1 原理介紹

1.1 FBP算法

FBP 重建算法可分為二維圖像重建與三維圖像重建，但其濾波器設計是通用的。FBP算法中的濾波步驟主要是為了消除反投影圖像中存在的星狀偽影。研究指出星狀偽影可以在反投影重建之前進行濾波消除，其濾波實現較先反投影后濾波更為簡單，稱為FBP 算法［2］。FBP 算法具體實現步驟（以二維圖像重建為例）為：

（1）對某一個角度下的投影數據pθ(t)作一維傅里葉變換，記為Pθ(w)：

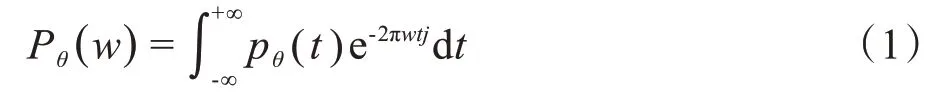
（2）對Pθ(w)進行一維斜坡濾波器H(w)=|w|濾波，記為P'θ(w)：

（3）對P'θ(w)進行傅里葉逆變換，記為p'θ(t)：

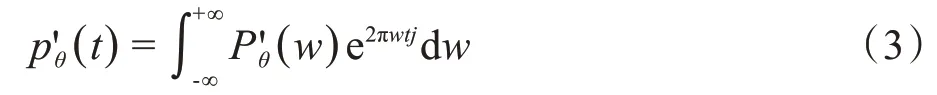
（4）對濾波后的投影圖像（0°到180°的投影圖像）作反投影累加加權，得到重建圖像f(x,y)：

1.2 濾波器設計

理論上濾波器H(w)=|w|是一個無限頻帶的濾波函數，無法實現［13‐14］。但在實際成像過程中，投影數據高頻分量比較小，且投影過程（X射線成像過程）中有平均作用，相當于低通濾波，因此可以采用濾波窗函數對斜坡函數在截止頻率（，其中d為探測器間距）范圍內進行加窗［15］，如下：

因此，濾波器設計實際上是窗函數選取的過程。判斷窗函數的優劣一般有3個指標：主瓣、近旁瓣、遠處旁瓣。窗函數的選擇一般要求主瓣高而窄，空間分辨率越高，最大旁瓣相對主瓣盡可能幅度小，數值精度越高，密度分辨率越高，同時遠旁瓣幅度與幅值小，曲線過渡平滑，以防止嚴重的Gibbs現象［16‐17］。

1.3 一次指數濾波器

文獻［12］指出，一次指數濾波器能通過加權方式達到與RL 濾波器、SL 濾波器相似的效果，其形式如式（6）所示。

其中，a為加權因子，B為截止頻率。通過選擇不同的加權因子，一次指數濾波器能達到不同的效果。

文獻指出，當a取0.64 時，其效果類似于SL 濾波器，其頻域曲線［18］、空域曲線［19］如圖1和圖2所示。

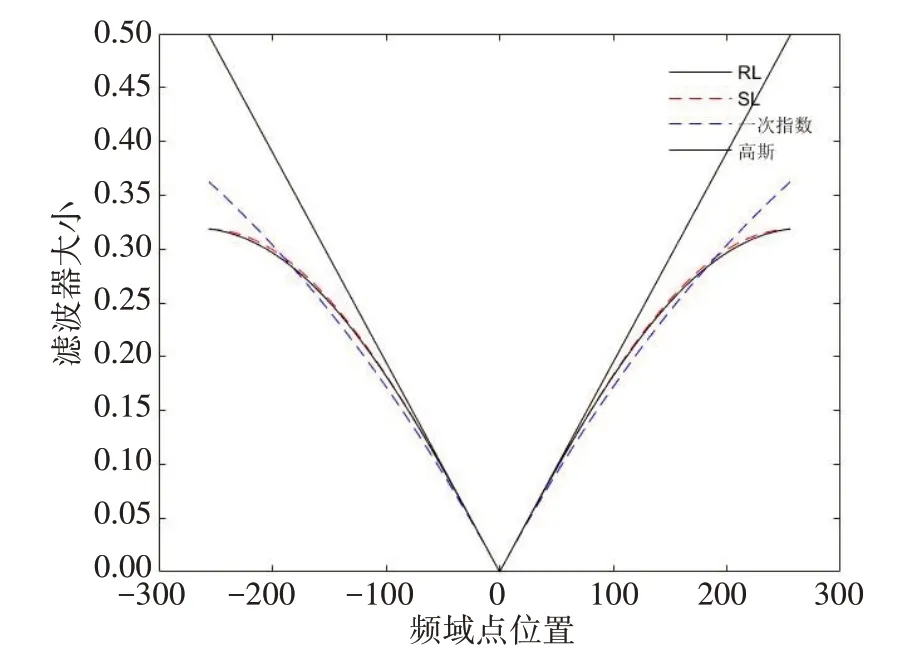
圖1 一次指數函數a=0.64，高斯函數k = 1.8與SL、RL函數頻域對比Fig.1 First-order exponential function a=0.64,Gaussian function k=1.8,compared with SL and RL functions in the frequency domain

圖2 一次指數函數a=0.64，高斯函數k = 1.8與SL、RL函數空域對比Fig.2 First-order exponential function a=0.64,Gaussian function k=1.8,compared with SL and RL functions in the space domain

從圖1、圖2中可明顯看到，當一次指數濾波器權值a=0.64 時，其頻域曲線近似直線，與RL 濾波器更相似，其空域曲線存在明顯的振蕩，頻域曲線截止頻率附近沒有明顯壓低，因此會存在明顯的Gibbs 效應，并且對高頻噪聲十分敏感。據此，引入高斯濾波器，其形式如下：

式中，k為加權因子。當k=1.8 時，其頻域曲線與空域曲線見圖1、圖2。可以明顯看出，高斯濾波器通過加權能更加逼近于SL濾波器，空域曲線光滑，沒有出現明顯的振蕩現象，頻域曲線截止頻率附近較一次指數濾波器明顯壓低，能有效抑制Gibbs現象。且當k=0時，高斯濾波器等同于RL 濾波器，因此高斯濾波器實際應用效果是RL、SL 濾波器的折中。為了進一步驗證高斯濾波器相比一次指數濾波器的優良性，后文將會采用仿真實驗對比驗證。

2 改進高斯濾波器

為了進一步改進高斯濾波器，本文設計了新型濾波器——改進高斯濾波器，其形式如下：

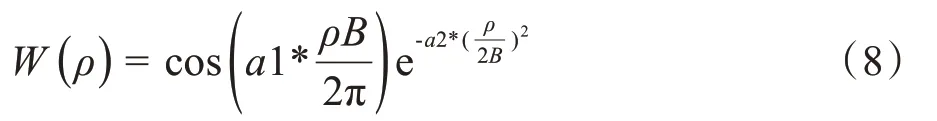
式中，a1、a2為加權因子。可以看出，當a1= 0時，改進高斯濾波器退化為高斯濾波器。其中a1加權因子的引入是為了實現對高斯濾波器截止頻率附近的進一步壓低以減小Gibbs 效應以及噪聲影響，其加權因子對比頻域曲線見圖3。

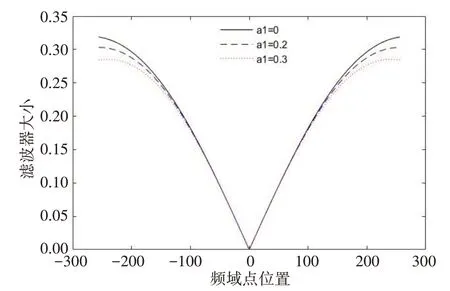
圖3 a2=1.8時，a1取0、0.2、0.3時改進高斯濾波器頻域對比圖Fig.3 Comparison of the frequency domain of the improved Gaussian filter when a1=0,0.2 and 0.3,with a2=1.8

更進一步，本文做了針對不同加權因子的剖線灰度曲線對比圖，其參數與后文的重建參數一致。灰度曲線表征了圖像的粗糙程度，曲線波動越大，圖像越粗糙。從圖4中可以看出，當a1 給定時，a2 越大圖像越平滑，能更好地還原原始模型。

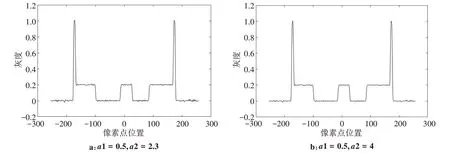
圖4 a1= 0.5,a2取2.3、4.0時的灰度曲線對比Fig.4 Comparison of grayscale curve when a2=2.3 and 4.0,with a1=0.5

為了進一步驗證實驗結果評價圖像質量，引入常用的醫學圖像判據，其形式如下：

（1）歸一化均方距離d：

式中，tx,y、rx,y分別表示模型原圖和重建圖對應點的像素密度，t'表示模型原圖密度的平均值，圖像像素N×N個。歸一化均方距離表征了少數點的大誤差情況。

（2）歸一化平均絕對距離r：

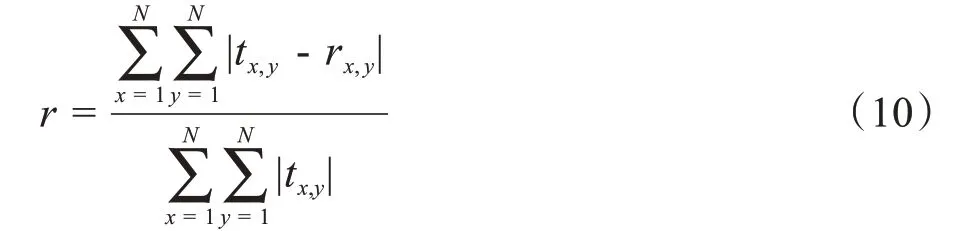
歸一化平均絕對距離表征了多數點的小誤差情況。

從表1可以看出，a2 越大圖像越平滑，但相應的重建誤差將會增大，其中歸一化均方距離誤差明顯升高。因此實際重建過程中，需要根據需求靈活選擇加權因子。

表1 a1= 0.5,a2取2.3、4.0時改進高斯濾波器的重建誤差對比Tab.1 Comparison of reconstruction error of the improved Gaussian filter when a2 = 2.3 and 4.0,with a1=0.5

3 改進高斯濾波器仿真實驗對比

為了測試改進高斯濾波器實際應用效果，對濾波器在無噪聲情況與加噪聲情況下的重建過程進行模擬實驗驗證。其中重建模型采用二維Shepp‐Logan圖像［20］，重建模式選用二維平行束重建，投影角度取0°到179°，步長為1，重建圖像大小為512×512，探測器采樣點數512，重建像素間隔與探測器采樣間隔均取1 mm。分別取無噪聲與有噪聲情況下的重建結果圖，灰度曲線圖與重建誤差表（分別為歸一化均方距離誤差表與歸一化平均絕對距離誤差表）進行對比，其中灰度曲線圖采用像素位置256處的重建圖像橫向剖線，一次指數濾波器權值取0.64，高斯濾波器權值取1.8，改進高斯濾波器權值a1=0.5，a2=2.3。

3.1 無噪聲情況下不同濾波器重建結果與相應的灰度曲線圖

通過圖5與表2可以發現，一次指數濾波器重建效果與RL 濾波器相似，灰度曲線波動很大，圖像粗糙，重建誤差也很大。高斯濾波器重建效果與SL 濾波器相似。改進高斯濾波器灰度曲線相比其他濾波器明顯更平滑，其重建誤差明顯減小，歸一化均方距離與SL 濾波器差距不大，其歸一化平均絕對距離卻比SL濾波器小許多。因此，在無噪聲情況下，改進高斯濾波器重建結果明顯優于其他濾波器。

表2 不同濾波器重建誤差表Tab.2 Reconstruction errors of different filters

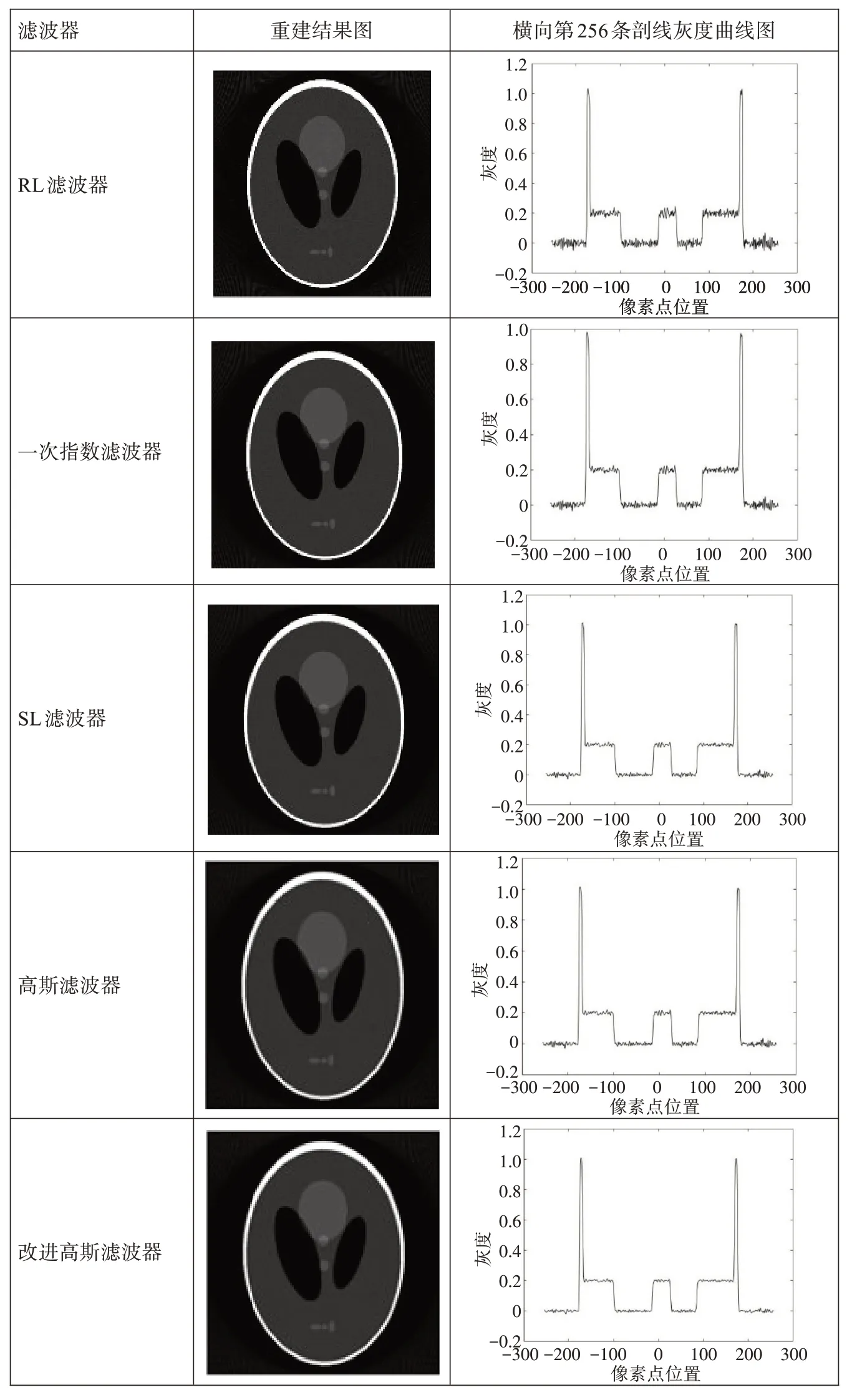
圖5 無噪聲情況下不同濾波器重建結果與相應的灰度曲線圖Fig.5 Reconstruction results of different filters in the case of noise-free and the corresponding grayscale curves

3.2 有噪聲情況下不同濾波器重建結果與相應的灰度曲線圖

從圖6可以看出，在有噪聲情況下，一次指數濾波器重建灰度曲線圖略優于RL濾波器，且明顯劣于SL濾波器、高斯濾波器與改進高斯濾波器，因此重建圖像非常粗糙。高斯濾波器重建灰度曲線較SL濾波器更平滑。改進高斯濾波器重建灰度曲線較其他濾波器波動明顯更小，更加趨近于原始圖像。

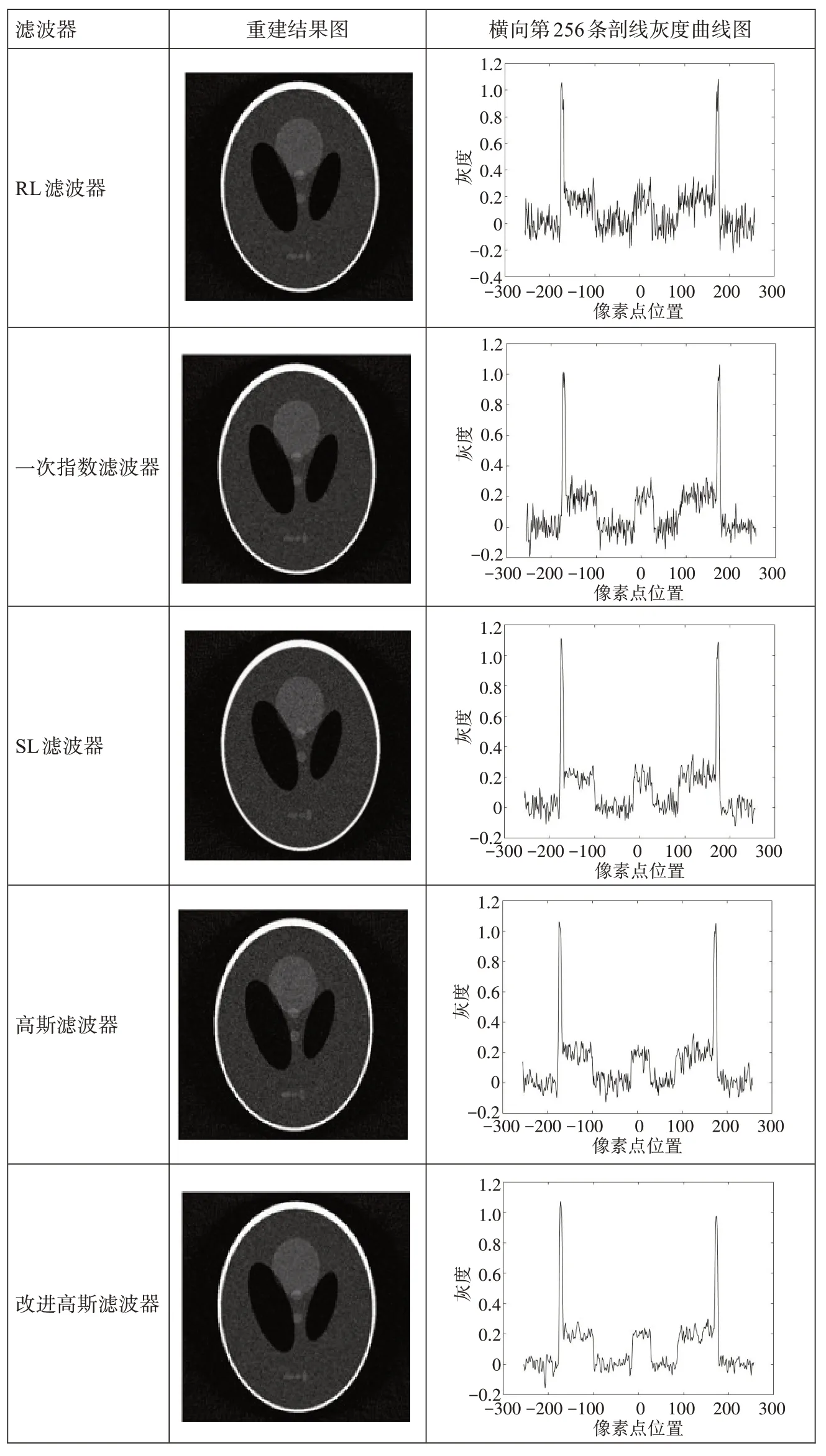
圖6 有噪聲情況下不同濾波器重建結果與相應的灰度曲線圖Fig.6 Reconstruction results of different filters in case of noises and the corresponding grayscale curves

為了進一步驗證改進高斯濾波器的抗噪性能，采用抗噪性能明顯優于RL 濾波器的SL 濾波器進行對比，做了3 組噪聲對比實驗，加噪噪聲采用平均值為0、方差為1 的不同強度高斯噪聲進行對比，產生噪聲命令如下：

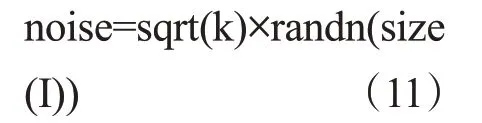
其中，k為參數，I為原始圖像，noise為噪聲圖像，randn能根據圖像大小產生標準正態分布序列。因此可以通過選取不同k值達到模擬不同噪聲強度的目的。

從表3、表4可以看出，改進高斯濾波器在不同噪聲強度下保持重建歸一化均方距離誤差相差不大的情況下，其歸一化平均絕對距離誤差明顯更小，因此擁有比SL濾波器更優的抗噪性能。

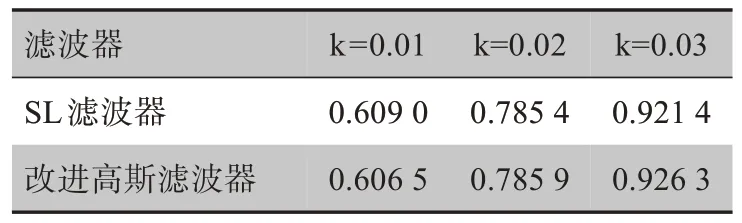
表3 SL濾波器、改進高斯濾波器在不同噪聲強度下的重建歸一化均方距離Tab.3 Reconstruction normalized mean square distances of SL filter and improved Gaussian filter under different noise intensities

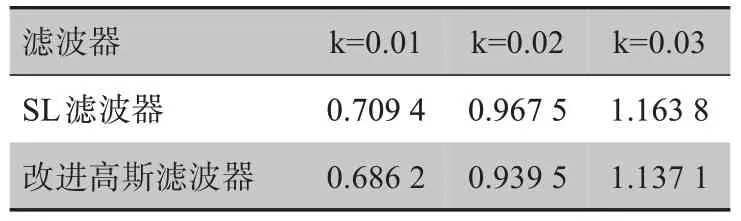
表4 SL濾波器、改進高斯濾波器在不同噪聲強度下的重建歸一化平均絕對距離Tab.4 Reconstruction normalized average absolute distances of SL filter and improved Gaussian filter under different noise intensities

4 結論

本文從已有對指數濾波器的研究出發，分析了一次指數濾波器的不足，引入高斯濾波器，并進一步改進提出一種新型濾波器。通過仿真實驗對比分別驗證了該濾波器較RL 濾波器、SL 濾波器、一次指數濾波器、高斯濾波器的優良特性，它有效抑制了重建時的灰度波動，重建圖像更加平滑，且在有無噪聲的情況下，均能保持更佳的重建圖像質量，重建誤差明顯更小。此外，在改進高斯濾波器加權因子選擇a1=0.5、a2=2.3 時，該濾波器能在有效保持圖像平滑的同時減小重建誤差。