基于支持向量機(jī)的氣壓輔助掘進(jìn)條件下盾構(gòu)隧道地表變形預(yù)測研究
李方毅,張曉平, *,許 丹,姜 軍,周 智,沈 婕,王浩杰,張心悅
(1. 武漢大學(xué)土木建筑工程學(xué)院,湖北 武漢 430072; 2. 中鐵十一局集團(tuán)有限公司,湖北 武漢 430061; 3. 中鐵建華南建設(shè)有限公司,廣東 廣州 511458; 4. 廣州地鐵集團(tuán)有限公司,廣東 廣州 510330)
0 引言
全斷面機(jī)械化盾構(gòu)隧道施工方法以掘進(jìn)速度快、機(jī)械化程度高、安全性能好、對環(huán)境影響小等顯著優(yōu)點逐漸成為城市地鐵隧道施工的主流方法。采用盾構(gòu)法進(jìn)行地鐵隧道施工過程中,難免會對周圍地層產(chǎn)生擾動,進(jìn)而誘發(fā)地表變形。當(dāng)變形超過一定限度時,極易對隧道、周邊建(構(gòu))筑物以及地下淺埋管線等造成不同程度的損傷破壞,誘發(fā)工程安全事故。因此,在盾構(gòu)隧道施工過程中,選擇合適的方法合理預(yù)測地表變形,進(jìn)而提前采取加固措施,對有效防止過大地表變形造成重大工程安全事故顯得尤為必要。
眾多學(xué)者采用經(jīng)驗公式法[1-2]、理論分析法[3-4]、數(shù)值模擬法[5-6]等多種方法對盾構(gòu)掘進(jìn)誘發(fā)地表變形進(jìn)行了研究。但經(jīng)驗公式法缺乏理論基礎(chǔ),無法將不同工況與經(jīng)驗公式聯(lián)系起來; 而理論分析法和數(shù)值模擬法無法考慮現(xiàn)場工程地質(zhì)條件和人工作業(yè)環(huán)境的高度復(fù)雜性,在計算參數(shù)選取方面存在固有缺陷。近年來,以人工智能為代表的盾構(gòu)掘進(jìn)誘發(fā)地表變形預(yù)測模型,以其在有效捕捉地表變形量與相關(guān)影響因子之間非線性關(guān)系方面的顯著優(yōu)勢,已經(jīng)逐漸成為預(yù)測盾構(gòu)掘進(jìn)誘發(fā)地表變形的有效手段[7]。孫鈞等[8]使用人工神經(jīng)網(wǎng)絡(luò)對隧道開挖引起的地表沉降進(jìn)行預(yù)測,論證了該方法的可行性和適用性。Suwansawat等[9]考慮隧道幾何因素、地質(zhì)因素、盾構(gòu)運行因素等影響因素,使用人工神經(jīng)網(wǎng)絡(luò)成功預(yù)測最終變形量。田執(zhí)祥等[10]認(rèn)為人工神經(jīng)網(wǎng)絡(luò)在樣本有限時預(yù)測精度不高,提出了基于支持向量機(jī)(SVM)的隧道變形預(yù)測方法。
支持向量機(jī)與人工神經(jīng)網(wǎng)絡(luò)相比,有效克服了神經(jīng)網(wǎng)絡(luò)易陷入局部最小值而非全局最小值的固有缺陷[11]。但目前支持向量機(jī)的超參數(shù)(如懲罰參數(shù)c和核函數(shù)參數(shù)g)選擇大多通過反復(fù)試驗獲得,試錯過程復(fù)雜,且難以保證得到最優(yōu)結(jié)果。潘宇平等[12]使用交叉驗證法獲取了支持向量機(jī)超參數(shù)組合,但存在耗時過長等不足。Zhang等[13]使用粒子群算法優(yōu)化支持向量機(jī)超參數(shù),并對比分析了多種預(yù)測方法性能,但其研究中所使用的訓(xùn)練數(shù)據(jù)與預(yù)測數(shù)據(jù)均為隨機(jī)選取,難以指導(dǎo)盾構(gòu)隧道工程現(xiàn)場施工。袁志明[14]使用粒子群算法優(yōu)化支持向量機(jī)超參數(shù),預(yù)測了地鐵基坑開挖導(dǎo)致的變形。俞俊平等[15]則使用PSO-SVM模型預(yù)測了邊坡變形。但目前尚未有針對氣壓輔助掘進(jìn)條件下的盾構(gòu)隧道地表變形預(yù)測模型。
本文引入粒子群算法(PSO)對支持向量機(jī)(SVM)超參數(shù)進(jìn)行優(yōu)化,建立PSO-SVM預(yù)測模型。針對氣壓輔助掘進(jìn)工法特點,考慮上覆黏土層厚度,優(yōu)化輸入?yún)?shù),并改進(jìn)上覆非均質(zhì)土層模型參數(shù)計算方法。以廣州地鐵18號線隴枕出入場線為例,采用已掘進(jìn)區(qū)間隧道地表變形數(shù)據(jù)對PSO-SVM模型進(jìn)行訓(xùn)練,進(jìn)而對未掘進(jìn)區(qū)間隧道地表變形進(jìn)行預(yù)測,并將預(yù)測結(jié)果與PSO-BP模型和SVM模型預(yù)測結(jié)果進(jìn)行對比分析,以期為后續(xù)氣壓輔助掘進(jìn)條件下的盾構(gòu)隧道變形預(yù)測提供理論依據(jù)和技術(shù)支撐。
1 PSO-SVM預(yù)測模型
1.1 支持向量機(jī)原理
支持向量機(jī)是根據(jù)廣義超平面理論,把樣本點從低維空間映射到高維空間,在高維空間內(nèi)進(jìn)行線性回歸,進(jìn)而得到在原低維空間的非線性回歸方法[16]。支持向量機(jī)目標(biāo)為找到一個偏差為ε的函數(shù)fsv(x)。
(1)
式中:φ為權(quán)值矢量;x為輸入矢量;i為矢量個數(shù),i=1,2,…,n(n為輸入個數(shù));xi∈Rn為對應(yīng)輸出值;yi∈R;K為核函數(shù);b為閾值;ε為偏差。
支持向量機(jī)常用的核函數(shù)有多項式核函數(shù)、徑向基核函數(shù)和sigmoid核函數(shù)等,本文采用徑向基核函數(shù),如式(2)所示。
(2)
式中σ為徑向基核函數(shù)的寬帶。
1.2 粒子群算法
粒子群算法(PSO)是一種受鳥類捕食行為啟發(fā)所開發(fā)的算法[17],算法首先初始化粒子群位置向量和速度向量,利用初始位置向量計算初始適應(yīng)度值,然后通過迭代更新粒子位置與速度向量找到最佳適應(yīng)度值。粒子速度和位置更新公式如式(3)和式(4)所示:
(3)
(4)
式(3)—(4)中:i表示第i個粒子;k為迭代次數(shù);Xi為位置向量;Vi為速度向量;c1和c2為非負(fù)的常數(shù),稱之為加速度因子;r1和r2為分布在[0,1]之間的隨機(jī)數(shù);ω為慣性權(quán)重;Pt為單個粒子的個體最優(yōu)極值;Pg為所有粒子的全局最優(yōu)極值。
1.3 PSO-SVM預(yù)測模型
本文引入粒子群(PSO)算法來優(yōu)化支持向量機(jī)(SVM)模型懲罰參數(shù)c和核函數(shù)參數(shù)g,使用這2個參數(shù)值代替粒子群算法中的位置向量。更新粒子群并通過適應(yīng)度函數(shù)計算適應(yīng)度值,迭代之后輸出最優(yōu)適應(yīng)度值,以該適應(yīng)度值下的參數(shù)組合作為SVM的參數(shù)來構(gòu)建最優(yōu)模型。

(5)
式中:n為每個子集中的樣本數(shù);ai為實測值;f(bi)為模型預(yù)測值;j表示第j個子集;k為子集個數(shù)。
2 模型輸入?yún)?shù)優(yōu)化
2.1 氣壓輔助掘進(jìn)工法
在土壓平衡盾構(gòu)掘進(jìn)中,若上覆土層氣密性較好,為提高掘進(jìn)效率,控制地表變形,可采用氣壓輔助掘進(jìn)工法,即在保持盾構(gòu)土艙壓力恒定的前提條件下,通過土艙頂部的注入孔向土艙內(nèi)注入壓縮空氣,使得土艙上部內(nèi)形成穩(wěn)壓的氣室,通過氣壓和土壓共同作用來平衡隧道掌子面水土壓力,如圖1所示。在實際掘進(jìn)過程中,碴土界面大約保持在土艙高度1/2處。
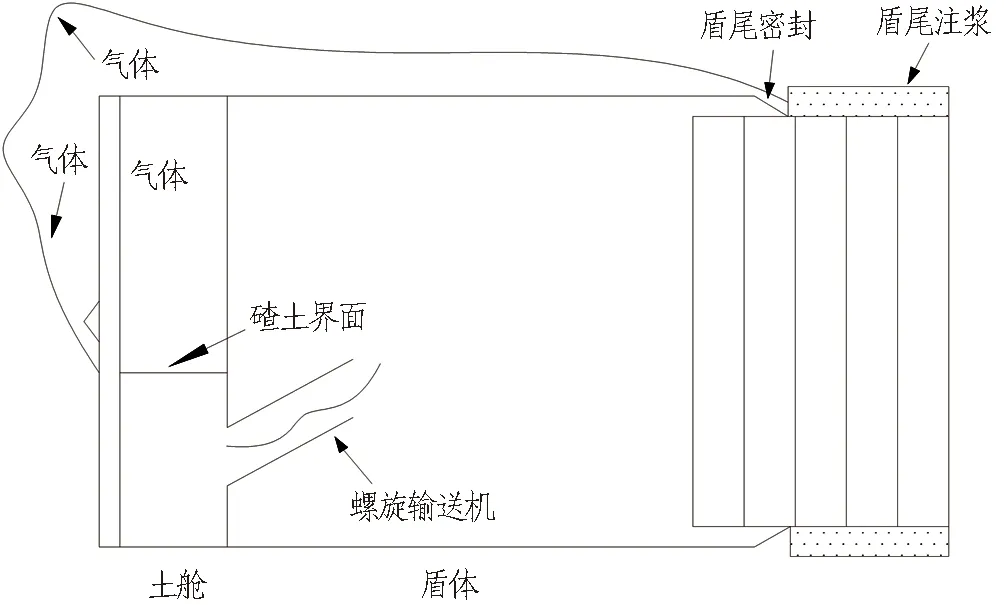
圖1 氣壓輔助掘進(jìn)工法示意圖
氣壓輔助掘進(jìn)主要有以下優(yōu)點: 1)氣壓作用于掌子面,可以防止掌子面前方及上部地下水進(jìn)入艙內(nèi),減少地下水流失,防止噴涌,有利于控制地表變形; 2)由于艙內(nèi)碴土量少,氣壓減磨效果顯著,可以充分減小刀盤轉(zhuǎn)矩,減小總推力,降低刀具磨損; 3)可以有效防止刀盤結(jié)泥餅,保證掘進(jìn)效率; 4)由圖1可知,氣壓還會作用于盾尾同步注漿處,壓實漿液,提高注漿質(zhì)量。
但目前氣壓輔助掘進(jìn)主要存在2個問題: 1)地層氣密性對氣壓保持影響較大。目前認(rèn)為該方法適用于上覆土層為粉砂質(zhì)、黏土等氣密性較好的土層,在砂礫、砂質(zhì)等氣密性較差的地層中保氣效果較差。氣密性較好的土層厚度也會影響氣壓穩(wěn)定效果,若黏土層厚度較薄,氣壓可能擊穿保氣層,土艙從而與外部空間形成通道,地表出現(xiàn)漏氣情況,產(chǎn)生較大變形,嚴(yán)重時可能會導(dǎo)致無法保壓,致使地表發(fā)生塌陷[18]。因而在預(yù)測氣壓輔助掘進(jìn)條件下盾構(gòu)掘進(jìn)引起的地表變形時需考慮上覆黏土層情況,而現(xiàn)有一般模型并未考慮該因素。2)氣壓輔助掘進(jìn)下地表變形更為復(fù)雜。由于土艙上部為氣壓,氣壓取值一般為土艙某一點位處靜水壓力值,因而掌子面上部總存在氣壓大于水土壓力的超壓區(qū)。田勇堅等[19]提到,氣壓輔助掘進(jìn)條件下,盾構(gòu)切口到達(dá)時地表就會產(chǎn)生隆起。另外,廣州地鐵18號線隴枕出入場線采用氣壓輔助工法施工區(qū)間段3個隧道軸線上方測點變形曲線如圖2所示,3個測點都在盾體通過時產(chǎn)生10 mm左右隆起變形,這說明帶壓氣體會充填盾體與土體之間的空隙,不僅在刀盤切口到達(dá)之前,而且在盾體通過時也會導(dǎo)致地表產(chǎn)生隆起,這與純土壓掘進(jìn)時的變形曲線不同[20]。
氣壓輔助掘進(jìn)條件下,黏土層厚度、氣壓大小與變形關(guān)系密切,之前預(yù)測模型并未考慮這些因素對于地表變形的影響,因而需要優(yōu)化之前模型的輸入?yún)?shù)以提高工程適用性。
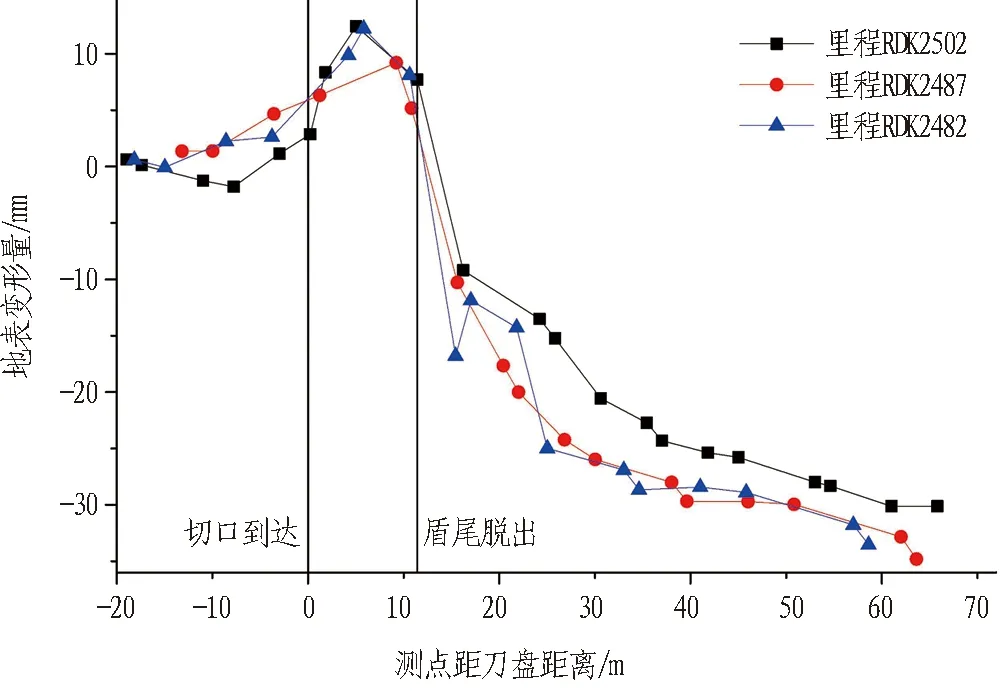
圖2 氣壓輔助掘進(jìn)條件下隧道軸線測點縱向變形曲線
2.2 模型輸入?yún)?shù)優(yōu)化
針對氣壓輔助掘進(jìn)工法特點,優(yōu)化PSO-SVM預(yù)測模型的輸入?yún)?shù)。
1)隧道幾何參數(shù)。隧道埋深與斷面直徑對地表變形影響較大,同一工程中斷面直徑為定值,因此選取隧道埋深H與斷面直徑D的比值H/D作為幾何因素輸入?yún)?shù)。
2)工程地質(zhì)參數(shù)。如2.1節(jié)所述,黏土層是氣壓輔助掘進(jìn)過程中的保氣層,其厚度對于地表變形量有很大影響,之前預(yù)測模型中并未考慮該參數(shù),因此在本文引入上覆黏土層厚度h這一參數(shù)作為預(yù)測模型的輸入?yún)?shù)。
考慮上覆非均質(zhì)土層物理力學(xué)性能會對地表變形產(chǎn)生較大影響,因此根據(jù)土層厚度對上覆土層標(biāo)貫次數(shù)加權(quán)平均值N′、上覆土層黏聚力加權(quán)平均值c′、上覆土層壓縮模量加權(quán)平均值E′ 3個參數(shù)進(jìn)行處理,詳細(xì)計算方法如下。
(6)
式中:n為土層種類總數(shù);hi為第i層土層厚度;h為上覆土總厚度。
3)盾構(gòu)施工參數(shù)。之前預(yù)測模型以土艙壓力作為輸入,并未考慮氣壓大小,而在氣壓輔助掘進(jìn)條件下,氣壓對于變形的影響不可忽視,因而在本文模型中增加土艙上部氣壓這個輸入?yún)?shù)。考慮到作用于掌子面前方及盾體上部土體的氣壓不僅在刀盤到達(dá)之前,而且在盾體通過地表測點時都會對測點變形量產(chǎn)生影響,因此取刀盤到達(dá)測點前至盾體通過測點時共10環(huán)氣壓平均值作為土艙上部氣壓Ap取值。
施工參數(shù)選取土艙上部氣壓Ap、同步注漿壓力Gp、同步注漿量Gv、總推力F作為輸入?yún)?shù)。
3 工程應(yīng)用
3.1 工程概況
廣州地鐵18號線隴枕出入場線RDK2+703~RDK1+809自RDK2+703里程處一次始發(fā),沿市南路自東向西前行364 m后接收,明挖186 m后自RDK2+153里程處盾構(gòu)二次始發(fā),繼續(xù)沿市南路掘進(jìn)。為合理控制地表變形,提高盾構(gòu)掘進(jìn)效率,廣州地鐵18號線隴枕出入場線自RDK2+522里程起采用氣壓輔助掘進(jìn)工法。
隧道采用土壓平衡盾構(gòu)施工,盾體長12.88 m,開挖直徑8.78 m,管片外徑8.5 m,內(nèi)徑7.7 m,環(huán)寬1.6 m。隧道上覆土層自上而下分別為雜填土、淤泥質(zhì)土、淤泥質(zhì)粉細(xì)砂、粉質(zhì)黏土、全風(fēng)化泥質(zhì)粉砂巖、強(qiáng)風(fēng)化泥質(zhì)粉砂巖、中風(fēng)化泥質(zhì)粉砂巖。詳細(xì)地質(zhì)剖面圖和地層主要物理力學(xué)參數(shù)分別如圖3和表1所示。
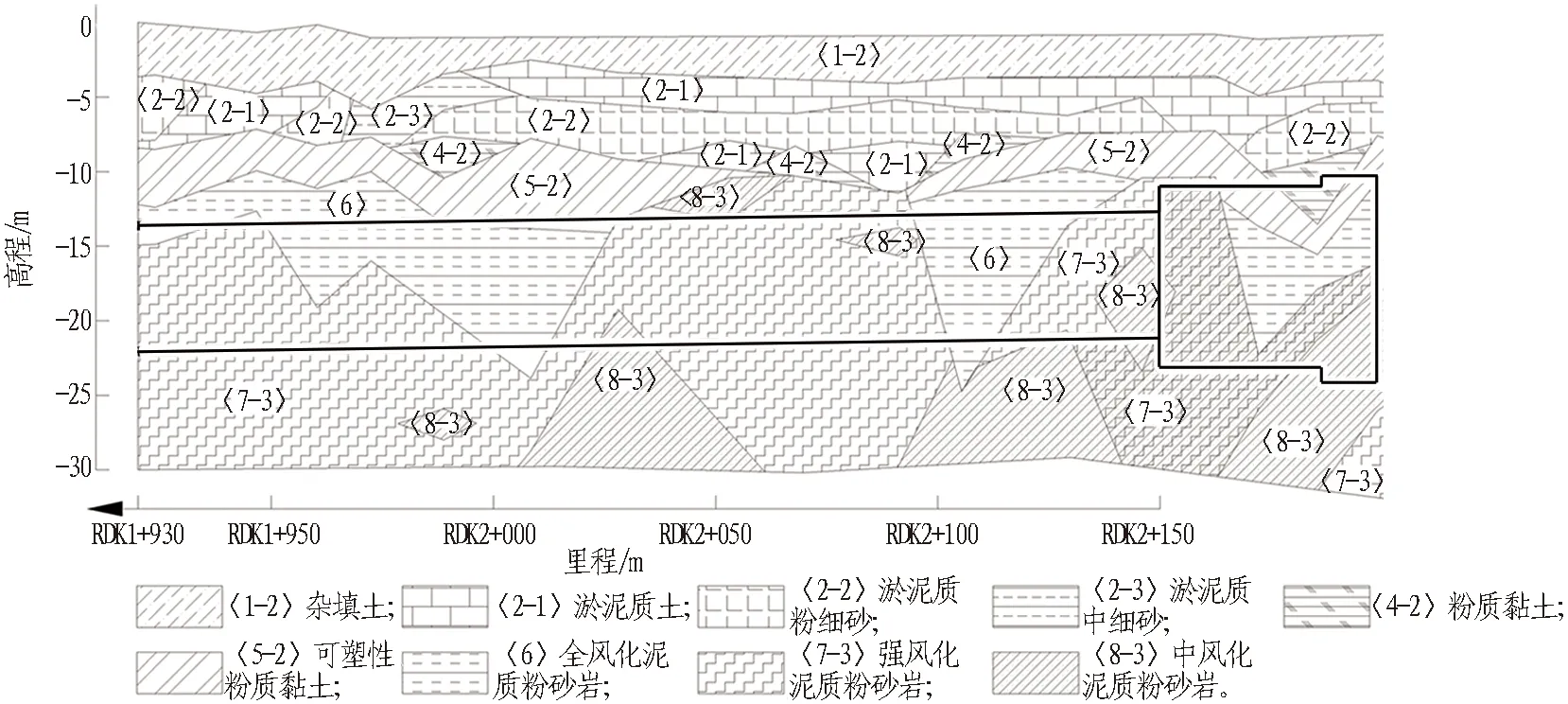
圖3 地質(zhì)剖面圖
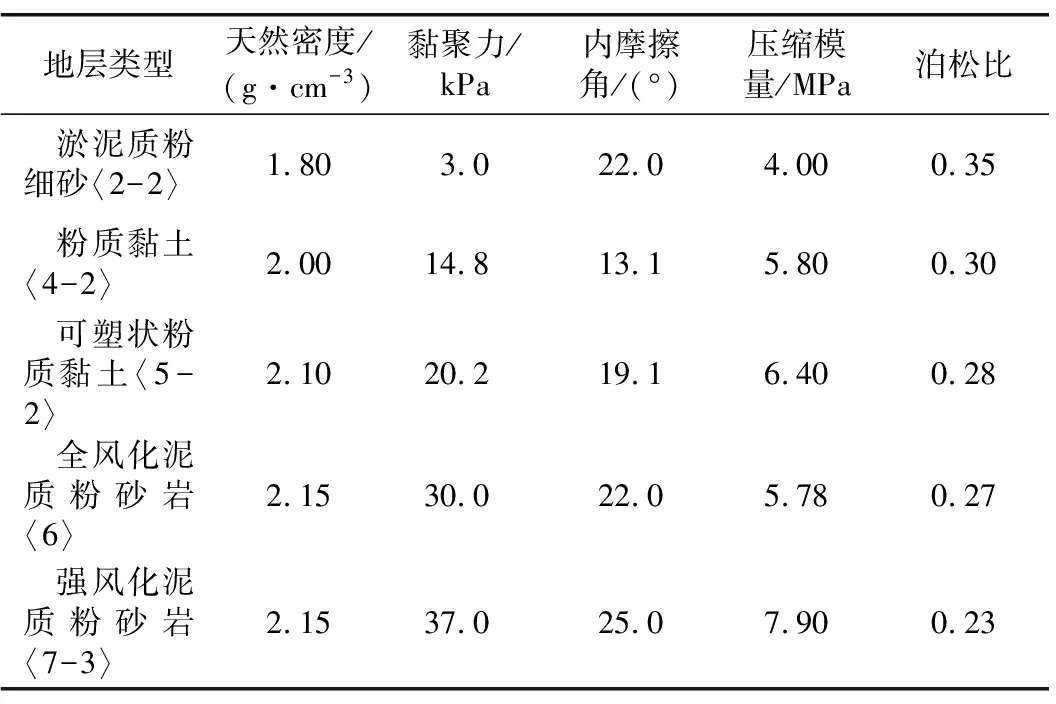
表1 地層主要物理力學(xué)性能參數(shù)
PSO-SVM預(yù)測模型數(shù)據(jù)為隴枕出入場線RDK2+522~RDK1+809段隧道軸線上方測點地表變形數(shù)據(jù),該段采用氣壓輔助掘進(jìn)工法,數(shù)據(jù)共計40組,其中,RDK2+522~RDK1+874段32組數(shù)據(jù)作為訓(xùn)練集構(gòu)建PSO-SVM預(yù)測模型,RDK1+859~+809共8組數(shù)據(jù)作為預(yù)測集。本工程中輸入?yún)?shù)上覆黏土層厚度h取為粉質(zhì)黏土〈4-2〉和可塑狀粉質(zhì)黏土〈5-2〉厚度之和。原始輸入?yún)?shù)分布范圍如表2所示。為消除輸入?yún)?shù)不同數(shù)量級對模型預(yù)測性能的影響,所有數(shù)據(jù)在訓(xùn)練預(yù)測前統(tǒng)一進(jìn)行歸一化處理。
(7)
式中:xmax為輸入?yún)?shù)最大值;xmin為輸入?yún)?shù)最小值。
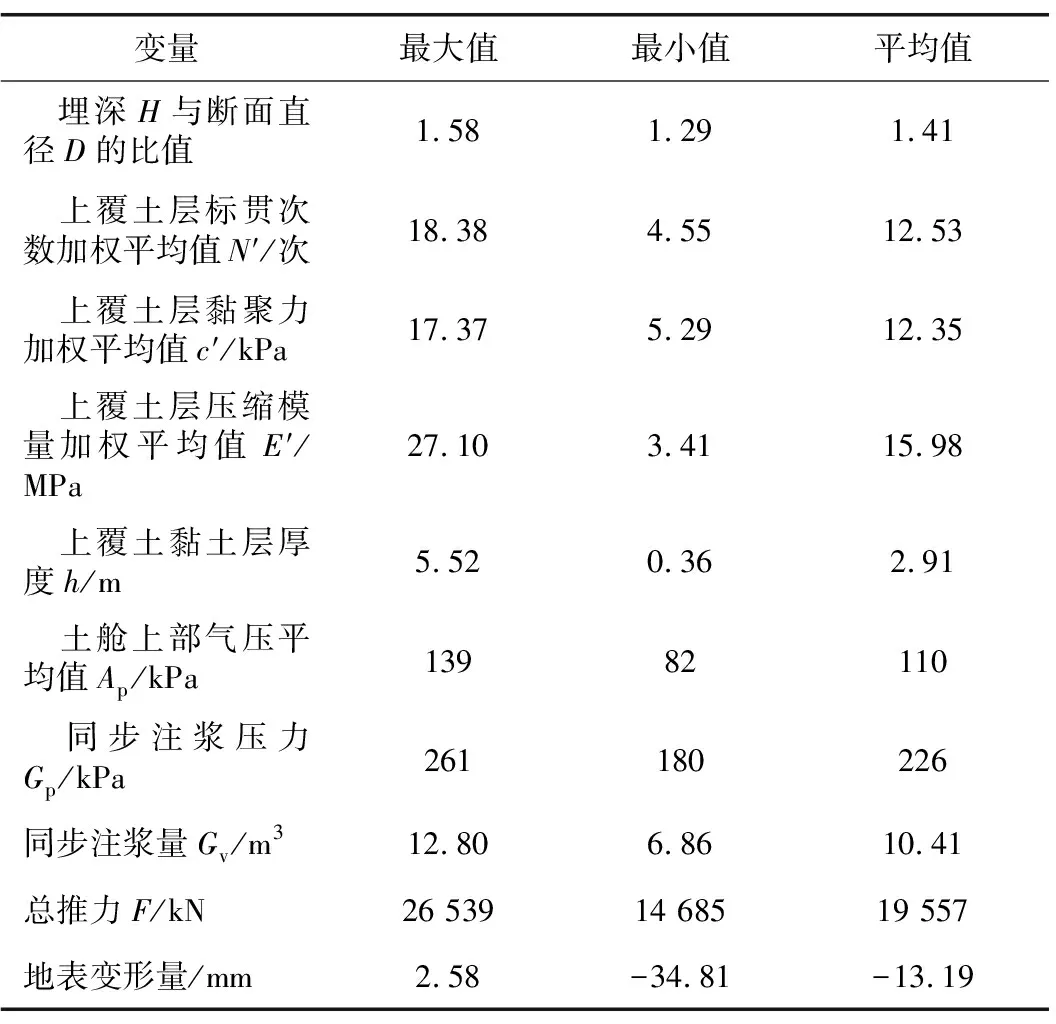
表2 輸入變量和輸出變量的分布范圍
3.2 超參數(shù)優(yōu)化結(jié)果
使用粒子群算法優(yōu)化支持向量機(jī)懲罰參數(shù)c和核函數(shù)參數(shù)g,2個超參數(shù)搜索區(qū)間均為0.001~10。經(jīng)多次試驗后,粒子群算法初始參數(shù)確定為: 粒子群規(guī)模為50,最大迭代次數(shù)為100,學(xué)習(xí)因子c1=c2=1.5,速度Vmax=-Vmin=0.5。為在前期進(jìn)行全局搜索,后期進(jìn)行局部搜索,慣性權(quán)重設(shè)置為線性遞減,表達(dá)式如式(8)所示。
(8)
式中:ωmax和ωmin分別為初始和最終慣性權(quán)重值,取值分別為0.9和0.4;i為當(dāng)前迭代次數(shù);T為最大迭代次數(shù),取值為100。
將廣州地鐵18號線隴枕出入場線RDK2+522~RDK1+809段隧道軸線上方測點地表變形數(shù)據(jù)前80%,即前32組,用于PSO-SVM模型的超參數(shù)確定。k折交叉驗證法中的k取為4,將32組數(shù)據(jù)分為4份,每份8組地表變形監(jiān)測數(shù)據(jù),每次3份訓(xùn)練、1份測試。
為分析該混合算法的可行性,對每一次迭代后的最小適應(yīng)度值進(jìn)行統(tǒng)計追蹤,結(jié)果如圖4所示。當(dāng)?shù)螖?shù)超過60次之后,適應(yīng)度值達(dá)到相對穩(wěn)定狀態(tài)。因此,本研究最終選取最小適應(yīng)度值對應(yīng)的懲罰參數(shù)c和核函數(shù)參數(shù)g值,即c=1.94,g=0.97。
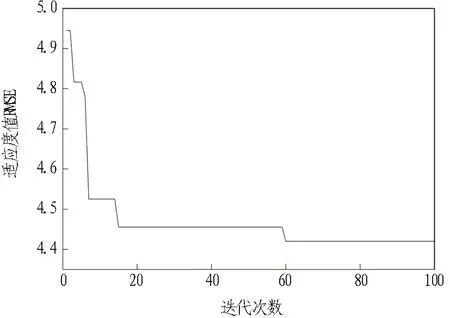
圖4 模型適應(yīng)度值進(jìn)化曲線
3.3 模型預(yù)測結(jié)果
為了驗證PSO-SVM預(yù)測模型的可靠性,取訓(xùn)練集數(shù)據(jù)(即前32組地表變形數(shù)據(jù))對PSO-SVM模型進(jìn)行訓(xùn)練,訓(xùn)練完成之后再次將訓(xùn)練集數(shù)據(jù)輸入到PSO-SVM模型中,評估訓(xùn)練效果。若訓(xùn)練效果符合要求,則將預(yù)測集數(shù)據(jù)(即后8組地表變形數(shù)據(jù))輸入到訓(xùn)練完成的模型中進(jìn)行預(yù)測。訓(xùn)練集、預(yù)測集的預(yù)測結(jié)果如圖5所示。
訓(xùn)練集中的隧道地表變形量分布范圍較廣,實測值與預(yù)測值的絕對誤差都較小,平均絕對誤差MAE=0.51 mm。該結(jié)果說明PSO-SVM模型較好地捕捉到前32組地表變形數(shù)據(jù)與影響因子間的內(nèi)在規(guī)律,以此為基礎(chǔ),將預(yù)測集(即后8組地表變形數(shù)據(jù))參數(shù)輸入到模型中,對前方開挖區(qū)間地表變形進(jìn)行預(yù)測分析,結(jié)果表明: 預(yù)測值和實測值的平均絕對誤差MAE=1.31 mm。
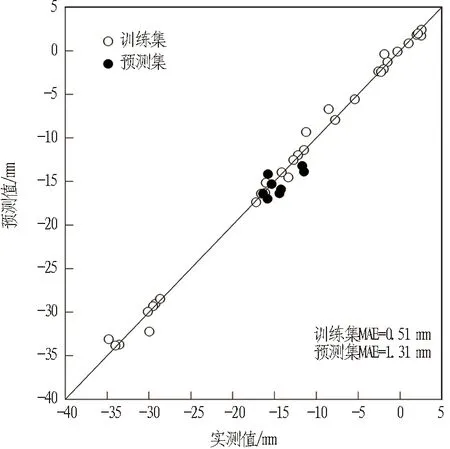
圖5 訓(xùn)練集與預(yù)測集分布圖
建立PSO-BP模型、SVM模型與PSO-SVM模型進(jìn)行對比分析,該3種模型均針對氣壓輔助掘進(jìn)工法優(yōu)化了輸入?yún)?shù)。對于模型超參數(shù),PSO-BP模型為粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu),最終確定1層隱含層和13個隱含層節(jié)點的結(jié)構(gòu); SVM模型參考Chen等[21]研究中的超參數(shù)取值,懲罰參數(shù)c=5.65和核函數(shù)參數(shù)g=0.06。各點預(yù)測結(jié)果如圖6所示。3種模型預(yù)測效果對比如表3所示。由表3可知,較之于PSO-BP模型和SVM模型,PSO-SVM模型具有更高的地表變形預(yù)測精度。雖然PSO-BP模型個別點預(yù)測誤差比PSO-SVM模型更小,但從預(yù)測值與實測值的均方根誤差來看,PSO-SVM模型僅為1.54,而PSO-BP模型和SVM模型分別為6.39和4.20,由此看出PSO-SVM模型表現(xiàn)出更好的預(yù)測穩(wěn)定性。
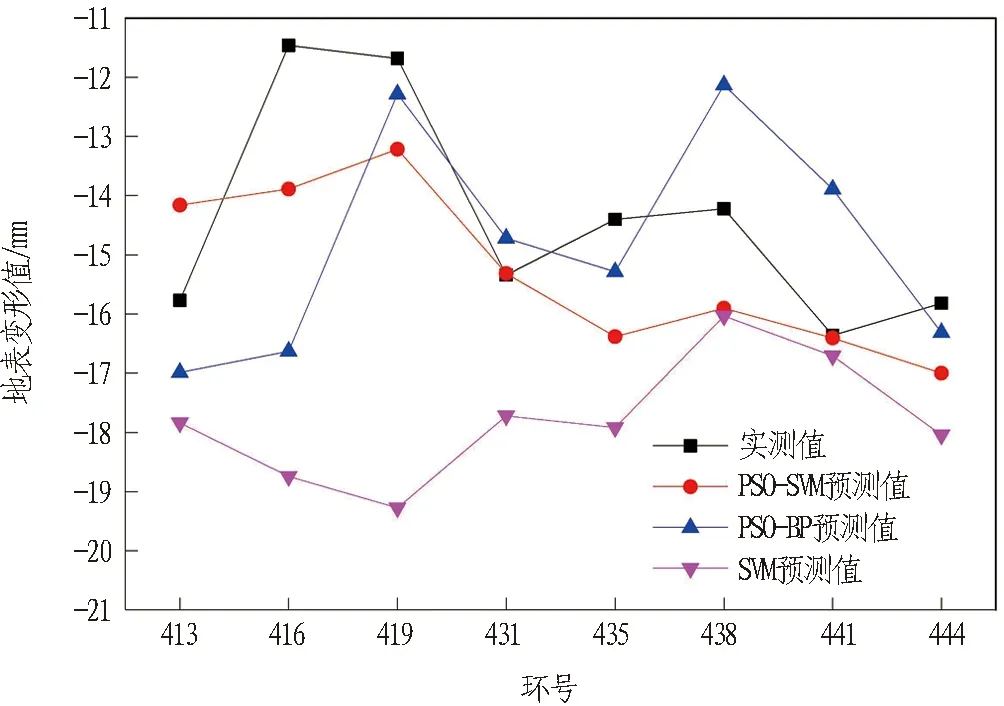
受地表環(huán)境影響,在419—431環(huán)未設(shè)置監(jiān)測點。
圖6 PSO-SVM、PSO-BP、SVM模型預(yù)測值與實測值比較
Fig. 6 Comparison of measured values and values predicted by PSO-SVM, PSO-BP, and SVM models

表3 3種模型預(yù)測結(jié)果對比
4 結(jié)論與討論
1)本文引入支持向量機(jī)(SVM)理論,利用粒子群算法(PSO)對支持向量機(jī)的超參數(shù)組合進(jìn)行優(yōu)化,以交叉驗證集的均方根誤差平均值作為粒子群算法的適應(yīng)度函數(shù),獲得了支持向量機(jī)最佳超參數(shù)組合,提升了模型的預(yù)測精度。
2)根據(jù)氣壓輔助掘進(jìn)下地表變形特征,合理引入上覆黏土層厚度和土艙上部氣壓表征土層氣密性和氣艙壓力對隧道地表變形的影響,針對上覆非均質(zhì)土層改進(jìn)模型參數(shù)計算方法,對PSO-SVM模型輸入?yún)?shù)進(jìn)行優(yōu)化,使用該模型對廣州地鐵18號線隴枕出入場線某使用氣壓輔助掘進(jìn)工法的盾構(gòu)區(qū)間進(jìn)行預(yù)測,結(jié)果表明該模型預(yù)測平均絕對誤差為1.31 mm,可以較好滿足工程實際需要。
3)基于平均絕對誤差、最大絕對誤差和均方根誤差的對比分析,優(yōu)化超參數(shù)后的PSO-SVM模型預(yù)測效果精度和穩(wěn)定性整體優(yōu)于PSO-BP模型和傳統(tǒng)SVM模型,PSO-SVM模型表現(xiàn)出更為優(yōu)越的工程適用性。
本研究優(yōu)化了PSO-SVM模型的輸入?yún)?shù),雖在一定程度上考慮了氣壓輔助掘進(jìn)工法對變形的影響,但氣壓影響與地層條件關(guān)聯(lián)密切,對于地質(zhì)參數(shù)的輸入仍需進(jìn)一步精細(xì)化研究。此外,本文模型對于該工程地表變形具有一定的預(yù)測精度,但數(shù)據(jù)樣本來自同一工程,由于現(xiàn)場工況的復(fù)雜性,應(yīng)盡量收集其他類似工程下實測數(shù)據(jù),進(jìn)一步提高該模型的適用性。同時,下一步可開發(fā)適用于該工法的動態(tài)與實時地表變形預(yù)測模型,以便更好地指導(dǎo)工程施工。

