考慮碰撞效應的鐵路連續梁橋MTC減震體系地震響應研究
許鑫祥 陳士通 張茂江 李然
1.石家莊鐵道大學河北省交通應急保障工程技術研究中心,石家莊050043;2.石家莊鐵道大學國防交通研究所,石家莊050043;3.石家莊鐵道大學土木工程學院,石家莊050043
地震時鐵路連續梁橋破壞現象普遍發生,主要原因是連續梁橋的一聯只設置一個固定墩來滿足溫度荷載引起的變形需求,地震作用下上部結構產生的縱向荷載全部由固定墩承擔,常導致固定墩發生彎剪破壞、伸縮縫破壞、落梁等震害[1]。研發鎖定裝置以提高橋梁抗震性能已成為當前的發展趨勢。文獻[2]分析了速度激活的Lock-up裝置在鋼桁梁橋中應用時的減震性能。文獻[3]提出了加速度激活的慣性力激活(Inertial Force Activation,IFA)減震裝置,并對減震效果進行了深入探究。文獻[4]提出了一種安全帶減震裝置,采用振動臺試驗對減震機理進行了探究。文獻[5]提出了一種加速度激活的鎖死銷裝置,并對參數進行了優化。
上述鎖定裝置在地震發生時只能介入一種限位剛度,無法適應復雜多變的地震狀態。若限位剛度設置不當,不僅達不到耗能減震的效果,甚至可能增大連續梁橋的地震響應。因此,文獻[6]提出一種位移激活的分階段適時連接鎖定控制(Multi-stage Timely Connection Control,MTC)裝置。MTC裝置構造簡單,選用材料的可靠性高,能夠保持長期穩定,在活動墩上安裝MTC裝置可提高連續梁橋抗震性能。既有研究均以某一聯連續梁橋為分析對象,并未考慮相鄰梁體間的碰撞效應。鐵路連續梁橋在大震作用下發生相鄰梁體碰撞的可能性較大,且碰撞效應是影響橋梁地震響應及裝置抗震性能的一個重要因素[7-8]。
本文以一座鐵路連續梁橋為例,分析考慮碰撞效應時連續梁橋MTC減震體系的地震響應,為MTC裝置在鐵路連續梁橋上的應用提供技術支撐。
1 MTC裝置及力學模型
MTC裝置(圖1)是一種安裝在活動墩與梁體之間減震裝置,利用墩梁相對位移予以激活,由限位裝置(軟鋼擋板、金屬橡膠和彈簧)、水平連桿、鎖緊螺母和連接牛腿組成。限位裝置與活動墩相連,分為Ⅰ區和Ⅱ區限位裝置。水平連桿穿過限位裝置的空心區域,兩端與固定在梁體上的牛腿鉸接。鎖緊螺母與Ⅰ區、Ⅱ區限位裝置之間分別預留激活間隙Δ1和Δ2,且Δ1<Δ2。

圖1 MTC裝置構造
發生地震且達到激活條件后,限位裝置與鎖緊螺母接觸,活動墩與梁體通過限位裝置中的軟鋼擋板等彈性連接,二者相對運動受到限制,活動墩則參與抵抗水平地震力并實現耗能減震。連續梁橋正常運營狀態下,最大墩梁相對位移小于Δ1,裝置不激活;中小震作用下墩梁相對位移大于Δ1且小于Δ2,Ⅰ區限位裝置激活;大震作用下墩梁相對位移大于Δ2,Ⅱ區限位裝置激活,此時Ⅰ區、Ⅱ區限位裝置共同抵抗水平地震力。該裝置可根據地震力大小實現分級減震,克服了既有鎖定裝置無法適應復雜多變的地震狀況的不足,同時可通過軟鋼擋板等實現耗能減震。根據裝置應用的場地條件和橋梁結構參數,設置主要參數(激活間隙、限位剛度)并選擇合理的布設方案,即可達到較好的減震效果。
MTC裝置力學模型見圖2。其中,fsm、cm(m=1、2分別代表Ⅰ區、Ⅱ區限位裝置)分別為Ⅰ區和Ⅱ區限位裝置的軟鋼擋板屈服力、阻尼;kmn為限位剛度(n=1、2、3),km1、km2、km3分別為限位裝置中的彈簧剛度、軟鋼擋板剛度、金屬橡膠剛度。鑒于軟鋼擋板屈服后仍可發揮一定的限位作用,為便于理解及模型中參數設置,以km,q和km,h分 別 表示限 位裝置 屈 服前后 的總剛度。

圖2 MTC裝置力學模型
根據裝置工作原理得到MTC裝置的力-位移曲線,見圖3。其中,F1和F2分別為Ⅰ區、Ⅱ區軟鋼擋板承受的力。
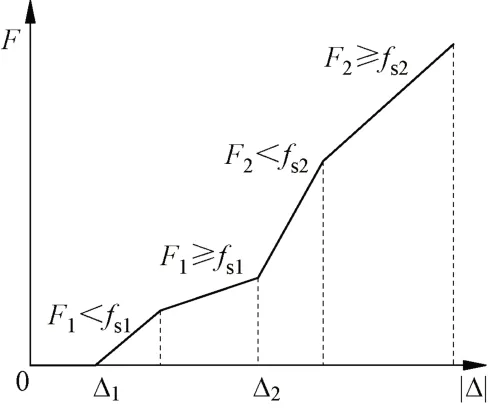
圖3 MTC裝置力-位移曲線
2 工程概況及分析模型
以一座鐵路橋梁(圖4)為分析對象,連續梁梁體采用單箱單室變高度直腹板箱形截面,主墩墩頂梁高9.60 m,跨中及連續梁邊墩墩頂梁高5.80 m,梁高按1.8次拋物線變化,箱梁頂寬13.40 m,底寬6.70 m;兩側32 m梁體采用單箱雙室斜腹板等高箱梁,梁高3.10 m,頂寬12.79 m,底寬6.85 m,梁體混凝土彈性模量為3.45×107kN∕m2。采用實體型圓端橋墩,截面面積30.34 m2,縱向抗彎慣性矩33.10 m4,墩身混凝土彈性模量為3.0×107kN∕m2。H1—H7依次為1#—7#橋墩的高度,均設為20 m。
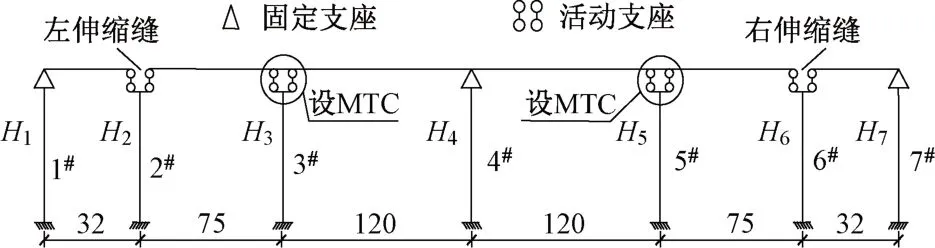
圖4 橋跨布置(單位:m)
采用ANSYS建立全橋有限元模型進行地震反應分析。墩梁均采用梁單元模擬;固定支座及活動支座采用耦合命令模擬;MTC裝置采用combin40和link1單元組合模擬,通過生死單元法控制裝置激活。橋墩與地面按固接處理,墩梁處于彈性范圍。模型中MTC裝置主要參數取值:限位裝置剛度k1,q=4.22×105kN∕m、k1,h=2.11×104kN∕m、k2,q=1.69×106kN∕m、k2,h=8.45×104kN∕m;激活間隙Δ1=0.010 m、Δ2=0.012 m。
采用接觸單元法中的Kelvin模型模擬碰撞效應,通過在伸縮縫處設置combin40單元實現。伸縮縫處的力-位移關系為
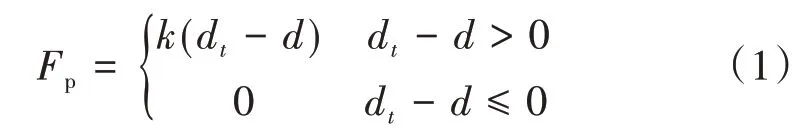
式中:Fp為碰撞力;k為伸縮縫處接觸剛度,取發生碰撞的兩梁體軸向剛度的較大值[9];d為伸縮縫寬度;dt為地震作用下t時刻相鄰梁體間的相對位移。
Kelvin碰撞模型如圖5所示。其中,阻尼c為碰撞過程中的能量損耗。
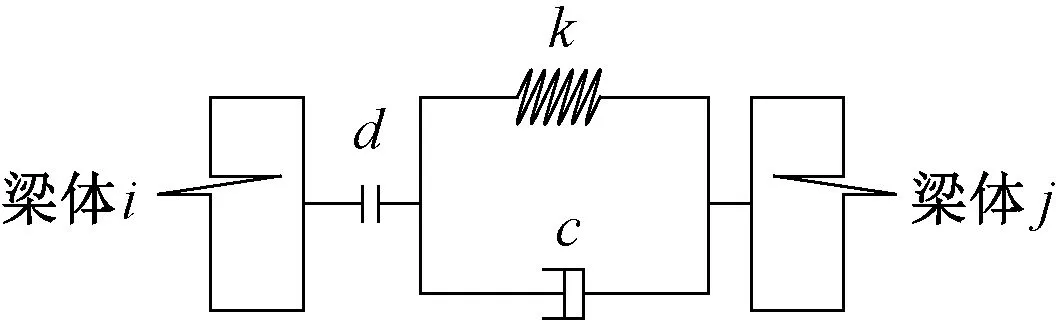
阻尼c的計算公式為
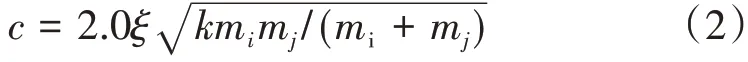
式中:mi、mj分別為伸縮縫兩側梁體i、j的質量;ξ為阻尼比。
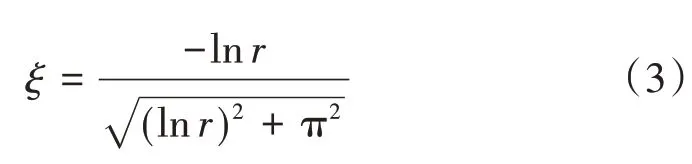
ξ的計算公式為式中:r為恢復系數,完全彈性碰撞時r=1,完全塑性碰撞時r=0,混凝土材料對應的Kelvin模型中碰撞恢復系數取0.65[10],可模擬混凝土結構在碰撞過程中的能量損失。
根據式(2)、式(3)及橋梁結構參數,得到ξ=0.135 8,c=8.18×104kN·s∕m,k=1.36×107kN∕m。
為便于分析碰撞效應對鐵路連續梁橋MTC減震體系受力的影響情況,設計4種工況分析減震效果,見表1。其中,不考慮碰撞效應的工況認為相鄰梁體間獨立運動,未在伸縮縫處設置碰撞單元;考慮碰撞效應的工況即在伸縮縫處設置碰撞單元,在3#、5#活動墩上布置MTC裝置(參見圖4)。

表1 分析工況
采用減震率λ0、λp分別表示考慮碰撞效應前后MTC裝置的減震效果,其計算式分別為
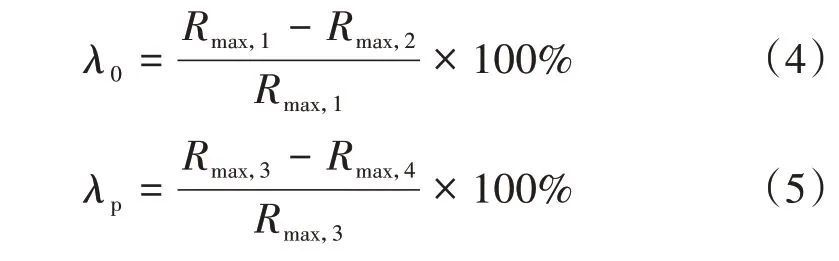
式中:Rmax,1—Rmax,4分別為工況1—工況4中連續梁梁體最大位移或固定墩(4#墩)最大地震響應。
選取3條地震波(表2)順橋向輸入,地震波峰值加速度均調至0.3g。
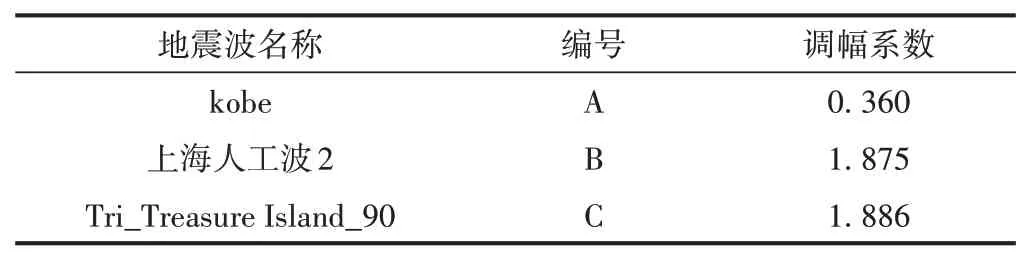
表2 輸入地震波參數
3 碰撞效應對連續梁橋MTC減震體系的影響
3.1 碰撞效應對減震效果的影響
3條地震波激勵下,考慮碰撞效應前后的連續梁梁端位移及固定墩減震效果對比見表3。可知:

表3 梁端位移及固定墩減震效果對比
1)考慮碰撞效應后,梁端位移及固定墩剪力、彎矩減震率均有所下降,其中B波激勵下減震率降幅最大,A波激勵下減震率降幅最小。說明碰撞效應對MTC裝置減震效果有一定的降低作用,降低程度與地震波特性相關,MTC裝置減震分析時不宜忽略碰撞效應的影響。
2)即使考慮碰撞效應,各地震波輸入下的減震率也均在20%以上,說明MTC裝置在相鄰梁體發生碰撞時可有效提高鐵路連續梁橋抗震性能。
為進一步探究碰撞效應對MTC裝置減震效果的影響,繪制B波輸入下時程曲線,見圖6。其中,圖6(d)為考慮碰撞效應時連續梁橋左、右兩伸縮縫處碰撞力時程曲線,正值表示左伸縮縫處碰撞力,負值表示右伸縮縫處碰撞力。

圖6 B波輸入下時程曲線
由圖6可知:
1)未安裝MTC裝置時,在首次碰撞(8.48 s)前,工況3梁端位移及固定墩地震響應時程曲線與工況1時程曲線重合,8.48 s后發生多次碰撞,工況1和工況3時程曲線逐漸分離,且工況1的梁端位移及固定墩墩底剪力、彎矩極值均大于工況3。原因在于工況3中相鄰梁體間的碰撞限制了連續梁橋的梁體運動并耗散了部分地震能量,從而減小了梁端位移及固定墩地震響應,但也增加了伸縮縫和梁體發生破壞的風險。
2)安裝MTC裝置后,工況2與工況4的梁端位移及固定墩剪力、彎矩時程曲線基本重合。原因是工況4中雖然考慮了碰撞效應,但MTC裝置的激活使碰撞次數減少至1次,且碰撞力極值大幅降低(僅為工況3中碰撞力極值的21.58%),說明梁體間碰撞對安裝MTC裝置的連續梁橋梁體位移及固定墩地震響應影響極小。連續梁橋安裝MTC裝置后,是否考慮碰撞效應對其梁端位移及固定墩地震響應影響有限;但未安裝MTC裝置時,考慮碰撞效應后連續梁橋梁端位移及固定墩地震響應明顯減小。可見MTC裝置不僅有效降低了連續梁橋梁端位移及固定墩地震響應,而且減小了碰撞力及碰撞次數,可起到保護伸縮縫及梁體的作用。
3.2 碰撞效應對活動墩地震響應的影響
MTC裝置減震核心思想是利用活動墩的抗震潛能,提高橋梁整體抗震性能。因此保護活動墩震中安全是裝置成功應用的前提,有必要探究碰撞效應對活動墩受力的影響情況。3條地震波激勵下活動墩地震響應見圖7。

圖7 活動墩地震響應
由圖7可知:①同一地震波激勵下,工況1與工況3的活動墩墩底剪力、彎矩極值差別很小,工況2與工況4的活動墩墩底剪力、彎矩極值相差不大,說明無論是否安裝MTC裝置,碰撞效應對活動墩受力影響極小。②安裝MTC裝置的活動墩地震響應比未安裝時明顯增加,可采取調整MTC裝置限位剛度的措施,在不過多增大活動墩地震響應的同時提高減震效果。
為進一步探究碰撞效應對活動墩地震響應的影響,給出3條地震波激勵下工況3和工況4中左、右伸縮縫碰撞力最大值及碰撞次數(兩伸縮縫碰撞次數之和),見表4。以B波激勵下5#活動墩為例,繪制墩底彎矩時程曲線,見圖8。

表4 伸縮縫處地震響應

圖8 B波激勵下5#活動墩墩底彎矩時程曲線
由表4和圖8可知:
1)未安裝MTC裝置時,首次碰撞前,工況3與工況1的墩底彎矩時程曲線完全重合;發生碰撞后,二者時程曲線雖然不再重合,但走勢與極值仍相差不大。原因是雖然梁體間發生碰撞,但未安裝MTC裝置時活動墩與梁體可縱向自由滑動,因此碰撞力大部分傳遞到了固定墩上,對活動墩受力狀態影響有限。
2)安裝MTC裝置后,無論是否發生碰撞,工況2與工況4的時程曲線均幾乎完全重合,此現象與未安裝MTC裝置時有較大區別。結合表4中安裝MTC裝置前后梁端碰撞力和碰撞次數可知,激活MTC裝置大大減小了梁體間碰撞力及碰撞次數,且3#、5#活動墩處均安裝了MTC裝置,可與固定墩共同承擔碰撞力,因此碰撞效應對單個活動墩地震響應的影響極小。
4 結論
1)考慮碰撞效應后,MTC裝置的減震效果比未考慮碰撞時有所下降,但仍可有效降低鐵路連續梁橋梁端位移及固定墩剪力、彎矩。
2)碰撞效應在伸縮縫處產生碰撞力,但MTC裝置可有效降低梁體間碰撞力并減少碰撞次數,對伸縮縫起到保護作用。
3)連續梁橋應用MTC裝置減震時,是否考慮碰撞效應對活動墩地震響應影響極小。
為驗證MTC裝置減震的有效性,振動臺模型試驗將是下一步研究工作的重點。

