跨座式單軌交通軌道不平順對梁軌振動響應的影響

張凱 朱爾玉 劉旭鍇 周燕

1.天津大學建筑工程學院，天津300072；2.天津市賽英工程技術咨詢有限公司，天津300051；3.北京交通大學土木建筑工程學院，北京100044；4.天津市政工程設計研究總院有限公司，天津300051；5.天津城建大學天津市土木建筑結構防護與加固重點實驗室，天津300384

跨座式單軌交通是一種新型軌道交通制式，載客量適中，占地少，造價低，適應地形能力強［1］，近幾年在我國得到了蓬勃發展。

軌道不平順是引起機車車輛振動的重要因素。單軌交通在全世界范圍內應用規模較小，因此關于單軌交通不平順功率譜及軌道不平順對單軌交通車橋耦合振動性能影響的研究較少。2000年，日本的Goda等［2］采用多體動力學方法建立了單軌車輛的動力學方程，對車輛通過小半徑曲線橋時車橋耦合動力學性能進行了仿真研究。2005年，日本的Lee等［3］建立車橋系統三維有限元模型，開發了相應的動力計算程序，研究了旅客數量變化對乘坐舒適性的影響。2006年，Lee等［4］對大阪一座跨徑44 m鋼桁架橋的車輛-鋼橋耦合動力作用進行了分析計算，并根據鋼軌道梁橋表面軌道不平順實測結果，用Monte Carlo法進行了數值模擬。在國內，任利惠、沈鋼等［5-6］較早對單軌機車車輛進行了動力學研究，考慮單軌輪胎的徑向剛度和側偏效應、縱向滑轉，采用線性化輪胎模型建立單軌車輛動力學方程，編寫了單軌車輛動力學圖形化仿真程序，研究了單軌車輛轉向架運動穩定性，但其研究模型未考慮車橋耦合振動的影響，未建立橋梁模型。此后，劉羽宇、李小珍、趙樹恩等［7-9］考慮車橋耦合的影響，分析了單軌交通簡支軌道梁的車橋耦合振動性能。郭文華等［10］研究了單軌交通車輛通過連續梁橋的車橋耦合振動性能，為單軌交通軌道連續梁設計提供理論支撐。高玉峰、施洲等［11-12］通過試驗檢測，評價了重慶單軌交通系統的乘坐舒適性和橋梁安全性。

由于實測數據不足，既有研究一般不把軌道不平順的研究作為分析重點。本文結合我國預制混凝土（Precast Concrete，PC）軌道梁的制作工藝和施工控制精度水平，對單軌PC軌道梁軌道不平順功率譜進行分析，并采用三角級數法模擬生成軌道不平順時程曲線，將其作為外激勵輸入15個自由度的單軌交通車橋耦合振動模型；應用非線性振動數值算法，編制單軌交通車橋耦合振動分析軟件，研究軌道不平順和車速對單軌交通車橋耦合振動響應的影響。

1 單軌交通軌道不平順功率譜

1.1 功率譜函數

單軌交通軌道梁既是機車車輛的承力主梁，同時也是車輛的運行軌道，因此單軌交通的軌道不平順即為軌道梁的表面不平順。PC軌道梁采用工廠化預制，整體吊裝，施工精度高，精度控制嚴格。PC軌道梁側面精度受預制大鋼模板控制，由于鋼模板加工制作精度較高，PC軌道梁的側面不平順接近鋼軌道梁。但是，PC軌道梁頂面制作精度稍差，一般認為其頂面不平順高于鋼軌道梁頂面不平順，并低于普通鐵路的軌道不平順。

目前國內外尚缺少單軌交通軌道不平順的功率譜規范標準，也缺少相應的大規模實測資料。只有文獻［4］結合一跨鋼桁架橋的實測數據模擬給出了鋼軌道梁的軌道不平順功率譜密度函數，即

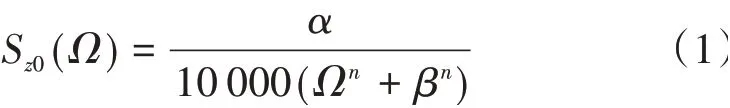
式中：Sz0(Ω)為采用Monte Carlo法模擬的軌道不平順功率譜密度函數，m2∕（m-1）；Ω為采樣的空間頻率，m-1；α、n、β為相關參數。

跨座式單軌各車輪的相關參數取值見表1。

表1 各車輪軌道不平順功率譜相關參數

準確的PC軌道梁表面軌道不平順須通過實測得到，而目前國內外尚缺乏PC軌道梁軌道不平順的實測數據。因而，本文的后續分析中，PC軌道梁導向輪和穩定輪軌道不平順功率譜密度函數采用文獻［4］中鋼軌道梁的功率譜函數，走行輪軌道不平順功率譜密度函數采用文獻［4］鋼軌道梁功率譜和美國6級軌道高低不平順功率譜進行對比分析。

1.2 數值模擬

軌道不平順的數值模擬方法很多，其中三角級數法較簡單［13］。三角級數法假定軌道不平順是具有0均值的各態歷經平穩隨機過程，將平穩高斯過程的復數傅里葉級數轉化為三角級數疊加生成時程樣本。

根據三角級數法疊加原理，基于美國6級鐵路及鋼軌道梁功率譜［4］得出軌道不平順時程曲線，如圖1所示。

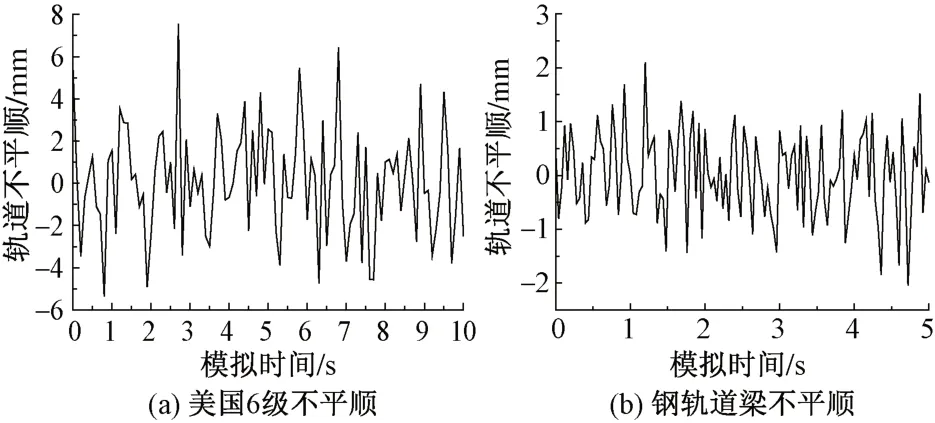
圖1 采用不同功率譜函數模擬的軌道不平順時程曲線

2 單軌交通車橋耦合振動分析模型

2.1 車輛和軌道梁動力模型

單軌交通軌道梁承重和運行軌道合二為一，其車橋耦合振動系統通過車輛-軌道梁來建立。單軌交通系統車輛轉向架為剛性轉向架，車軸不能相對轉向架搖頭，同一車軸上的左右輪胎不能相對轉動；其導向輪、走形輪、穩定輪為橡膠輪胎，充當一系懸掛，如圖2所示。單軌交通車輛運行過程中，充氣輪胎與軌道梁密切接觸，橡膠輪胎具有六分力的力學特性，其六分力作用通過線彈簧系數表達［9，13］。

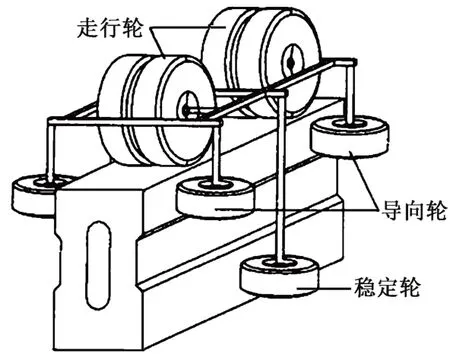
圖2 單軌交通系統車輛轉向架示意

單節車輛由車體和前后2個轉向架組成，共3個剛體；每個剛體可簡化考慮5個自由度（沉浮、橫移、點頭、搖頭、側滾），共15個自由度［7-10，13］。建立車輛動力分析模型，如圖3所示。建模時考慮一系輪胎懸掛系統走行輪、導向輪和穩定輪徑向剛度、徑向阻尼，走形輪胎側偏剛度、回正剛度；二系空氣彈簧垂向、橫向的剛度、阻尼。相關參數取值參考文獻［13］。

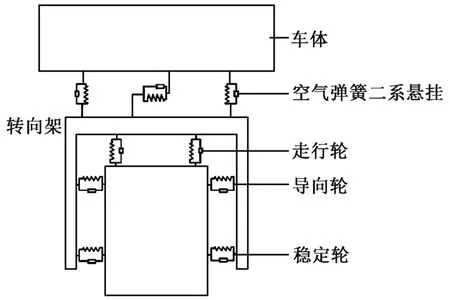
圖3 單軌交通車輛簡化分析模型

軌道梁動力模型采用空間梁單元模型，每個節點具有6個自由度，即3個線位移和3個角位移。

2.2 車橋耦合作用

單軌交通系統以輪軌接觸面為界分為車輛系統和橋梁系統，通過輪胎的變形分別對車輛和橋梁施加一組大小相等、方向相反的車橋耦合作用。輪胎的變形為輪胎中心與輪軌接觸面的位移差。基于單軌車輛剛性轉向架原理，利用幾何關系，由機車車輛轉向架的振動位移可以推導出輪胎中心的振動位移。輪軌接觸面的位移包括兩部分：輪軌接觸面的軌道不平順；軌道梁中心節點振動引起的輪軌接觸面位移，相當于附加軌道梁輪軌接觸面不平順［14］。

輪軌接觸面位移的表達式為

式中：Ucb為輪軌接觸面動位移矩陣；N為軌道梁離散單元節點與輪軌接觸面動位移的轉換關系矩陣；Ubc為軌道梁離散單元節點的動位移矩陣；R為輪軌接觸面的軌道梁表面不平順幅值矩陣。

通過輪胎變形可得到耦合作用荷載，據此建立單軌交通車橋耦合振動方程，即

式中：Mvv、Mbb分別為車輛、軌道梁質量矩陣分別為車輛、軌道梁的振動加速度矩陣；Cvv、Cvb、Cbv、Cbb分別為車輛、車輛和單軌耦合作用部分、單軌和車輛耦合作用部分、軌道梁的阻尼矩陣分別為車輛、軌道梁的振動速度矩陣；Kvv、Kvb、Kbv、Kbb分別為車輛、車輛和單軌耦合作用部分、單軌和車輛耦合作用部分、軌道梁的剛度矩陣；Xv、Xb分別為車輛、軌道梁離散節點動位移矩陣；Fv、Fb分別為施加在車輛上的輪軌作用矩陣、施加在單軌軌道梁上的輪軌作用矩陣。

振動方程中軌道梁和車輛質量、剛度、阻尼可根據相應模型推導得到，輪軌作用根據線性化輪胎模型的變形-荷載關系得到。

3 求解車橋振動方程

根據式（3），輪軌作用力Fv、Fb與車輛、軌道梁兩個子系統都有關系，因此求解時須在每個時間步迭代求解，在每個時間步內兩個子系統的動力響應均滿足收斂條件時才能進行下一個時間步內的迭代。求解流程見圖4。t1、t2分別表示方程初始時間和后續時間步求解時間，Δt表示時間步長。

對于圖4的求解流程，有以下幾點說明：

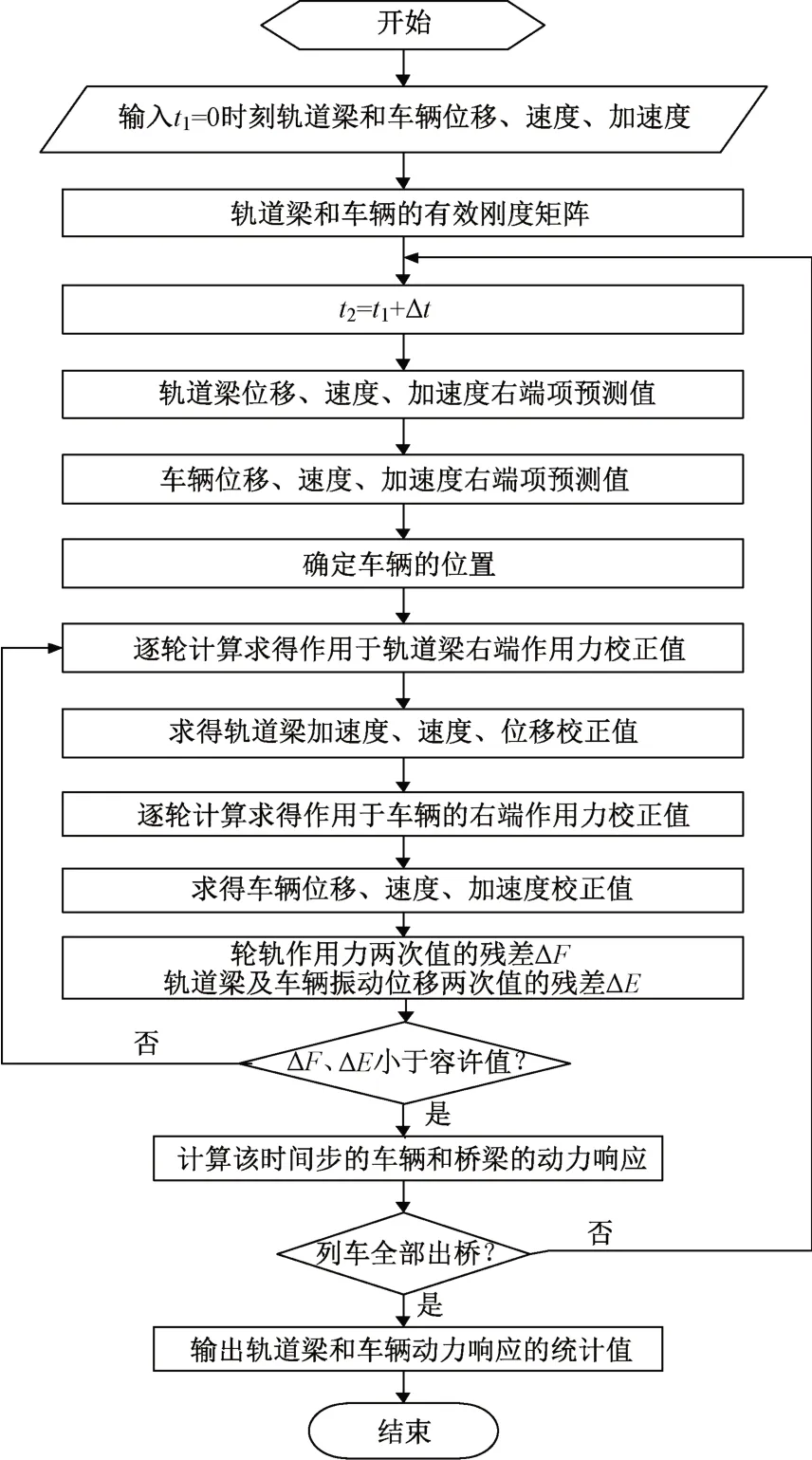
圖4 跨座式單軌交通車橋系統動力求解流程

1）每個時間步內，車輛和軌道梁子系統動力響應均采用Newmark-β迭代法求解。

2）采用預測-校正的方法進行迭代分析。取t1時刻的振動位移作為t1+Δt時刻的振動位移預測值，利用增量方程求得位移增量，與位移預測值相加得到位移校正值，以此作為預測值再次迭代。

3）每一時間步內，兩個子系統兩次校正值均滿足收斂條件才可進行下一步的迭代。迭代收斂標準為

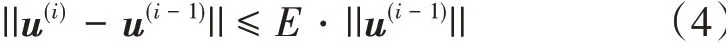
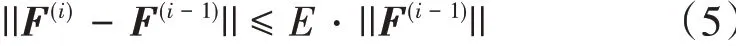
式中：E為給定的相對誤差，通常可取0.01%；u為位移矩陣；F為作用力矩陣；上標i、i-1表示時間步內相鄰的兩次迭代，其中時間步長Δt取0.000 1 s。

4 單軌車橋耦合振動的影響因素

以重慶市一單軌交通曲線梁橋為實例，基于上述方法，采用Compaq Visual Fortran 6.5平臺編制車橋耦合振動分析軟件，討論軌道不平順、車速對單軌交通車橋耦合振動的影響。

4.1 現場測試試驗

選取重慶市跨座式單軌Ⅱ號線路一期工程進行現場測試試驗。以其中某橋跨作為測試橋跨。該跨橋為預應力鋼筋混凝土曲線梁橋，跨徑18.927 m，曲線半徑147.95 m；主梁為0.85 m寬標準預應力混凝土PC軌道梁；橋梁下部結構為2 m×2 m方形墩，墩高11.18、11.89 m。基礎采用鉆孔灌注樁基礎。

試驗內容包括自振特性試驗以及靜停、行車、制動狀態下的動載試驗、乘坐舒適性試驗。試驗時，單軌列車以10～65 km∕h通過測試橋跨，并輔以制動工況，測試軌道交通系統上部結構的動力響應，同時進行全線車輛行駛過程中的乘坐舒適性試驗。

在1∕6、1∕3、1∕2、2∕3、5∕6梁跨截面處布設測振傳感器，測試梁體的各階振型及頻率。在軌道梁和機車車輛上布置位移和加速度傳感器，測試橋梁縱橫向動位移及加速度、車輛轉向架和車體振動加速度。在車體的車門附近座椅邊、轉向架中心線上布置三向加速度傳感器，測試旅客乘坐舒適性。

4.2 計算參數取值及分析工況

重慶單軌機車車輛動力學參數沒有實測數據，考慮到該單軌車輛為日本引進，計算時車輛參數根據文獻［4］中運營線路車輛參數取值。

為了分析軌道不平順的影響，按照推測的軌道不平順可能的分布范圍，定義四種不平順工況。

工況1：PC軌道梁表面完全光滑，不考慮軌道不平順激勵。

工況2：PC軌道梁制作精度與鋼軌道梁相同，軌道不平順均按照文獻［4］中的鋼軌道梁取值。

工況3：PC軌道梁頂面不平順采用美國6級鐵路不平順，側面按照文獻［6］中的鋼軌道梁取值。

工況4：實測結果。

4.3 梁體自振特性

梁體自振特性分析是車橋耦合振動分析的基礎。PC軌道梁動力特性數值模擬的計算結果與實測結果對比見表2。

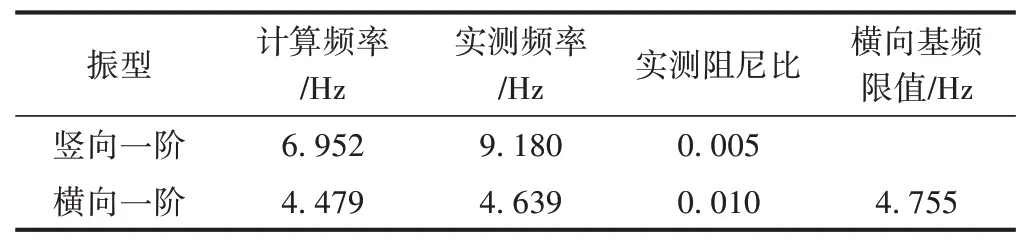
表2 PC軌道梁動力特性數值模擬與實測結果對比

由表2可知：①頻率的實測結果大于數值模擬結果，這說明PC軌道梁實際剛度比模擬計算時采用的剛度要大。②根據鐵運函〔2004〕120號《鐵路橋梁檢定規范》，簡支梁橫向基頻限值取90∕L，其中L為橋梁跨度。對于該測試橋跨，限值為4.755 Hz。實測橫向基頻與限值相當，說明單軌交通系統橫向剛度基本滿足規范要求。

4.4 梁體動力響應

4.4.1 PC軌道梁跨中最大振動位移

四種不平順工況下，PC軌道梁跨中截面最大豎向、橫向動位移隨車速的變化曲線見圖5。可知：①對于跨中最大豎向動位移，實測結果小于模擬計算結果，這與自振頻率反映的PC軌道梁實際剛度大于計算值一致，可見采用PC軌道梁截面計算其動位移能夠滿足單軌交通PC軌道梁設計的安全性要求；而且從圖中可以看出跨中最大豎向動位移受車速的影響不大。②對于跨中最大橫向動位移，鋼梁不平順工況與6級不平順工況的計算結果基本一致，略大于無外部激勵工況；同無外部激勵相比，考慮軌道不平順后，跨中實測最大橫向動位移在車速不大于40 km∕h或不小于60 km∕h時顯著增大，這說明軌道不平順是引起PC軌道梁跨中橫向振動的主要因素；隨著車速增加，跨中最大橫向動位移呈先減后增的趨勢。

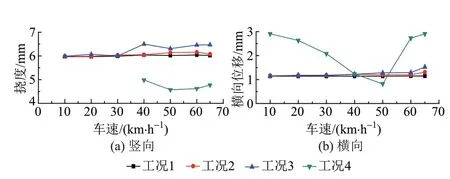
圖5 PC軌道梁跨中最大動位移隨車速的變化曲線

4.4.2 PC軌道梁跨中動位移時程曲線

車輛分別以40、60 km∕h通過時，在工況3條件下，PC軌道梁跨中截面豎向動位移時程位移曲線見圖6。可知：車輛以不同速度過橋時，跨中豎向動位移的振幅均不大，且兩種車速下的振幅幾乎相同。由豎向動位移最大值ymax、最小值ymin可以得出最大豎向位移振幅為|ymax-ymin|=1.17 mm。

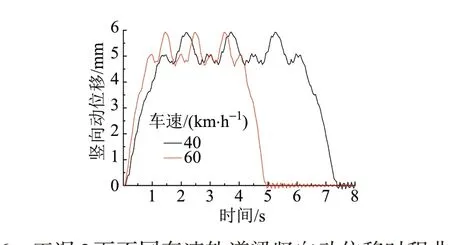
圖6 工況3下不同車速軌道梁豎向動位移時程曲線

基于橋梁振動位移計算跨中截面的沖擊系數K，算 得K=1+|ymax-ymin|∕|ymax+ymin|=1.12；根 據TB 10002—2017《鐵路橋涵設計規范》，算得K=1.09；根據文獻［14-15］試驗測試結果，K=1.08。可見，根據TB 10002—2017的計算結果小于車橋耦合振動模擬計算和測試結果，單軌交通PC軌道梁動力沖擊系數計算宜結合車橋耦合振動分析或試驗測試來確定，采用TB 10002—2017計算得到的沖擊系數須放大處理。

4.4.3 PC軌道梁跨中最大振動加速度

四種不平順工況下，PC軌道梁跨中截面最大豎向、橫向振動加速度隨車速的變化曲線見圖7。可知：①PC軌道梁跨中最大豎向、橫向振動加速度實測結果遠大于不考慮軌道不平順的模擬計算結果，這說明軌道不平順是引起PC軌道梁振動的主要激勵源。②對于跨中最大豎向振動加速度，實測結果基本介于鋼梁不平順工況和6級不平順工況之間；實測的最大豎向振動加速度基本隨車速增加而增大。③對于跨中最大橫向振動加速度，鋼梁不平順工況、6級不平順工況及實測結果比較接近，而鋼梁不平順與6級不平順的差別僅僅在于走行輪軌道不平順的不同，這說明橫向振動主要受軌道梁側面不平順的影響；各工況下的最大橫向振動加速度基本隨車速增加而增大。根據鐵運函〔2004〕120號，最大橫向振動加速度不得超過1.40 m∕s2。車速大于40 km∕h后，PC軌道梁橫向加速度值超過限值，宜降速行駛。

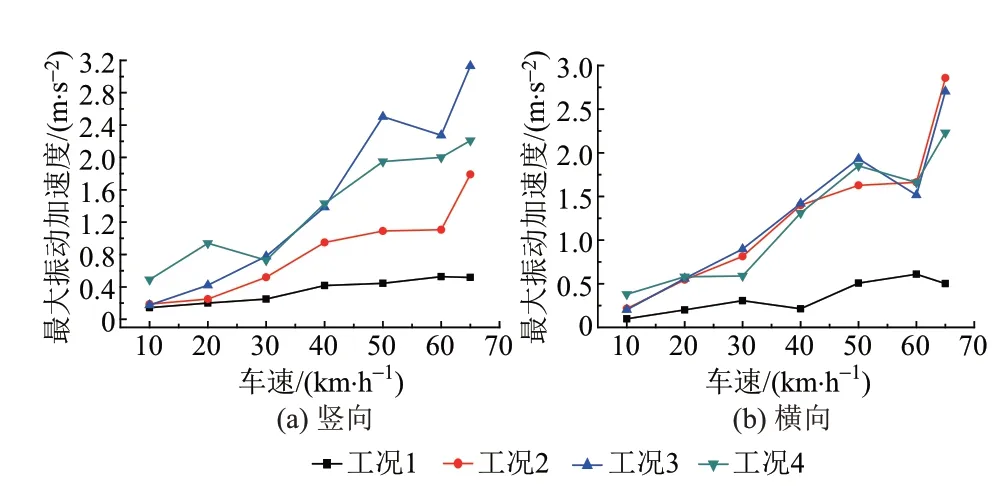
圖7 PC軌道梁跨中最大振動加速度隨車速變化曲線

4.5 機車車輛動力響應

四種不平順工況下，機車車輛的車體最大振動加速度隨車速的變化曲線見圖8。

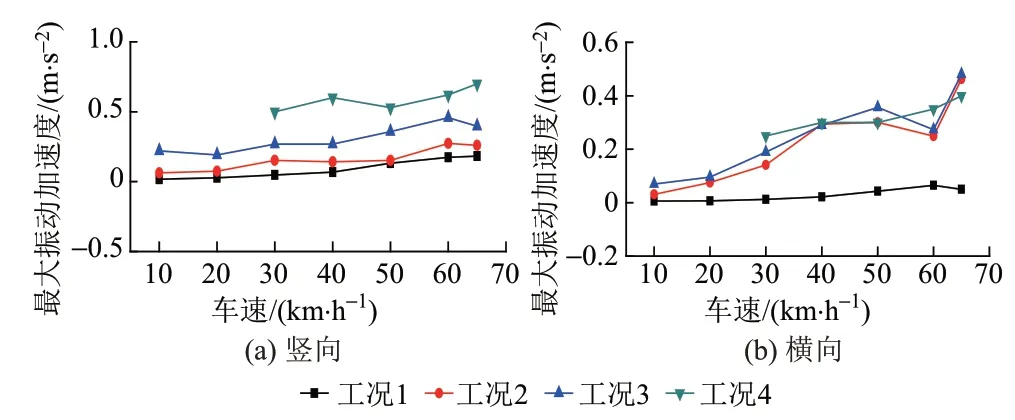
圖8 車體振動加速度隨車速的變化曲線

由圖8可知：①車速大于40 km∕h后，車體最大橫向振動加速度的實測結果基本介于鋼梁不平順工況和6級不平順工況之間。②不考慮軌道不平順的車體最大豎向、橫向振動加速度均低于實測結果，這說明軌道不平順是引起車輛振動的主要激勵源。③車體最大豎向、橫向振動加速度基本隨著車速的增加而增大；車速大于50 km∕h后，車體最大橫向和豎向振動加速度均顯著增大，這與軌道梁振動加速度增長規律基本一致。

5 結論

1）軌道不平順是引起PC軌道梁跨中橫向振動的主要因素。

2）PC軌道梁和車輛的振動加速度隨車速增加而增大。車速大于40 km∕h后，PC軌道梁橫向加速度超過規范限值，宜降速行駛。

3）單軌交通PC軌道梁動力沖擊系數宜結合車橋耦合振動分析或試驗來確定，采用TB 10002—2017計算得到的沖擊系數須放大處理。

本文研究成果對推廣跨座式單軌交通、優化其軌道橋梁設計具有一定的意義和參考價值。