基于跳擴散模型對隨機利率下遠期開始期權定價研究

孫彩靈, 劉麗霞

(河北師范大學 數學科學學院, 石家莊 050024)

0 引 言

隨著經濟的不斷發展，金融衍生品受到了越來越多衍生品交易者的青睞。因此,期權的定價問題也引起了學術界和業界的高度關注。19世紀70年代，Black和Scholes提出了期權定價的B-S模型[1]。B-S模型中假設利率是常數，資產價格服從幾何布朗運動。為了使B-S模型的適用范圍更廣泛，有必要對B-S模型進行擴展。一方面，由于實際生活中的利率是隨機波動的，許多學者對隨機利率下期權的定價進行了研究，例如，2008年，李淑錦等研究了隨機利率下復合期權和重置期權的定價[2]；2015年，韓松研究了隨機利率下亞式期權定價的新方法[3]；2021年，史言研究了隨機利率混合指數跳擴散模型下的期權定價[4].考慮到CIR和Vasicek兩種利率模型中， Vasicek利率模型的均值回歸性更加符合實際，因此,本文假設利率服從擴展的Vasicek模型。另一方面，考慮到突發事件可能會發生，如政府政策的變化、自然災害等，這些都將對金融市場有很大的影響，導致資產價格發生突然的跳動，因此，在模型中加入刻畫資產價格波動的復合泊松過程，能使模型更加切合實際。如2004年，錢曉松研究了跳擴散模型下交換期權的定價[5]；2012年, 李翠香等研究了基于隨機利率下跳-擴散過程的復合期權定價公式[6]；2018年，李藝卓等研究了跳擴散模型下的二選期權定價等[7]；2021年，劉朝暉等研究了跳擴散模型下交換期權定價的Mellin變換方法[8]。

近年來，金融市場交易了大量的奇異期權，如復合期權、障礙期權和彩虹期權等。遠期開始期權是以在事先約定未來某一時刻開始生效，且執行價格為期權生效時刻的標的資產價格的路徑依賴期權[9]。期權生效時刻為，到期日為，執行價格為S(T1)的歐式看漲和看跌遠期開始期權在到期日的收益分別為

c(T,S(T))=max(S(T)-S(T1),0)

p(T,S(T))=max(S(T1)-S(T),0)

迄今為止，有很多關于遠期開始期權的定價研究。2012年，王獻東給出了基于Egarch模型的遠期開始期權定價[10]；2018年，孫慧等給出了帶信用風險的遠期起點期權的定價[11]；2020年，李翠香等研究了基于NIG模型的遠期開始期權的定價[12]。為了豐富遠期開始期權的研究，本文將假設股票價格服從跳擴散模型，并且其收益率和波動率服從關于時間的非隨機函數，在擴展的Vasicek利率模型下，利用跳擴散模型下的Girsanov定理和測度變換的方法推導歐式看漲和看跌遠期開始期權的定價公式。

1 預備知識和引理

以下設(W,F, {Ft},Q)為帶有域流{Ft}的概率測度空間，其中Ω為樣本集合，F為Ω生成的σ域，Q為風險中性測度, {Ft}為本文所涉及到的隨機過程所生成的域流。并且假設資產價格S(t)服從如下隨機微分方程(以下記為SDE(1)):

(1)

無風險利率r(t)服從擴展的Vasicek利率模型(以下記為SDE(2))：

dr(t)=(θt-atr(t))dt+σr(t)dZ(t)

(2)

式中S(t-)表示左極限，為了書寫簡便，下面將S(t-)記為S(t)。W(t)和Z(t)為測度Q下的標準布朗運動，且相關系數為ρ。N(t)為到達參數為λ且獨立于W(t)和Z(t)的泊松過程。Uj(j=1,2,…)表示資產第j次跳躍的跳躍幅度，且Uj為獨立同分布的隨機變量序列，且當j≥1時，Uj服從對數正態分布，即

下面介紹幾個重要引理：

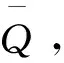
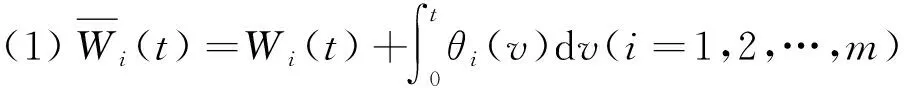
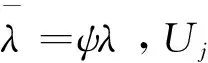
引理1.3[2]假設隨機利率r(t)服從SDE(2)，則

(3)

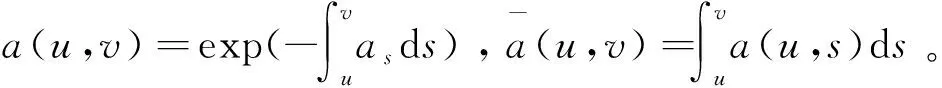
基于引理1.1滿足的條件，運用鞅方法也可以獲得貼現債券的價格，因此有以下引理。

引理1.4[2]當利率滿足SDE(2)時，到期日為T的貼現債券t時刻的價格B(t,T)滿足

(4)

引理1.5假設資產價格S(t)服從SDE(1)，則有以下表達式:

(5)

2 隨機利率跳擴散模型下遠期開始期權的定價

定理2.1設標的資產S(t)服從SDE(1)，利率r(t)服從SDE(2)，則生效日為T1，到期日為T，執行價格為S(T1)的歐式看漲遠期開始期權在0時刻的價格為：

式中N(·)表示標準正態隨機變量的累積分布函數，且

證明

由風險中性定價原理可得:

(6)

首先計算I1。取

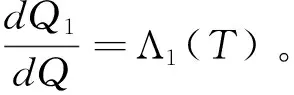
(7)

那么

從而在Q1下，Uj的密度函數為:

進而可以得到Q1下，lnUj的密度函數為：

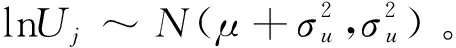
由引理1.1可得:

I1=EQ[Λ1(T)S(0)I{S(T)>S(T1)}]=S(0)EQ1[I{S(T)>S(T1)}]

(8)

將式(7)代入式(5)，得:

(9)

將式(7)代入式(3)，得:

(10)

結合式(4)、式(9)和式(10)可得資產價格在Q1下服從的方程為:

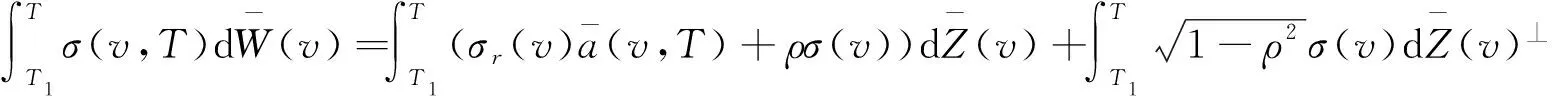
(11)

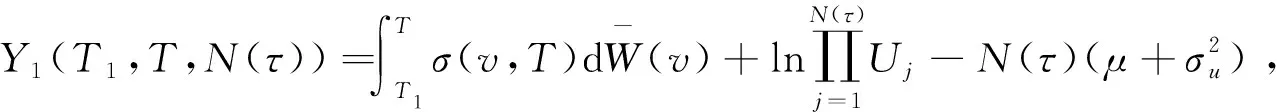
由式(11)可得:

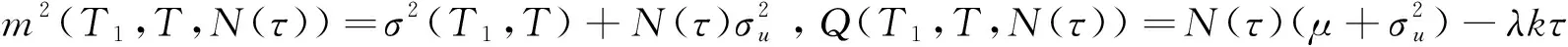
由式(8)可得:

EQ1[I{S(T)>S(T1)}|N(τ)=n]

=N(d1)

(12)

由式(8)和式(12)可得:

(13)

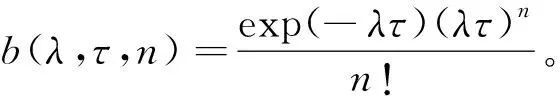
下面計算I2。取

式中，

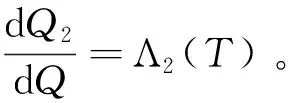
由引理1.2可得, 在新測度Q2下，有:

(14)

(15)

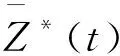
由引理1.1可得:

I2=S(0)EQ[H(0,T1,T)Λ2(T)I{S(T)>S(T1)}]

(16)

由引理1.3和引理1.4可得，資產價格S(T)在Q2下的方程為：

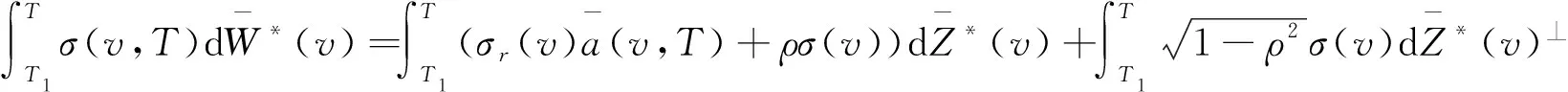
(17)

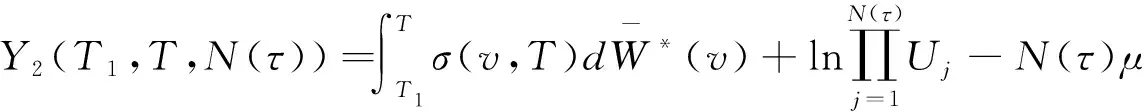
由式(17)可得:

由式(16)可得:

EQ2[I{S(T)>S(T1)}|N(τ)=n]

=N(d1-m(T1,T,n))

=N(d2)

(18)

由式(16)和式(18)可得:

(19)

I2得證。

結合式(13)和式(19)，定理2.1得證。

推論2.1在定理2.1的條件下，歐式看跌遠期開始期權在0時刻的價格為:

證明：類似定理2.1可證。

3 數值實驗

在上述分析中，分別得到了遠期開始看漲和看跌期權的定價公式。本部分將利用Matlab軟件分別給出各參數對期權價格的影響。為了便于計算，以下假設關于時間的確定函數θt、σr(t)、σ(t)和at均為常數，分別記為θ、σr、σ、a，且各參數對應的值如表1所示。

表1 相關參數值

在以上參數假設的基礎上，利用Matlab軟件作圖，分別得到了變量T、a、μ、λ、θ和σr的變化對期權價格的影響，如圖1～圖6所示。

圖1中曲線1給出了隨機利率跳擴散環境下遠期開始看漲期權的價格隨時間變化的圖像，曲線2表示普通歐式遠期開始看漲期權的價格隨時間變化的圖像，通過對比可得，隨機利率跳擴散環境下的期權價格遠比普通期權價格高，因此，研究隨機利率跳擴散環境下的期權定價更具有現實意義。

圖2～圖4分別表示變量a、μ和λ對隨機利率跳擴散模型下遠期開始看漲期權的價格影響，由圖像可得，期權價格隨a、μ和λ的增大而增大，隨θ和σr的增大而減小。

圖5和圖6分別表示變量θ和σr對隨機利率跳擴散模型下遠期開始看漲期權的價格影響，由圖像可得，期權價格隨θ和σr的增大而減小。

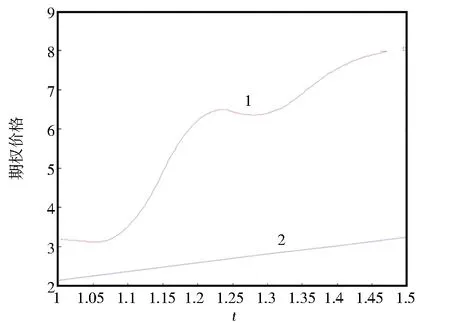
圖1 遠期開始看漲期權價格圖像

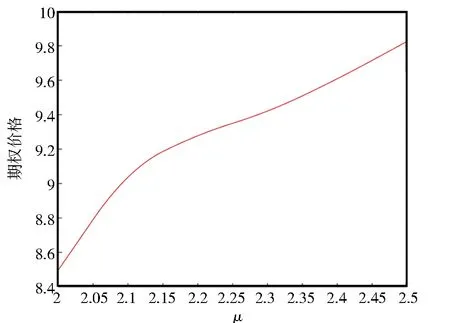
圖3 期權價格與μ的關系

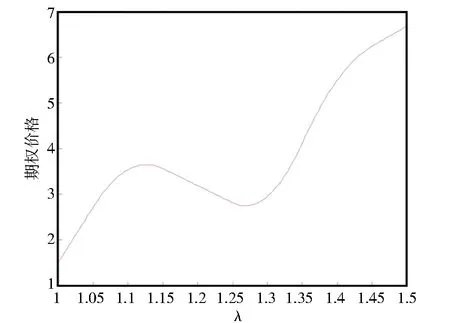
圖4 期權價格與λ的關系

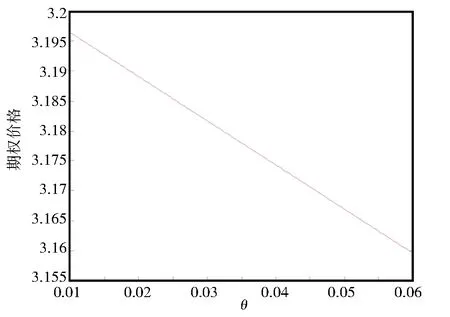
圖5 期權價格與θ的關系

4 總 結

首先假設資產價格服從跳擴散模型下的幾何布朗運動，且無風險利率服從擴展的Vasicek利率模型，模型中的布朗運動相關系數為ρ。其次利用跳擴散模型下的Girsanov定理和測度變換的方法得到歐式看漲和看跌遠期開始期權的定價公式。最后通過數據分析得到隨機利率跳擴散模型下遠期開始看漲期權價格比普通遠期開始看漲期權價格高，并分析了各個變量對期權價格的影響。