高溫高壓封隔器實驗室防護墻的抗爆性分析*

易先中 任 路 王含陽 馬蘇南,3 姜永奎 羅 濤 胡佩艷

(1.長江大學機械工程學院 2. 中國石油集團渤海鉆探工程有限公司工程技術研究院 3. 長江大學非常規油氣湖北省協同創新中心)

0 引 言

防爆墻是一種有效的被動防爆結構，它能降低爆炸荷載，保護主體建筑物及建筑物外圍工作人員的人身安全。

1984年，錢偉長[1]最先對不同形狀物體擊穿靶板進行力學分析，得到了不同形狀物體撞擊靶板的過程分析及力學相關公式。1992年，孫韜等[2]首先研究剛性球形彈丸對間隔靶或多層靶的侵徹問題，建立了彈丸與靶體相互作用模型，由該模型可計算出相互作用的表面在每個時間增量時的變化狀態，以及可獲得靶的阻力，將這些參數代入到彈丸的運動方程中，可得到一個完整的彈丸在擊穿靶或未擊穿靶時的彈道軌跡。2002年，陳劍杰等[3]首次使用DYNA軟件計算得到爆炸載荷，并采用有限元優化設計技術分析了空心圓柱體鋼筋混凝土結構的抗爆性能，其與爆炸試驗相比，誤差在14%左右，計算得出的結構響應和破壞規律可供工程設計參考。2009年，E.FERRI[4]研制了一種帶有高速攝影和直接沖擊霍普金森壓力棒的氣槍，用于實驗室規模的高速沖擊試驗。該模型為研究夾層板在沖擊載荷作用下的響應提供了有參考價值的本構模型。2004年，LI W.等[5]為了研究金屬和纖維增強聚合物交替層組成的層壓板對沖擊的反應，開發了一個基于連續損傷的模型并在Abaqus軟件中實現，計算出鋁的彈道極限，與Abaqus有限元分析彈道極限平均誤差為3.2%左右。

為了研究井下封隔器防護墻在地面測試試驗中，不同形狀爆炸物對防護墻的侵徹深度，本文通過解析計算與有限元分析兩種方法相結合，分析了8種常規爆炸物(M8螺栓、M10螺栓、M10螺母、堵頭、鋼管、圓柱體、三棱柱和長方體)和6種極端爆炸物(四棱錐、?15 mm彈頭狀、?16 mm彈頭狀、?17 mm彈頭狀、?18 mm彈頭狀、?20 mm彈頭狀)在不同爆炸工況下對防護墻的侵徹情況。本文計算了爆炸物對兩種夾層防護墻(含玻纖、無玻纖)結構的侵徹深度，分析了兩種結構防護墻的抗爆性能。通過對穿透能力強的彈頭狀爆炸物侵徹深度進行分析，計算出能夠擊穿防護墻的彈頭狀爆炸物的尺寸，進而實現了對封隔器實驗室防護墻抗爆性能的優化，優化結果能夠對工作人員的人身安全提供有效的保障。

1 初始條件分析

1.1 試驗間概述

封隔器試驗間如圖1所示，長度12.47 m，寬度3 m，采用20根立柱分布在四周，支撐雙層防護裝置的2個導軌，兩端用兩根橫梁連接。立柱下部與預埋鋼板焊接，上部與導軌用螺栓緊固，成為一體。試驗間防護墻采用雙層鋼板，四周夾層用混凝土或者混凝土與玻璃纖維混合灌注，頂端采用電動移動的雙層防護鋼板進行防護。采用工業遙控器及控制箱手動控制的兩種控制方式，方便可靠，最大開合6 m，滿足工具的吊入。試驗間發生爆炸時，處于封閉狀態。封隔器處于試驗間中間位置，與防護墻最近距離1.5 m。為了最大程度計算防護墻的抗爆性能，爆炸物均垂直撞擊防護墻。

圖1 封隔器試驗間Fig.1 Packer test room

1.2 防護墻結構及參數

封隔器防護墻由前后鋼板和混凝土(或玻璃纖維增強混凝土)組合而成，總厚度為100 mm，前后使用6 mm厚的鋼板，中間夾層使用厚度88 mm的混凝土材料或者玻纖增強混凝土材料。使用的C60無玻纖混凝土的材料參數為：密度2 440 kg/m3，屈服強度38.5 MPa，剪應力4.1 MPa；含5%玻纖的C60混凝土的材料參數為：密度2 300 kg/m3，屈服強度60.0 MPa，剪應力5.0 MPa。防護墻的具體參數如表1所示。

表1 鋼的材料參數Table 1 Specification of steel materials

1.3 爆炸驅動的爆炸物撞擊時速度

爆炸后，爆炸物撞擊防護墻初始狀態有4種工況：工況1為溫度370 ℃、氣壓70 MPa；工況2為溫度370 ℃、液壓70 MPa；工況3為溫度220 ℃、氣壓105 MPa；工況4為溫度220 ℃、液壓155 MPa。

物體由于內外壓力不同，在爆炸后產生壓力能為[6]：

NP=pA1S

(1)

式中：p為爆炸時爆炸物受到的壓力，MPa；A1為壓力作用在爆炸物上的面積，m2；S為爆炸瞬間最大壓力作用下的距離，m，其中工況1作用距離S=0.15 m，工況2作用距離S=0.20 m，工況3作用距離S=0.30 m，工況4作用距離S=0.40 m。

飛出爆炸物的動能為：

(2)

式中：m為爆炸后飛出爆炸物的質量，kg；vr為爆炸后飛出爆炸物的速度，m/s。

根據動能守恒，結合式(1)和式(2)，壓力能全部轉化為動能。通過上述公式可以求出物體速度范圍[7]。

爆炸物在向外運動過程中受到空氣阻力的影響，速度會逐漸減小，速度衰減規律為：

(3)

式中：v0為爆炸物撞擊墻體的速度(如表2所示)，m/s；CD為氣動阻力系數，取0.5；ρa為空氣密度，取1.29 kg/m3；A為爆炸物迎風面積，m2；R為飛行距離，取1.5 m(爆炸時封隔器與防護墻距離為1.5 m)。

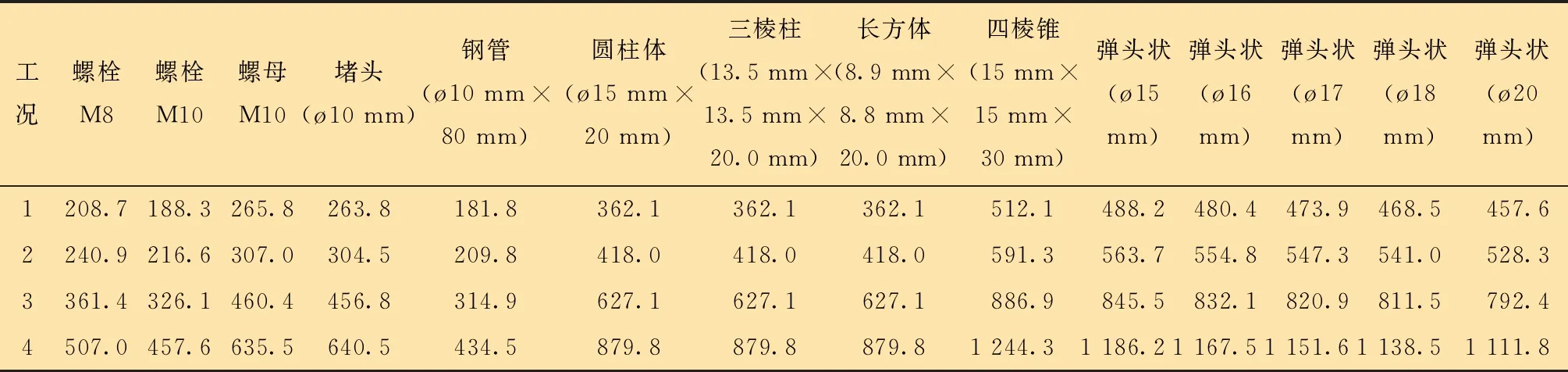
表2 爆炸物撞擊墻體速度 m/s

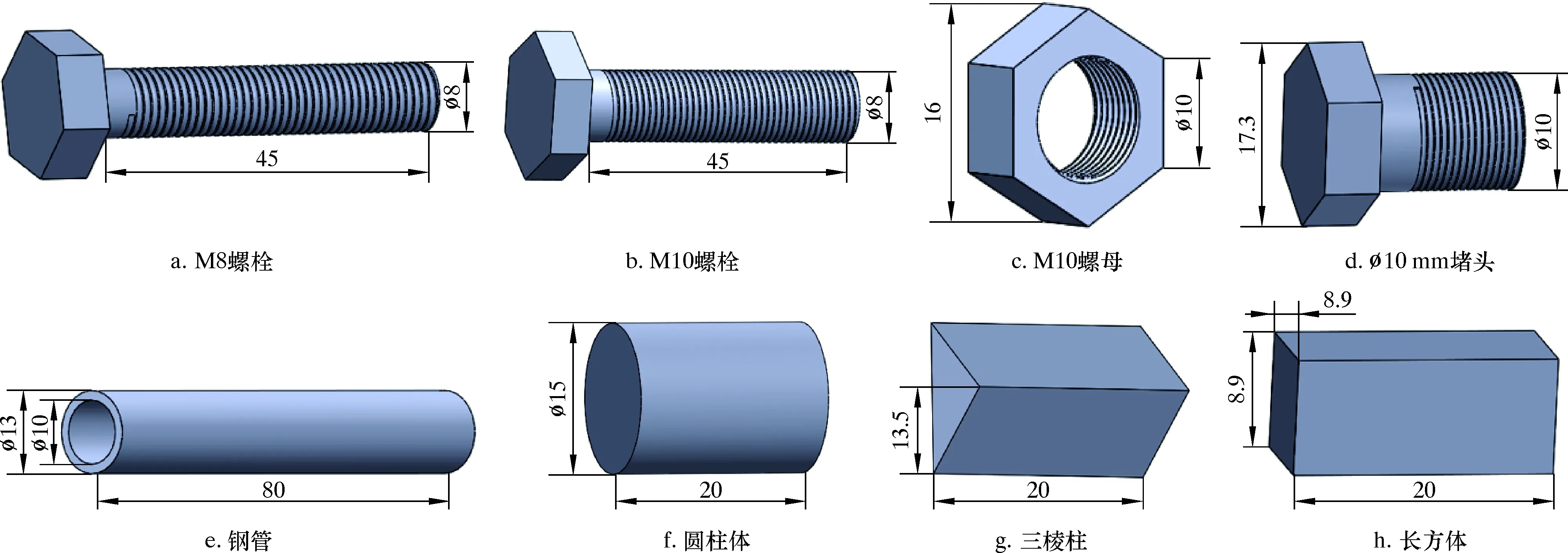
圖2 8種常規爆炸物Fig.2 8 conventional explosives

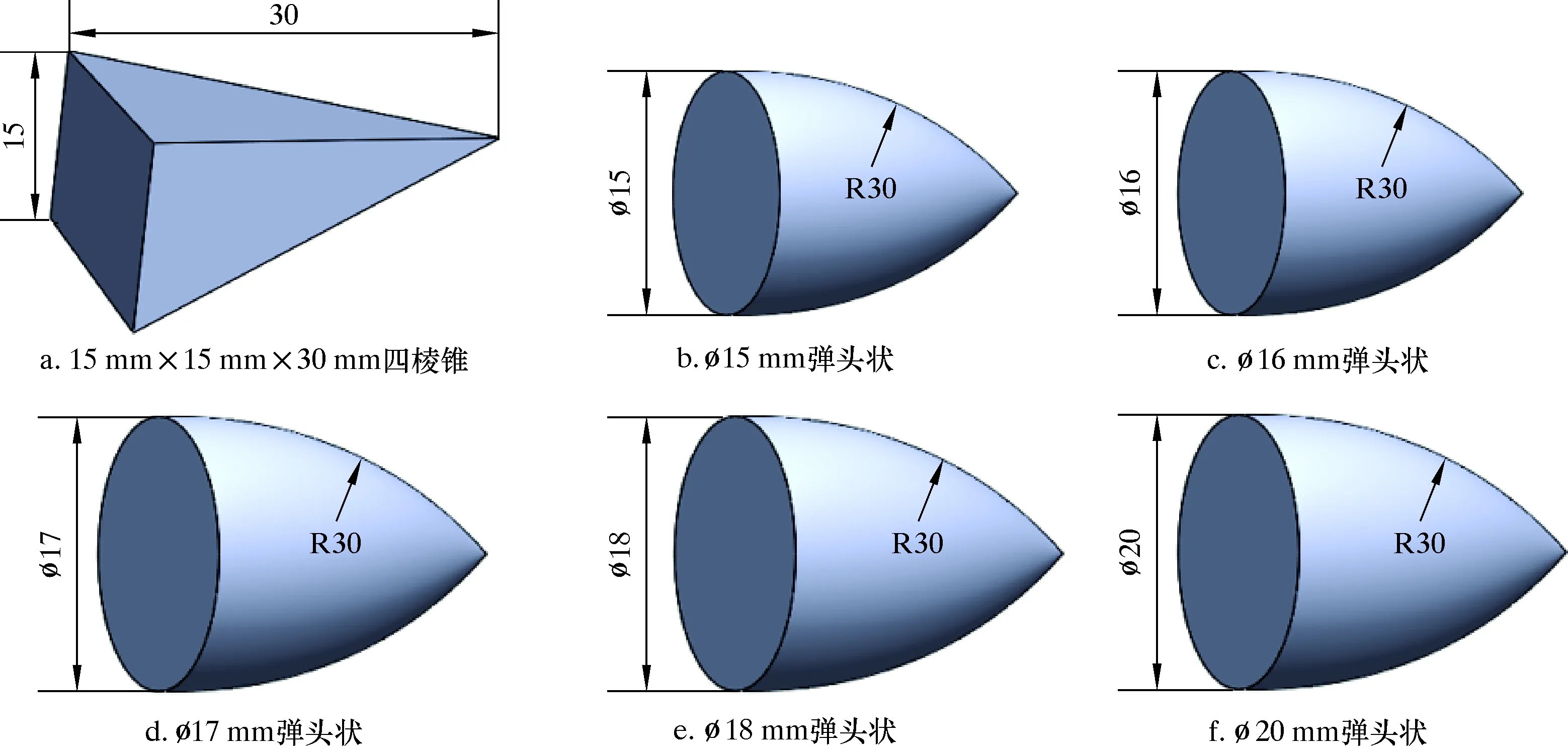
圖3 6種極端爆炸物(彈頭狀)Fig.3 6 extreme explosives (bullet shaped)

2 侵徹深度計算

已知爆炸物的初始速度，分析防護墻的抗爆性能，必須求出爆炸物在各個階段的能量消耗，以及各階段的速度變化。通過計算求出爆炸物侵徹前鋼板、侵徹中間夾層和侵徹后鋼板等3個階段消耗的能量及其剩余速度。剩余速度為0時，求出爆炸物侵徹的位移。

假設：①爆炸物對防護墻產生侵徹過程中逐層侵徹，并且在侵徹后沒有回彈現象；②防護墻在侵徹過程中只發生局部穿孔耗能，忽略由變形或者發熱現象造成的整體耗能；③平頭爆炸物在侵徹防護墻過程中為剛體，不發生變形[8-10]。

2.1 平頭爆炸物

2.1.1 爆炸物侵徹前鋼板階段

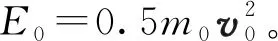
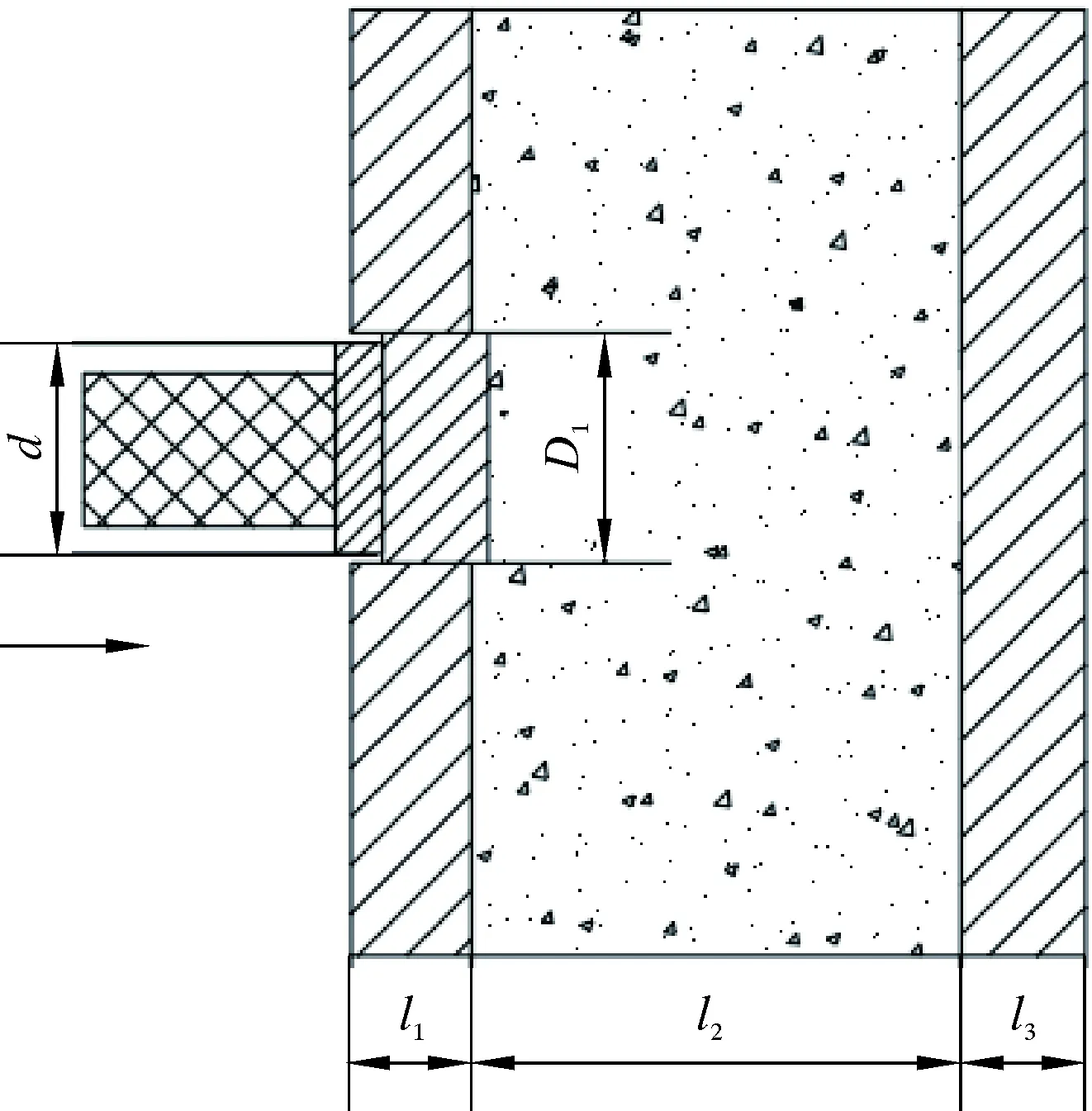
圖4 爆炸物侵徹前鋼板過程Fig.4 Process of explosive penetrating front steel plate

m0v0=(m0+m1)v1

(4)

式中：m1為變形體的質量，g；v1為共同速度，m/s。

變形體的質量[8]可以表示為：

m1=0.25πD2l1ρ1

(5)

式中：ρ1為鋼板的密度，kg/m3。

對于變形體直徑D，有：

(6)

式中：d為爆炸物撞擊面直徑，m；σd為爆炸物的動態屈服強度，MPa；ρ為爆炸物密度，kg/m3。

當爆炸物與變形體以相同的速度前進過程中，會對鋼板造成剪切破壞，在侵徹鋼板過程中存在能量消耗，剪切力做功：

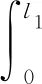
(7)

式(7)中的剪切力采用熱塑性模型[7]，即：

(8)

式中：τm為鋼板的最大剪切力，MPa；γi為τm對應的剪應變；n為加工硬化指數。

根據屈服準則，假設：

(9)

式中：σm為鋼板的拉伸極限，MPa。

聯立式(7)、式(8)和式(9)可得侵徹鋼板過程中的能量消耗：

(10)

爆炸物在第一階段消耗的能量為：

(11)

比較E0和E1的大小，如果E0小于或等于E1，結合式(4)～式(11)，可知爆炸物沒有穿過前鋼板,計算爆炸物侵徹厚度L：

(12)

如果E0大于E1，爆炸物穿過前鋼板繼續侵徹防護墻，此時第一階段侵徹厚度為l1=6 mm。爆炸物在第一階段的剩余速度為：

(13)

2.1.2 爆炸物侵徹中間夾層階段

爆炸物侵徹中間夾層階段(即第二階段)力學模型如圖5所示。爆炸物在侵徹夾層過程中的平均壓應力為：

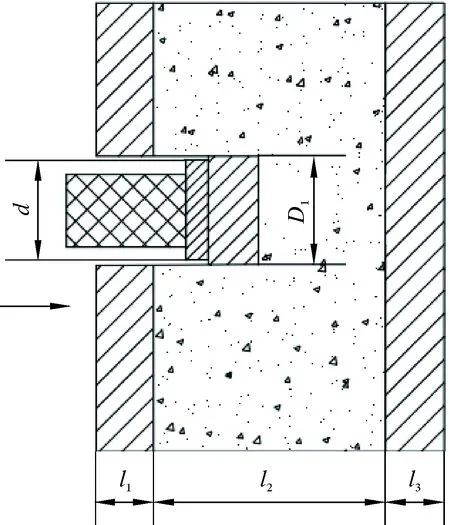
圖5 爆炸物侵徹夾層過程Fig.5 Process of explosive penetrating interlayer

(14)

式中：σe為墻體彈塑性變形引起的準靜態阻力，MPa；ρ2為復合材料墻體的密度，kg/m3；β為與爆炸物形狀相關的系數，β=2；v2為爆炸物侵徹墻體的初始速度，第二階段的初始速度等于第一階段剩余速度。

爆炸物侵徹墻體過程中的能量消耗為：

(15)

式中：A為侵徹鋼板爆炸物頭部截面面積，m2。

聯立式(14)和式(15)，可得第二階段消耗的能量為：

(16)

比較E0-E1與E2的大小，如果E0-E1小于或等于E2，爆炸物沒有穿過中間混凝土夾層，此時侵徹厚度L為：

(17)

如果E0-E1大于E2，爆炸物穿過中間混凝土夾層繼續侵徹后鋼板，此時爆炸物第二階段侵徹厚度為l1+l2=96 mm。爆炸物在第二階段的剩余速度為：

(18)

2.1.3 爆炸物侵徹后鋼板階段

爆炸物侵徹后鋼板階段(即第三階段)力學模型如圖6所示。

圖6 爆炸物侵徹后鋼板階段Fig.6 Stage of explosive penetrating back steel plate

爆炸物侵徹后鋼板過程中變形體質量為[9-10]：

(19)

式中：m2為變形體2的質量，kg；D2為變形體2的直徑，m；ρ3為后鋼板密度，kg/m3。

爆炸物與變形體1和變形體2達到共同速度，由動量守恒定律有：

(20)

消耗的能量為：

(21)

在剪切力做功階段消耗的能量為：

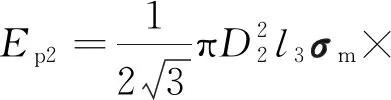
(22)

此階段消耗的能量為：

E3=Ep1+Ep2

(23)

比較E0-E1-E2與E3的大小，如果E0-E1-E2小于或等于E3，爆炸物沒有穿過后鋼板，此時爆炸物侵徹厚度L為：

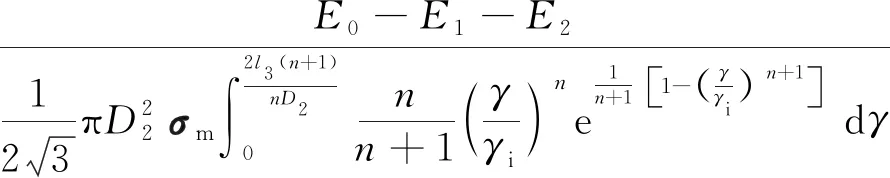
(24)

如果E0-E1-E2大于E3，爆炸物穿過后鋼板，擊穿防護墻。爆炸物在第三階段的剩余速度為：

(25)

2.2 錐形或卵形爆炸物

2.2.1爆炸物侵徹前鋼板階段

根據穿甲力學彈體穿透薄板的穿透能公式[1]，第一階段彈體初始動能和侵徹鋼板耗能分別為：

(26)

式中：R1為爆炸物侵徹前鋼板鐓粗半徑，m，計算方法見式(6)；σy為鋼板的屈服應力，MPa；m為爆炸物質量，kg。

比較E0與E1的大小，如果E0小于或等于E1，則爆炸物沒有穿過前鋼板，此時爆炸物侵徹厚度L為：

(27)

如果E0大于E1，爆炸物穿過前鋼板繼續侵徹防護墻進入第二階段。爆炸物在第一階段的侵徹厚度l1=6 mm，剩余速度為：

(28)

2.2.2 爆炸物侵徹中間夾層階段

根據郁時煉等[11]卵形彈垂直侵徹混凝土介質的量綱分析，撞擊混凝土侵深的工程表達式為：

(29)

式中：v1為撞擊速度，m/s；σ為混凝土屈服應力，MPa；m為爆炸物質量，kg；R1為爆炸物半徑，mm。

爆炸物第二階段侵徹厚度L=l1+l2。

當計算第二階段侵徹厚度l2>88 mm時，爆炸物會擊穿中間混凝土夾層，此時令l2=88 mm，根據式(29)可求出爆炸物擊穿中間夾層的速度v2：

(30)

爆炸物在第二階段消耗的能量為：

(31)

爆炸物在第二階段的剩余速度為：

(32)

2.2.3 爆炸物侵徹后鋼板階段

第三階段彈體侵徹鋼板耗能為：

(33)

式中：R2為爆炸物侵徹后鋼板鐓粗半徑，m，計算方法如式(6)。

比較E0-E1-E2與E3的大小，如果E0-E1-E2小于或等于E3，爆炸物沒有穿過后鋼板，此時侵徹厚度L為：

(34)

如果E0-E1-E2大于E3，爆炸物穿過后鋼板，擊穿防護墻。爆炸物在第三階段的剩余速度為：

(35)

3 有限元計算結果

3.1 建立模型

防護墻兩側采用雙層防護鋼板進行防護，鋼板厚度6 mm，在鋼板中間加入混凝土墻體或者混凝土與玻璃纖維混合夾層，厚度為88 mm，總厚度為100 mm。設置標準爆炸物破片為45號鋼，爆炸物零件材質為304不銹鋼，前后鋼板材料為Q235鋼，材料具體參數如表1所示。

3.2 施加約束條件并求解計算

為了準確模擬爆炸物侵徹防護墻結構的真實響應，將防護墻的周圍表面設置為固定約束，正面和背面為自由面，墻體的約束為四邊固支，給爆炸物施加初始速度約束，添加墻體總變形[12-16]。爆炸物侵徹數據如表3所示，其中最大侵徹深度如圖7所示。

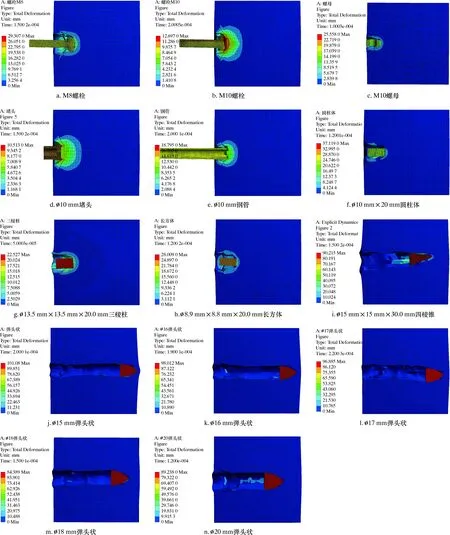
圖7 爆炸物最大侵徹深度Fig.7 Maximum penetration depth of explosive

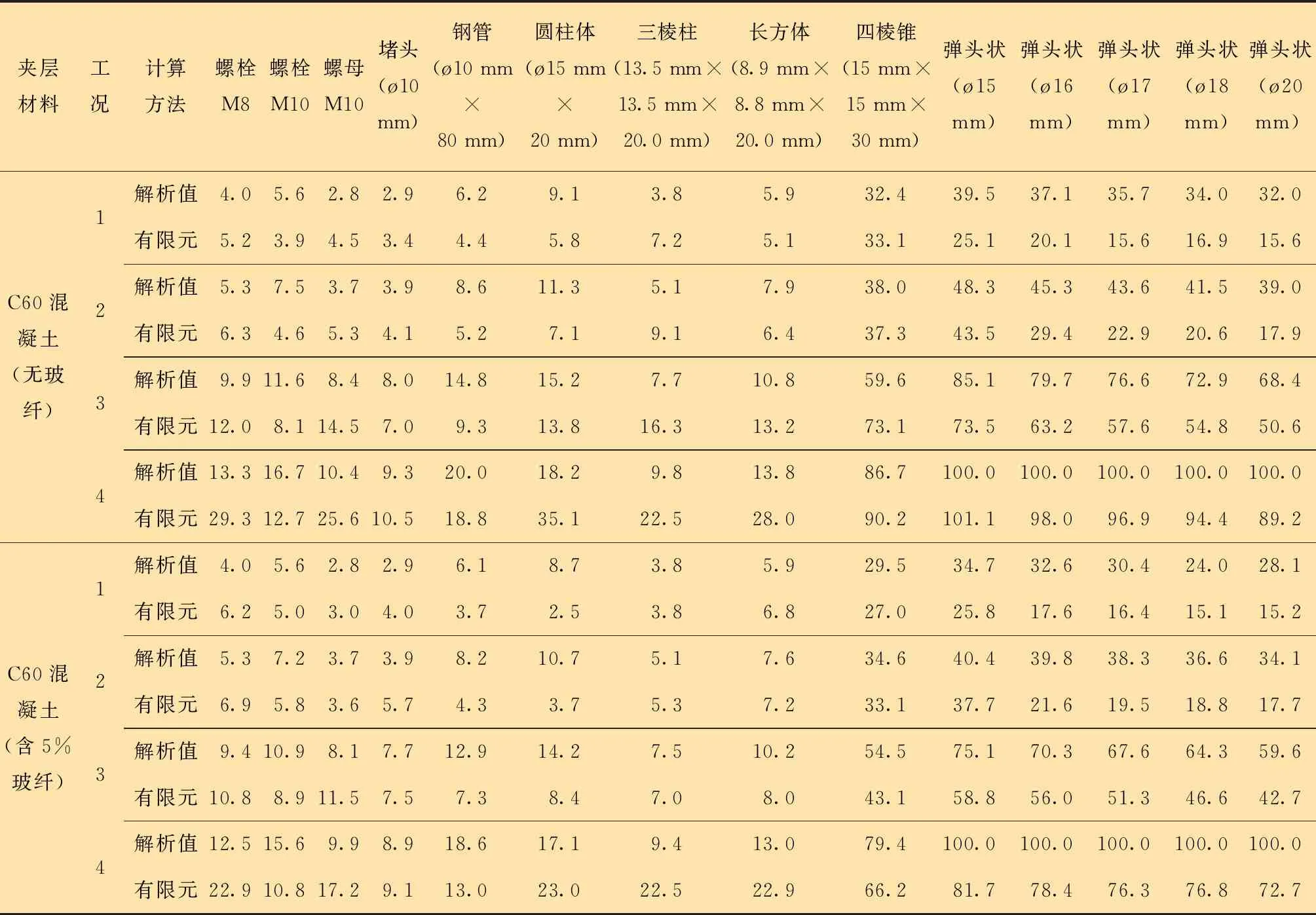
表3 爆炸物侵徹深度mm

結合表3和圖7可以看出，在溫度370 ℃、壓力70 MPa(氣壓、液壓)以及溫度220 ℃、氣壓105 MPa 或液壓155 MPa等4種工況下，在溫度220 ℃、液壓155 MPa 時，爆炸物對防護墻的破壞最為嚴重。在相同工況下，含5%玻纖增強混凝土防護墻的抗爆性能更好。爆炸物侵徹深度折線圖如圖8所示。分析圖8可知，爆炸物對含玻纖增強混凝土結構防護墻的侵徹深度平均比混凝土結構防護墻的侵徹深度小22.1%，即使用玻纖增強混凝土結構防護墻的抗爆性能更好。

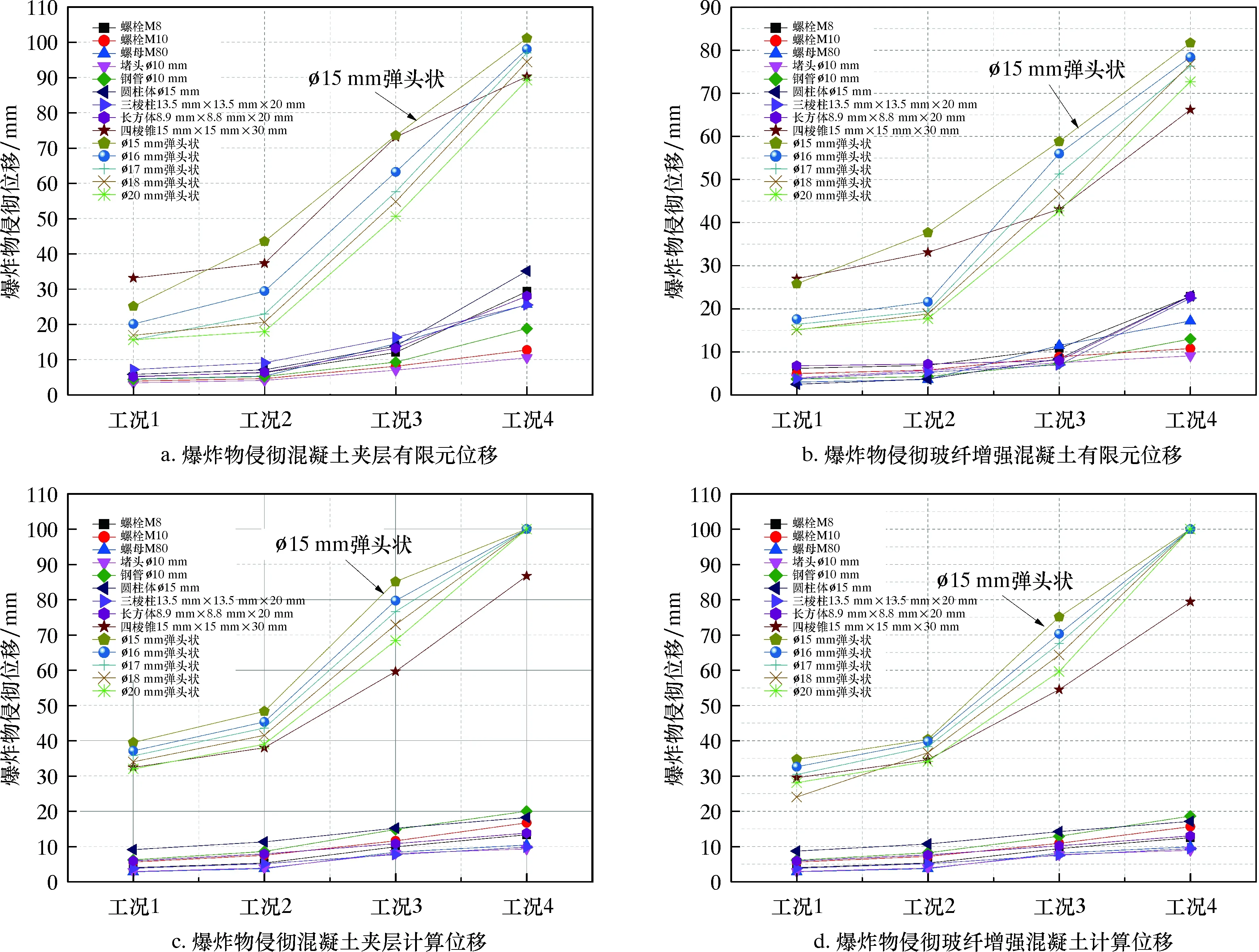
圖8 爆炸物侵徹防護墻位移曲線Fig.8 Displacement of explosive penetrating protective wall

4 數據誤差分析

為了研究解析值和有限元計算帶來的誤差，運用前述計算方法對帶裝甲鋼背板的鋼纖維混凝土靶進行侵徹試驗[17]對比，以判斷本文計算方法的誤差大小。

馮君等[17]采用兩種彈頭進行侵徹試驗：①穿甲彈，其彈芯尖卵形頭部曲率半徑比值為3，直徑為10.8 mm，質量為30.0 g；②1∶4.7底推式桿式模擬彈，即長桿彈，直徑為6 mm，彈頭長度13 mm，質量為44.5 g。彈頭尺寸模型如圖9所示。

圖9 彈頭尺寸模型Fig.9 Bullet size model

侵徹試驗裝置如圖10所示，主要包括槍彈發射裝置、彈托回收裝置、測速裝置和帶裝甲鋼背板的鋼纖維混凝土靶。鋼纖維混凝土靶體的直徑為100 mm，厚度有50和100 mm兩種，背板采用603裝甲鋼。對于裝甲鋼材料的本構模型，本文采用Johnson-cook模型，這是一種考慮壓力相關性、應變率強化模型和溫度軟化效應的理想彈塑性強化模型。混凝土厚度也分為30和60 mm兩種。誤差對比分析結果如表4所示。

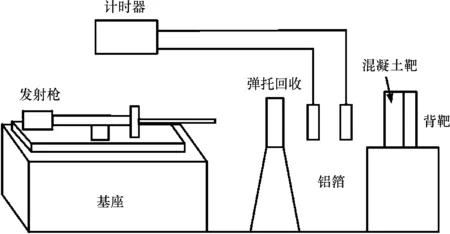
圖10 侵徹試驗裝置Fig.10 Penetration test device

表4 復合靶侵徹有限元結果與試驗結果對比Table 4 Comparison of finite element calculation and test results of composite target penetration

與帶裝甲鋼背板的鋼纖維混凝土靶抗侵徹試驗及數值模擬數據進行對比，結果表明，運用本文方法最大解析計算誤差為20.6%，最大有限元計算誤差為21.1%，說明本文計算方法對防護墻的抗爆性能分析偏于安全。造成誤差的原因有：①公式中一些參數值的確定存在誤差，帶入公式計算后導致侵徹深度偏大；②沒有考慮爆炸物在侵徹防護墻過程中發生的熱損耗，也導致了侵徹深度偏大；③在有限元分析中，有些材料參數設置存在差異，導致最終結果不同。

5 結論及建議

(1)封隔器測試試驗中的8種常規爆炸飛出物，直徑15 mm、長20 mm的圓柱體對防護墻的侵徹深度最大為35.1 mm，說明防護墻具有足夠的抗常規爆炸物的能力。

(2)在相同工況下，含5%玻纖增強混凝土夾層防護墻比無玻纖混凝土防護墻的抗爆性能相對增強21.1%。

(3)封隔器測試試驗中的5種極端爆炸物，以?15 mm彈頭狀爆炸物對防護墻的侵徹深度最大。對無玻纖混凝土防護墻的侵徹深度101.1 mm，達到防護墻的極限；而對含5%玻纖增強混凝土夾層防護墻的侵徹深度為81.7 mm，滿足安全裕度要求。

(4)建議選用前后6 mm厚鋼板、中間夾層含5%玻纖增強混凝土及總厚度為100 mm的防護墻設計方案。

(5)文中的解析計算結果與試驗數據進行對比，誤差范圍為1.5%～20.6%，驗證了本文方法的正確性、有效性和可靠性。