層狀場地中粘彈性人工邊界古城墻地震反應分析

唐曉榮 周占學,2* 于 爽 李 楊 袁曉聰

(1.河北建筑工程學院，河北 張家口 075000；2.河北省土木工程診斷、改造與抗災重點實驗室)

0 引 言

古城墻是我國歷史上建筑文化的傳承，是古代勞動人民的智慧的象征，是歷史傳承的使者，對其抗震研究有助于古建筑的保護與發展，高衡[1]等人對西安城墻磚進行分析，研究其組成成分及力學性能，得出現存古城磚機械性能一般，高大峰[2]等人對西安城墻進行實驗研究，分析結構下地震激勵下的動力反應和動力特征.劉琨[3-4]等人對高昌故城內城墻墻體進行現場脈動實驗，分析城墻不同部位速度放大效應，研究動力響應特征，為城墻抗震加固提供參考依據.

以張家口大境門古城墻為參考，利用ABAQUS有限元軟件建立古城墻模型和土-古城墻模型，采用劉晶波教授等人粘彈性人工邊界理論[5-7]添加人工邊界，文中進行模態分析，得到兩個模型的自振頻率和周期，再選取El-Centro、Taft、天津波三種地震波進行地震分析，得到兩個模型的位移時程曲線和加速度位移時程曲線.

1 有限元模型建立

1.1 模型概況

大境門的古城墻是用夯土筑建而成，土層比較均勻、緊密，處于堅硬和應訴狀態，土體夯筑后在夯土的兩側包上數層的青磚，城墻磚尺寸大于普通的燒結磚，城墻磚之間的接縫采用白灰漿砌筑，白灰漿在古代是將糯米加入到石灰砂漿中攪拌而成，城墻地基多采用條石地基，基礎埋深1.5米，模型全長100米，高度10米，城墻下部寬度為6.4米，上部寬為5米，中間門洞為拱形門，整體寬度為5米，高度為6.5米，城墻下部土層取長度100，土層厚為40米.有限元模型如圖1所示.

圖1 有限元模型

1.2 模型材料及參數

大境門古城墻結構采用的是內部夯土筑建外部包磚的形式，屬于磚土結合，通過對城墻土的實驗研究8]得到古城墻夯土材料參數如下表所示：

(a)古城墻模型 (b)土-古城墻模型

表2 城墻磚砌體材料參數表

在進行土—古城墻相互作用分析時，截取城墻下一定范圍的土層，在不同土層施加相應的人工邊界來替代古城墻結構下部無限土域，由于大境門城墻附近的地質資料不夠充分，現有條件不允許進行鉆孔勘察，所以采用天保·蔚州城巖土工程勘察的蔚縣縣城的地質勘察資料，其土層參數見下表：

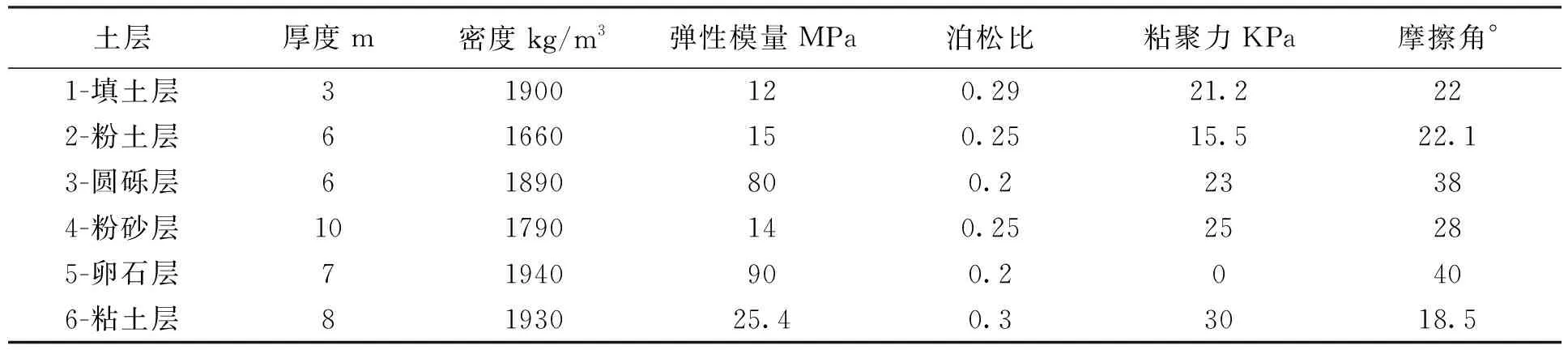
表3 層狀土層參數

1.3 本構關系

城墻結構采用外部包磚、內部夯土的形式，有效提高城墻防水能力，防止風雨侵蝕，同時提高城墻的堅固程度.由于城墻外包磚的極限強度和彈性模量遠大于內部夯土，考慮包磚與夯土相互作用，將包磚砌體模型簡化成各向同性且材料均勻的線彈性模型，城墻夯土采用Mohr-Coulomb模型.

由于城墻下的土體材料、參數不同，對應采用本構關系也不同，考慮到土體的動力非線性，文中采用了等效線性模型，該模型通過迭代來近似反應土體的非彈性和非線性，是土層地震動反應分析的主流方法，在水平成層場地應用廣泛.

利用ABAQUS提供的用戶子程序作為二次開發平臺，在輸入文件中，使用關鍵詞定義用戶材料，在用戶材料子程序中可以實現定義材料的本構關系，文中利用其基本原理編制Fortran程序，在ABAQUS有限元軟件中調用子程序，作為土體的本構關系.

1.4 人工邊界的條件及選擇

人工邊界是對人們在處理無限連續介質問題時人為引用的虛擬邊界，目的在于簡化問題，便于計算，現實情況下，建筑結構并不是處在封閉的空間中，它是半無限的狀態之下，在有關有限元模擬分析中，有限元軟件只能將模型定在一定范圍之內，模型所包含的范圍場地稱之為自由場，從而引入了人工邊界的研究，為了確保分析結果的精確性和嚴謹性，國內外眾多學者進行了大量的研究與分析，并取得了許多有價值的成果，本文采用的是劉晶波教授粘彈性人工邊界理論.其中彈簧元件的彈性系數KB和阻尼系數CB計算公式如下：

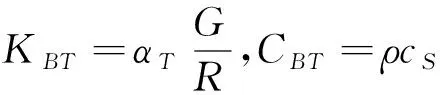
其中，G為介質的剪切模量；ρ為介質的質量密度；R為散射源到人工邊界節點的距離，cs是介質中的S波波速，cp是介質中的p波波速，參數α為人工邊界參數.取值參考下表4

表4 粘彈性人工邊界αT、αN取值范圍

2 結構動力特性分析

模態分析是一種研究結構動力學特性的方法，模態分析又稱為自由振動分析，模態分析是一種處理過程，是根據結構的固有特性，包括頻率、阻尼和模態振型，這些動力學屬性去描述結構的過程，通過模態分析可以確定結構的固有頻率、周期及振型.是結構進行動力分析首要考慮的問題.

模態分析的目的在于求系統的固有頻率和振型.在有限元處理主要步驟大概有：建立模型、施加邊界條件、求解設置、后處理等，模態分析是線性分析，忽略非線性.

對于模態分析，動力平衡方程：

這里[M]是結構總質量矩陣；[C]是阻尼矩陣；[K]是結構總剛度矩陣；{u}是結構位移向量；{R(t)}是強迫力矩陣

2.1 結構模態分析

下面對古城墻模型、土-古城墻模型分別進行的模態分析，確定各個模型的動力特性，并提取前十階模態振型，其固有頻率及固有周期如圖所示：

(1)古城墻自振頻率.

(2)古城墻前六階振型.

第一階振型

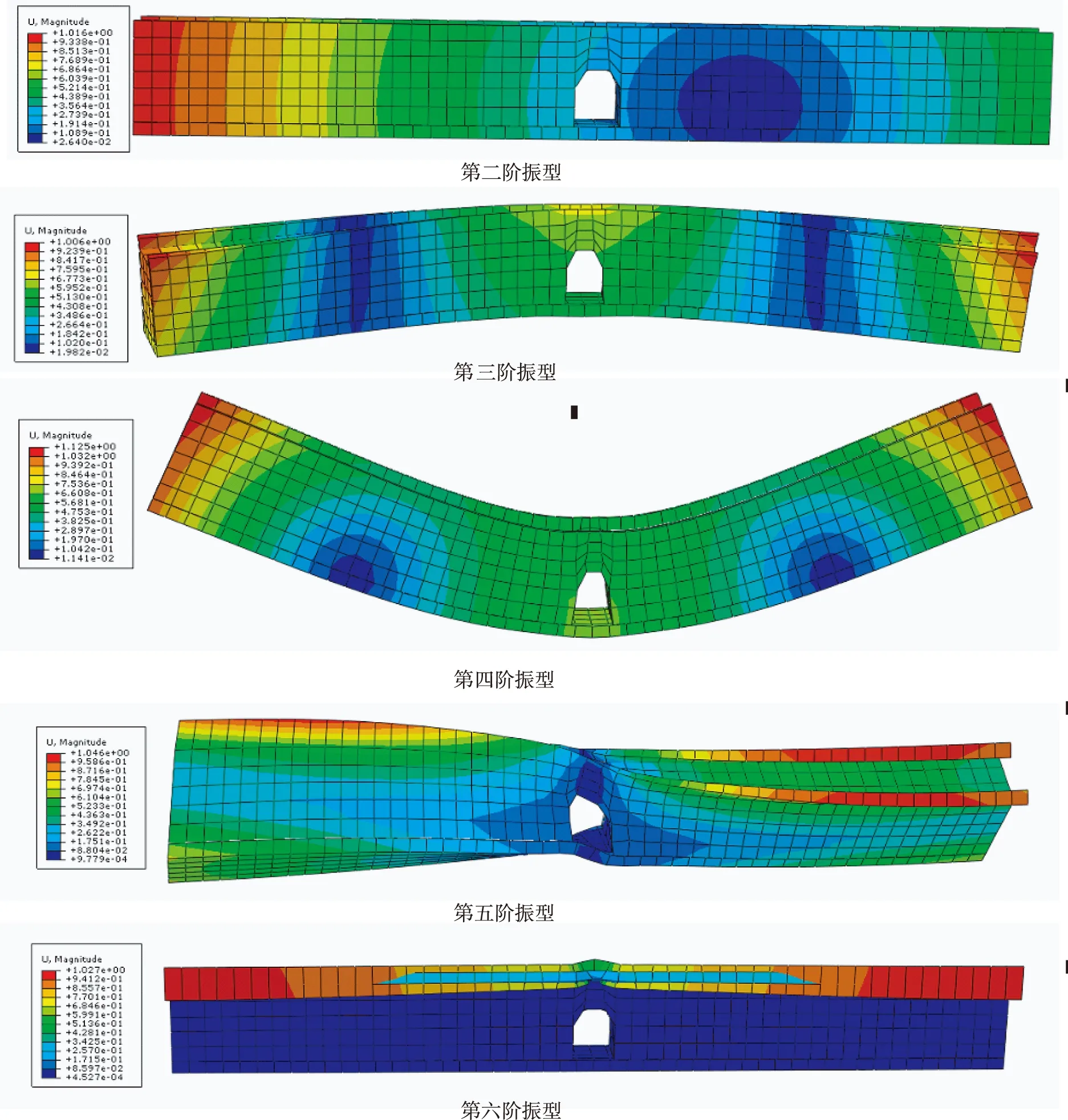
圖2 古城墻結構模型前六階振型

由表5及上列各圖可得，大境門古城墻結構的基本頻率為0.945，基本周期為1.058，結構的第一、二、三階次自振頻率數值相近.前十階振型介于0.945～5.355之間，古城墻結構布置較為規整，一、二階振型主要以沿著X方向平動為主，從第三階振型開始出現了明顯的扭轉特性.各階模態變形最大值均以城墻頂部變形為主，可知城墻頂部在結構固定頻率下容易發生變形.

表5 古城墻模型自振頻率

(3)土-古城墻自振頻率.

(4)土-古城墻前六階振型.

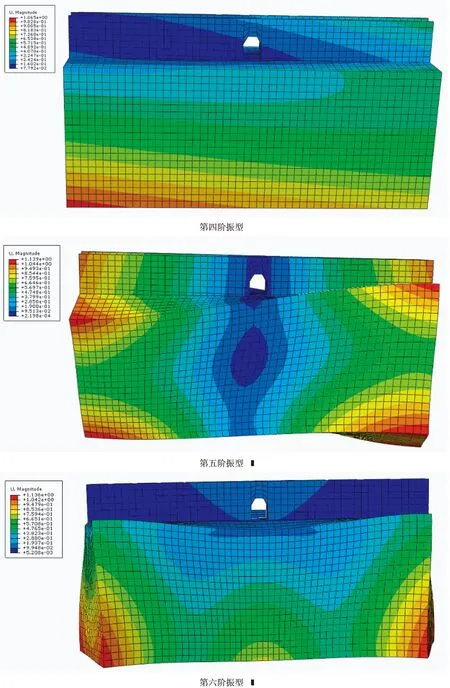
圖3 土-古城墻結構模型前六階振型

由表6及上列各圖可得，土-古城墻結構的基本頻率為0.522，基本周期為1.916，前十階振型介于0.522～1.143之間，第一、二、三階自振頻率數值相近，主要以古城墻模型振動為主，從第四階次開始振動主要是由土層帶動了上部結構共同振動.

表6 土-城墻結構模型自振頻率

2.2 模型模態結果分析對比

將城墻結構模型與土-城墻結構模型的自振頻率繪制成如下圖所示，對比如下：

通過分析圖4可以得出：與古城墻模型相比，土—古城墻模型自振頻率相對于古城墻模型較小，第一、二、三階振型主要表現為古城墻結構模型的振動，第四階開始振型基本上是下部土層和上部古城墻結構共同參與振動，隨著階次的增加，土-古城墻結構自振頻率的增加幅度相比較而言更為平緩，考慮到土與結構共同作用時對結構頻率影響較大，即土層結構存在改變了古城墻結構的自振特性，土-古城墻模型的頻率較小而周期較長，這是由于土層的柔性而使得結構的自振周期延長.

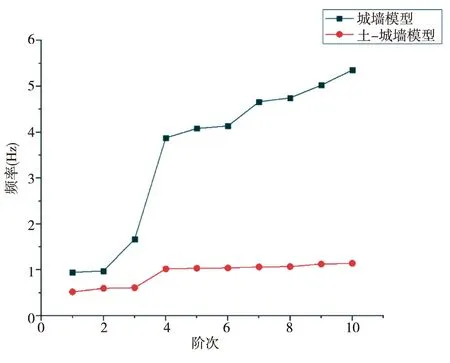
圖4 兩種結構頻率變化對比曲線

3 地震分析

根據《建筑抗震設計規范》GB50011-2010中可以得到，張家口市區的抗震設防烈度為7度，設計基本加速度為0.15 g，設計地震分組為二組，大境門古城墻所在場地為二類場地，本文選取地震波El-Centro波、Taft波及天津波，通過調幅，對模型輸入三種地震波，進行時程分析，輸入節點的加速度和位移時程數據.

3.1 El-Centro波激勵下結構反應

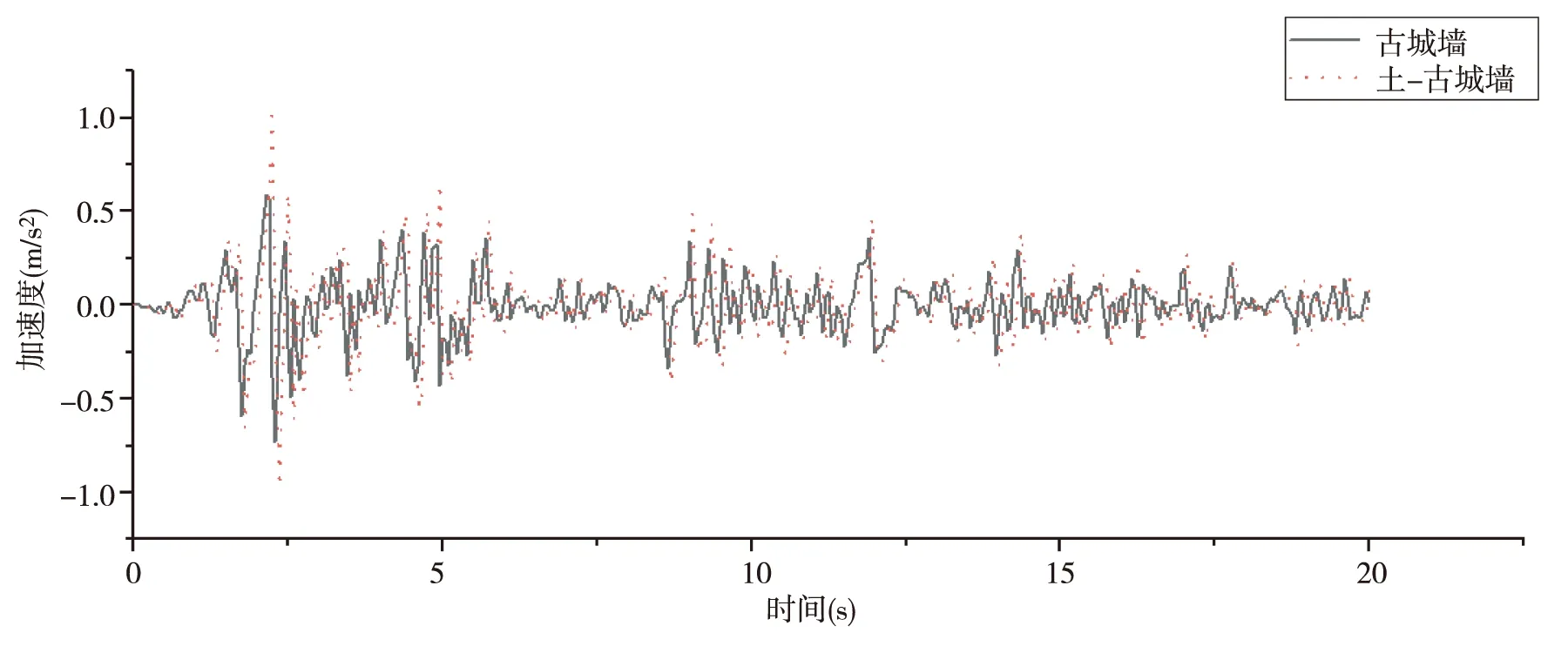
圖6 El-Centro波激勵下頂部節點加速度對比

由圖5、6可以看出，輸入修正后的時間20 s的El-Centro地震波，上部結構古城墻頂部最大位移為10 mm，其發生的時刻為2.65 s，最大加速度值為0.73 m/s2，其發生的時刻為2.3 s，土-古城墻整體結構城墻頂部最大位移為12 mm，其發生的時刻為2.75 s，最大加速度值為1.02 m/s2，其發生的時刻為2.25 s.

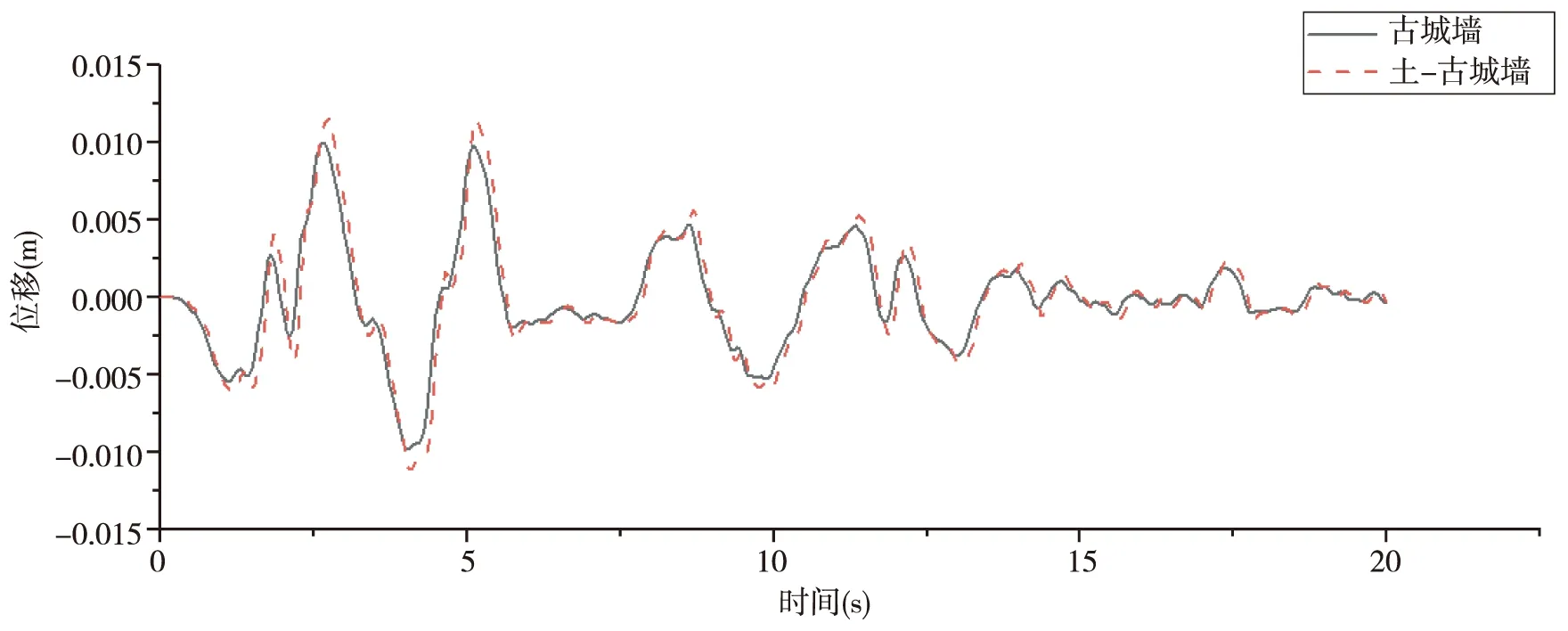
圖5 El-Centro波激勵下頂部節點位移對比

3.2 Taft波激勵下結構反應

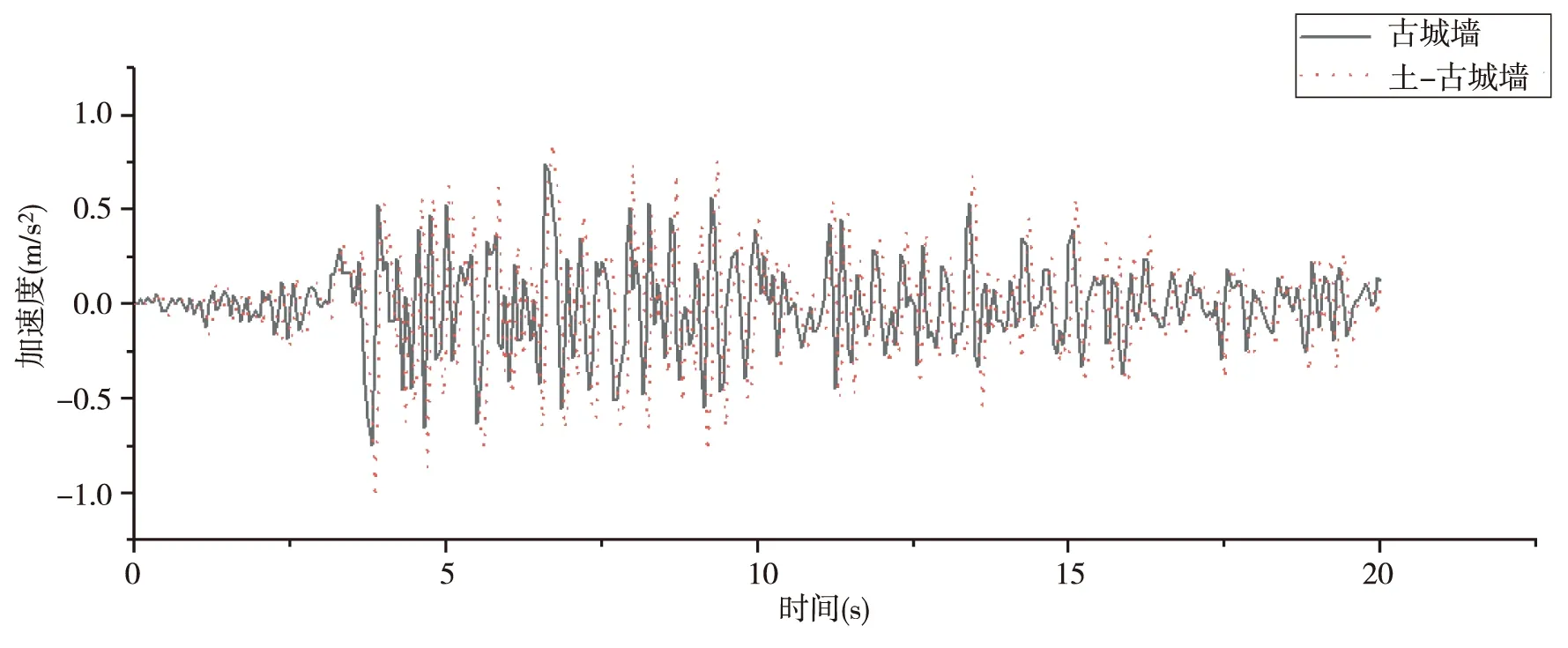
圖8 Taft波激勵下頂部節點加速度對比

由圖7、8可以看出，輸入修正后的時間20 s的Taft地震波，上部結構古城墻頂部最大位移為14 mm，其發生的時刻為6.65 s，最大加速度值為0.75 m/s2，其發生的時刻為3.8 s，土-古城墻整體結構城墻頂部最大位移為17 mm，其發生的時刻為6.7 s，最大加速度值為1.03 m/s2，其發生的時刻為3.85 s.

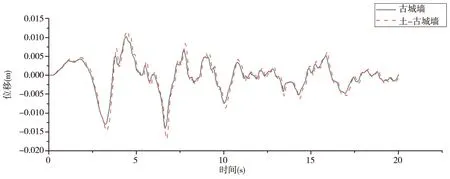
圖7 Taft波激勵下頂部節點位移對比

3.3 天津波激勵下結構反應

由圖9、10可以看出，輸入修正后的時間20 s的天津地震波，上部結構古城墻頂部最大位移為34 mm，其發生的時刻為7.65 s，最大加速度值為0.91 m/s2，其發生的時刻為7.65 s，土-古城墻整體結構城墻頂部最大位移為40 mm，其發生的時刻為7.7 s，最大加速度值為1.01 m/s2，其發生的時刻為7.7 s.

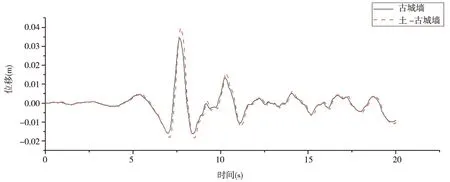
圖9 天津波激勵下頂部節點位移對比

由表7和5-10圖可知，通過數據對比可以得出，存在土層作用時，古城墻模型的位移和加速度反應同時被放大，El-Centro波作用時，整體結構土-古城墻頂部位移是上部結構古城墻模型頂部位移的1.2倍，整體結構土-古城墻頂部動力系數是上部結構古城墻模型頂部動力系數的1.39倍，Taft波作用時，整體結構土-古城墻頂部位移是上部結構古城墻模型頂部位移的1.21倍，整體結構土-古城墻頂部動力系數是上部結構古城墻模型頂部動力系數的1.38倍，天津波作用時，整體結構土-古城墻頂部位移是上部結構古城墻模型頂部位移的1.17倍，整體結構土-古城墻頂部動力系數是上部結構古城墻模型頂部動力系數的1.15倍.

表7 三種地震激勵下模型位移和加速度峰值

4 結 論

通過對古城墻和土-古城墻建立兩種模型，用有限元進行結構動力特性分析，輸入三種地震波激勵，得出兩種模型的位移和加速度，進行比較研究，得出以下結論：

(1)通過模態分析，分別得到古城墻和土—古城墻兩種模型的自振頻率和周期，兩種模型前三階振型較為接近，主要是以上部結構振動為主，但是從總體趨勢可以看出，土層的存在改變了上部結構的自振特性，主要是下部土層帶動上部城墻共同振動，頻率減小，周期變大.

(2)在El-Centro波、Taft波、天津波的激勵下，分別得到古城墻和土—古城墻兩種模型頂部節點的位移和加速度時程，通過比較得以得出，土—古城墻模型的頂部節點位移和加速度均比古城墻模型增大，所以在進行古城墻抗震性能分析的同時，考慮結構與下部土層的相互作用才能使得結構地震時更加安全.