中立切換系統在異步切換下的指數穩定性
齊齊哈爾大學 李明俠
切換系統是眾多系統中特殊的一種動態系統,它是由有限個離散的或者連續的子系統和一個切換信號組成。這個切換信號是用來組織和協調這些子系統進行有序的切換。近幾十年,切換系統在控制論中的應用越來越廣泛[1-6]。時滯是切換系統中較常見的現象,因此在研究切換系統的穩定性問題時要將時滯考慮在內。
在現有的時滯系統穩定性條件中,根據是否依賴系統中時滯的大小,可以將穩定性條件分為時滯獨立和時滯依賴兩類[6]。其中時滯依賴穩定性條件具有更小的保守性。已有的文獻中只規定了一個上界,但是這種規定在工程中不一定成立。在實際工程應用中,時滯可能會更大地超過這個上界,我們稱之為大時滯。而較大時滯在系統中的出現往往導致系統不穩定,因此研究含有大時滯子系統的穩定性是非常必要的[7]。
另外,外部擾動也是減少建模與實際系統的誤差的又一必要的因素。簡言之,在切換系統的研究中,可以利用時滯和擾動來控制系統,可以提高系統的控制效率,進而降低保守性。文獻[5]研究了一類中立切換系統的指數穩定性。異步控制指的是各個控制器間的切換滯后于系統模型,其主要原因是在實際操作中,控制器需要一定的時間去識別系統模型,進而產生了異步。
到目前為止,對于切換系統異步切換下鎮定問題已經被廣泛研究,但是對于含有大時變時滯的切換系統在異步切換下的研究還不夠深入。文獻[1]對于線性切換系統在異步切換下的穩定性問題進行了分析;文獻[4]討論了在異步切換下具有混合時滯的切換系統指數穩定性。基于上述現實,帶有非線性擾動的時滯切換系統在異步切換下的指數穩定性受到越來越多的關注。
對于帶有非線性擾動的時滯切換系統的穩定性分析雖然已經取得了一些成果,但是還不夠深入和完善。因此,在此類系統的穩定性研究方面還需要更多的努力,才能更好的服務社會。本文通過構造李雅普諾夫克拉索夫斯基函數,運用Jessen不等式和平均駐留時間方法,以線性矩陣不等式的形式,分別給出了大時滯系統在控制器匹配和不匹配的情況下系統指數穩定的充分條件。
1 問題描述
考慮如下非線性中立切換系統:
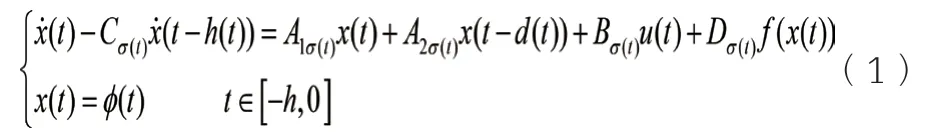
其中,x(t)∈Rn是狀態向量;u(t)∈Rn是控制輸入;A1i、A2i、Ci、Di是已知的適當維數矩陣;σ(t):0,∞→M={1,2,…,l}為切換信號;時變時滯d(t)和h(t)滿足下式:0≤d1 構造一個無記憶狀態反饋控制器式(2):u(t)=Kσ′(t)x(t),這里,{(t0,σ(t0)),(t1+Δ1,σ(t1)),…,(tk+Δk,σ(tk)),…}延遲時間Δk≤Γ。由式(2)閉環式(1)系統簡化為:0≤h1≤h(t)≤h2<∞, 引理1:對于正定對稱矩陣M∈Rn×n和常量γ>0,如果存在一個向量函ω:[0,r]→Rn,則下列不等式成立:。 對于給定常數α>0,β>0,i,j∈M,i≠j,如果存在正定對稱矩陣Pi,R1i,R2i,Q1i,Q2i滿足下式: 這里: 則異步切換下系統指數穩定。 t∈[tk-1+Δk-1,tk)和t∈[tk,tk+Δk)的情形。 2.2.1 當t∈[tk-1+Δk-1,tk)時,構造lyapunov函數 在此區間內,σ′(t)=σ(t)=i,對V1i(t)求導并結合0≤d1 由引理1得: 2.2.2 當t∈[tk,tk+Δk)時,構造lyapunov函數 在此區間內,σ′(t)=σ(t)=j,對V1i(t)求導并結合0≤d1 由引理1得: 同理,當t∈[tk+Δk,tk+1)時,我們有: 這里: 因此: 系統(1)指數穩定。 近些年切換系統仍然備受關注,而穩定性作為系統的一個重要特性,仍是系統研究的一個熱點問題。由于時代的發展和科技的進步,系統模型的復雜程度日益增高,對所研究問題的精確程度也越來越高。控制器在系統的穩定性研究中起著非常重要的作用,而子系統與控制器的匹配要花費一定的時間,因此控制器之間的切換往往滯后于子系統之間的切換,進而引發異步切換問題。到目前為止,切換系統的鎮定問題已經得到了廣泛的研究。 本文研究了一類非線性中立切換系統在異步切換下的指數穩定性,通過選取適當的李雅普諾夫—克拉索夫斯基函數,運用平均駐留時間方法和積分不等式,在已有文獻的基礎上得到了更為復雜的非線性中立切換系統在異步切換下系統指數穩定的條件。 切換系統依然有許多問題函待解決,本文所討論的對于含有非線性擾動的時滯切換系統的研究只是初步的,還有許多問題需要進一步研究:離散的非線性時滯切換系統的相關問題。本文所研究的系統是連續的切換系統,未對離散的切換系統加以討論。日后會對離散的非線性切換系統的穩定性問題加以分析;理論聯系實際。由于切換系統的穩定性問題與實際問題的聯系非常緊密,若此類問題的研究僅限于理論的研究是遠遠不夠的,如何將切換系統的穩定性理論應用于實際問題并將所研究理論服務于實際問題是今后值得深入研究的;在今后的研究中會在理論的基礎上加入仿真,以更清晰地說明文章的結論的正確性。
2 主要結果
2.1定理1


2.2證明

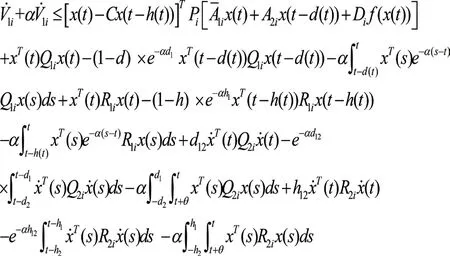




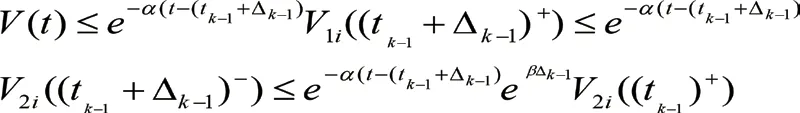




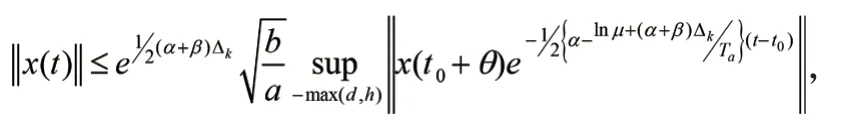
3 結語

