振動式土壤切削系統的振動頻率范圍研究*

張印，郭志軍，田晨樂，龐靖，張盼港，邱毅清

(1. 河南科技大學車輛與交通工程學院，河南洛陽，471003; 2. 河南科技大學農業裝備工程學院，河南洛陽，471003)

0 引言

采用振動方式在特定工況下可以有效減小土壤切削阻力[1-2]，目前主要有強迫振動[3-4]和自激振動[5-6]兩種形式。強迫振動主要通過對土壤切削機具加裝額外激振裝置來實現[7]，在特定頻率、振幅、土壤條件和工作方式下可取得良好減阻效果[8-10]。這種方式可以起到明顯的減阻效果，但是機具和土壤參數一旦不協調，極易出現系統總功耗增加的情況[11-12]。自激振動是在非均勻土壤阻力作用下，利用切削部件自身彈性，使切削部件—土壤相互作用系統產生振動[13]，起到迅速松碎土壤和減阻效果[14-15]。自激振動應用較成熟的有彈齒和切削工具鉸支再附加彈簧[16]兩種，也都存在機具振動參數與復雜土壤條件相互適應問題[17]。無論是哪種振動形式，拓寬機具本身振動參數與土壤固有振動參數彼此之間的匹配和適應能力成為亟待解決的問題。

在頻率、阻尼比和振幅等振動參數中，頻率參數是首要因素，它決定了振動式土壤切削的性質和減阻效果。查閱大量振動式土壤切削機具通過土槽[18-19]或田間耕作[20-21]測試研究成果，發現已采用的機具振蕩頻率分布范圍非常廣，從2 Hz到50 Hz都有采用，并聲稱都取得了較好的減振效果。這對形成相關振動式土壤切削機具參數設計指導性意見就顯得比較困難。

振動式土壤切削機具工作過程中，機具與被切削土壤之間振動參數的合理匹配是有效減阻的關鍵。工程結構在發生共振現象時極易破壞。故本文引入共振理論來探索振動式土壤切削機具振動參數，特別是振動頻率的選取原則。即當機具沖擊振蕩頻率與土壤固有振動頻率比較接近而使被切削土壤發生共振現象時，具有散體材料特征的土壤更易破碎，從而為獲得極低土壤切削阻力創造物理條件。

在測得室內土槽土壤固有振動參數基礎上，以單自由度土壤振動切削模型共振效應分析為基礎，分別使用經驗值、半功率帶寬、振幅放大因子和正態分布等四種方法對土壤第一階固有振動共振頻帶寬度和振動能量占比進行計算和分析，以期為強迫和自激等各類振動式土壤切削機具振動參數設計，特別是振動頻率選擇，以及相關產品開發提供參考。

1 單自由度土壤振動切削模型

在圖1(a)所示切削部件—土壤二維切削模型中，取切削前進方向，即水平+x方向為例，可建立圖1(b)所示土壤單自由度振動模型。

(a) 實際模型

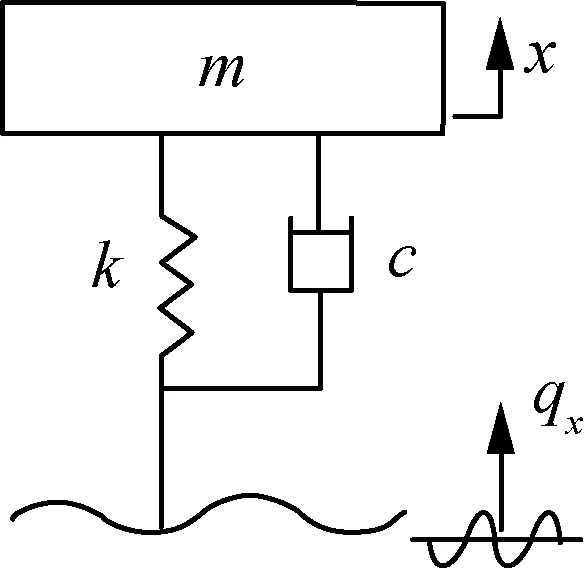
(b) 簡化模型圖1 單自由度土壤振動切削模型Fig. 1 Single freedom soil vibration cutting model

根據牛頓第二定律，可得圖1(b)系統運動微分方程

(1)

代入式(1)有

B(-mω2+ωjc+k)=a(jωc+k)

(2)

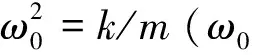
(3)

與放大因子形式相同的幅頻特性方程[23]

(4)

相頻特性方程[22]

(5)

以阻尼比ζ=0.1為例，此系統的幅頻和相頻特性曲線分別如圖2(a)和圖2(b)所示。當觸土部件沖擊頻率等于土壤固有振動頻率，即圖2中系統頻率比λ接近于1時，系統幅頻特性取得極大值點，即系統共振點。或者說，當頻率比λ接近于1時，觸土曲面前方土壤產生共振現象，土壤容易破碎，從而可能獲得較低土壤切削阻力。

(a) 幅頻特性

(b) 相頻特性圖2 單質量系統幅頻和相頻特性Fig. 2 Amplitude-frequency and phase-frequencycharacteristics of single-mass system model

2 土壤固有振動參數測試

測試了室內土槽土壤的固有振動參數。圖3所示土槽內輪廓尺寸為1.5 m×0.8 m×0.5 m。經全面松碎、打勻、刮平和壓實后的有效土體尺寸為1.5 m×0.8 m×0.35 m，體積密度1 394.38 kg/m3、烘干法土壤含水量均值12.45%。

圖3 試驗現場Fig. 3 Test site1. 加速度傳感器及測點布置 2.土槽 3.土壤4.DH5902數據采集分析系統 5.DHMA模態分析系統 6.激振錘

室內土槽設計的目的是為了完成各種鏟刀切土試驗。為了說明問題，結合鏟刀切削工況，對土槽土壤依照右手螺旋定則建立三維坐標系。圖3所示土槽土體上表面縱向中心線與右端面鋼板交點為坐標原點，該平面為xOy平面。圖4給出了該土體上表面俯視圖，鏟刀切削前進方向為+x方向(圖3土槽指向左側)，垂直于土體表面向上為+z方向，左側為+y方向。

圖4 測點與激勵點位置示意圖Fig. 4 Schematic diagram of response points andexcitation point position

土槽土壤固有振動參數可通過頻率響應函數或自由衰減振動測試得到。具體采用錘擊式脈沖激勵—自由衰減振動法完成了相關土壤振動參數測試工作。激振錘的激振位置位于圖3土槽右端面。該點距離土壤上表面0.1 m，激振方向為+x方向，具體激勵點坐標位置為(0，0，-0.1)，參見圖4。選取這個激振點位置和方向是綜合考慮了土槽試驗時模型鏟刀工作深度和前進方向。土壤振動響應通過壓電式加速度傳感器測得。試驗時，將各傳感器埋入土壤表層，傳感器自身高度為16 mm，其上表面與土壤表面齊平。傳感器布置位置主要考慮了鏟刀尺寸、工作方向以及信號響應強弱[24]。全部試驗的測點分布是由78個100 mm×100 mm 的網格組成，共計98個測點，經測試發現沿縱向中心線即切削前進方向的響應依次減弱，靠近圖3土槽右端的測點響應較強。限于篇幅選取其中代表性的五個測點進行闡述，見圖3和圖4。1～5號各測點傳感器在x-y平面的具體位置坐標為(0.3，0.2)、(0.3，0)、(0.3，-0.2)、(0.7，0)和(1.1，0)。各加速度傳感器對振動信號接收方向均為x方向。

(6)

式中：δ(t)——單位脈沖函數。

試驗時由加速度傳感器獲得的振動信號輸入東華測試DH5902數據采集分析儀，經動態分析軟件獲得各振動信號的時間歷程、自功率譜、相干函數圖等。信號傳輸路徑如圖5，儀器設備連接照片見圖3。

圖5 信號傳輸路徑Fig. 5 Signal transmission path

經多次重復試驗，試驗結果比較接近。五個測點加速度信號的代表性時間歷程、自功率譜、相干函數曲線如圖6～圖10所示。

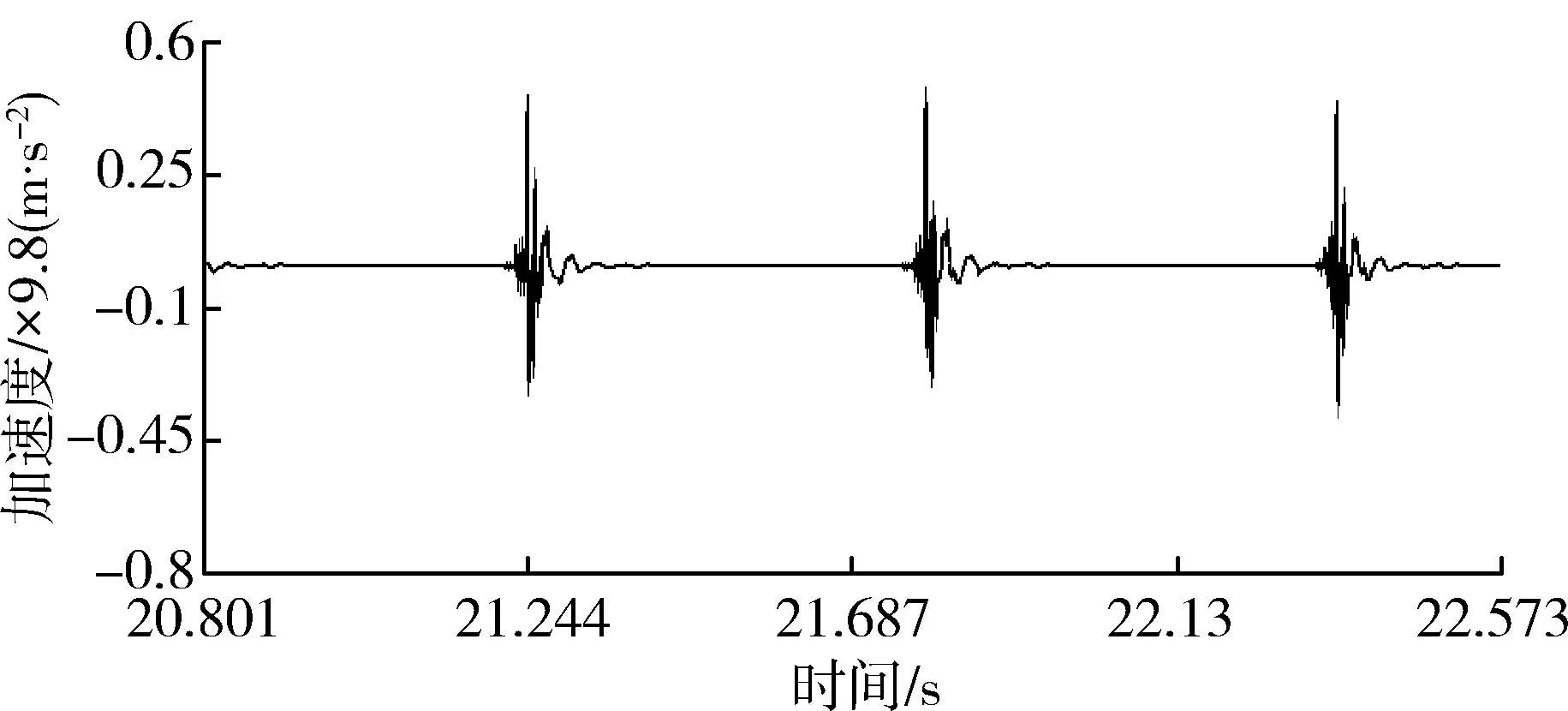
(a) 加速度信號時域圖

(b) 自功率譜

(c) 相干函數圖6 測點1測試結果Fig. 6 Test results of point 1

本次試驗五個測點x方向第一階固有振動頻率依次為29.297 Hz、29.297 Hz、27.344 Hz、31.25 Hz、31.25 Hz，均值為29.688 Hz，標準差為1.461。其中響應測點1、2、3距離激勵位置較近，因此其振幅信號也較清晰，這三個點第一階振動頻率處對應相干函數值分別為0.981、0.983、0.964，振動特征明顯。而測點4和測點5距離激勵點的位置越來越遠，雖然30 Hz振動頻率附近相干函數值也較高，但測得的振幅信號越來越弱。這與實際土壤振動衰減情況是相符合的。因此，僅選取測點1、2、3具有較強振動信號的測試結果展開深入研究。因各測點的第二階振動頻率處振動幅度相對較弱，相干函數值較小，頻率范圍約為70～110 Hz，峰值點不夠清晰，也不易被通常比較低的土壤切削速度激發，故僅對第一階振動頻率作進一步的計算和分析。

(a) 加速度信號時域圖

(b) 自功率譜

(c) 相干函數圖7 測點2測試結果Fig. 7 Test results of point 2

(a) 加速度信號時域圖

(b) 自功率譜

(c) 相干函數圖8 測點3測試結果Fig. 8 Test results of point 3

(a) 加速度信號時域圖

(b) 自功率譜

(c) 相干函數圖9 測點4測試結果Fig. 9 Test results of point 4

(a) 加速度信號時域圖

(b) 自功率譜

(c) 相干函數圖10 測點5測試結果Fig. 10 Test results of point 5

3 土壤共振區寬度與共振能量

為使切削機具工作時產生較好的土壤振動切削減阻效果，一方面，當土壤參數或固有振動頻率固定，需要確定切削工具的振蕩頻率選擇或變化范圍；另一方面，當機具振動頻率固定，需要確定土壤自身參數或固有振動頻率寬度的允許變化范圍。解決這兩個問題的前提是需要探究土壤這種特殊材料的共振區寬度，此處用經驗值、半功率帶寬、振幅放大因子和正態分布等四種方法展開分析。

功率譜曲線所覆蓋的面積在數值上與系統總功率(能量)成正比，故將其積分面積視為振動過程中能量消耗。對于圖6(b)所示測點1的自功率譜曲線第一階共振點附近各坐標點Matlab軟件進行曲線擬合，見圖11。圖中黑色散點為掃描所得圖像的散點圖，細實線為擬合曲線。

圖11 測點1第一階振動曲線擬合結果Fig. 11 First order vibration curve fitting result ofmeasurement point 1

由高斯逼近方法得到的擬合曲線

(7)

3.1 經驗法

3.2 半功率帶寬法

另外，振動系統的阻尼比可由半功率點的頻率差與2倍固有頻率的比值近似得到[28]

ζ=(f2-f1)/2f0

(8)

利用圖6(b)、圖7(b)和圖8(b)三個測點的自功率譜第一階振動頻率處的數據可計算三個測點的第一階固有振動阻尼比分別為0.138、0.137、0.152，均值為0.142，均方差為0.006 8。

3.3 振幅放大因子法

3.4 正態分布法

因正態分布曲線形狀與圖11中曲線形狀有相似之處，為探求共振區范圍，故引入正態分布概念對共振區寬度和振動能量進行計算研究。在正態分布中，隨機變量X服從一個位置參數為μ、尺度參數為σ的概率分布，其概率密度函數如式(9)，記作X～N(μ，σ2)。

(9)

為了使正態分布曲線與圖11形狀相近，將頻率作為樣本值，測得的自功率譜密度值作為頻次，經計算，當μ=f0=29.297 Hz時，可得σ=7.768。

常用的正態分布區間有1σ、2σ、3σ，分別占總面積68.26%、95.44%、99.74%。參考此區間選擇方法，在土壤固有頻率f0=29.297 Hz左右加減1σ、2σ、3σ來選擇共振頻率范圍。由此計算出測點1第一階固有振動共振區頻率范圍和共振能量占比如下。

測點2、3第一階固有振動頻率處共振區寬度和共振能量計算過程與測點1一致，限于篇幅，將此略去，結果見圖12(b)、圖12(c)和表1。

放大因子等于3和半功率帶寬法較接近，相應共振區內土壤振動對于機具振動輸入的放大超過3倍。雖然放大倍數大，但共振區振動能量占比較低。這種共振區劃分對金屬等成分均勻且彈塑性較強材料的共振分析較適合，而對土壤這種成分不均勻、且散體特征明顯的材料來說顯得不是特別必要。雖然放大倍數偏大，有利于碎土，但存在共振區過窄難以適應復雜多變的土壤條件的不足。放大因子等于2(0.717×f0～1.207×f0)、正態分布1σ(0.735×f0～1.265×f0)以及經驗法(0.75×f0～1.25×f0)結果比較接近，這三種方法確定的共振區將振動輸入信號的幅值放大約超過2倍，共振區所占振動能量約為75%，寬度比較適中。因此這三種方法確定的共振區，對于大部分工程振動的共振分析和設計是合適的。而對于振動式土壤切削機具設計而言，仍可拓展更寬的共振區間以增加對復雜多變土壤條件的適應能力。

(a) 測點1

(b) 測點2

(c) 測點3圖12 四種方法計算的共振頻率范圍Fig. 12 Resonant frequencies range calculated by the four methods

表1 各測點共振區振動參數Tab. 1 Vibration parameters of the resonance zone of each measuring point

4 結論

1) 對室內土槽土壤第一階固有振動頻率測試結果為27.344～31.25 Hz，均值29.688 Hz，標準差1.461。

2) 由半功率帶寬法求得室內土槽土壤第一階振動系統阻尼比范圍為0.137～0.152，均值為0.142，標準差為0.006 8。

3) 可采用經驗法、放大因子等于2和正態分布1σ所確定的共振區間作為機具振蕩頻率或系統激勵頻率的選擇范圍(約為0.75f0～1.25f0)。這三種方法的結果比較接近，振動參數的大小比較適中。對于土壤類非均勻且散體特征明顯的材料振動參數設計而言，仍偏嚴，對于復雜多變的土壤條件適應能力有限。

4) 采用振幅放大因子等于1確定土壤共振區(0～1.414f0)來設計系統激振頻率，在較寬頻帶范圍內可保障系統輸入土壤的振動能量不衰減，但某些頻率處的振動切削減阻效果可能略弱。

5) 推薦用正態分布2σ(下限頻率0.470f0)或者正態分布3σ(下限頻率0.205f0)來確定土壤共振區或振動式土壤切削機具的振蕩下限頻率范圍，從理論上即可保證一定的土壤振動強度，又可對復雜多變的土壤條件具有較強適應能力。但這種方法需保證上限截止頻率不得超過1.414f0，或可靠起見，依照正態分布1σ上限頻率1.265f0截止。