無證書的支持樹形訪問結構的屬性基簽名方案

鄧銀娟，杜紅珍，馬巧梅

（1.寶雞文理學院數學與信息科學學院，陜西寶雞 721013；2.寶雞文理學院計算機科學學院，陜西寶雞 721013）

在電子醫療檔案系統中，傳統的數字簽名會造成用戶身份信息泄露，從而給用戶隱私帶來威脅。屬性基數字簽名不僅可以保護簽名者的身份信息，而且可以實現細粒度的訪問結構。2005 年，文獻[1]首次定義了基于屬性的密碼體制，該體制用一組屬性集合定義用戶。文獻[2]中首次提出了屬性簽名ABS(Attribute-Based Signature)的概念，方案的提出是基于屬性加密的，在該方案中訪問結構為單層屬性。屬性簽名在訪問控制方面具有極好的優勢，國內外學者們在其功能性、靈活性以及效率等方面提出了各種改進方案[3-8]。然而，這些屬性簽名所用私鑰一般都由中心化的機構產生，從而會產生安全隱患。在無證書公鑰密碼體制中[9-14]，簽名者的私鑰不完全由中心生成，簽名私鑰由KGC(Key Generate Center)和簽名者共同生成，因此可以有效地解決上述問題。

為了實現安全靈活的訪問控制，文中在分析現有樹形訪問結構屬性簽名的基礎上，利用無證書簽名技術，提出了一種新的無證書的屬性基簽名方案。該方案的創新點有：1）解決了屬性公鑰密碼體系下固有的密鑰托管問題，同時保留其不需要公鑰證書的特性。2）對新設計算法的安全性進行了嚴格的數學證明，并且通過效率分析表明簽名和驗證過程僅使用一次雙線性對運算，計算效率得到很大的提高。最后通過仿真實驗，與效率較高的屬性簽名算法[4]比較，結果表明，該方案具有更好的簽名和驗證效率。

1 預備知識

1.1 雙線性映射

雙線性映射相關定義請參考文獻[5]。

1.2 應用系統架構

電子醫療檔案系統中用戶更新信息的系統架構由4 部分組成：用戶、用戶中心、密鑰生成中心、存儲系統。應用系統架構如圖1 所示。

圖1 應用系統架構圖

具體操作流程如下：

1）系統需要更新某類用戶信息，下發該類用戶的樹形訪問結構給KGC，并通知該類用戶及時將信息上傳到存儲系統更新。

2）用戶選擇自己的簽名公私鑰對和傳輸公私鑰對，并將傳輸公鑰給KGC，申請用戶的部分私鑰，并驗證公鑰。

3）KGC 傳輸加密后的部分私鑰給用戶。

4）用戶對自己要更新的信息進行簽名，并將簽名、要更新的信息以及用戶屬性集合發送給用戶中心。

5）用戶中心驗證用戶屬性集合的邏輯合理性，并將簽名、待更新的信息以及用戶屬性集合發送給存儲系統。

6）存儲系統驗證簽名，若簽名驗證通過，則更新用戶信息。

1.3 秘密共享方法

秘密共享方法請參考文獻[15]。

Case1:當τ為關系“or”時，令τ的每個子結點的值為s；

Case2:當τ為關系“and”時，τ的子結點數量為u，前u-1 個子結點為隨機值，最后一個子結點為

Case3:當τ為關系“threshold”時，如果結點門限值為h，那么隨機選擇一個h-1次的多項式f(x)，使得f(0)=s；索引次序為的子結點，取值為f(i)。

從根結點起，由上述法則為每個結點自頂向下、遞歸地賦值，最后完成所有葉結點的賦值。

1.4 秘密重組算法

由秘密共享辦法定義一個與其可逆的遞歸算法Verify(Node)，該算法對象Node是樹形訪問結構的各個結點，分情況處理如下[16]：

Case1：當Node結點不是葉結點，關系為“and”時，遍歷此結點的所有子結點，并將所有子結點的返回值作乘積，結果為該結點算法的返回值；若存在一個子結點不滿足要求，則返回驗證失敗；

Case2：當Node結點是非葉結點，關系是“or”時，遍歷此結點的所有子結點，當遇到首個滿足條件的子結點時，遍歷停止，并且返回該子結點的值，即為此結點的驗證值；若所有子結點都不滿足要求，則返回驗證失敗；

Case3：當Node結點是非葉結點，關系為“threshold”，且門限值為h時，遍歷此結點的所有子結點。當子結點中滿足要求的個數大于或等于h時，選取其中h個結點，記集合為H，計算的值并返回；當子結點中滿足要求的個數小于h時，返回驗證失敗。

Case4：當Node結點是葉結點，且葉結點的屬性值滿足i∈w時，返回σi，當i?w時，返回⊥。

1.5 拉格朗日插值

定義1（拉格朗日插值）設f(x)是值域Zp上的一個h-1 次多項式，設元素個數為h的集合為S?Zp，那么可以通過下面公式求得f(x)：

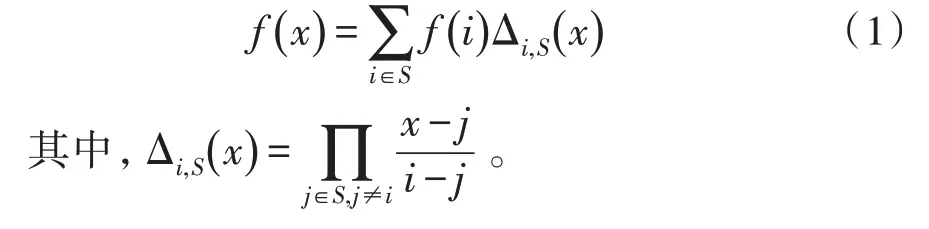
2 算法描述

1）系統建立階段

setup(λ):輸入安全參數λ，選取一個階為q(q為大素數，且q>2λ）的加法群G1和乘法群G2，設g為G1的生成元。e:G1×G1→G2是一個雙線性映射，H:{0,1}?→為抗碰撞哈希函數，設屬性集合為U={1,2,...,n} 。隨機選取，并定義樹形訪問結構為T。參數定義如下：

params={g,G1,G2,e,H}，MSK=y。

2）密鑰值建立階段

Set-Secret-Value(params):用戶隨機選取s,SKs=s為用戶傳輸私鑰，SKx=x為用戶簽名私鑰，計算公鑰PKs=gs,PKx=gx。

3）部分私鑰提取階段

Extract-partial-private-key(params,w,MSK,PKs,T):w為用戶屬性，MSK為系統主密鑰，PKs為用戶的傳輸公鑰，MSK為共享秘密，由秘密共享方法將其賦值給樹形訪問結構的所有結點。設葉結點的屬性集合為L，葉結點的賦值為{yi,i∈L}，隨機選取，則定義集合S={si,1 ≤i≤n}，其中：

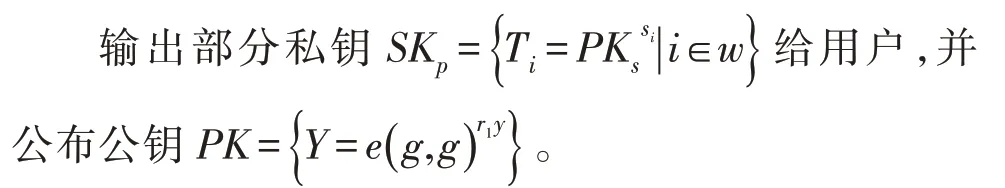
4）私鑰建立階段

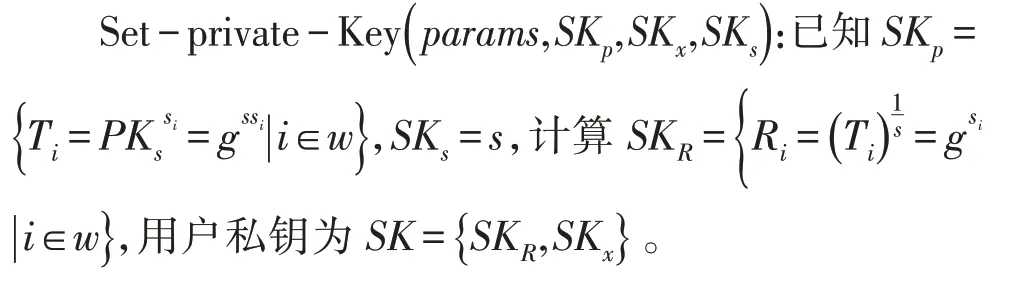
5）簽名階段

6）驗證階段

Verify-Sign(params,T,m,PK,PKx,σ):params為系統參數，樹形訪問結構為T，消息為m，樹形訪問結構根結點為τ，驗證簽名等式如下:

3 安全性分析

3.1 正確性

方案的正確性證明如下。

當Node為樹形訪問結構根結點τ時，。驗證簽名:

3.2 匿名性

定理1：該方案在選擇屬性攻擊下，滿足匿名性。

證明：假設一個多項式時間敵手A模擬簽名者。設C為挑戰者應答A的詢問。模擬交互過程如下：選擇兩個長度相同的屬性集合{w0,w1}，C任選其一進行簽名，則敵手A正確區分簽名及部分私鑰的概率可忽略。

1）系統建立階段：C運行系統生成算法Setup(λ)，生成系統參數params，系統主密鑰MSK={y} 。

2）密鑰值建立階段：敵手A選取隨機數s,x∈，計算PKs=gs,PKx=gx,SKs=s,SKx=x。

3）部分私鑰提取階段：挑戰者C隨機選擇一個比 特b∈{0,1}，并執行算法 Extract-partial-private-key (params,wb,MSK,PKs)以生成部分私鑰，，其中i∈U,為隨機選取的；生成本次簽名的系統公鑰

4）私鑰建立階段：A運行Set-Private-Key(params,SKpb,SKx,SKs)，生成SK={SKR,SKx} 。

5）簽名階段：A運行Sign(params,SK,m)，生成，其中

6）驗證階段：C運行Verify-Sign(params,T,m,PK,PKx,σb)，給出簽名的驗證結果。

7）挑戰階段：敵手已知消息{w0,w1}、部分私鑰SKPb、簽名σb={σ1,σ2} 以及簽名的驗證結果。但簽名過程中僅有部分私鑰SKpb含有屬性信息，而經過r1及ti的隨機化，敵手無法正確區分屬性屬于哪個集合。

綜上所述，敵手A成功輸出b∈{0,1} 的概率為，故方案滿足匿名性。

3.3 不可偽造性

定理2：在標準模型下，提出的無證書屬性基簽名方案滿足不可偽造性。

證明：不失一般性，假設存在攻擊者A1(不知系統主密鑰但可以對用戶的公鑰進行任意的替換)、A2(知道系統的主密鑰不能替換目標用戶的公鑰)，定義攻擊游戲Game1，Game2，在游戲過程中C為挑戰者，模擬挑戰詢問。

1）Game1：模擬攻擊者A1的偽造游戲

系統參數設置：挑戰者C執行系統參數生成算法Setup(λ)，從而生成系統參數params={g,G1,G2,e,H}及主密鑰MSK={y} 。C發送params給攻擊者A1。

①詢問階段

秘密值詢問：A1對用戶i的秘密值進行詢問，C運行算法Set-Secret-Value(params)生成SKxi=xi和SKsi=si。如果用戶i的部分私鑰提取詢問已經被執行，則輸出⊥，否則將SKxi和SKsi發送給用戶A1。

部分私鑰提取詢問：A1對用戶i的部分私鑰進行詢問，C運行 Extract-Partial-Private-key(params,w,MSK,PKsi)生成部分私鑰SKPi=如果已經執行了用戶i的秘密值詢問，則輸出⊥，否則發送SKPi給A1。

簽名詢問：A1對用戶i在消息mj的簽名進行詢問，C運行算法Sign(params,SKi,mj)輸出簽名σi={σ1i,σ2i}，其中

②偽造階段

A1詢問以上信息后，輸出一個簽名者i在消息m?上的有效簽名σ?。簽名需滿足下面兩個保證條件：a.簽名者i未同時提交秘密值詢問和部分私鑰提取詢問；b.沒有對消息m?進行過簽名詢問；

以下分析A1在m?上的簽名σ?的有效性概率，SK={SKR,SKx} 需A1通過詢問獲取，生成簽名的必要條件。SKx可以由秘密值詢問獲取，SKR=，SKp需要經過部分私鑰提取詢問獲得，SKs可以通過秘密值詢問而獲取，SKR及SKx是經過Set-Secret-Value 算法隨機生成的，SKp的隨機性由Extract-Partial-Private-key 算法的ri和ti保證，由條件a 通過計算SK偽造有效簽名的概率可以忽略。在無證書簽名詢問中，r2保證了詢問簽名σi的隨機性，由條件b 通過詢問簽名方式獲取有效簽名的概率可忽略。

因此，Game1 中A1獲取勝利的概率可忽略。

2）Game2:模擬攻擊者A2的偽造游戲

系統參數設置同Game1，C將params和MSK發送給攻擊者A2。

①詢問階段

秘密值詢問：同Game1，C將PKxi和PKsi發送給攻擊者A2；

部分私鑰提取詢問：同Game1，A2可獲取wi，SKpi；

簽名詢問：同Game1；

②偽造階段

A2通過以上詢問，輸出一個簽名者i對消息m?的有效簽名σ?。

簽名滿足保證條件：消息m?未經簽名者i的簽名詢問。

以下分析簽名的有效性：因為A2不能執行公鑰替換，所以A2輸出的簽名驗證必須為合法用戶的公鑰，A2已通過秘密值詢問獲取一系列的用戶有效公鑰值。由于簽名需要相對應的用戶私鑰才能使偽造的簽名驗證通過，而，根據公鑰要求解私鑰xi相當于解離散對數問題，因此，A2偽造成功簽名的概率可忽略，從而贏得Game2 游戲的概率可忽略。

綜上所述，A1贏得Game1 的概率可忽略，A2贏得Game2 的概率可忽略，所以提出的無證書的屬性基簽名方案滿足不可偽造性。

4 效率分析

表1 給出了提出方案與現有效率較高的樹形訪問結構屬性簽名方案在功能上的對比。

表1 方案功能比較

表2 給出了提出方案與現有方案在性能上的對比。ω表示簽名者擁有的屬性個數，|G1|表示G1中元素的長度，|G2|表示G2中元素的長度，l表示訪問結構中所有屬性的個數，m表示消息的長度，S表示訪問結構中用到的所有內結點的集合，內結點集合的元素個數表示為ξ=|S|，h表示為訪問結構中所有“threshold”中門限的和，P和EXP分別表示雙線性對運算和指數運算的時間。

通過表1 和表2 的比較可以看出，提出方案在功能上具有無證書性，可以有效地削弱KGC 的權限，避免密鑰托管問題。在性能上，提出方案比其他兩個方案具有更短的密鑰長度和簽名長度，并且在簽名生成和驗證開銷上花費更短的時間。

表2 方案性能比較

實驗中樹形訪問結構如圖2 所示，為3 層結構，其中“threshold”的門限值為2，簽名者的屬性集合ω={1,2,4,5,7}。圖3 給出了在Inter(R) Core(TM)2 DuoT6670 CPU 2.2GHz 2.00 GB RAM 的計算機上，提出方案與文獻[4]算法的平均運行時間對比，用JPBC 庫在Eclipse 上實現。

圖2 樹形訪問結構示意圖

圖3 算法的平均運行時間對比

5 結論

提出的方案可用于電子醫療檔案系統的用戶信息更新的操作方案，使用無證書的屬性基簽名來保證用戶更新信息的完整性。無證書密碼體制的使用，削弱了密鑰生成中心的權限，解決了傳統的密鑰托管問題。在系統安全性得到提高的情況下，效率也有了很大的提升。