基于自適應門限的改進BigBand算法

龐 健 秦明偉 王 煥 姚遠程

(西南科技大學信息工程學院，特殊環境機器人技術四川省重點實驗室，四川綿陽 621000)

1 引 言

隨著無線通信技術的迅猛發展，可供使用的頻通信段越來越緊缺。同時，授權用戶所分配的頻段資源長時間空閑、非授權用戶可使用的頻段資源稀少。認知無線電技術(Cognitive Radio，CR)可通過高效地分配頻段資源，提高頻譜利用率，解決頻譜資源匱乏問題。

頻譜感知是實現認知無線電的基礎和前提，尤其是GHz寬帶頻譜感知。根據奈奎斯特采樣定理，采集高速率信號要求高采樣率的模數轉換器(Analog Digital Converter，ADC)。目前，由于高速、高性能的ADC工藝復雜、價格昂貴等原因，變得難以獲取。

2006年，D.Donoho等人提出了采樣率遠低于采樣定理的壓縮感知技術(Compressive Sensing，CS)。其最大的特點是隨機采樣、邊采樣邊壓縮，能有效降低認知系統重建信號時所需的采樣率，為認知無線電寬帶頻譜感知技術的實現提供了可行性方案。但在實際運用中，壓縮感知也存在著計算復雜度高、硬件開銷大、實時性難以保證等問題。

2014年，Hassanieh等人提出了BigBand欠采樣算法。該算法的基本原理是利用信號時域時延與信號頻域相位變化的關系，確定混疊頻點的位置和幅值，最終從欠采樣信號中恢復出寬帶頻譜。經理論驗證，在理想條件下，利用兩塊42MHz和兩塊50MHz的ADC可以捕獲1.05GHz的帶寬。但算法中大量的參數來自經驗數據(例如頻譜混疊后的門限閾值)，在低信噪比和噪聲劇烈變化的環境下，頻譜感知性能較差。

基于以上問題，本文針對BigBand算法中的門限問題，通過對環境噪聲和信號的統計分析，提出一種基于自適應門限的改進BigBand算法，該算法主要特點是將噪聲門限、信號門限與預設信號虛警概率及感知環境的信噪比相關聯，并參考歷史判決結果選取門限值，以提高BigBand算法的抗干擾性和檢測性能。

2 BigBand算法

BigBand算法的難點及重點在于解決頻譜混疊問題，主要為混疊頻點頻率和幅度計算。

2.1 頻點分桶

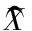
信號的頻域可表示為

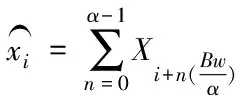
(1)

由式(1)可知，頻點由間隔

α

均勻散列分布到同一個頻率范圍內(稱之為桶)。頻率

f

分布桶的位置為

i

=

f

(

Bw/S

),桶中的值是散列分布到桶中頻點的值之和。

在大多數情況下，檢測的頻譜是稀疏的(頻譜使用率在5%左右)，所以BigBand算法將桶的能量(即幅度平方)與接收器的噪聲進行比較，將能量低于門限值的桶視為空桶并忽略，將焦點放在有信號的桶上。這樣不僅能降低計算復雜度，還能提高頻譜感知速度。

2.2 頻率估計

若在同一個桶中只散列分布了一個大值頻點(信號頻點)，則認為不發生頻譜沖突，此刻桶的頻率值即為該單一大值頻點的值，確定該大值頻點頻率值的過程稱為頻率估計。

在快速傅里葉變換(Fast Fourier Transformation,FFT)中，利用信號時域的偏移與頻域的相位變化的關系，可以估計出頻率

f

。

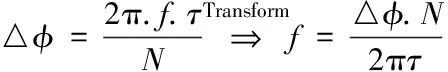
(2)

式中：

τ

——輸入信號采樣的時間偏移量。由于相位周期為2π，為了避免頻率值較大時引起的相位環繞，

τ

的值必須非常小，理論上

τ

的階數應為1

/Bw

。

2.3 頻點沖突檢測與處理2.3.1 頻點沖突檢測

若在同一桶中散列分布了兩個或兩個以上的大值頻點，則認為發生了頻譜沖突。沖突檢測的方法利用FFT的相位旋轉特性，具體如下。

未發生沖突時，即桶中只有一個大值頻點，若延時前后該桶中頻點的值分別用

X

′(

k

)，

X

′()(

k

)表示，則它們的關系可表示為

X

'()(

k

)=

X

′(

k

)

.e

2π=

X

(

f

)

.e

2π

(3)

在延時前后，頻率值會隨延時

τ

的改變而改變，但幅值是不變的，均為

X

(

f

)。當大值頻點

f

和

f

′發生沖突時，延時前桶中的頻點的值

X

′(

k

)為

X

′(

k

)=

X

(

f

)+

X

(

f

')

(4)

延時后該值為

X

'()(

k

)=

X

(

f

)

.e

2π+

X

(

f

′)

.e

2π

(5)

通過比較

X

′(

k

)和

X

′()(

k

)的幅度值是否相等，即可以檢測出信號欠采樣后是否發生了沖突。

2.3.2

頻點沖突處理

互質采樣(根據中國剩余定理)保證了兩個頻率在一次采樣中發生碰撞，在另一次采樣中不會發生碰撞。通過迭代的方法來解決沖突，即混疊頻點的值減去非混疊頻點的值得到混疊前兩個頻點的頻率值。

捕獲頻譜帶寬

Bw

，需要使用到兩個ADC，它們的采樣速率分別為

Bw/α

、

Bw/β

，

α

和

β

和互質。在前述還有一個延時

τ

的采樣，因此BigBand算法分別需要兩種不同采樣率的低速ADC兩個，具體算法流程如圖1所示。

圖1 BigBand算法流程圖Fig.1 Flow chart of BigBand algorithm

3 自適應門限算法

3.1 門限問題分析

在傳統BigBand算法中，對桶的門限設定主要依靠經驗，將高于某一門限值的桶判定為信號桶，其余的桶設定為零。理想情況下，信號值相對于噪聲值是一個相對大值，設置一個較高的門限就可以將噪聲桶全部去掉，保留全部信號桶，最后通過解頻譜混疊恢復出原始寬帶頻譜。

在實際情況中，因為環境中存在噪聲干擾，每一個桶都是有值的，頻譜混疊會使噪聲的值被疊加放大。在復雜的環境下，信號淹沒在噪聲中，信號桶與噪聲桶更是難以區分，一個合理的桶門限閾值至關重要，這個閾值既要能保證所有的信號桶被保留，又要盡可能多的去除噪聲桶。由經驗獲得的門限閾值不適用于這種復雜環境。

3.2 門限算法

針對噪聲不確定性及低信噪比的復雜環境，本文提出基于自適應門限的改進BigBand算法，該算法利用復雜環境的信噪比差異，動態調整桶的門限閾值，使判決門限與信噪比相關聯，提高BigBand算法在復雜噪聲環境下頻譜感知的準確性。

首先，由預設虛警概率獲得初始噪聲桶閾值

λ

和信號桶閾值

λ

，再感知不同信道得到信道信噪比。然后根據信噪比獲得兩個桶閾值的加權因子，并通過加權因子調整門限閾值，最后根據歷史數據選擇新閾值作為門限進行判決與感知。根據信號虛警概率

P

可獲得初始噪聲桶門限

λ

和信號桶門限

λ

可表示為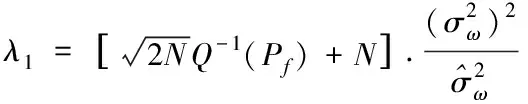

(6)

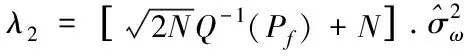
(7)

判決門限的加權因子可表示為

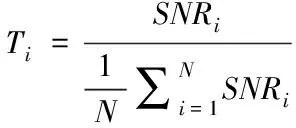
(8)

式中：

T

——門限計算時的加權因子；

SNR

——頻譜感知信道的信噪比；

N

——需要進行門限判決的被檢測桶的數目。

依據加權因子對獲得的初始門限閾值進行調整的計算公式為

λ

_

T

1=

λ

/T

(9)

λ

_

T

2=

λ

/T

(10)

考慮感知信道的歷史使用情況，選擇判決門限。若前一時刻檢測到信號值即主用戶存在(H)，則選擇

λ

_

T

1作為當前檢測的門限值；若前一時刻主用戶不存在(H)，則選擇

λ

_

T

2作為當前的門限值。門限判決方法流程如圖2所示。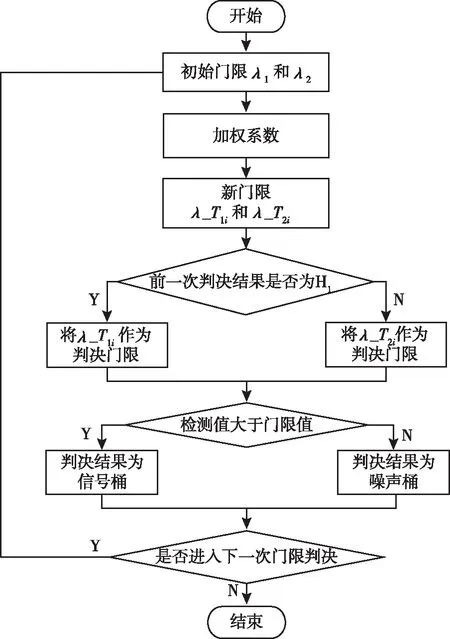

圖2 門限判決方法流程圖Fig.2 Flow chart of threshold judgment method

4 實驗結果與分析

在信噪比為-17dB條件下，基于自適應門限的改進BigBand算法得到的桶門限，如圖3所示。噪聲桶門限可以濾去大部分的噪聲桶，但還是會有部分少量噪聲桶信號大于噪聲門限，此時信號桶門限就可以發揮只保留信號桶作用。

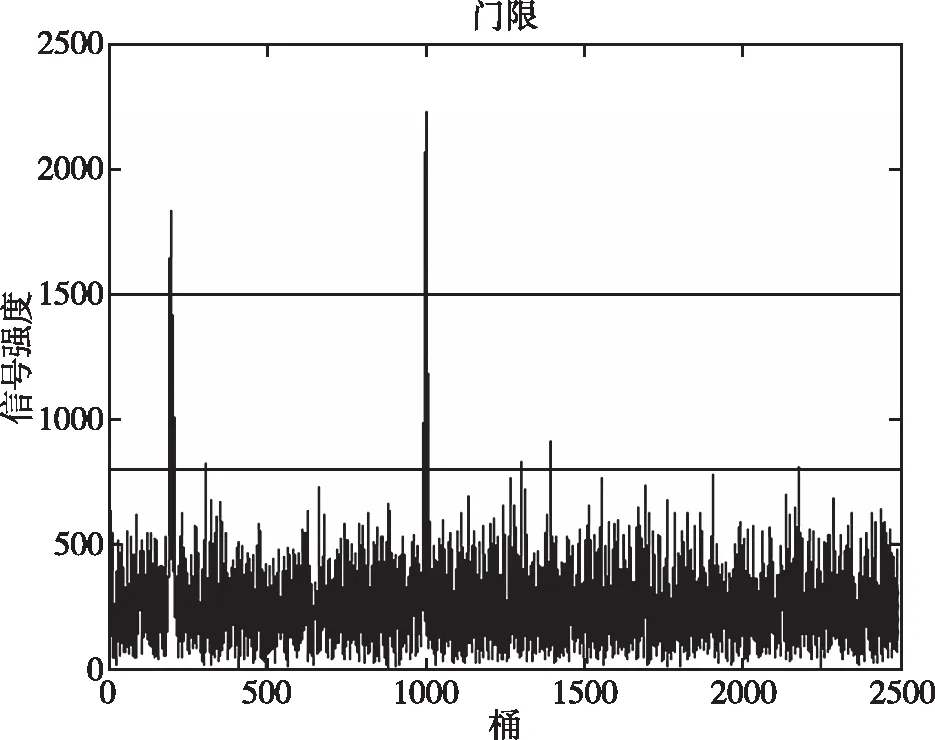
圖3 SNR=-17dB時得到的門限域值波形圖Fig.3 Wave of threshold value obtained when SNR=-17dB

為了進一步證明改進BigBand算法的有效性和感知的準確性，在matlab上對算法進行了驗證。在信號不同的虛警概率條件下，測試改進BigBand算法與傳統BigBand算法的檢測性能，同時與經典的能量檢測性能進行比較；并在不同信噪比條件下測試改進BigBand算法的頻譜感知性能。

在信噪比為-17dB條件下，改進BigBand算法、BigBand傳統算法和傳統的能量檢測算法的信號檢測概率與信號虛警概率變化關系，如圖4所示。從結果中可得，在固定信號虛警概率的條件下，改進BigBand算法的檢測概率明顯高于其他兩種檢測算法，頻譜感知的準確性更好。在信號檢測概率接近1時，改進算法的信號虛警概率明顯低于傳統BigBand算法。

圖4 不同檢測算法性能對比曲線圖Fig.4 Comparison of detection performance based on different detection algorithms

在不同信噪比條件下，改進BigBand算法的信號檢測概率與信號虛警概率變化關系，如圖5所示。從仿真結果中可得，在信噪比條件一定時，檢測性能隨信號虛警概率的增加而變得更好。在信號虛警概率一定時，信噪比越高，信號檢測性能越好即頻譜感知準確性更好。同時，可以注意到，在不同信噪比條件下，信號的檢測概率是趨于一致的，且變化范圍較為接近。可以說明改進BigBand算法可以適應一定復雜程度的噪聲環境。

圖5 不同信噪比環境下檢測性能曲線圖Fig.5 Detection performance curve under different SNR environments

5 結束語

本文針對BigBand算法在復雜噪聲環境中感知性能較差的問題，對BigBand算法進行改進。在其依靠經驗獲取判決門限的基礎上，利用預設信號虛警概率作為條件獲得初始門限閾值，再通過感知信道的信噪比調整門限閾值，并參考信道的歷史感知結果選擇判決門限。MATLAB仿真結果表明，該算法的檢測性能優于傳統的BigBand算法，在低信噪比及噪聲變化劇烈的環境下能考慮到環境噪聲對檢測性能的影響，具有較好的噪聲環境適應性和抗干擾性。能進一步提高BigBand算法頻譜感知的可靠性和準確性。