銫原子Ramsey躍遷仿真模型與實驗研究

閆雨菲 陳海軍 馮進軍

(北京真空電子技術研究所，微波電真空器件國家級重點實驗室，北京 100015)

1 引 言

銫束頻標具有優異的頻率準確度和長期穩定度，在導航、通信和精密測量等領域得到廣泛應用。銫原子在微波互作用系統中發生超精細能級躍遷，其中相鄰

σ

躍遷(

ΔF

=±1,

Δm

=±1)、微波腔兩互作用區相位差以及C場不均勻等因素均會影響銫原子Ramsey躍遷線形，導致銫束頻標產生頻移，影響其頻率準確度和長期穩定運行。銫束頻標自出現以來，許多學者對C場、多普勒效應、頻率牽引效應、伺服電路不完善引起的頻移以及與輻射場有關的頻移分別進行了深入的理論和實驗研究。但實際實驗中往往多種頻移因素融合在一起，導致所測躍遷線形較為復雜，為具體分析每種因素的影響帶來困難。本文綜合考慮相鄰

σ

躍遷、腔相差以及C場不均勻對躍遷線形的影響，建立了一種銫原子Ramsey躍遷仿真模型。該模型可以分別對理想情況和非理想情況下的躍遷線形進行仿真模擬。并且開展了實驗研究，將實驗測得的線形與仿真模擬的線形進行比對，通過多次調節仿真模型中的參數得到與實驗基本一致的仿真線形，從而找出實驗中與理想情況不一致的參量，對實驗過程中的問題修正具有重要的指導作用。

2 銫原子Ramsey躍遷仿真模型

2.1 理論基礎

銫原子基態超精細能級結構如圖1所示，豎直實線為

ΔF

=±1,

Δm

=0的π躍遷，虛線為

ΔF

=±1,

Δm

=±1的

σ

躍遷。基態兩能級之間的超精細能級躍遷由

ΔF

=±1,

Δm

=0的7條π躍遷和

ΔF

=±1,

Δm

=±1的14條

σ

躍遷組成，銫束頻標采用(3,0)-(4,0)的中心π躍遷頻率作為參考頻率。早期，Ramsey發明了用兩個分離振蕩場來激勵躍遷的方法，可以大大壓窄線寬，獲得較窄的譜線，被廣泛應用于銫束頻標中。微波與原子相互作用如圖2所示，假定

F

=3態的原子進入微波腔，這些原子在恒定均勻弱磁場(C場)與相互作用區的微波高頻磁場作用下具有一定激勵時，發生

ΔF

=1,

Δm

=0超精細能級躍遷。到達微波腔出口時，原子能態混雜，這些不同能態的原子從微波腔出口出射。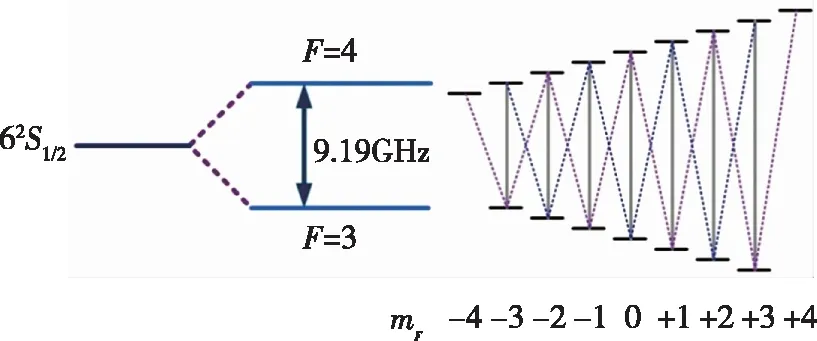

圖1 銫原子基態超精細能級結構圖Fig.1 Superfine level structure of cesium atoms

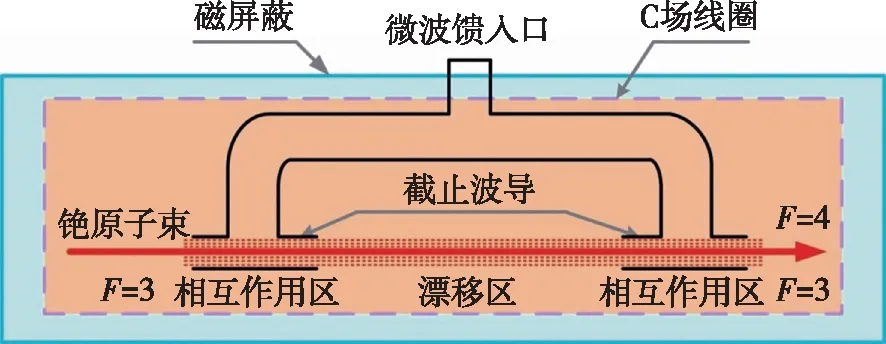
圖2 微波互作用系統結構圖Fig.2 Structure diagram of a microwave interaction system

銫原子在微波腔內發生超精細能級躍遷的幾率為

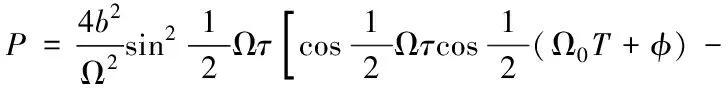
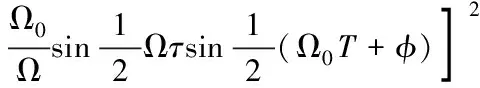
(1)

式中：

τ

——原子在每個相互作用區內運動的時間；

T

——原子在漂移區的運動時間；

φ

——兩個微波互作用區的相位差，即第一個振蕩場的相位比第二個振蕩場超前

φ

式中：

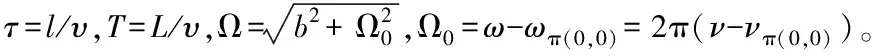
l

,

L

——每個相互作用區和漂移區的長度；

ω

——微波角頻率；

ω

——0-0躍遷線角頻率，

ν

是有磁場擾動時的躍遷頻率。其中，

ω

=2π

ν

，即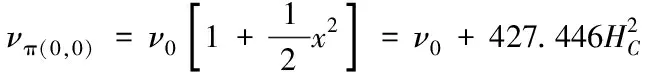

(2)

式中：

ν

——零場躍遷頻率，為9 192 631 770Hz；

μ

——玻爾磁子，

g

,

g

——電子和核的g因子；

ΔW

——兩個基態能級在零磁場時的能量差；

H

——靜磁場強度；

b

——拉比角頻率，在π躍遷和

σ

躍遷時有不同的表示式。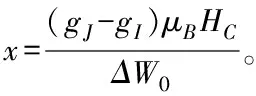

對π躍遷，有

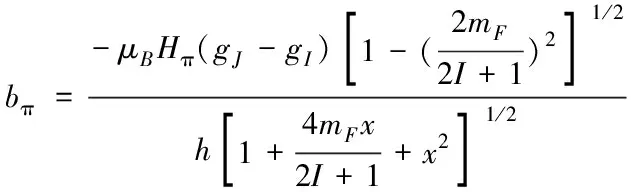
(3)

對

σ

躍遷，有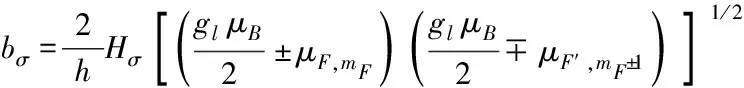

(4)

式中：

H

,

H

——平行及垂直于C場的微波磁場分量；

I

=7

/

2——核自旋數；

μ

,——(

F

,

m

)態的有效磁矩；

μ

′,±1——(

F

′,

m

±1)態的有效磁矩。

表達式如下

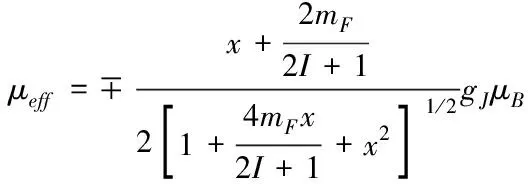
(5)

其中，(3,

m

)態原子取“+”，(4,

m

)態原子取“-”。

通常在最佳微波功率條件下對躍遷幾率展開研究，微波功率對原子躍遷信號強度的影響如圖3所示可以看出，存在一個微波功率使得原子束躍遷信號強度最大，總體呈現不斷衰落的趨勢。本模型中選取使得(3,0)-(4,0)躍遷信號最強時的功率為最佳微波功率。

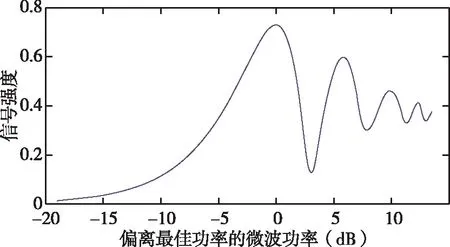
圖3 微波功率與原子束信號強度之間的關系圖Fig.3 Relationship between microwave power and atomic beam signal strength

2.2 仿真模型的建立

2.2.1

原子速率分布

由于束中原子存在速率分布，觀察到的Ramsey躍遷線是對速率取平均的結果，即通過對原子速率分布上的躍遷幾率求平均來計算束中發生躍遷的幾率為

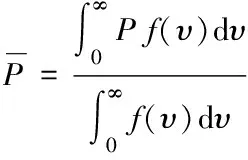
(6)

式中：

f

(

υ

)——束中原子的速率分布，對Ramsey躍遷的線形及線寬有影響。

對于磁選態銫束頻標，探測到的原子速率受選態磁場及束光學的影響較大。此理論模型可將磁選態銫束頻標中實際計算或實驗測試得到的速率分布代入式(6)進行計算。而光抽運銫束頻標中的原子沒有選速作用，其速率分布為

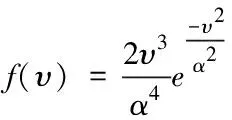
(7)

式中：

α

——原子的最可幾速率。

本文采用此速率分布進行模擬計算。

2.2.2

理想

π

躍遷基于上述理論基礎，建立銫原子Ramsey躍遷仿真模型。分別對理想和非理想情況下的躍遷線形進行模擬仿真。理想情況下，微波腔的兩個相互作用區沒有相位差(

φ

=0)、微波磁場的方向與C場平行并且C場恒定均勻。這時在最佳微波功率的條件下，銫原子超精細能級

m

=-3～3的7條理想π躍遷線形如圖4所示，從左至右依次為

m

=-3～3時的躍遷幾率，譜線關于中心躍遷(

m

=0)對稱，局部放大圖是中心π躍遷的躍遷線形。橫坐標中，

ω

是銫原子中心π躍遷角頻率，

ω

是饋入微波腔的微波角頻率，0-0躍遷對應的Ramsey峰值躍遷幾率最大，通常用作銫束頻標中的參考信號。實際躍遷線形往往不是理想情況，因此需要對每種因素進行逐個分析。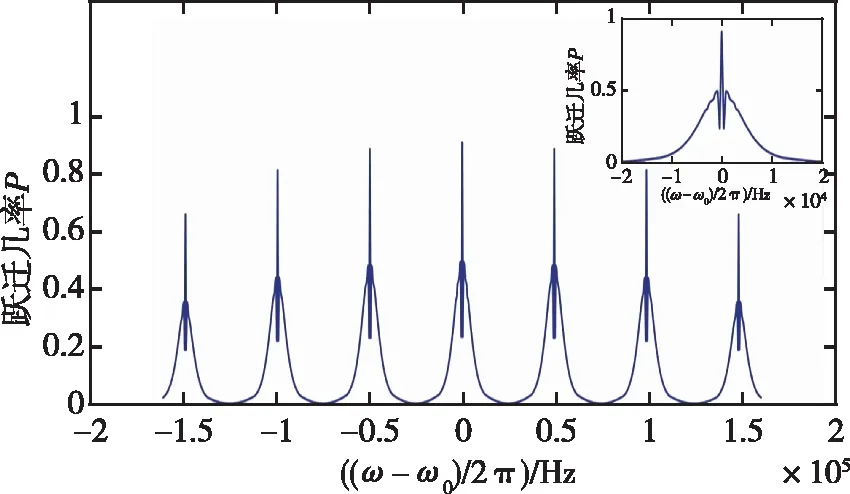

圖4 φ=0時理想的7條π躍遷線形圖Fig.4 The ideal 7 π transition lines whenφ=0

2.2.3

相鄰躍遷當微波高頻磁場與C場不平行時，可能產生

ΔF

=±1,

Δm

=±1的相鄰

σ

躍遷。對于中心躍遷來說，即產生(3,0)-(4,±1)的

σ

躍遷。圖5是

φ

=0時的7條π躍遷和14條

σ

躍遷線，局部放大圖是中心π躍遷及相鄰

σ

躍遷線形。其中(3,1)-(4,1)線的頻率比0-0線躍遷頻率高，(3,-1)-(4,-1)線的頻率則較0-0線低。每條π躍遷線((3,

m

)-(4,

m

))左右的兩條鄰態

σ

躍遷線分別為(3,

m

)-(4,

m

-1)和(3,

m

)-(4,

m

+1)。

圖5 φ=0時的7條π躍遷和14條σ躍遷線形圖Fig.5 7 π transition lines and 14 σ transition lines when φ=0

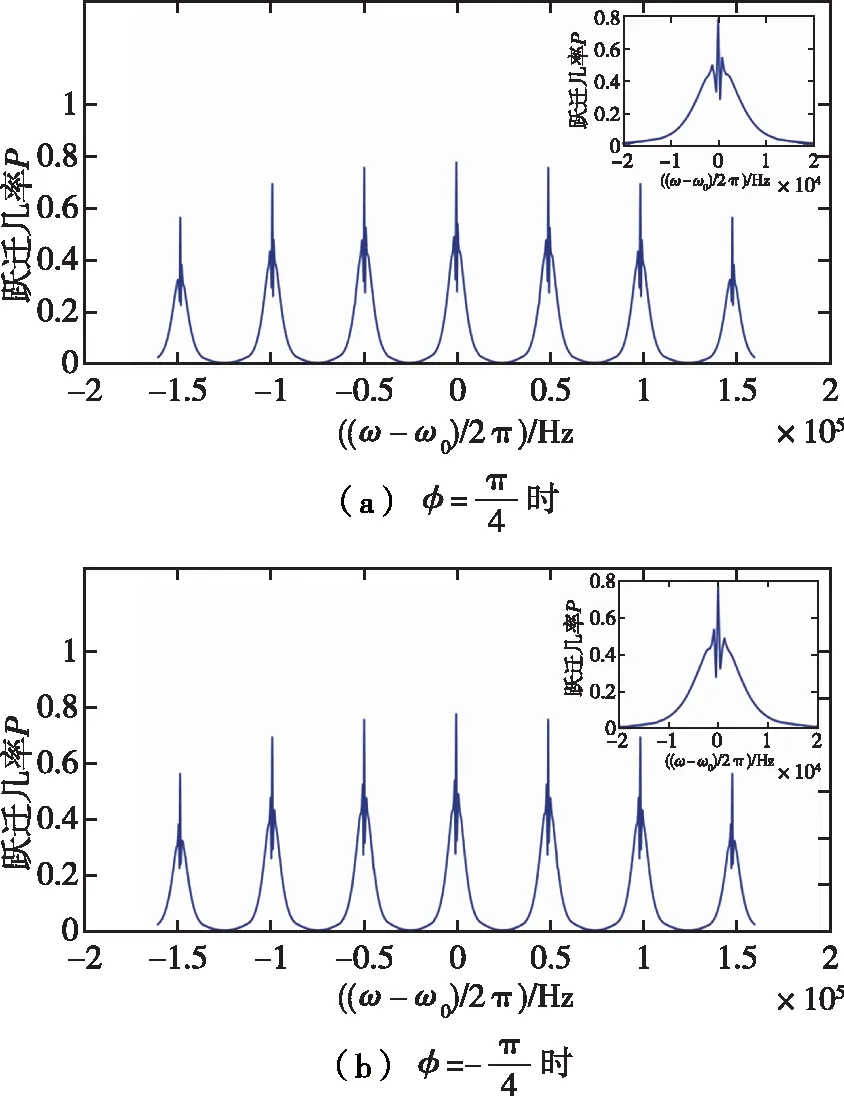
圖6 7條π躍遷線形圖Fig.6 7 π transition lines when

2.2.4

微波腔兩相互作用區存在相位差在理論計算躍遷幾率時，假定了兩個分離振蕩場的相位完全相同，但實驗中，這二者不可能絕對相同，因此在模擬計算中需要考慮腔相差對躍遷線形的影響。圖6(a)和圖6(b)是

φ

=±(π

/

4)時的7條π躍遷線，局部放大圖是中心π躍遷線形。可以看出，當存在腔相位差時，每條π躍遷線的中心躍遷頻率均會發生偏移。圖7是中心頻率的偏移隨腔相差

φ

的變化關系，可以看出腔相差

φ

越大，躍遷頻率偏移越大。當

φ

>0時，第一個振蕩場的相位比第二個振蕩場超前

φ

，中心頻率產生正向偏移；反之，第一個振蕩場的相位比第二個振蕩場滯后

φ

，中心頻率產生負向偏移。在銫束頻標中，兩個振蕩場的相位應盡量一致，以減小此類頻移。

圖7 腔相差φ變化時的π躍遷中心頻率偏移圖Fig.7 The π transition center frequency shift when the phase difference φ of the cavity changes

2.2.5

C

場不均勻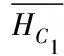

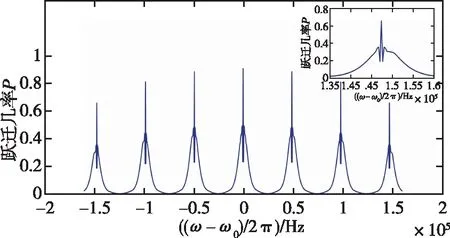
圖8 C場不均勻時的7條π躍遷線形圖Fig.8 7 π transition lines for the C field unevenness

3 銫原子Ramsey躍遷實驗研究

3.1 實驗方案

為了對建立的銫原子Ramsey躍遷仿真模型進行驗證，開展了銫原子Ramsey躍遷實驗研究，實驗方案如圖9所示，主要包括高真空腔室、銫原子束發射源、穩頻激光系統、微波互作用系統、原子熒光探測裝置。其中微波互作用系統是本文的主要研究對象，由微波腔、C場和磁屏蔽組成。其中微波腔為E面彎曲Ramsey型，C場由微波腔周圍密繞通電線圈獲得。在C場線圈周圍安裝磁屏蔽來消除環境磁場對C場的干擾。

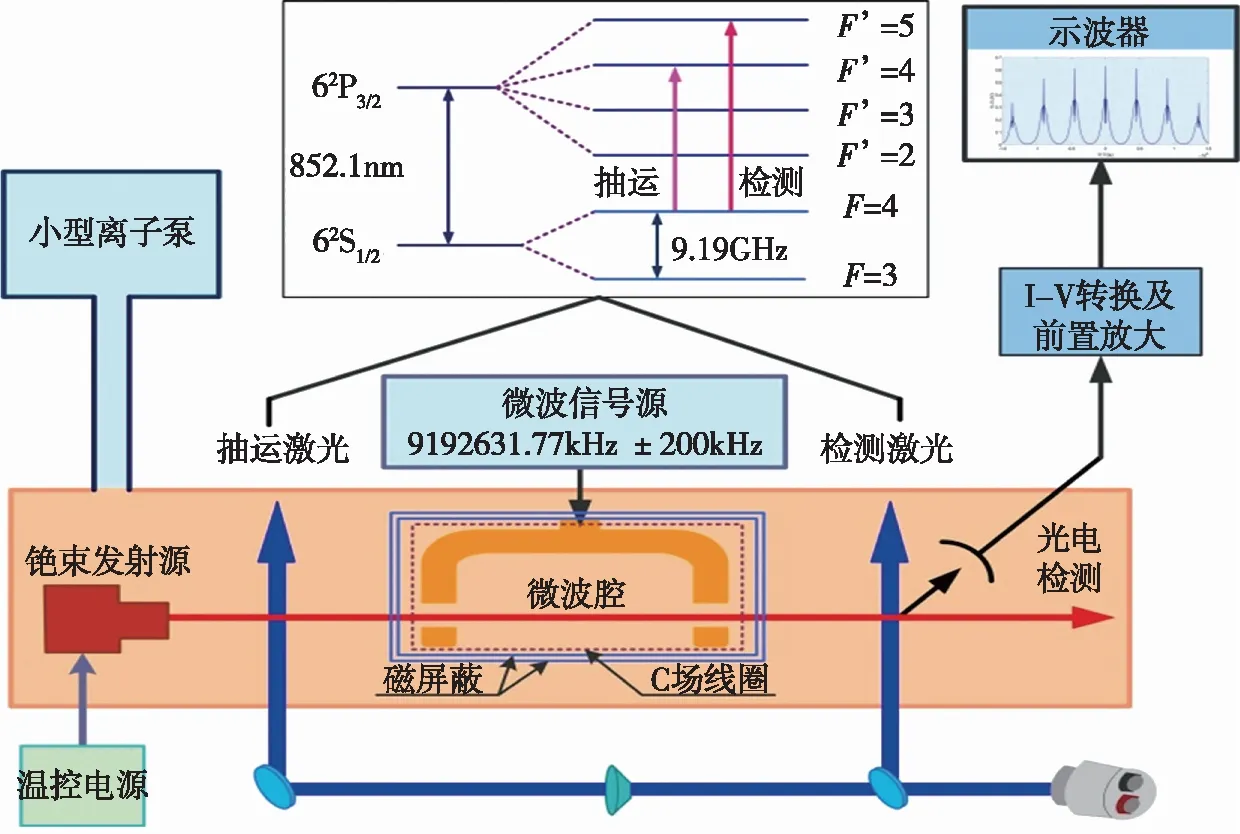
圖9 銫原子Ramsey躍遷實驗方案圖Fig.9 Experimental scheme diagram of Ramsey transition of cesium atoms

實驗過程中，用小型離子泵維持整個實驗裝置內部的高真空度。使用溫控電源將銫束發射源加熱到一定溫度，銫原子以熱束形式出射，到達抽運區后，在頻率鎖定至

F

=4→

F

′=4激光的持續作用下，所有

F

=4態的原子被制備到

F

=3態，

F

=3態原子進入微波腔后，在C場和微波高頻磁場的作用下發生超精細能級躍遷。到達探測區后，發生躍遷的原子被頻率鎖定至循環躍遷

F

=4→

F

′=5的激光探測并發出熒光信號，這些信號被收集并在光電檢測裝置中轉換成電流信號，經電流-電壓轉換和放大后被輸入示波器中。

3.2 實驗結果與分析

實驗中，掃描9 192 631.77kHz±200kHz之間的微波頻率，在示波器上觀察到如圖10所示的躍遷線形。為將實測躍遷線形與仿真線形區分開，實測躍遷線形用紅色表示，根據銫原子Ramsey躍遷仿真模型得到的仿真線形用藍色表示。可以看出，這組躍遷線形中存在許多由光、電、原子等因素引起的噪聲。本文主要是對躍遷線形進行研究，因此對線形中的噪聲進行平滑處理，并且將坐標軸進行單位換算與理論模型保持一致，得到如圖11所示的躍遷線形，左上角局部放大圖是

m

=-3時的躍遷線底部，相鄰兩側存在

σ

躍遷；右上角局部放大圖是

m

=-3時的躍遷線形。可以看出該線形存在以下問題：1)每條躍遷線兩側存在相鄰

σ

躍遷；2)每條躍遷線在Ramsey峰值左右是非對稱的，中心躍遷頻率朝著橫軸正半軸有微小偏移；3)除了中心躍遷之外，其它的Ramsey躍遷頻率與Rabi臺躍遷頻率不等。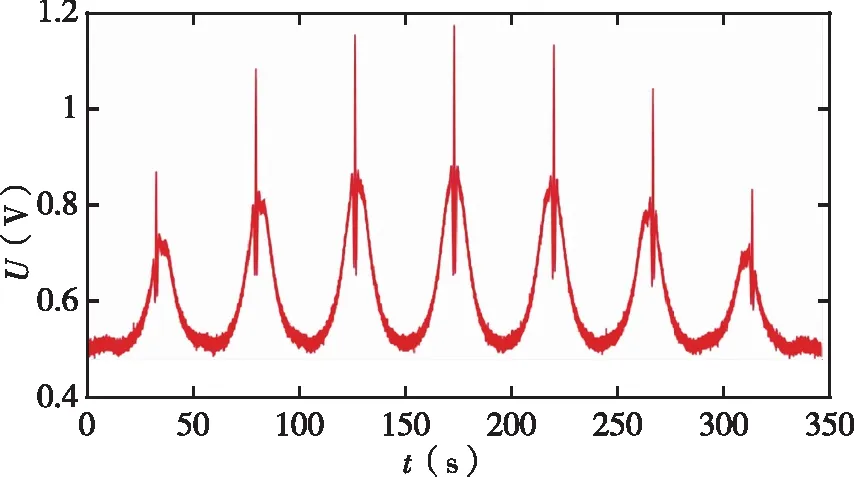

圖10 實驗測得的躍遷線形圖Fig.10 The transition lines obtained by experiment

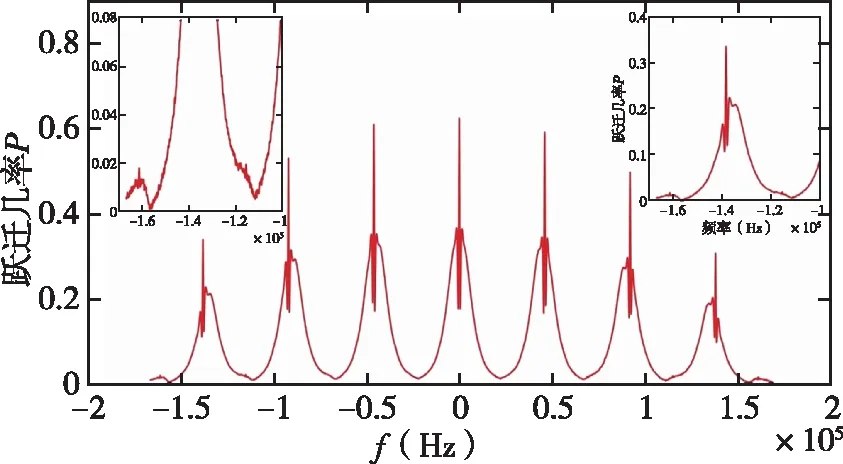
圖11 平滑噪聲后的躍遷線形圖Fig.11 The transition lines after smoothing noise

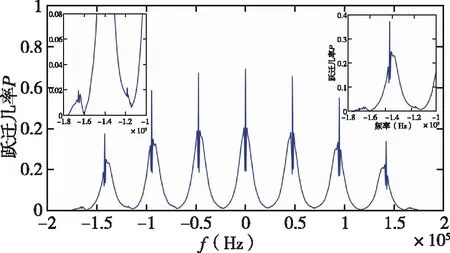
圖12 調節仿真模型中的參數得到仿真躍遷線形圖Fig.12 The simulation transition lines are obtained by adjusting the parameters in the simulation model

4 結束語

本文建立了一種銫原子Ramsey躍遷仿真模型，該模型可以對相鄰

σ

躍遷、腔相差以及C場不均勻時的躍遷線形進行仿真，并且開展了實驗研究。實測線形與該模型仿真的線形比對結果表明：通過多次調節模型中的參數可使仿真線形與實測線形高度一致，找出與理想情況出現偏差的參量，對后續實驗設計過程中線形的修正帶來很大幫助。因此銫原子Ramsey躍遷仿真模型的建立對分析實測線形具有重要的指導意義。下一步工作是對該模型進行完善優化，考慮融合更多頻移因素時躍遷線形的變化，并實現實驗線形和仿真線形的自動比對，快速得出各頻移因素與理想情況的具體偏差，推進銫束頻標的性能提升工作。