基于分形紋理特征的側掃聲吶圖像沉船識別方法研究

董凌宇，單瑞，劉慧敏，于得水，杜凱

1.中國地質調查局青島海洋地質研究所，青島266071

2. 青島海洋科學與技術國家實驗室海洋礦產資源評價與探測技術功能實驗室，青島266071

水下目標識別技術被廣泛應用于水下搜救、天然氣水合物探測、石油勘探、沉船搜尋、水下考古等領域[1]。其中，水下沉船識別技術在航道疏浚和安全保障、水下考古和文物發掘等多應用領域有著重要的意義。側掃聲吶系統具有測量范圍大、分辨率高等優點，可高效完成大面積海域的水下目標探測，廣泛應用于水下沉船識別工作。受復雜海洋環境影響，側掃聲吶的目標影像往往存在圖像模糊、畸變以及與其他成像體（如魚群或懸浮物等）相似度高等問題[2]。因此，高精度的側掃聲吶圖像分類提取算法是對沉船等目標進行有效識別的關鍵。

目前，側掃聲吶圖像的目標識別算法通常基于圖像分割法、支持向量機法、卷積神經網絡法、紋理特征分類法等。其中，基于圖像分割的方法主要根據聲吶圖像中遮蔽物體存在反射區與陰影區臨近的現象識別沉船，但其聚類往往受到巖體、海脊和沙波的干擾而出現誤識別[3]；支持向量機法使用沉船輪廓的不變矩進行沉船目標識別[4]，但由于其聲吶圖像多由測量實驗池獲得，缺失海底復雜地形與底質類型的特性，其運用于復雜海底環境存在一定局限性；卷積神經網絡法基于像素重要性值，通過提取圖像內點特征及其聚集度來識別目標，但由于聲吶圖像數據量較小，導致卷積神經網絡在分類時易存在過擬合的現象，錯將非目標物體識別為目標物體[5]。

受載體運動狀態及海洋環境噪聲影響，側掃聲吶圖像多存在目標邊界殘缺及目標被部分遮擋的問題，目標的形狀往往與實際有較大差異。對圖像中的特定目標識別時，同一類目標的輪廓存在多樣性且在不同的成像條件下其輪廓形狀也存在差異。由于人工目標不具有自然景物的自相似性紋理，紋理特征分類法對輪廓多樣的人工目標具有更好的識別效果。常用于側掃聲吶圖像目標識別的紋理特征有灰度共生矩陣GLCM（Gray-level Cooccurrence Matrix）和Tamura紋理。灰度共生矩陣基于圖像鄰域像素灰度值的概率分布提取紋理特征[6-7]，能較好描述具有方向性和灰度差異大的紋理圖像，但統計特征量的計算量龐大且特征量之間大多存在統計相關，尋找統計無關的特征量組合是一件繁雜的工作。基于人類對紋理視覺感知的心理學研究，Tamura在1978年提出圖像的六個特征值來描述圖像紋理[8]，其具有良好的旋轉不變性與尺度不變性，但對于圖像局部紋理特征難以描述。分形紋理基于圖像像素灰度值的空間分布與自相似性描述提取圖像紋理特征。Hausdorff提出分形維數用于定量描述圖像表面的空間復雜程度，能夠定量描述目標的紋理特征。Grassberger進一步使用多重分形譜用于描述不同測度子集下的局部圖像紋理特征，能夠結合整體紋理與局部紋理的相對關系描述目標特征。同時分形紋理特征提取避免了人工干預的低效，因而是一種良好的目標識別方法。

本文針對三種分形紋理特征提取，實現了盒計數分形算法、雙毯覆蓋模型分形算法與多重分形譜分形算法。針對側掃聲吶小樣本目標識別易過擬合、分類精度低等問題，采用解釋性好、抗干擾強的Adaboost級聯分類器，構建基于分形紋理特征的Adaboost級聯分類器沉船目標識別流程，并采用精確率和召回率的調和平均值F1作為沉船識別精度評價標準。結合實測數據進行沉船識別實驗，分析比較了三種分形紋理特征的識別效果，并與灰度共生矩陣GLCM和Tamura紋理特征的識別結果進行對比，驗證了本文方法的有效性。

1 分形理論與分形紋理特征

近年來，分形理論在圖像處理領域中取得了廣泛的應用，包括邊緣檢測、目標識別、壓縮編碼等[9-12]，其中已在遙感圖像、醫學圖像以及交通圖像分類識別中取得一定成果[13-15]。分形是用于描述集合的空間復雜程度的一種度量，能夠定量地描述圖像表面的復雜性和不規則度。因此分形維數可以用于描述圖像紋理特征。Grassberger提出了多重分形譜來描述不同測度子集下的局部圖像紋理特征，能夠從局部到整體全面地描述目標特征，這也為更準確的目標識別提供了理論依據[16]。

分形維數可用于描述二維圖像表面紋理的復雜程度，Hausdorff定義了分形理論中關于測度和維數這二者的概念[17]。Hausdorff測度外延了在傳統歐幾里得幾何學中所描述的長度、面積和體積的概念，其所能描述的對象既可以是歐氏幾何圖形，也可以是分形。定義H s（F）為F的s維Hausdorff測度，隨著s的變化，存在使H s（F）從∞變化到0的臨界值s0，其定義為Hausdorff維數，記作dH（F），即：

Hausdorff維數對于任何集合都適用，因此具有很高的理論價值，但Hausdorff維數難于直接計算，本文采用下面的盒維數和毯維數進行簡化計算。

1.1 盒維數

Gangepain和Roques-Carmes在1986年 提 出 基于盒計數（Box-counting）的分形維數，通過計算覆蓋圖像表面的最小盒子數來度量[18]。將M×M的圖像分為N×N的子塊，圖像（x,y）處的灰度值為f（x,y），總的灰度級為G。此時將圖像看作三維物體的表面灰度集（x,y,f（x,y））。XY平面上是N×N的網格，Z軸為網格內像素灰度值，每個網格上有若干個盒子疊加，盒子高度h=[G×N/M]。

若在第（i,j）個網格中，第m個盒子中包含網格內灰度最小值，第l個盒子包含網格內灰度最大值，則覆蓋第（i,j）個網格的盒子數nr（i,j）為：

覆蓋整個圖像的盒子數Nr為：

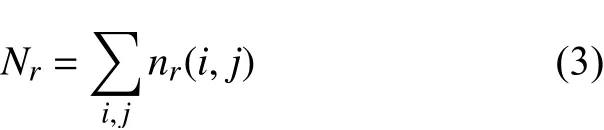
其中r=M/N，由此可求分形維數D為：

通過改變網格N的大小計算一組Nr，然后計算點對{log（1/r）,log（Nr）}的線性回歸，其斜率即是分形維數D。

1.2 毯維數

Mandelbrot在計算英國海岸線長度時提出了毯維數算法。近年來，國內也有應用毯維數進行海岸線長度計算的案例，取得了較好的效果[19-20]，其后衍生出可用于描述圖像紋理的基于雙毯覆蓋模型的分形算法。圖像的“毯子”由各像素灰度值作Z軸所形成的三維曲面上下ε處構建，其厚度為2ε，表面積為體積除以2ε。

令f（i,j）表示灰度函數，με表示“毯子”的上表面，bε表示“毯子”的下表面，初始情況設為：

“毯子”生長算法如下：

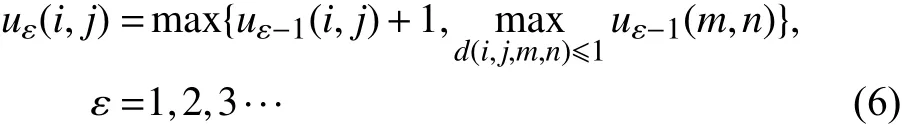
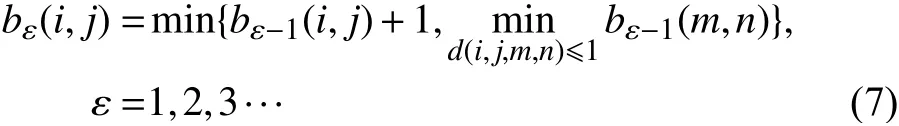
其中，d（i,j,m,n）為（i,j）與（m,n）兩點間的距離。則“毯子”的體積為：

表面積為：

由于分形表面積為A（ε）=Fε2-D，其中D為分形維數，令c1=2-D，則

改變尺度ε的大小，可以計算得到一組logA（ε）的值，然后計算點對{ε,logA（ε）}線性回歸，得到回歸方程的斜率c1，即可求出分形維數D。

1.3 多重分形譜

多重分形常用來描述圖像的奇異性幾率分布，其能夠量化測度的奇異結構，以及在尺度發生變化時以伴隨有不同范圍冪定律的現象建立模型，因此能夠用于描述圖像的紋理特征[21]。設α為Lipschitzholder指數，又稱奇異性指數，其決定了概率密度的奇異性。首先計算圖像上每個點的奇異指數α，將具有相同奇異指數的像素點作為一個點集；然后計算具有不同奇異指數像素點集的分形維數，即可以得到多重分形譜圖像α-f（α）[22]，計算過程如下：

（1）用尺度為δ的盒子覆蓋圖像，將像素點落在第i個盒子概率定為pi（δ），即得到概率測度分布為：

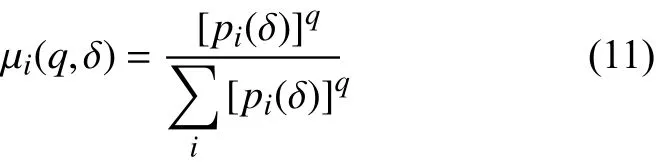
其中，∑i[pi（δ）]q為所有盒子概率的q階矩之和。

（2）對于概率測度分布的q階矩，理論上q的取值范圍為-∞＜q＜+∞。當q＞0時，在概率測度求和中具有較大概率的子集對分形維數的貢獻較大；當q＜0時，具有較小概率的子集對分形維數的貢獻較大。

此時，奇異指數α（q）為：

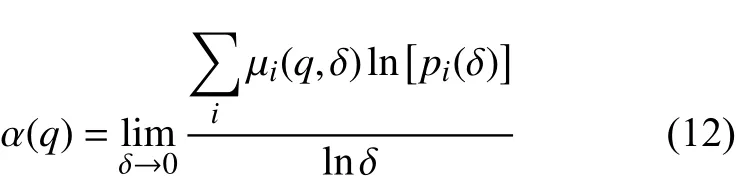
分形維數f（α（q））為：

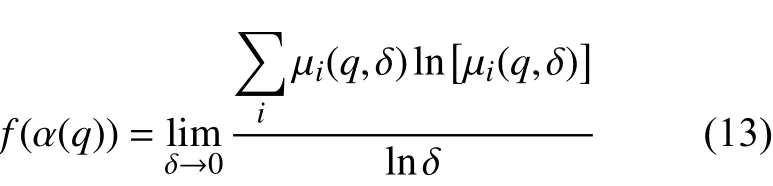
（3）取一組不同的q值重復上述計算過程，繪制每個奇異指數α（q）對應的分形維數f（α（q））即得到了多重分形譜α-f（α）。其中α-f（α）曲線包括最小奇異指數αmin、最大奇異指數αmax、最小分形維數值fmin、最大分形維數值fmax、多重分形譜寬Δα=αmax-αmin和多重分形譜高Δf=fmax-fmin。

多重分形譜能夠用來描述紋理圖像的層次特征，即具有不同奇異指數的局部圖像紋理。在區分自然場景中的人造物體時，人造物體本身不具有自相似性結構的特點，不滿足分形模型，而自然景物存在自相似性，滿足分形模型[23-24]。因此，沉船目標與海底表面的分形維數不同，便可以實現分形紋理對沉船識別的特征描述。多重分形方法通過奇異指數考慮了圖像的局部與不同層次的紋理特征，因而能夠全面且準確地描述圖像分形結構，從而區分自然場景與人工造物，提高沉船目標識別的有效性。

2 基于分形紋理特征的Adaboost目標識別

級聯分類器Adaboost是一種基于boosting算法的改進算法，即是把“弱學習算法”提升為“強學習算法”，在人臉識別、交通標志檢測、醫學影像識別中均取得了良好的效果[25]。如圖1所示，其通過選取多個弱分類器按照給定的樣本集進行訓練，每一個弱分類器的分類結果按照不同的權重對最終分類結果進行貢獻。

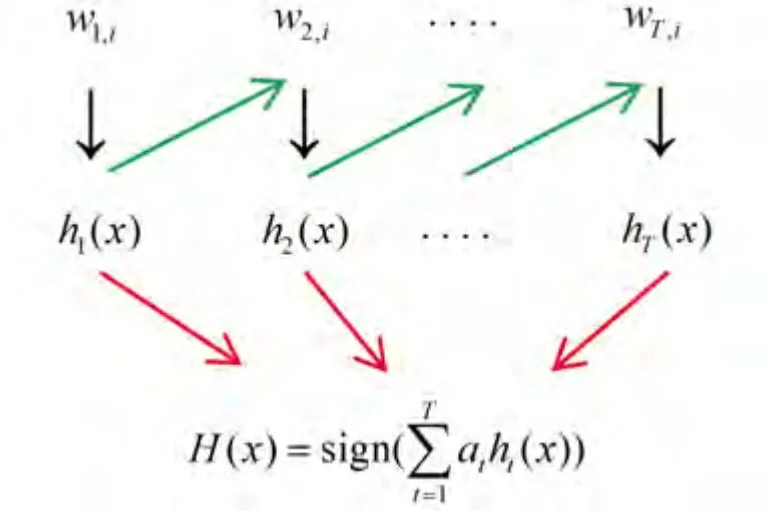
圖1 Adaboost級聯分類器Fig.1 Adaboost cascade classifier

2.1 Adaboost分類器介紹

本文采用簡單決策樹為弱分類器的Adaboost級聯分類器作為側掃聲吶圖像沉船識別分類器，主要計算過程如下：

（1）設 訓 練 樣 本 集 為S=（x1,y1）,（x2,y2）,···（xm,ym），若yi取值為-1或+1，則為二分類問題，其中1,···,m為樣本編號，ym為樣本類別的標記。初始化樣本權值w1,i=1/m，迭代次數為t=1,2,···,T。

（2）首先調用弱分類器學習算法，計算加權分類誤差，再通過最小化加權分類誤差ε選取一個最佳的分類器h（x,f,p,θ），其中p為不等號方向，f為特征向量，θ為閾值參數。

（3）令ht（x）=h（x,ft,pt,θt）,ft,pt,θt為使εt最小時的因子，則更新下一輪迭代權重為，wt+1,i=wt,iexp（-atytht（xi））/Zt，其中Zt為歸一化因子。

（4）輸出強分 類 器at=ln（（1-εt）/εt）。

Adaboost算法的工作機制是從訓練集初始權重訓練出弱分類器1，根據其分類誤差來更新訓練樣本的權重，使得誤差較高的樣本在弱分類器1中的權重變高，從而在接下來的弱分類器2中得到更多重視，如此重復進行直到指定的T個弱分類器訓練完畢，通過集合策略進行整合得到最終的強分類器。因此，Adaboost分類器具有分類精度高、弱分類器可用多種回歸分類模型構建、結構簡單易理解、更能抵抗過擬合等優點。其他常用于二分類的分類器中，卷積神經網絡容易發生過擬合、中間過程不可解釋；K最近鄰算法每一次分類均會重新全局運算，效率較低且需要人工K值選擇；支持向量機對于小樣本分類具有優勢，但核函數可解釋性較差。因此本文采用簡單決策樹為弱分類器的Adaboost級聯分類器作為側掃聲吶圖像沉船識別分類器。

在機器學習和目標分類等領域中，如何評估分類結果的精度是一個重要的工作，本文引入Fmeasure評價模型[26]。F-score是精確率P和召回率R的加權調和平均，當參數α增大時，召回率的權重增加，精確率的權重降低；當參數α減小時，召回率的權重降低，精確率的權重增加。

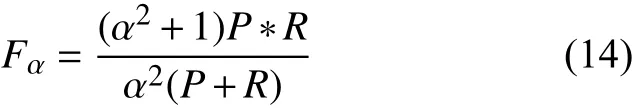
當參數α=1時，即認為精確率和召回率的權重是一樣的。此時F1值就是精確率和召回率的調和平均值，能夠較為準確地評價分類器分類結果，即：

2.2 Adaboost目標識別流程

本文構建了基于分形紋理特征的Adaboost目標識別流程，如圖2所示。

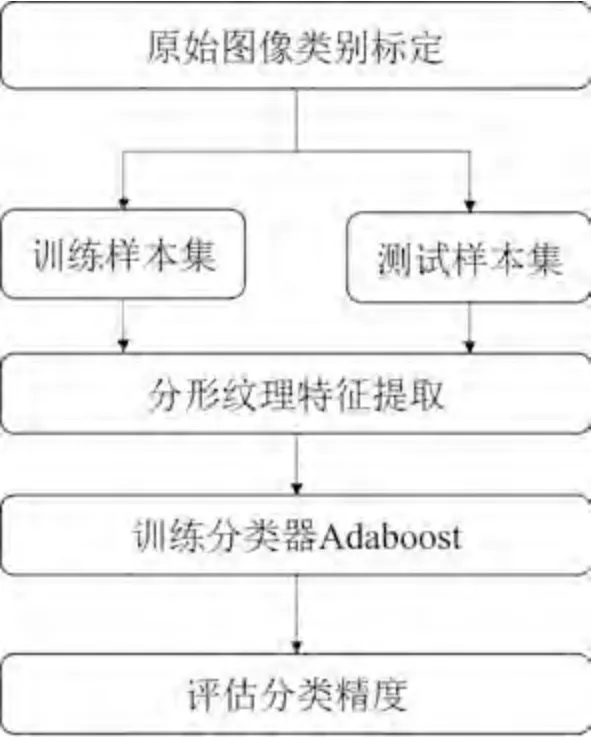
圖2 基于分形紋理特征的Adaboost目標識別流程Fig.2 Adaboost target recognition procedure based on fractal texture features

第1步，將樣本分為訓練樣本和測試樣本兩部分（均已人工標定其類別標簽），訓練樣本與測試樣本中均包含若干沉船圖像和非沉船圖像。

第2步，根據盒維數、毯維數與多重分形譜計算流程，計算訓練和測試樣本的分形紋理特征向量。

第3步，將訓練樣本的分形紋理特征向量輸入級聯分類器Adaboost中進行訓練，然后輸入測試樣本的分形紋理特征向量，預測每一個測試樣本的類別。

第4步，根據分類器分類結果計算F1值。

針對側掃聲吶小樣本目標識別易過擬合、分類精度低的問題，常用分類器在使用中存在一定問題難以解決，如支持向量機解釋性較差，卷積神經網絡容易過擬合，K最近鄰算法計算效率低且參數需人工干預。因此本文采用解釋性好、抗干擾強的Adaboost級聯分類器，構建基于分形紋理特征的Adaboost分類器沉船目標識別流程，并使用精確率和召回率的調和平均值F1作為沉船識別精度評價標準。

3 實驗與討論

3.1 基于分形紋理特征的Adaboost識別實驗

本文通過選取各個側掃聲吶儀器廠商網站以及沉船搜尋網站上展列的側掃聲吶圖片為包含沉船目標的正樣本，共47張，通過截取普利茅斯灣側掃數據不包含沉船目標的負樣本（魚和海底表面）共105張圖片，圖片大小為128×128。隨機選取正樣本28張、負樣本71張作為訓練數據來訓練分類器，余下的正樣本19張、負樣本34張作為測試數據來測試分類器的訓練效果（圖3）。

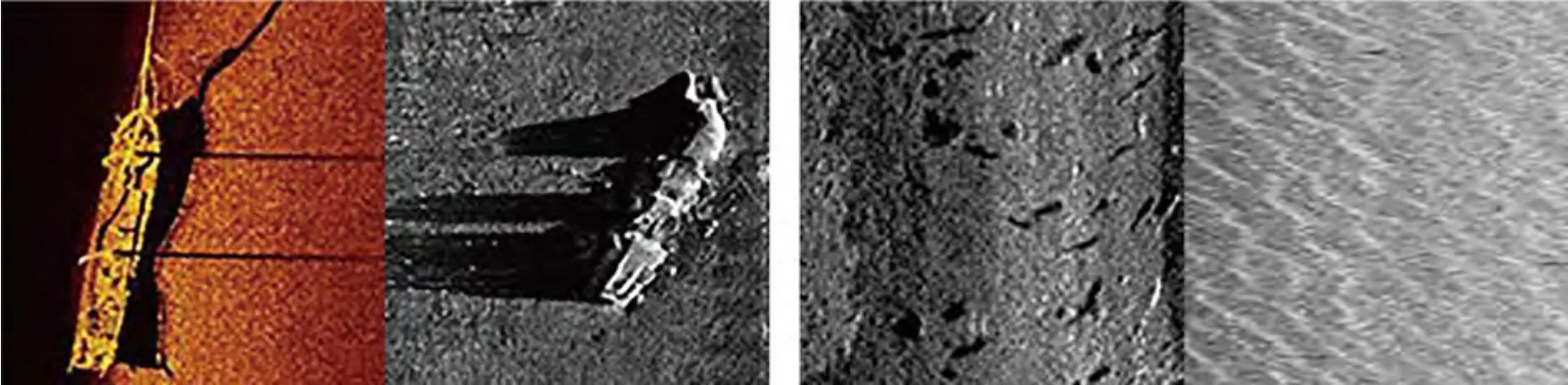
圖3 目標識別中的正樣本與負樣本左為正樣本示例[27]，右為負樣本示例。Fig.3 Positive and negative samples in target recognitionLeft is positive sample,right is negative sample.

（1）盒維數分類結果

根據1.1節提出的盒維數計算方法計算得到每張圖像對應的盒維數值。圖4展示了部分沉船目標和非目標的盒維數。

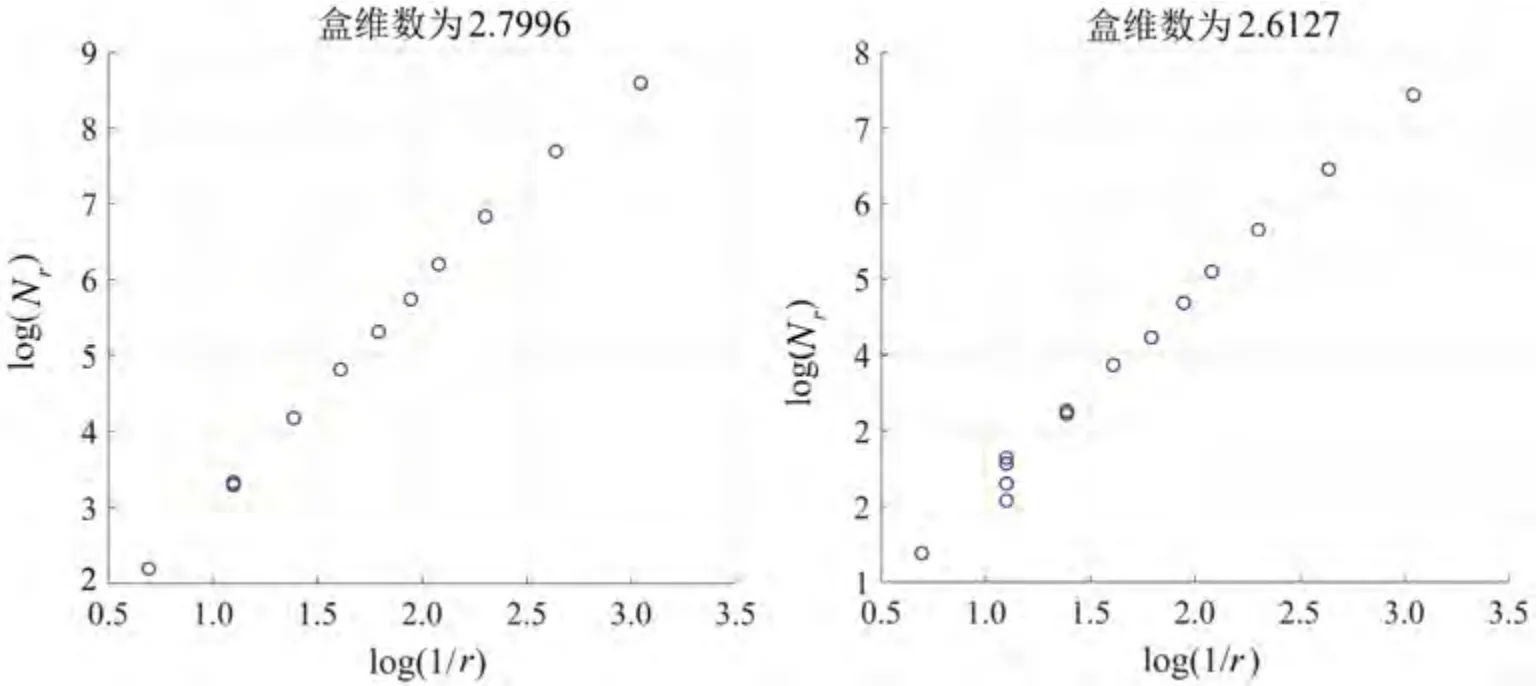
圖4 盒維數計算左為正樣本結果，右為負樣本結果。Fig.4 Box dimension calculationLeft is positive sample result,right is negative sample result.

（2）毯維數分類結果

對于給定的毯子厚度ε可以求出其毯維數值，在此通過對比不同毯子厚度ε對分類結果的影響來尋找最佳毯子厚度，如圖5所示。

由圖5可知，隨著毯子厚度的增大，沉船識別的精確率大體逐漸上升，而沉船的召回率逐漸下降，表明當毯子厚度大于100時，召回率較低，表示毯維數對沉船圖像紋理特征描述過擬合，從而降低了對不同情況下沉船目標的描述程度，即識別沉船的能力不足。此時F1值在毯子厚度為90時取得最大值83.3%。因此本文選擇毯子厚度為90時的毯維數作為其最優紋理特征。

圖5 不同毯子厚度的分類結果比較Fig.5 Comparison of classification results of different blanket thicknesses

（3）多重分形譜分類結果

根據1.3節提出的多重分形譜計算公式，本文繪制了沉船正樣本和其他非沉船負樣本的α-f（α）多重分形譜，如圖6所示。部分沉船及非沉船目標多重分形譜參數見表1。

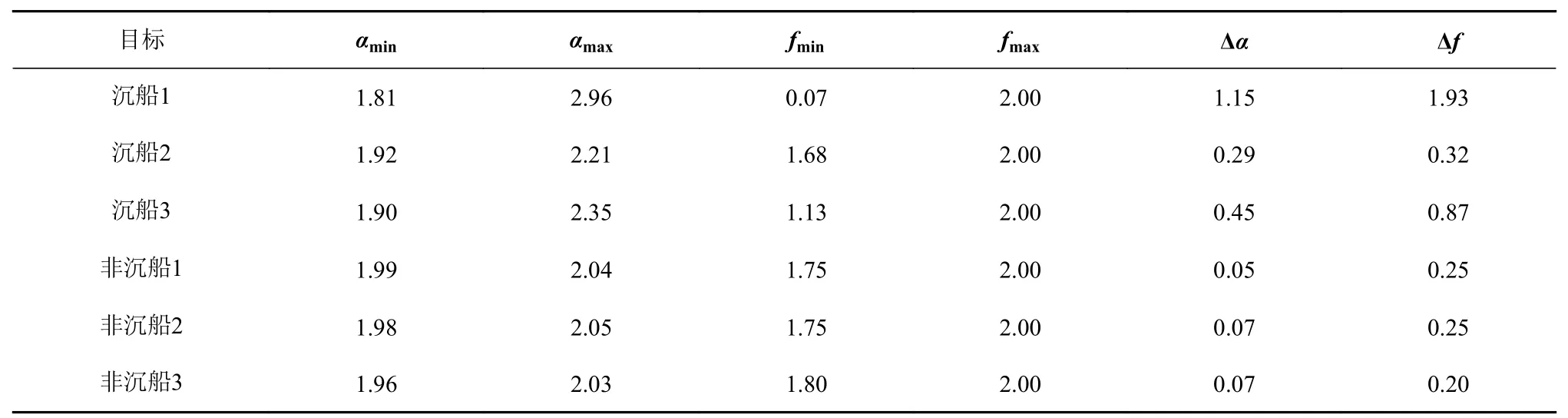
表1 沉船及非沉船目標的多重分形譜參數Table 1 Parameters of multifractal spectrum of shipwrecked and non-wrecked targets

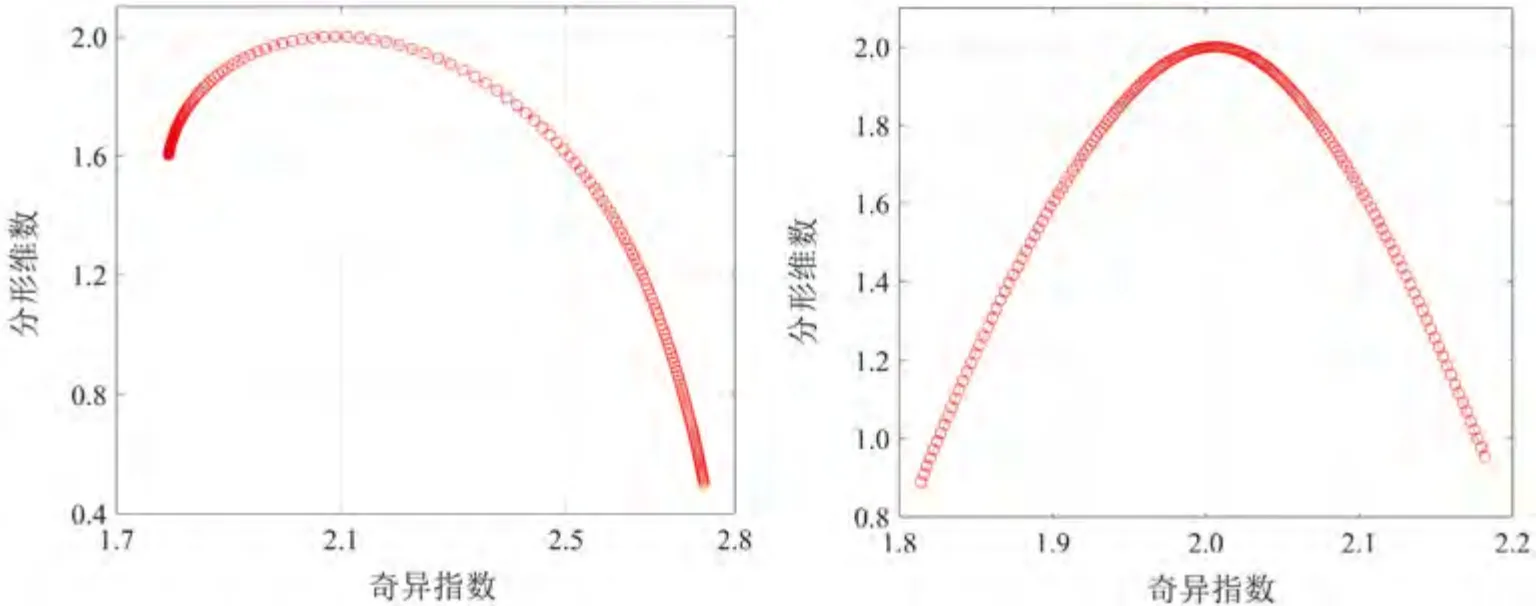
圖6 不同樣本的多重分形譜結果左為正樣本，右為負樣本。Fig.6 Multifractal spectrum of different samplesLeft is positive samples,right is negative samples.Horizontal axis α is singularity index,and vertical axis f（α）is fractal dimension.

3.2 三種分形紋理特征識別結果與討論

比較了盒維數、毯維數、多重分形譜三種分形紋理特征提取方法對側掃聲吶圖像沉船目標的識別效果，如表2所示。

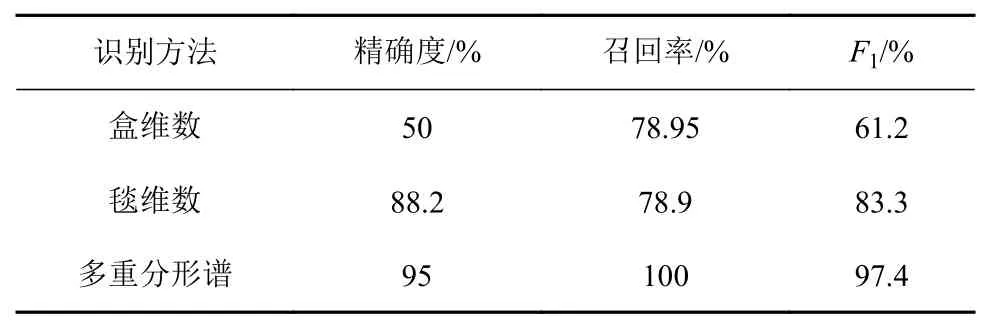
表2 分形紋理特征識別結果Table 2 Recognition of fractal texture feature

在三種分形紋理特征中，多重分形譜特征的精確度和召回率均遠高于盒維數與毯維數兩種分形紋理特征，其F1值為97.4，高于盒維數的61.2與毯維數的83.3，因而多重分形譜的側掃聲吶圖像沉船目標識別效果最好，這表明多重分形譜紋理特征對沉船目標的描述全面性和分辨沉船目標與非目標區的區分能力較其他兩種方法要好。

單一分形維數（盒維數和毯維數）盒維數紋理特征識別效果最差，其原因是其僅僅反映的是單一尺度下整張圖像的紋理復雜程度，無法描述圖像局部紋理信息，對于一些整體紋理較為復雜的非沉船目標，如含有魚群的聲吶圖像，往往會誤判為沉船圖像，因此其從非沉船目標中對沉船目標的區分性不足，識別的精確率較低。

多重分形譜紋理特征的優點在于對不同的圖像概率測度子集分別計算其分形維數，有效地描述了圖像局部紋理特征，即使存在某些魚群或海底地表的紋理在整體上和沉船目標上較為相似，其局部紋理特征也往往存在明顯的差異，且不同種類的目標其多重分形譜的性質區別很大，因而多重分形譜獲得了很好的沉船識別效果。

3.3 其他紋理特征識別結果與討論

為了驗證分形紋理特征在側掃聲吶圖像沉船目標識別中的效果，本文擬采用兩種常用的紋理特征提取方法作為對比實驗，即灰度共生矩陣GLCM與Tamura紋理特征。GLCM選擇最常用的6個特征值即角二階距、逆差距、熵、對比度、非相似性、相關性。計算特定距離d下的4個方向的灰度共生矩陣，用6種特征值的均值與方差作為其特征向量，以抵消沉船的方向性對于目標識別的干擾。Tamura選擇六特征值作為圖片的特征向量，即粗糙度、對比度、方向度、線性度、規整度和粗略度。實驗數據與分類器選取均與3.1節相同，沉船目標識別結果見表3所示。

表3 多重分形譜、GLCM、Tamura三種紋理特征識別結果Table 3 Recognition results of multifractal spectrum,GLCM and Tamura

從圖像尺度的角度考慮，Tamura紋理特征所提取的六特征值僅有規整度一個值能夠描述圖像的局部特征，其他5個特征值均是對整張圖像的尺度進行灰度統計的結果，因而很難全面描述沉船圖像的紋理特征；而GLCM對距離參數d的取值不同可以理解為統計不同尺度下的圖像局部特征（像素點對灰度值出現頻率）來描述沉船圖像的紋理特征，因此，當尋找到最佳距離參數d時則表明在該尺度下獲取的紋理特征對沉船描述最好，因而識別效果較好；在多重分形譜方法中，通過不同奇異指數將圖像劃分為不同測度子集，統計每一個子集的紋理特征形成多重分形譜。從多尺度的角度將沉船圖像整體到局部的紋理特征結合起來描述沉船目標，取 得了最優的識別結果。

4 結論

（1）在三種分形紋理特征中，多重分形譜特征的識別精度F1遠高于單一分形維數（盒維數與毯維數）。單一分形維數識別效果差，其原因是其僅僅反映單尺度下整張圖像的紋理復雜程度，無法描述多尺度局部紋理信息。多重分形譜紋理特征對圖像中不同的概率測度子集分別計算其分形維數，有效地描述了圖像局部紋理特征。某些負樣本整體紋理和沉船目標較為相似，但其局部紋理特征也往往存在明顯的差異，在不同種類目標的多重分形譜上的譜型區別很大。多重分形譜能夠從多尺度角度將正負樣本進行區分，因此獲得了最優的沉船識別效果。

（2）Tamura紋理特征六特征值中僅有規整度描述圖像的局部特征，其他5個特征值均是對整張圖像的尺度進行灰度統計的結果，因此識別精度F1優于單一分形維數，但弱于灰度共生矩陣和多重分形譜特征。灰度共生矩陣通過調整距離和方向參數來尋找識別效果最好的圖像局部紋理特征，但此方法對每張圖像都要重新尋找最佳參數，時間成本更高。因此相對常用的紋理特征，多重分形譜特征具有能夠描述多尺度局部紋理，避免人工干預，識別效率高等優點，在沉船識別中也獲得了最優的識別精度和識別效率。