MIMU/偏振光擬牛頓優化航姿求解方法

金仁成 魏巍 孫慶飛 洪金輝 姜佳旭

摘要：針對傳統磁力計/MIMU組合導航系統存在的抗電磁干擾能力弱、適應性差等問題，提出了一種基于大氣偏振分布模式的無人機導航航姿無約束優化求解方法。融合陀螺儀、加速度計、偏振光傳感器測量數據，構建基于改進擬牛頓法的姿態最優化解算模型，其中，該模型以最優化理論為基礎，引入實時四元數微分構建動態步長因子，預測姿態更新趨勢;設計狀態判斷閾值，自適應判斷飛行狀態，提高解算精度。實驗結果表明，這種方法得到的姿態角靜態性能穩定，同時，在動態環境中，該方法得到的姿態角誤差值最小，較梯度下降法精度提高50%，較共軛梯度法精度提高37%～50%，表現出較好的動態收斂性與誤差穩定性，動態精度較高，能夠較準確跟蹤姿態變化，可以有效提高偏振光輔助的捷聯慣導組合導航系統航姿估計的準確性與可靠性。

關鍵詞：偏振光;MIMU;航姿解算;擬牛頓

中圖分類號：V249???????????? 文獻標志碼：A

文章編號：1009-9492（2021）12-0023-06

開放科學（資源服務）標識碼（OSID）：

MIMU/ Polarized Light Quasi-newtonian Optimization Method for Attitude Solving

Jin Rencheng ，Wei Wei ，Sun Qingfei ，Hong Jinhui ，Jiang Jiaxu

（School of Mechanical Engineering， Dalian University of Technology， Dalian， Liaoning 116024， China）

Abstract： Aiming at the problems of the traditional magnetometer /MIMU integrated navigation system， such as weak anti-electromagnetic interference? ability? and? poor? adaptability，? an? unconstrained? optimization? method? for? UAV? navigation? attitude? was? proposed? based? on atmospheric polarization distribution mode. The attitude optimization model based on the improved quasi-Newton method was constructed by integrating the measurement data of gyroscope， accelerometer and polarized light sensor. Based on the optimization theory， the dynamic step factor was constructed by introducing real-time quaternion differential to predict the attitude updating trend. The threshold value of state judgment was designed， and the flight state was judged adaptively to improve the precision of solution. Attitude angle of the experimental results show that the approach of static performance is stable， at the same time， in a dynamic environment， the method to get the minimum value attitude angle error， the gradient descent method precision is increased by 50%， the conjugate gradient method precision is increased by 37%～50%， show a good dynamic stability， convergence and error dynamic accuracy is higher， can accurately track the attitude change， it can effectively improve the accuracy and reliability of attitude estimation of strapdown inertial navigation system assisted by polarized light.???? Key words： polarized light; MIMU; navigation position calculating; quasi-newton

0 引言

隨著微機電系統（MEMS）工藝和計算機技術的發展，小型無人機多采用低成本的 MEMS傳感器（主要有陀螺儀、加速度計、磁力計）作為姿態估計設備。其中，陀螺儀是姿態角度估計的關鍵傳感器，但由于其固有誤差，長時間累計積分運算，會存在嚴重漂移現象，通常利用加速度計補償陀螺儀的俯仰角和橫滾角偏差，利用磁強計補償航向角偏差。但是磁強計易受地磁場與電磁場的干擾，不能用于某些特殊環境。因此，進一步研究高精度、高可靠性的組合導航系統成為了無人機導航控制領域的研究熱點。

通過觀察一些鳥類和昆蟲的自主導航行為，科學家發現某些生物能夠通過感知自然光經過大氣散射后形成的偏振光用于導航。近年來，國內外研究人員對偏振光在導航中的應用開展了各種研究[1-5]，2011年，大連理工大學的褚金奎課題組將偏振光傳感器運用于移動機器人上，實現移動導航。2012年，德國學者 Wolfgang以及澳大利亞學者 Javaan Chahl ，分別嘗試將偏振光傳感器搭載于四軸無人機與固定翼無人機上進行實驗。2014年，中國科技大學通過與中科院先進制造所合作，將成像式偏振光導航傳感器應用到了汽車導航系統。2019年，西北工業大學的周軍等提出一種基于偏振光傳感器和磁力計的姿態確定方法，驗證了其估計衛星姿態信息的可行性。

現階段關于偏振光導航的研究主要集中在地面二維平面以及偏振光原理研究上，在無人機導航等三維空間的應用仍處于起步階段。目前偏振光在組合導航系統中多以輔助慣性導航系統定姿為主，主要是通過卡爾曼濾波算法或互補濾波算法實現姿態估計。但卡爾曼濾波算法受誤差估計模型影響，易發生濾波精度下降甚至發散的情況，計算精度受噪聲影響明顯。互補濾波算法需要對比例參數與積分參數進行估計，參數估計隨機性會影響補償的效果[6-9]。

針對現階段偏振光輔助導航系統的優勢與不足，本文基于大氣偏振光分布模式提出了一種航姿無約束優化求解方法，設計動態步長因子與狀態閾值，提高了姿態求解的精度與效率，通過實驗驗證了該方法可以提高基于偏振光輔助的航姿參考系統的姿態估計準確性與可靠性，為無人機仿生導航提供了一種可靠的姿態求解方案。

1 偏振光傳感器輔助定姿原理

1.1 姿態坐標系描述

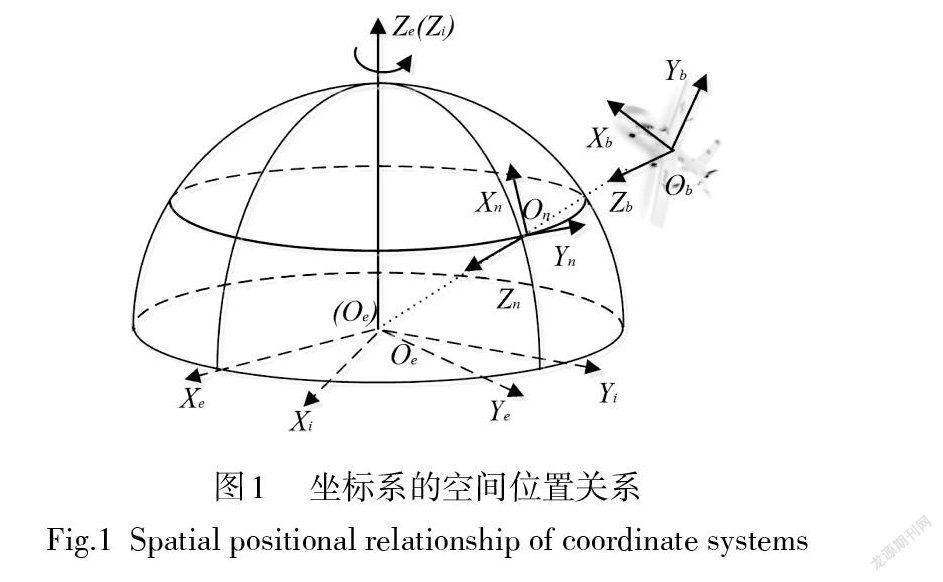
飛行器的空間姿態本質上是機體坐標系（b 系）與導航坐標系（ n 系）的姿態關系，本文導航坐標系原點選在飛行器質心，Xn 軸指向地理北向（north）， Yn 軸指向地理東向（east）， Zn 軸指向地心方向。機體坐標系原點選在飛行器質心，Xb 軸沿機體縱軸指前， Yb 軸沿機體橫軸指右，Zb 軸指向機體下方，坐標關系如圖1所示。

1.2 四元數姿態更新

目前對于無人機姿態更新主要有歐拉角法、四元數法和方向余弦法等。歐拉角法形式直觀、易于理解，但存在90°奇異性問題。方向余弦法采用方向余弦矩陣存儲姿態信息，每次更新需計算9個參數，計算量大。四元數法求解不存在奇異性問題，只需計算4個參數，方法簡單，計算時間短[10-12]。因此本文采用四元數法描述姿態更新過程。

四元數的物理意義表示了轉軸方向與轉角大小，其三角式表達為：

四元數微分方程為：

其矩陣表達為：

其中，四元數為 Q =q0 q1 q2 q3T? ，載體角速度為ωb =ω bx?? ω by?? ω bzT 。

無人機飛行姿態的變化可以理解為載體坐標系（b系）相對于導航坐標系（ n 系）的旋轉，本文將導航坐標系到載體坐標系的姿態矩陣定義為 Cnb ，同時用四元數進行表示，即：

通過將三姿態角表示的姿態旋轉矩陣與用四元數表示的姿態矩陣對應可用四元數對3個姿態角進行表示，即：

式中：γ為橫滾角;θ為俯仰角;ψ為航向角。

1.3 偏振光輔助導航定姿模型

太陽光遇到大氣微粒分子發生散射會產生光的偏振，并形成穩定的大氣偏振分布模式，本文利用偏振光傳感器檢測天空中偏振光分布模式[13]。由 Rayleigh 散射原理可知，最大偏振光矢量（E ）總是垂直與太陽矢量（S）與觀測矢量（Z ）所成平面，由此可建立偏振光傳感器理論測量模型，如圖2所示。

為方便說明，引入偏振光傳感器測量坐標系 m 系和太陽坐標系p 系，其中，原點為偏振光傳感器質心，Xm 軸為偏振傳感器參考軸方向，Zm 軸為偏振光傳感器觀測偏振矢量方向， Ym 軸與前二軸構成右手笛卡爾坐標系，太陽坐標系三軸則分別指向地理的西向、南向、天向。

太陽在太陽坐標系中的位置可以由太陽高度角和太陽方位角表示，二者滿足：

式中：φ為地理緯度;δ為太陽的赤緯;τ為太陽的時角。

三者可通過查詢天文歷獲得，太陽矢量在p 系中可表示為：

根據模型可得到 m 系下理論最大偏振矢量 E′的表達式：

式中： [W m ×]為觀測矢量的反對稱矩陣; Cb m 為載體坐標系到偏振光測量坐標系的轉換矩陣; Cnb Q 為四元數表示的導航坐標系到載體坐標系的轉換矩陣; Cp n 為太陽坐標系到偏振光測量坐標系的轉換矩陣。

本文中，偏振光傳感器輸出值為最大偏振矢量與偏振光傳感器參考軸的夾角α，忽略偏振光傳感器輸出誤差，偏振光傳感器實測偏振矢量可以表示為：

2 基于偏振模式的組合導航航姿最優化方法求解

共軛梯度法是求解大型非線性無約束優化問題最常用的算法之一，通常以迭代點處的負梯度方向與共軛方向的線性組合來確定較優搜索方向，通過迭代逐漸逼近最優解[14-15]。本文利用加速度計傳感器，偏振光傳感器實測數據與理論數據的誤差構建目標誤差函數模型，并通過求解誤差函數最小值，獲得偏振光輔助航姿解算系統的最優姿態四元數，進而得到最優航姿姿態估計值。

2.1 重力矢量誤差函數模型

參考1.2節中的偏振光理論測量坐標系模型，單位重力矢量在導航坐標系中為：

將重力矢量轉換到載體坐標系下：

式中： Ag（b）（Q ）為載體坐標系中四元數表示的理論重力矢量;? Cnb （Q ）為四元數表示的導航坐標系到載體坐標系的轉換矩陣。

在靜止與飛行中，MEMS加速度計傳感器輸出量可以認為是重力在載體坐標系中的投影，加速度計輸出量為：

式中： abx 、 ay（b）、? abz 為加速計三軸輸出量。

載體坐標系中，加速度計的輸出量與理論重力矢量的差值反應的而是姿態矩陣估計的誤差值，因此建立重力矢量誤差模型：

對四元數 Q =q0?? q 1?? q2?? q3T 求微分得到重力矢量誤差模型的 Jacobian矩陣 Jεb Q ：

2.2 偏振矢量誤差函數模型

參考1.2節中的偏振光理論測量坐標系模型，查詢天文年歷和經緯度信息，根據偏振矢量與太陽矢量及觀測矢量組成的平面成垂直關系，由式（15）得到四元數表示的偏振光測量坐標系下的理論偏振矢量 Esm Q ：

式中： vx（n）、? vy（n）、? vz（n）為太陽矢量Vs p 在導航坐標系下投影 Vs n 的三軸分量。

偏振光傳感器的輸出量為偏振光測量坐標系中偏振矢量與傳感器參考軸的夾角，測量偏振矢量可表示為：

由理論偏振矢量與測量偏振矢量可得到偏振矢量誤差模型：

對四元數 Q =q0?? q 1?? q2?? q3T 求微分得到重力矢量誤差模型的 Jacobian矩陣 Jεm Q ：

2.3 動態步長因子設計

根據2.1節中建立的重力矢量誤差模型 AbεQ 及其對應的 Jacobian矩陣 Jεb Q ，2.2節中建立的偏振矢量誤差模型 Eεm Q 及其對應的 Jacobian 矩陣 Jεb Q ，組建偏振光輔助航姿解算系統的綜合矢量誤差模型 F Q 及其對應的 Jacobian矩陣 J Q ：

由無約束優化方法中的梯度優化理論，得到綜合矢量誤差函數的梯度：

為減小計算量，定義步長為：

式中：k 為姿態四元數第 k 次迭代;?F Q k 為第 k 次迭代的梯度; Dk Q 為第 k 次迭代的搜索方向，以負梯度方向-?F Q k 與黑塞矩陣的近似矩陣 Bk Q 通過線性組合得到。

規定搜索方向：

其中， Bk Q 通過 BFGS修正公式獲得：

根據載體的運動狀態變化引入動態步長因子，當姿態變化較小時，動態步長因子減小，反之，動態步長因子增大，提高解算精度，加快收斂速度，動態步長因子αk?? （可變化）定義為：

式中： Q?k 為第 k 次迭代的四元數微分，通常共軛梯度優化方法需通過多次迭代來獲得最優解，但在航姿求解中，每一次迭代都可以得到姿態四元數的最優解。

由于重力加速度計輸出為重力加速度與運動加速度的矢量和，當運動加速度過大時會影響模型解算精度，因此設計狀態閾值 c ，當加速度計輸出大于設定值ε時，運動加速度較大應減小搜索步長，提高搜索精度。

本方法通過求解綜合姿態矢量誤差函數最小值，求解最優四元數，對陀螺儀數據進行補償，完成最優姿態四元數的解算，過程如下：

式中： ω b =ωbx?? ωy（b）? ωbz為陀螺儀測得的角速度矢量;?為四元數乘法運算; ΔT 為姿態四元數更新周期; P Q k 為最優搜素方向。

3 實驗驗證與結果分析

基于偏振光輔助的航姿解算系統主要包括慣性測量單元與偏振光傳感器。本實驗使用 Paparazzi uav開源項目中 Lisa/M2.0飛控系統（集成慣性測量單元MPU6000和地磁傳感器 HMC5883L）中慣性測量傳感器輸出數據與偏振光傳感器輸出數據進行數據融合估計姿態并將飛控系統輸出作為實驗參考值，該系統使用慣性測量單元與地磁傳感器作為姿態估計傳感器，圖 3所示為飛控系統輸出精度測試結果。

考慮到飛控板安裝誤差的存在可以認定飛控系統輸出具有一定精度可以作為參考值。為了評估提出的航姿解算方法，分別在靜態與動態實驗環境下進行實驗驗證，并與飛控系統實驗參考值，梯度下降優化法與共軛梯度優化法進行對比分析，以驗證本文中基于動態步長因子與狀態閾值的擬牛頓優化航姿解算算法的可靠性和準確性。

3.1 靜態實驗測試及分析

靜態實驗地點為大連理工大學機械東樓樓頂（121.528255° E ，38.8814192° N），海拔35 m ，時間是2021年1月17日上午10：34，天氣晴朗，根據天文歷表可知太陽高度角為26.12°，太陽方位角為-0.8°。由于將實驗平臺靜止放置在地面一段時間，實驗數據如圖4所示。圖中展示了靜態實驗中本文設計的基于動態步長因子的擬牛頓優化方法與梯度下降法、共軛梯度法的姿態對比曲線和狀態變化曲線。圖中狀態變化曲線平緩，符合靜態實驗的特點。

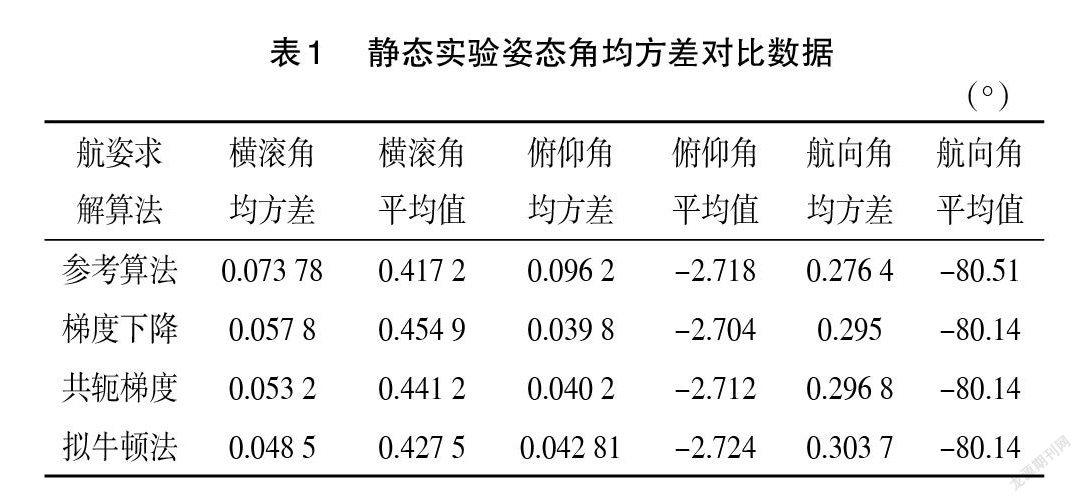
為進一步說明不同方法之間的差異，表1所示為靜態實驗姿態角均方差以及平均值對比數據。由表可知，橫滾角中，擬牛頓法最接近參考值，俯仰角中，共軛梯度法與擬牛頓法最接近參考值，誤差相同，航向角中，3種優化方法平均值相同，可以看出3種優化方法在靜態時沒有明顯區別。與參考值相比較，在可接受誤差范圍內，具有一定靜態精度與穩定性。

3.2 動態實驗測試及分析

選取地點不變，時間是2021年1月16日16：33，根據天文歷表可知太陽高度角為2.64°，太陽方位角為-143.16°。將偏振光導航實驗平臺在三維空間中，實驗數據如圖5所示。由圖可知，在姿態變化時，本文的擬牛頓優化方法可以很好地跟蹤姿態角的變化。狀態變化的曲線，符合實驗的動態特點，對復雜運動狀態下的姿態誤差起到了調控作用。

為了更直觀地比較姿態解算方法的差異，圖 6所示為不同方法獲得的姿態角的偏差曲線圖。由圖可知，在姿態變化時，基于動態步長因子與狀態閾值的擬牛頓優化方法的收斂速度快于其他方法，姿態估計角度誤差較小。

為進一步說明其他方法之間的差異，表2～3所示為動態實驗姿態角最大絕對值誤差以及誤差均方差對比數據。由表可知，基于動態步長因子與狀態閾值的擬牛頓優化航姿解算的姿態角誤差最小，較梯度下降法精度提高50%，較共軛梯度法精度提高37%～50%，說明基于動態步長因子的共軛梯度法與其他方法相比，在誤差最小的情況下誤差波動最小，表現出更好的動態收斂性，動態精度更高，驗證了對于偏振光輔助的捷聯慣導導航系統共軛梯度優化方法有利于飛控系統的航姿估計。

4 結束語

本文將點源式偏振光傳感器引入傳統慣導系統替代磁強計，構成新的航姿參考系統（陀螺儀、加速度計、偏振光傳感器），利用誤差最小原理搭建算法模型，通過動態步長因子優化的擬牛頓法進行最優解求解，通過狀態閾值抑制運動加速度對加速度計的干擾，實現姿態解算，為偏振光導航提供了一種新的航姿求解方案。實驗結果表明，擬牛頓優化的航姿解算方法在靜態環境下的具有一定精度與平穩性，而且由于動態步長因子與狀態閾值的設計，在動態環境下也表現出較好的姿態跟蹤能力，與梯度下降法、共軛梯度優化的濾波算法的對比結果表明，擬牛頓優化方法的解算收斂速度更快，姿態誤差更小，說明本文提出的偏振光/慣導組合導航的擬牛頓優化航姿算法能夠有效提高偏振光輔助導航系統的姿態跟蹤能力與解算效率。

在建立重力矢量模型時，忽略了運動加速度對加速度計輸出的影響，雖然使用狀態閾值進行抑制，并且優化搜索本身基于誤差最小情況進行，但在運動加速度過大時仍會影響姿態解算，下一步工作將考慮建立運動加速度計誤差補償，從而進一步優化現有姿態解算模型，以提高偏振光/慣導組合導航系統的魯棒性能。

參考文獻： [1] 褚金奎， 王洪青， 戎成功. 基于偏振光傳感器的導航系統實驗測試[J]. 宇航學報， 2011， 32（3）：489-494.

[2] Chahl J ， Mizutani A . Biomimetic Attitude and Orientation Sen? sors[J]. Sensors Journal， IEEE， 2012， 12（2）：289-297.

[3] W Stürzl， Carey N. A Fisheye Camera System for Polarisation Detection on UAVs[C]//European Conference on Computer Vi? sion， 2012.

[4] D Wang， H Liang， H Zhu. A bionic camera-based polarization navigation sensor[J]. Sensors，2014，14（7）：13006-13023.

[5] Huang H， Yang Z， Zhou J. Microsatellite attitude determination based on skylight polarization and geomagnetic measurement[J]. Optik-International Journal for Light and Electron Optics， 2018 （178）：1177-1184.

[6] 褚金奎， 林木音， 王寅龍，等. 偏振光傳感器的無人船導航與編隊應用[J]. 光學精密工程， 2020（8）：1661-1669.

[7] 曾云豪，杜濤，星艷.基于慣性/偏振光/光流的六足步行機器人自主導航方法研究[J]. 導航定位與授時， 2020，39（6）：108-114.

[8] He X， Zhang L， Fan C， et al. A MIMU/Polarized Camera/GNSS Integrated Navigation Algorithm for UAV Application[C]// 2019 DGON Inertial Sensors and Systems （ISS）. IEEE， 2019.

[9] 金仁成，陳文，孫會生，等. MIMU/偏振光互補濾波組合導航算法研究[J].燕山大學學報，2016， 40（3）：276-282.

[10] Qian H， Qiu Z. Iterated Unscented Kalman Filter for Spacecraft Attitude Estimation[C]//中國控制會議，2018.

[11] Feng L， Yue B， Qu X. Airborne platform estimation based on the algorithm of Unscented Kalman filter quaternion[C]//2016 IEEE Chinese Guidance， Navigation and Control Conference （CGNCC）. IEEE， 2017.

[12] 陳國通， 范圓圓， 孫敬. 四元數算法在姿態矩陣解算中的研究[J]. 信息通信， 2019（3）：46-48.

[13] 金仁成， 孫加亮， 謝林達，等. 基于偏振光傳感器的全姿態角解算方法研究[J]. 單片機與嵌入式系統應用， 2018（6）：47-50.

[14] 孫金秋，游有鵬，傅忠云.基于共軛梯度法和互補濾波相結合的姿態解算算法[J].傳感技術學報，2014，27（4）：524-528.

[15] 曾聰，章政，王龍.基于共軛梯度的EKF姿態估計算法[J].計算機工程與設計，2018，39（10：）3118-3128.

第一作者簡介：金仁成（1969-），男，吉林長春人，博士，副教授，研究領域為無線傳感器網絡與無人機自主導航技術，已發表論文70余篇。

（編輯：王智圣）