基于IR-UWB 信號特征匹配的空間TDOA 系統的設計及LOS 環境下的誤差分析
李 虎,高 路,白錦良,劉佳琪,孫 恒
(北京航天長征飛行器研究所,北京,100076)
0 引 言
當前再入飛行技術日新月異,為了滿足對位置服務的需求,各種定位技術不斷發展。其中空間目標定位作為最常見的定位應用,一直受到業界的重視。由于空間目標定位系統有著自身的特點,需要結合具體情況進行分析和設計,并不能完全照搬一些定位技術。實用的空間目標定位技術至少滿足以下條件:a)抗干擾能力強;b)生產成本低;c)系統功耗低;d)收發器體積小。目前,常見的目標定位技術包括有GPS 輔助(A-GPS)技術、射頻識別技術(Radio Frequency Identification,RFID)、無線局域網(Wireless LAN,WLAN)和沖激無線電-超寬帶(Impulse Radio-Ultra Wideband,IR-UWB)技術等[1,2]。
其中,IR-UWB 技術具有以下優點:a)IR-UWB信號無載波,不需要調制解調,所以收發系統簡單,生產成本低;b)IR-UWB 信號為納秒或亞納秒級別的窄脈沖,時間分辨率非常高,平均功率較低。所以,IR-UWB 技術結合基于到達時間的測距技術(例如時差定位)能夠充分利用時間分辨率高的特點[3],特別適合定位系統,在近幾年得到了廣泛的研究[4,5]。
對于定位系統來說,其定位誤差分析都是系統設計中的關鍵部分。時差定位(Time Difference of Arrival,TDOA)方法廣泛應用于地面與空間等定位系統中,系統組成的探測網絡由若干接收器組成,系統通過處理多個測量站采集到的信號到達時間數據對IR-UWB 的發射器進行定位。發射器發出的IR-UWB 信號到達任意2 個接收器的時間的差值確定了一對以2 個接收器為焦點的雙曲面,為了獲得發射器的三維坐標,需要至少4 個接收器產生3 對雙曲面,交匯解出輻射源的位置。在發射器某一坐標信息(如高度信息)可提前預知的情況下,采用3 個接收器或更少接收器測量也可以求得發射器的三維坐標。對于TDOA 系統的誤差分析采用類似文獻[6]的技術手段,其噪聲建模為單一的高斯白噪聲(本文中稱為“總體時差噪聲”)。但是在實際系統中,在系統的不同部分存在不同類型的噪聲,用單一的高斯白噪聲直接建模過于粗略,對系統設計的指導意義不夠明確。本文通過對實際系統的分析,將在工程中對實際系統精度影響較大的3 種誤差(位置誤差、時差量測誤差、時間同步誤差)進行建模并分析,得到他們與定位精度的數量關系并進行仿真,以便指導實際系統的設計。
1 定位模型
基于IR-UWB 信號特征匹配的TDOA 系統分為發射器、接收器和位置解算器3 個部分,以坐標軸建立笛卡爾坐標后,系統結構如圖1 所示[7]。
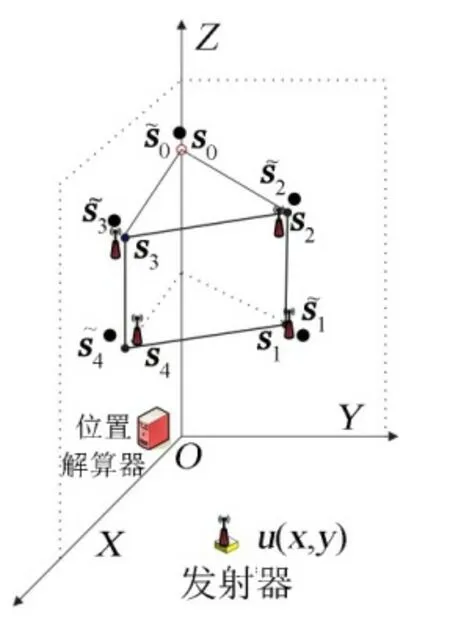
圖1 系統結構示意Fig.1 System Configuration
系統中的M個發射器位于地面,間斷的循環發射IR-UWB 信號,不同發射器的IR-UWB 信號的特征不同。系統中的N個接收器(編號分別為 0,1,...,N-1)位于空間,用于接收發射器發出的無線信號,其位置已知且固定。接收器的真實位置記作si=[xi,yi,zi]T,由于誤差影響,得到的接收器的位置記作is~ 。其中1個接收器作為主站(位置為s0),其他N-1 個接收器用作副站。主站和副站的區別在于主站具有時間模塊,副站用有線方式通過主站獲得時間。只在主站中放置時鐘模塊的原因:一是為了減少模塊個數,可以節省成本;二是TDOA 系統是靠時間差來定位的,如果副站也放置時鐘模塊,對時鐘模塊的同步要求比較高,只采用1 個時鐘模塊無需同步,節省成本。
發射器和接收器之間通過無線進行信號傳輸,接收器和位置解算器之間通過有線方式傳遞信息。主站和副站利用特征匹配的定位算法[8,9],根據IR-UWB 信號的特征與發射器的特征進行匹配,并將識別結果(包括發射源編號和到達時間(Time of Arrival,TOA))通過有線傳輸方式傳送給信號處理器。信號處理器綜合主站和N-1 個副站給出的識別結果,利用TDOA 算法解算出各發射器位置。信號處理流程如圖2 所示。
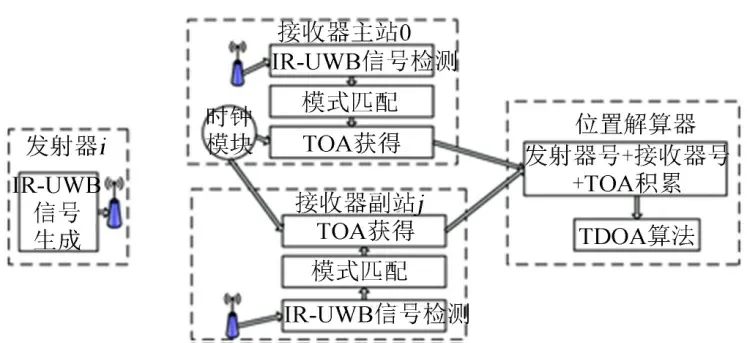
圖2 信號流程Fig.2 Signal Processing
2 誤差分析
本節分析在第1 節中設計的TDOA 系統的定位精度和誤差的關系。只考慮了視距(Line of Sight,LOS)環境下的結果,對于超視距環境(主要考慮陰影效應和多徑效應)下的精度只會更差。從這個角度看,給出的結論是定位精度的一個上界。第1 節中給出的系統在工程中常見的誤差包括站間時間同步誤差、到達時間量測誤差和位置誤差。定位誤差與總體時差誤差、觀測站和目標相對位置有關,可以分為直接時差誤差和間接時差誤差。直接時差誤差包括時間同步誤差、時差量測誤差;間接時差誤差主要由觀測站的位置誤差引起。由前文可知影響精度的主要因素包括:站構型(包括基線長度)、站間時鐘同步精度、自定位精度、對脈沖到達時間的測量精度,這些因素與精度之間定性的關系如表1 所示。在本節進行定量分析,上述因素都可轉化為“總體時差誤差”進行統一分析。

表1 系統誤差影響因素分析Tab.1 Analysis of System Error
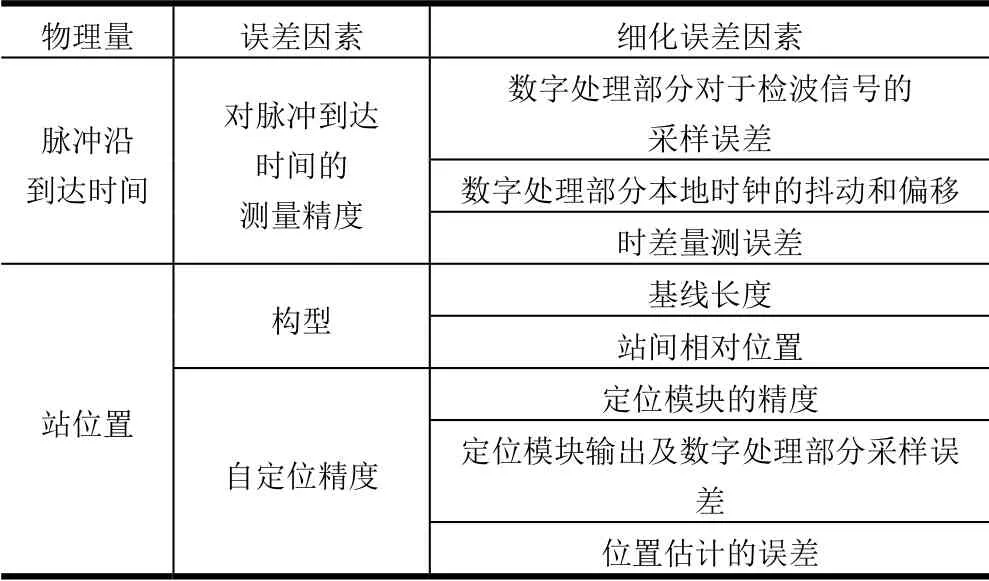
續表1
站間時間同步誤差是指2 個接收器時間同步引起的誤差,用Δtsys表示,可假定為方差為的高斯白噪聲。到達時間量測誤差與時差測量方法有關,可假定為方差為的高斯白噪聲。位置噪聲由接收器自身位置誤差引起,包括接收器在x,y,z3 個方向上的誤差,用Δs表示。下面分析中假定位置測量誤差各向同性,建模為協方差陣為的白高斯隨機矩陣,I為3 × 3的單位陣,σs為接收器位置誤差半徑平方的均值。
分析誤差分量與總體時差噪聲的關系。由圖1 可知,以主站和副站1 為例,研究接收器位置誤差、站間時間同步誤差和到達時間量測誤差對時差測量精度的影響。假定發射器位于u=[x,y]T處,于t0時刻發射了1 個脈沖,主站和副站1 在s0和s1處接收到信號的時間分別為tr0,tr1:
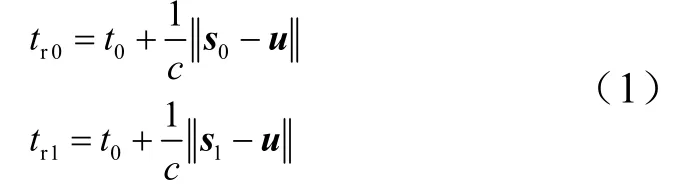
式中c為光速;主站測得的到達時間tr0的實際測量值為trm0:

式中 Δt0為主站的時間量測誤差,假定它是服從均值為0、方差為的高斯分布的隨機變量。副站1 測得的到達時間tr1的實際測量值為trm1:
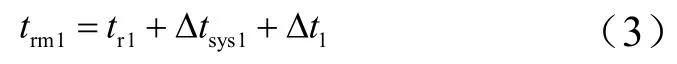
式中 Δtsys1為副站1 與主站的時間同步誤差,假定服從均值為0、方差為的高斯分布;Δt1為副站1 的時間量測誤差,假定它是服從均值為0、方差為的高斯分布的隨機變量。
由于接收器的真實位置不能確定,只能得到含有誤差的主站和副站1 的坐標矢量和:
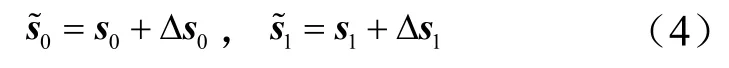
即:

式中 Δs0和Δs1分別為主站和副站1 的位置測量誤差。
就單個時差量測值τm1=trm1-trm0而言,有:

上式只含有未知的位置參數,其余參數是已知的。式(8)中 Δτ1為總的時差測量誤差,表達式為式(9)。
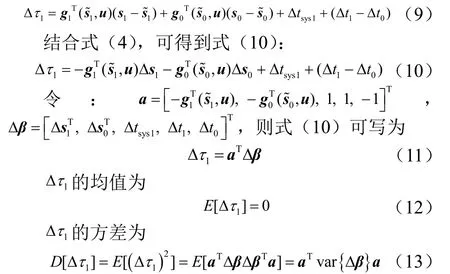
假定接收器位置測量誤差、時間同步誤差、時間量測誤差之間相互獨立,則Δβ的協方差矩陣可表示為式(14)。將式(14)代入式(13),可得式(15):
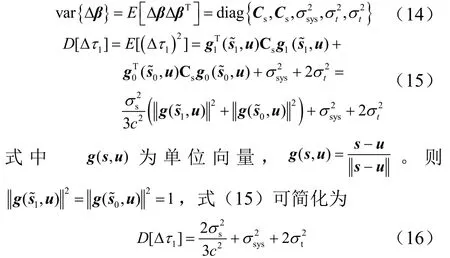
由式(16)可知,總體時差誤差的方差D[ Δτ1]與接收器位置誤差、站間時間同步誤差以及到達時間量測誤差有關,而與接收器的位置和發射器的位置無關。
總體時差誤差的均方根誤差 1τσ為
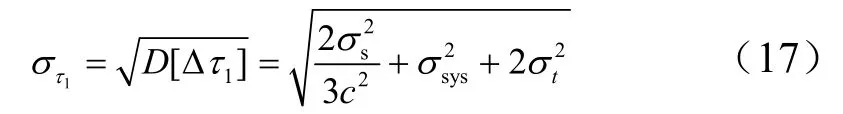
式(17)的直觀意義為:時差量測誤差對于時差的影響是雙重的,所以其方差的因子為2;位置誤差對于時差的影響需要乘以光速的倒數轉換為時間,并且也是雙重影響,所以其方差的因子為22;時間同步誤差是各個副站對于主站的誤差,其方差的因子為1。
結合文獻[3]的結論,協方差矩陣Pu為

由式(18)可知,除了上述3 種誤差對于CEP 有影響之外,布站也會通過影響矩陣H來影響精度。
根據協方差矩陣Pu也可以確定定位誤差橢圓關于x,y的方程為
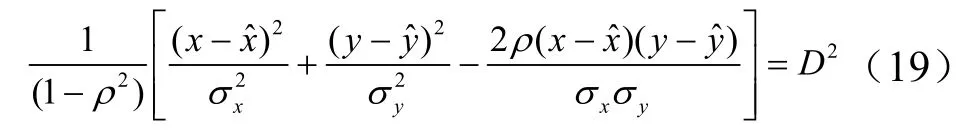
式中ρ為協方差矩陣中系數;D2=-2 ln(1 -P);通常將P=0.5所對應的橢圓稱為橢圓概率誤差,此時D= 1.1774;為目標位置估計值。定位誤差橢圓的參數包括半長軸a、半短軸b和長軸方向θ。當ρ=0時,式(19)變為
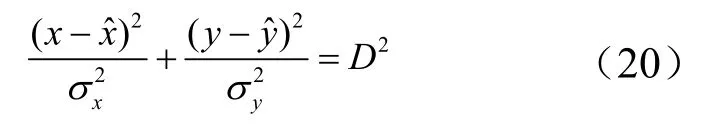
根據σ x,σy可直觀得到定位誤差橢圓的參數:
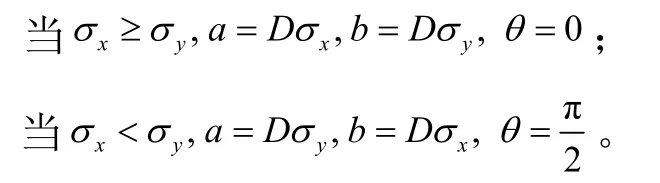
當ρ≠ 0時,作坐標變換:
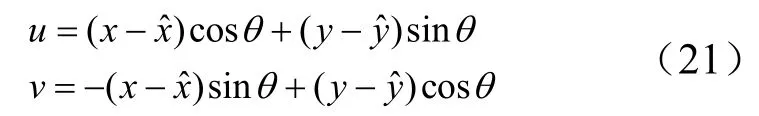
式中u,v為新坐標系中坐標變量;定位誤差橢圓在新坐標系下的表達式變為

3 數值仿真
對于圖1 中的系統,按照上述分析的結論進行精度的仿真。
首先分析總體時差誤差各因素的影響關系。當位置誤差和時間同步誤差固定時,時差量測誤差隨時間測量誤差的變化關系如圖3 所示。由圖3 可知,總體時差誤差隨著時間量測誤差的增大而增大,當時間量測誤差較小時,觀測站位置誤差和時間同步誤差主要影響總體時差誤差,當時間量測誤差較大時,時間量測誤差對總體時差誤差的影響較大。
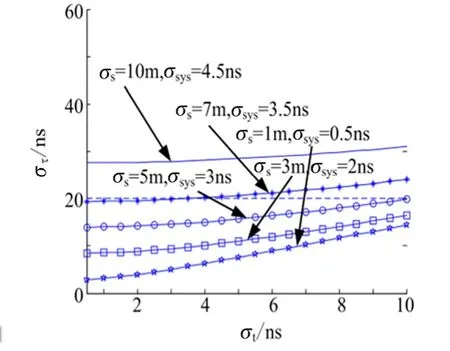
圖3 總時差誤差隨與時間測量誤差的變化關系Fig.3 Total TDOA Error v.s.Time Measurement Error
當位置誤差和時間量測誤差固定時,總體時差誤差隨時間同步誤差的變化關系如圖4 所示。由圖4 可知,總體時差誤差對時間同步誤差不敏感,即當觀測站位置誤差和時間量測誤差確定后,提高時間同步精度對提高時差測量精度貢獻并不大。
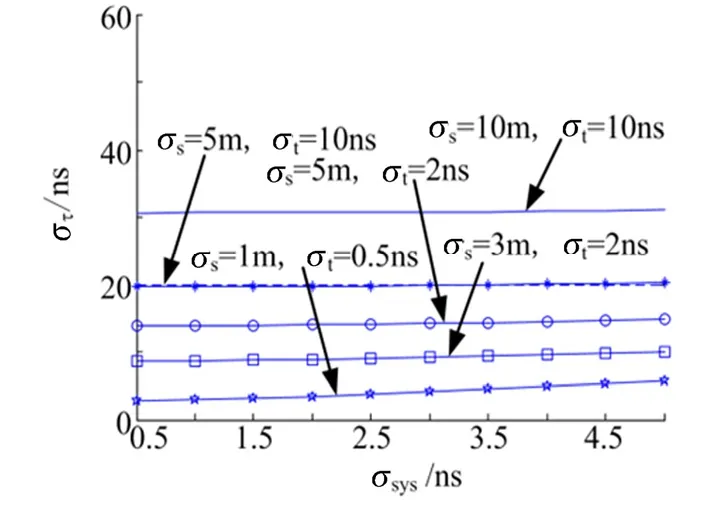
圖4 時差測量誤差隨時間同步誤差的變化關系Fig.4 TDOA Error v.s.Time Synchronization Error
仿真假設接收器數量為5 個,其中主站坐標為[0,0,3],4 個副站的坐標分別為:[2,0,2]、[2.5,0,2]、[0,2,2]、[0,2.5,2](上述坐標中數值單位均為km)。
當接收器位置誤差為0.01 m,時間同步誤差為3 ns,時間量測誤差為2 ns 時,仿真結果如圖5a 所示;當接收器位置誤差為0.1 m,時間同步誤差為4 ns,時間量測誤差為8 ns 時,仿真結果如圖5b 所示。
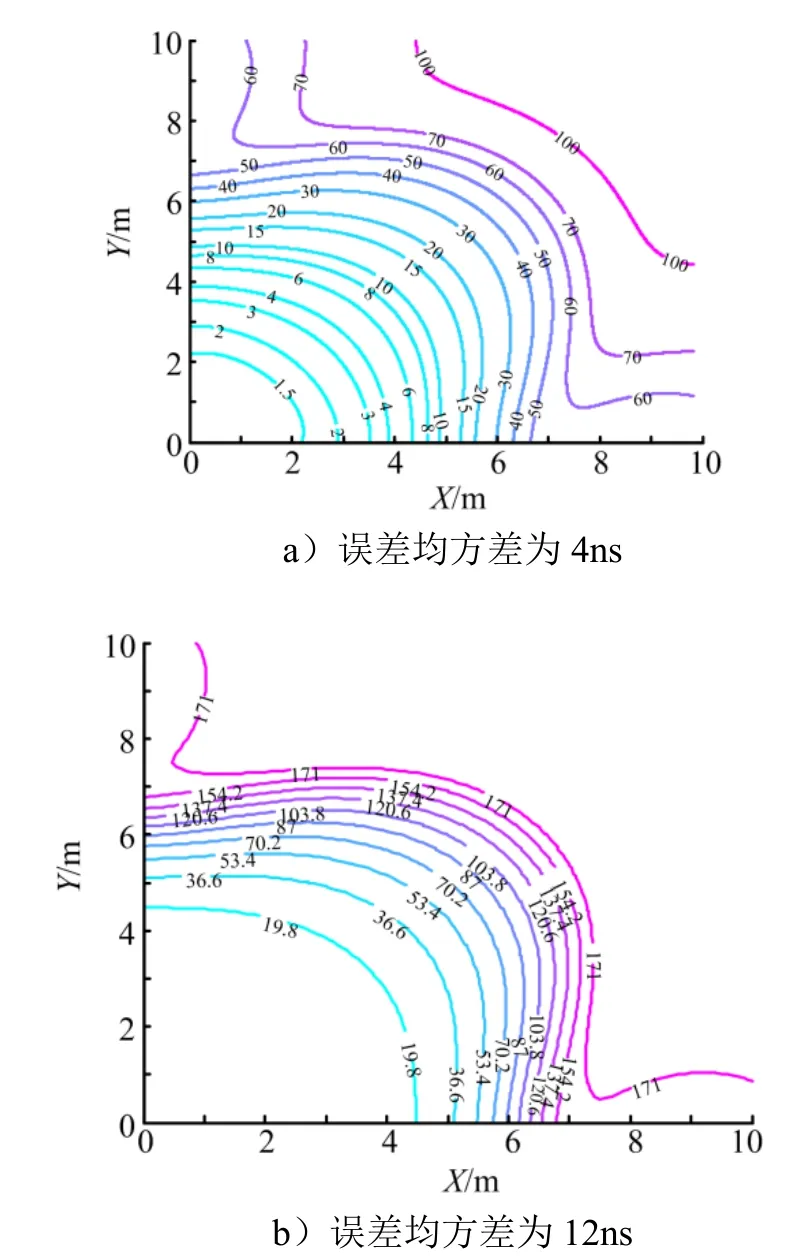
圖5 不同系統誤差下系統的精度CEP 分布Fig.5 CEP v.s.System Error
從圖5 可以看出,距離接收器越遠的位置,定位精度越差。此外還可以看出,系統中的誤差指標越差,會導致定位精度的惡化。需要結合具體系統指標對站址布局等因素進行合理優化。
4 結 論
本文給出了基于IR-UWB 信號特征匹配的TDOA系統的原型和初步設計,并且對于LOS 環境下,針對實際系統設計過程中最常見也是對精度有直接而重要影響的3 類誤差:位置誤差、時差量測誤差、時間同步誤差,進行了分析,得到了其與總時差誤差的數量關系。最后對1 個實例系統進行了CEP 仿真,得到上述誤差對于系統精度影響的直觀概念。在實際系統設計中,應當根據系統的經費預算和各個分系統的性能指標合理進行參數分配。并應針對房屋的不同結構,選擇不同的接收站結構布局設計,以便在允許的經費范圍之內實現對重要區域達到比較高的精度。

