云數據技術背景下地理信息系統與大數據的技術分析

李薇

（沈陽市勘察測繪研究院有限公司，遼寧 沈陽 110004）

1 GIS 大數據耦合技術分析

公式（1）中分類器T 為真實，其中分類誤差率P 屬于未知數，而在GIS 大數據耦合數據的驗證中通常將樣本集D 內的任一樣本進行刪除，并且不會對T 的泛化誤差產生任何的影響。

通常樣本集D 內的樣本數量是一定的，因此T 及D 將無法達到相互獨立存在的形式，由此，通過對模型預測性的實施評價后，若是能夠將交叉驗證評價所獲得的泛化誤差率作為模型計算中的真實誤差率，那么將會產生較高的誤差值，而此誤差數值可通過置信區間進行評價[3]。

式中：Za/2 為在分割標準正態分布過程中獲取的右邊尾部面積的a/2 處分割位置的Z 值；W 為置信區間的寬度。

通過上述的計算驗證可以確定，依據大數據增益的原理能夠反真實的的評估、反饋出評估準則的可行性，并且對精確率及召回率具有更好的評估能力，但是相對而言準確率卻稍差；另外，由于在進行GIS 與大數據的耦合后將會產生更大范圍的增益應用范圍，但置于F 測量準則可更加適合不平衡比例的樣本數據集[4]。

2 云數據技術計算過程

在正常狀態狀態下，隨著樣本數m 的逐漸增大，GIS 大數據分析技術驗證置信度也隨之上升，不過這一正相關關系并不是無限制的。研究發現，若僅僅只是對m 進行單純的增加，則容易造成交叉驗證的漸進出現較大偏差。由此可見，若保證有效性，則要增加D 與T 的獨立性[5]。

假設x1，x2，…，xk是第1 組樣本，表示模型X 在不同數據集上的估計值，假設y1，y2，…，yk是第2 組樣本，表示模型Y 在不同數據集上的估計值，x1與y1相互配對，二者是采用相同的數據而產生的樣本，x2與y2相互配對，二者是采用相同的數據而產生的樣本，x3與y3也是如此，按照這樣的配對方式，直到最后一個樣本。用μ1來表示是第1 組樣本的平均值，用μ2來表示是第2 組樣本的平均值。有了平均值之后，若對兩個模型進行比較，則直接看平均值是否有顯著的差別。兩個實驗模型在實驗的過程中進行了一定的配對，故而也稱為配對的云數據技術測試。表1 所示為在樣板本比較少的情況下所進行的配對云數據技術檢驗方法。

表1 小樣本情況下配對云數據技術檢驗方法

定義4 給定分類模型f1與f2，若IG（f1）＞IG（f2），則對于不確定性的減少，f1比f2更有優勢。

常常采用4 種模型對云數據技術問題進行解決，第1 種模型是準確率；第2 種模型是精確率；第3 種模型是召回率（Recall）；第4 種模型是F 測量。

在yes 與no 二分類過程中，同一模型將會得到4 種不同結果，依次對應為正確的肯定（true positive，TP）、正確的否定（true negative，TN）、錯誤的肯定（false positive，FP）、錯誤的否定（false negative，FN）。

準確率、精確率、召回率和F 測量的計算可以采用如下公式。準確率：

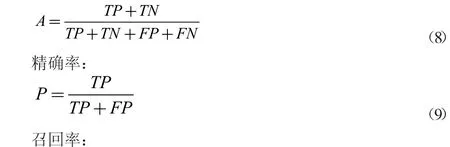
對于一些更為綜合的模型，其預測性能的評估指標就可以采用大數據增益，從本質上來說，大數據增益類似于非線性的方式，它以這種非線性的方式對各種準則進行相應的平衡，因此采用大數據增益進行評估，可以得出其他相關的大數據，具體如下。

（1）根據大數據增益的原理，可以對有關評估準則具備的實際評估能力進行一定程反映。尤其是依據精確率和召回率，可以發現更多的大數據。相對來說，精確率和召回率的評估能力更強，準確率則相對較弱[6]。

（2）相比之下，大數據增益準則的使用范圍更寬。對于采用F 測量準則的情況，其比較適用于具有不平衡比例的樣本數據集。

3 結論

隨著經濟全球化的推進及其GIS 大數據危機在世界范圍內的影響，關于GIS 大數據分析技術，得到了越來越多的專家關注，同時也已經成為GIS 大數據核心內容之一，關于GIS 大數據分析技術，在國際上并沒有形成統一的標準，很多人在對實際問題進行解決的時候，往往只是憑借自己的主觀經驗或者以往經驗，通過經驗來解決實際問題，往往會出現較大的盲目性，鑒于此，有效利用科學技術，對云數據技術創新能力培養的準則與方法采用科學的模型進行解決勢在必行。

基于這樣的背景，本文在GIS 大數據分析技術與應用中引入了糾正重復取樣云數據技術測試的云數據技術，通過專業的方法，提出了基于云數據技術的GIS 大數據分析技術，通過實驗研究表明，從云數據技術中可以發現一些規律，若采用的規則矩陣不同，則結果也不同。