類橢球體放礦理論移動過渡方程的研究

李金河 范才兵 郭進平

（1.中鋼礦業豐寧萬隆礦業發展有限公司；2.中鋼礦業開發有限公司；3.西安建筑科技大學資源工程學院）

類橢球體放礦理論是在實驗觀察、回歸分析和理論研究的基礎上創立的，其包含了橢球體放礦理論的部分合理內核（如移動跡線方程、移動過渡方程、相關關系方程），解決了橢球體放礦理論存在的問題和不足（如放出體形、移動邊界、速度場和密度場）［1］，拓展和發展了橢球體放礦理論。

移動過渡方程是放礦理論的重要基礎方程，是評價一種放礦理論是否正確、完備的重要指標［2］。為夯實理論基礎，特對類橢球體放礦理論的移動過渡方程建立的基礎以及建立過程進行深入研究。

1 移動過渡方程建立的基礎

類橢球體放礦理論的移動過渡方程是建立在移動過渡原理和質量守恒定律的基礎上的。

1.1 移動過渡原理

移動過渡原理是放礦理論最重要的基礎。前蘇聯學者Г.М.馬拉霍夫根據實驗認為，放礦中存在放出體過渡和等速體（等速度面）過渡，并根據等速度體過渡建立了橢球體放礦理論［3］。前蘇聯學者B.B.庫里柯夫根據實驗認為，放礦過程中只存在放出體過渡，并在放出體過渡的基礎上，建立了現行的橢球體放礦理論。許多研究者通過實驗證實了B.B.庫里柯夫的觀點是正確的。因此，移動過渡原理被準確描述為放出體移動過渡原理。

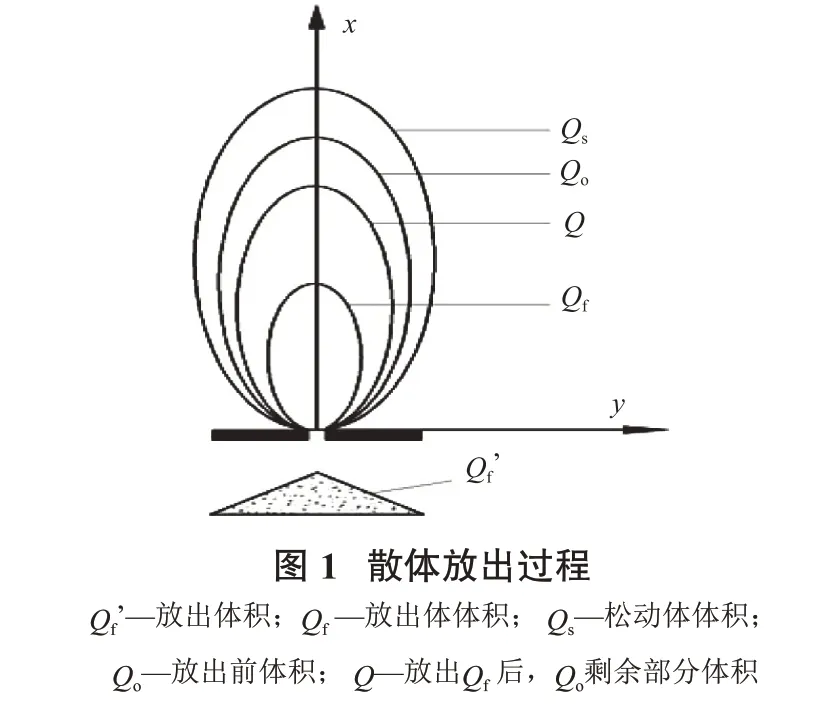
如圖1所示，設Q0空間中的散體顆粒放出放出體Qf后移動到Q（即Q0中未放出的散體占據空間位置Q），這種移動過渡關系包括以下內容：

（1）整體過渡。即Q0內所有散體，除放出體Qf內的顆粒已放出，其余全部散體顆粒都移動到了Q內。

（2）移動體表面整體過渡。即Q0表面那些顆粒都移動到了Q表面上。

（3）顆粒間相關位置不變化的整體過渡。即顆粒間位置不互換，顆粒順次移動（位置坐標比例不變）。

（4）體形不變整體過渡。即類橢球體的體形不變，決定體形的參數不變。

1.2 質量守恒定律

質量守恒定律是建立移動過渡方程的基礎，對于散體場應用質量守恒定律的條件為

（1）散體場為無源場，即散體場中無其他散體源；

（2）散體場底部的放出口是唯一的，散體場中無任何其他放出口。

2 理想散體的移動過渡方程

研究散體放出過程中的質量變化，根據質量守恒定律，可建立散體移動過渡方程的質量平衡方程如下。

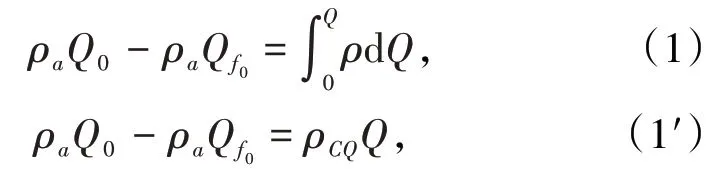
式（1）、式（1′）對于理想散體和實際散體均適用。式中，Q0為散體放出前的散體體積；Qf為散體放出體體積；Q為放出Qf時，中Q0剩余散體顆粒在散體場中的散體體積；ρ為散體移動范圍內的密度；ρa為散體放出前的初始密度；ρCQ為放出散體Qf時，Q中散體的平均密度。

對于理想散體有二次松散系數η=1，散體密度場為均勻場和定常場，即散體放出前及散體場中各處密度均相等，且不隨時間變化。同時，由于無二次松散現象，因此當散體放出開始時，散體場中移動范圍內的所有散體顆粒都同時開始移動，無移動滯后現象。故有

式（2）代入式（1′），整理變換得：

式（3）即為類橢球體放礦理論理想散體的移動過渡方程［4］。

3 實際散體質量平衡狀態分析

對于實際散體，有二次松散系數η＞1，散體密度場在放出前為均勻場和定常場。在放出開始后的放出過程中，由于二次松散使移動范圍內各處的密度隨坐標位置及時間而變化，移動范圍內的密度場為非均勻場和不定常場，但移動范圍之外密度仍然保持不變，為均勻場和定常場。

可根據Q0表面顆粒的狀態劃分出實際散體不同的質量平衡狀態。

3.1 Q0表面顆粒靜止不動（靜止狀態）

當放出體Qf＜Q0C時，此時Qs＜Q0，其質量平衡方程為

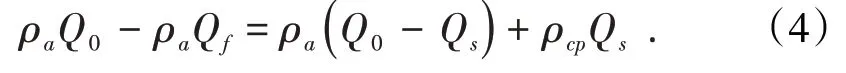
整理得到：

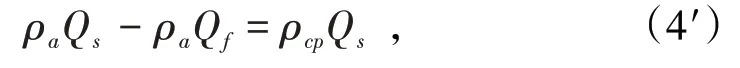
式中，Qs為對應于放出體Qf的松動體體積；C為松動范圍系數，；ρcp為松動體Qs內的平均密度，ρcp=ρaη［6］。

式（4′）為Qf＜Q0C時的質量平衡方程。

由式（4′）可知，此時Q0表面顆粒靜止不動，Q0與Q、Qf不存在函數關系。

3.2 Q0表面顆粒即將投入運動（臨界狀態）

當放出體Qf0=Q0C時，此時Q0=Qs=Q，Q0表面顆粒正處于松動體邊界上，雖然靜止不動，但即將投入運動，處于臨界狀態，此時質量平衡方程為

或

當Q=Qs=Q0時，有ρCQ=ρCP，故由（1）式得：

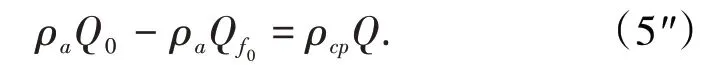
式（5）、式（5′）、式（5"）為Q0表面顆粒處于臨界狀態（靜止但即將投入運動）的質量平衡方程。

3.3 Q0表面顆粒投入運動

當放出體Qf＞Q0C時，此時Qs＞Q0，因此Q0表面顆粒在移動范圍內向下移動。此時的質量平衡方程為（1）式或（1′）式。

將式（5′）代入式（1）或式（1′）得：

整理得：

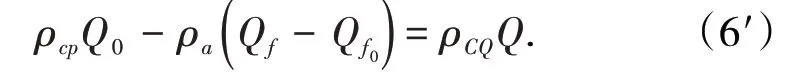
式（6）或式（6’）也為Q0表面顆粒投入運動（移動狀態）后的質量平衡方程，式（6）實際是式（1）的另一種表達形式。由式（6′）及式（4′）、式（5′）可知，只有當Qf≥Qf0，即Qf≥Q0C時，Q0和Q的函數關系才存在，故Qf的取值范圍為Q0C≤Qf≤Q0。

4 實際散體的移動過渡方程

4.1 密度方程

類橢球體理論經實際觀察和研究，建立了散體放出過程中移動范圍內的密度方程：

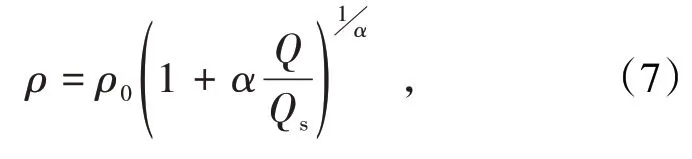
式中，ρ0為放出密度；α為密度變化系數，是與靜止密度（處室密度ρa）和放出密度ρ0有關常數；ρ為移動范圍內任一點的密度。

式（7）經檢驗符合實際，且與速度方程一同通過了移動連續性的理論檢驗，可以認為是類橢球體理論的理論方程［5］。

4.2 移動體平均密度ρCQ計算

根據類橢球體放礦理論的密度方程，計算移動體Q內的平均密度ρCQ。

式（8）、式（8′）即為ρCQ的計算式。

4.3 類橢球體放礦理論實際散體的移動過渡方程

4.3.1 實際散體的質量平衡方程

將式（8′）代入式（1）和式（6），得

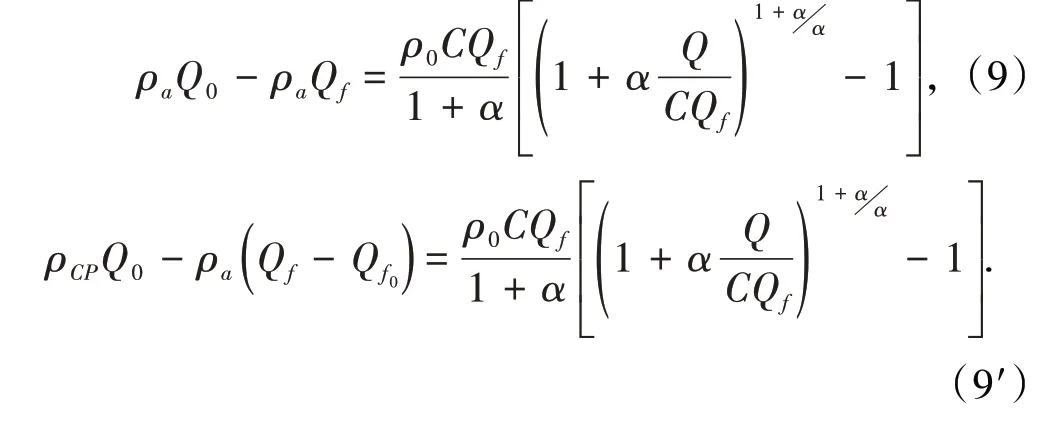
式（9）變換整理得：

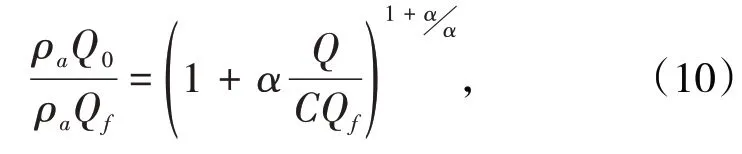
或

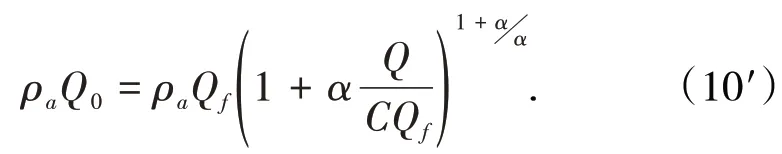
式（10）、式（10′）為實際散體的質量平衡方程。

4.3.2 實際散體的移動過渡方程

對式（10）、式（10′）經變換整理得：

或

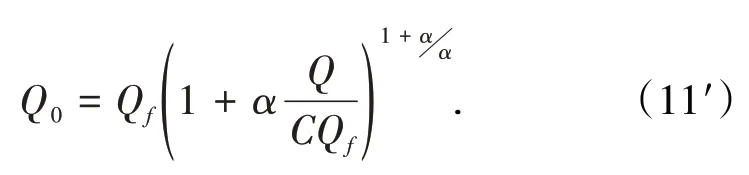
式（11）、式（11′）為實際散體的移動過渡方程。

式（11）、式（11′）經變換整理可表達為

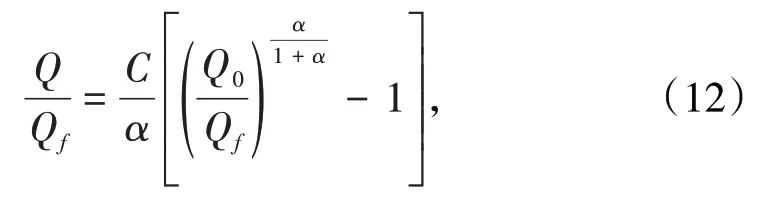
或

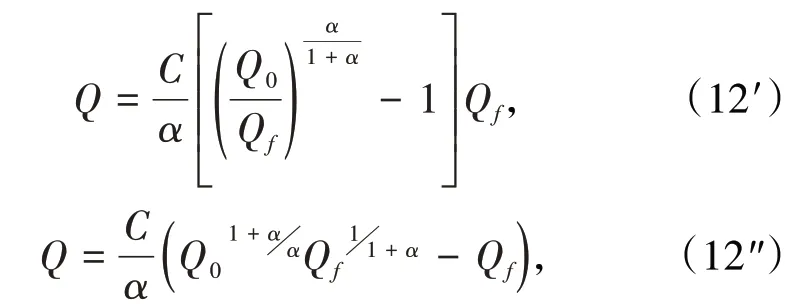
式（12）、式（12′）、式（12"）也為實際散體的移動過渡方程。

4.3.3 實際散體移動過渡方程的討論

（1）當放出體Qf＜Q0C時，Qs＜Q0，此時，Q0表面顆粒靜止不動，由式（4）和式（4′）式知，Q和Q0、Qs不存在函數關系，因此，移動過渡方程式（11）、式（11′）、式（12）、式（12′）不反映Qf＜Q0C時的狀態，移動過渡方程式（11）、式（11′）、式（12）、式（12′）中Qf的取值范圍是Q0C≤Qf≤Q0。

（2）當Qf=Q0，由式（12′）可知Q=0，即Q0表面顆粒全部放出，Q變為零。

（3）當Qf=Q0C時，由式（12′）可知：

Q=CQf=Q0，即Q0表面顆粒即將投入運動，處于臨界狀態。

（4）當η=1時，根據η=可知：α→∞，此時，代入式（12′）得：

式（13）與式（3）完全相同，為類橢球體放礦理論理想散體的移動過渡方程，因此，理想散體的移動過渡方程是實際散體移動過渡方程η=1的特殊方程。

5 結 論

（1）移動過渡原理和質量守恒定律是類橢球體放礦理論移動過渡方程建立的基礎。

（3）實際散體移動過渡方程中，Q0表面顆粒有靜止狀態、極限狀態和移動狀態3種質量平衡關系。

（5）類橢球體放礦理論理想散體的移動過渡方程是Q=Q0-Qf，它是實際散體移動過渡方程當η=1時的特殊方程。