致密油氣儲層綜合可壓裂性解釋方法在鄂爾多斯盆地的應用

尚立濤，張燕明，王業晗，肖元相，喬 巖，孫 遜

（1.中國石油集團工程技術研究院有限公司，北京 102206；2.中國石油長慶油田分公司油氣工藝研究院，陜西西安 710016）

鄂爾多斯盆地蘇里格油氣田東部與國外致密油氣相比，壓力系數低，微裂縫發育較少，儲層兩向應力差為7～8 MPa，巖石脆性較強[1]，需要開展體積壓裂試驗。為確保壓裂設計與施工工藝具有針對性，開展儲層工程甜點研究，進一步認識儲層條件下不同壓裂工藝能否形成復雜裂縫。儲層可壓裂性受多種因素的影響，如地質條件、儲層特性、巖石力學參數、天然裂縫發育程度等。借鑒國內外學者的研究成果[2–6]，根據區塊儲層實際特點，建立了考慮脆性指數、斷裂韌性、應力差異、天然裂縫等影響儲層可壓裂性關鍵參數的綜合可壓裂性指數[7–8]，結合儲層壓裂裂縫監測結果對可壓裂性指數進行了效果評價。

1 可壓裂性的不同影響因素

1.1 脆性指數

脆性巖石受外力破碎過程中不會出現顯著變形，即沒有明顯的塑性變形的特征，反映巖石在破碎前的不可逆變形中并沒有明顯吸收機械能量。致密油氣儲層的脆性較好，壓裂時容易形成復雜裂縫；反之，脆性較差，人工裂縫的導流能力會下降，影響致密油氣的改造效果。脆性指數可通過儲層礦物含量、巖石力學性質、巖心實驗等多種方法進行表征與計算[9–13]，楊氏模量越高，儲層抵抗變形的能力越強，泊松比反映了巖石受力后橫向變形的能力。楊氏模量越高，泊松比越低，脆性越強?；趹兦€的巖石脆性特征定量表征方法能代表壓裂時儲層破碎特征，受實際儲層巖心的限制，無法實現全井段脆性實驗。因此，應用聲波測井資料計算得到儲層巖石力學參數，結合室內靜態實驗數據對測井解釋動態數據進行修正，將動態參數轉換為靜態參數。采用楊氏模量法和泊松比法（圖1和圖2）確定研究區儲層巖石脆性指數，根據研究區巖心巖石力學實驗數據，得到適用于工程應用的巖石靜態參數計算致密油氣儲層脆性指數的方法，然后通過巖心脆性實驗結果校正（圖3），建立研究區基于儲層力學參數計算的脆性指數計算方法。

圖1 巖心楊氏模量實驗數據

圖2 巖心泊松比實驗數據

圖3 巖心脆性實驗數據與力學參數計算脆性

根據研究區巖心巖石力學參數實驗（最大楊氏模量為57.6 GPa，最小楊氏模量為13.2 GPa；最大泊松比為0.36，最小泊松比為0.14），建立了基于楊氏模量與泊松比的校正脆性計算方法：

式中：Ym為基于儲層楊氏模量的脆性計算結果，無因次；Pr為基于儲層泊松比的脆性計算結果，無因次；E為靜態楊氏模量，GPa；R為泊松比；FI1為基于脆性指數的可壓性指數。

應用楊氏模量與泊松比計算并經過巖心實驗脆性結果校正巖石脆性指數。

1.2 斷裂韌性指數

斷裂韌性同樣是影響儲層壓裂難易程度的主要因素，反映壓裂過程中裂縫形成后維持裂縫向前延伸的能力。斷裂韌性實驗繁瑣、隨機性大，斷裂韌性的計算主要基于斷裂韌性與抗拉強度擬合公式[8]。儲層巖石的破壞行為本質上是能量耗散和釋放的宏觀體現，峰后斷裂能反映裂紋擴展所消耗的能量，是決定巖石是否發生斷裂的本質因素。巖石斷裂能越大，壓裂裂縫寬度越小，裂縫長度越大。楊氏模量對巖石斷裂能的大小和裂縫的形成有直接的影響，基于巖心實驗建立不同圍壓下峰后斷裂能密度與楊氏模量的擬合公式，利用峰后斷裂能密度可定量表征研究區致密砂巖斷裂韌性：

考慮斷裂韌性的可壓裂性指數FI2公式如下：

式中：Gz為巖石斷裂能密度，N·mm/mm3；FI2為考慮斷裂韌性的可壓性指數。

1.3 地應力指數

儲層應力差的大小直接影響壓裂人工裂縫形態。為建立準確應力差指數評價裂縫復雜程度方法，首先對區塊地應力解釋方法進行校正，同樣根據測井數據計算地應力，應用巖心實驗結果進行校正。

研究區儲層巖石力學參數測試表明，平均應力梯度為0.016～0.018 MPa/m（圖4），平均水平應力差7.0 MPa（圖5），儲層和隔層應力差為5.2 MPa。基于巖石力學參數測試與實際施工數據校正測井數據解釋結果，準確解釋改造井段力學參數、應力差，應用測井數據解釋最小主應力與壓裂施工測試數據一致，實現對全井段的水平應力差的計算。歸一化水平應力差指數可表示為：

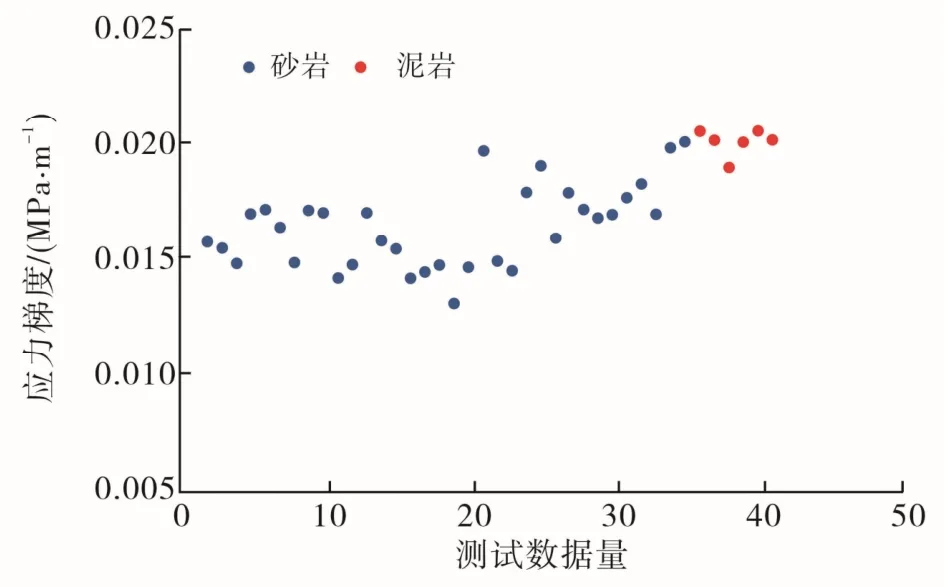
圖4 砂泥巖儲層巖心地應力實驗數據統計

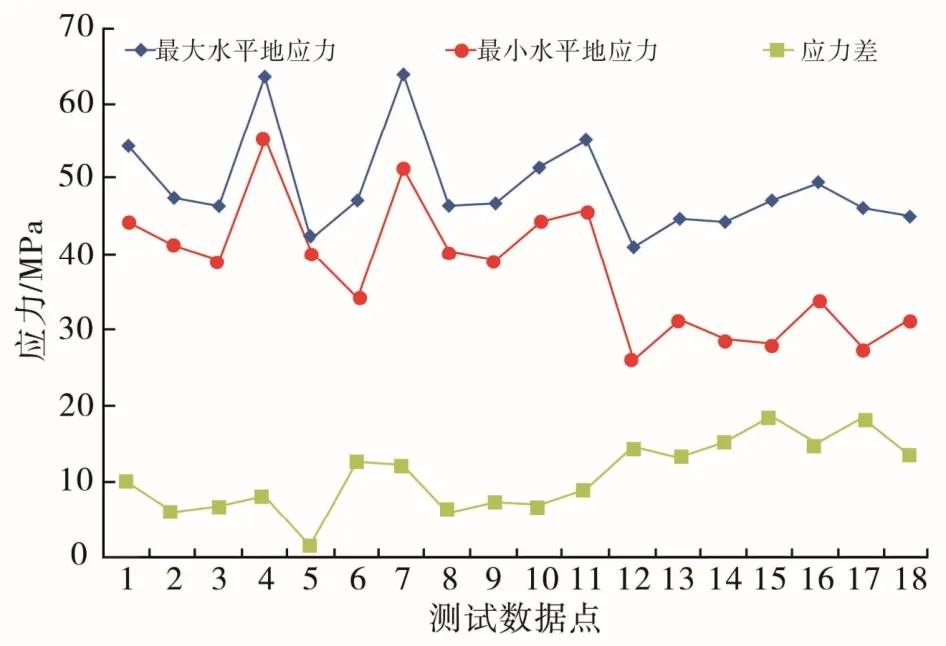
圖5 致密砂巖儲層應力差實驗數據統計

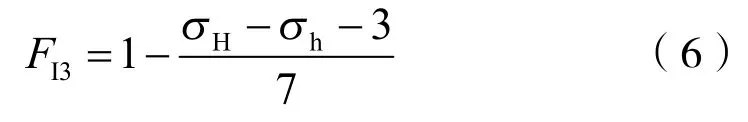
式中：FI3為歸一化的水平應力差指數；σH為最大水平應力差，MPa；σh為最小水平應力差，MPa。

1.4 天然裂縫指數

天然裂縫的廣泛發育可以降低儲層自身的抗張強度，使儲層受壓起裂更簡單。在壓裂過程中，天然裂縫和誘導裂縫相互影響，人工裂縫可以使天然裂縫重新張開并相互溝通，天然裂縫也可以改變誘導裂縫的延伸方向，產生下一級誘導裂縫，并最終形成復雜裂縫體系。天然裂縫長度越長，可壓裂性越好；天然裂縫密度越大，可壓裂性越好。根據數值模擬研究結果，天然裂縫與水平最大主應力方向夾角越小，裂縫越容易開啟但轉向角度小；夾角越大，裂縫轉向角度越大但難以開啟；當天然裂縫走向與水平最大主應力夾角為30°～60°時最適合產生復雜裂縫體系，天然裂縫易開啟且轉向角度大。由于很多施工井壓裂前未進行成像測井，常規測井資料是進行井中裂縫識別的唯一手段，具有重要的研究及應用價值。前人的研究表明，常規測井孔隙度曲線、電阻率曲線、雙側向電阻率曲線、井徑曲線、聲波曲線等均對天然裂縫具有一定響應[9–10]。提取各常規測井曲線裂縫指示信息，建立裂縫發育概率模型，計算裂縫發育概率曲線，進行裂縫發育定量預測。根據裂縫對深淺電阻率、聲波的響應特征差異，構造深淺電阻率、聲波差異比值特征參數，建立基于測井解釋的天然裂縫指數評價：

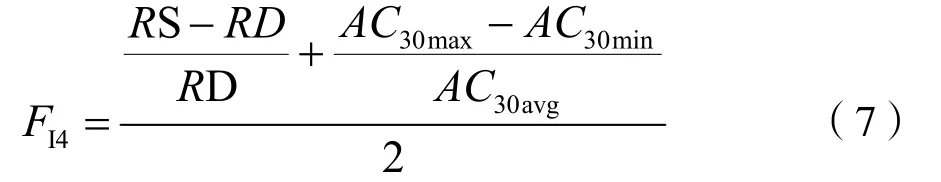
式中：FI4為考慮天然裂縫發育程度的可壓裂性指數；RS為淺電阻率，Ω·m；RD為深電阻率，Ω·m；AC30max、AC30min、AC30avg分別為每30個數據組的最大、最小和平均聲波時差，μs/ft。

基于室內巖石力學測試和測井曲線解釋結果，考慮脆性、斷裂韌性、水平地應力差和天然裂縫發育程度等因素作為可壓裂性評價指標，歸一化處理各參數后，建立適用于致密性儲層的可壓裂性評價模型。

2 綜合可壓裂性解釋模型與圖版

2.1 計算權重

工程實踐表明，天然裂縫發育程度能反映儲層的可壓裂性，水平應力差、脆性指數和斷裂韌性系數對儲層的可壓裂性影響很大。判斷矩陣表示某一層元素之間相對于上一層元素的重要程度，利用表1中1～9的比例標度來表示這種程度，用可壓裂性相關的各參數對比后的標度值構造判斷矩陣[4]（表2）。

表1 判斷矩陣標度

表2 判斷矩陣

計算判斷矩陣的最大特征及其對應的特征向量，同時模擬不同因素對壓裂改造體積的影響程度，從而確定可壓裂性各影響因素的權重，可得天然裂縫發育、水平應力差、脆性指數、斷裂韌性所對應的權重值分別為0.51，0.24，0.15，0.10。

2.2 綜合可壓裂性評價模型

考慮脆性指數、斷裂韌性、水平應力差、天然裂縫發育得到綜合可壓裂性指數：

式中：FIf為綜合可壓裂性指數，無量綱；FI1為考慮脆性指數的可壓裂性指數，權重系數為0.15；FI2為考慮斷裂韌性的可壓裂性指數，權重系數為0.10；FI3為考慮水平地應力差的可壓裂性指數，權重系數為0.24；FI4為考慮裂縫發育程度的可壓裂性指數，權重系數為0.51。

根據區塊蘇東56–X1井測井解釋數據，計算了儲層脆性指數、斷裂韌性指數、應力差指數、天然裂縫指數等影響儲層可壓裂性關鍵參數，并計算形成綜合可壓裂性指數，解釋結果用于與地質甜點結合確定最優改造層段（圖6）。

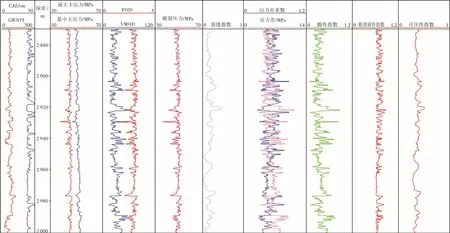
圖6 蘇東56–X1井綜合可壓裂性解釋剖面

根據綜合可壓裂性指數解釋結果，應用數值模擬水平井一段壓裂3簇，簇間距20 m，施工排量15.0 m3/min。壓后裂縫波及寬度與裂縫長度比值定義為FCI，模擬結果表明，裂縫綜合可壓裂性指數越大，壓后裂縫復雜程度越高（圖7）。

圖7 可壓裂性指數與裂縫復雜程度關系

結合國內外致密油氣藏壓裂開發經驗，脆性指數、斷裂韌性與水平地應力差以及天然裂縫發育情況得到的可壓裂性系數不一致時，儲層的可壓裂性評價結果不同。可壓裂性指數越大，通過壓裂施工產生的裂縫形態越復雜，儲層的可壓裂性級別越高；可壓裂性指數越小，壓裂施工產生的裂縫形態越簡單，儲層的可壓裂性級別越低。定義可壓裂性指數大于0.60的儲層為一級儲層，可壓裂性好；可壓裂性指數為0.30～0.60的為二級儲層，可壓裂性一般，需要通過增大施工凈壓力或者其他輔助措施提高改造效果；可壓裂性指數小于0.30的儲層為三級儲層，可壓裂性差。

2.3 裂縫監測結果評價

計算井下微地震裂縫監測的3口井的多段儲層可壓裂性指數，解釋結果為0.28～0.49，解釋儲層為可壓裂性一般，對應裂縫復雜程度監測結果為0.09～0.48，整體裂縫復雜程度低，可壓裂性解釋結果與實際裂縫監測結果較為一致（圖8）。研究區致密油氣儲層綜合可壓裂性指數能用于判斷形成裂縫的復雜程度。研究區解釋可壓裂性指數一般為0.3～0.5，判斷壓裂無法形成大規模復雜裂縫體系，為提高壓裂改造體積，需要優化施工工藝與工程參數。

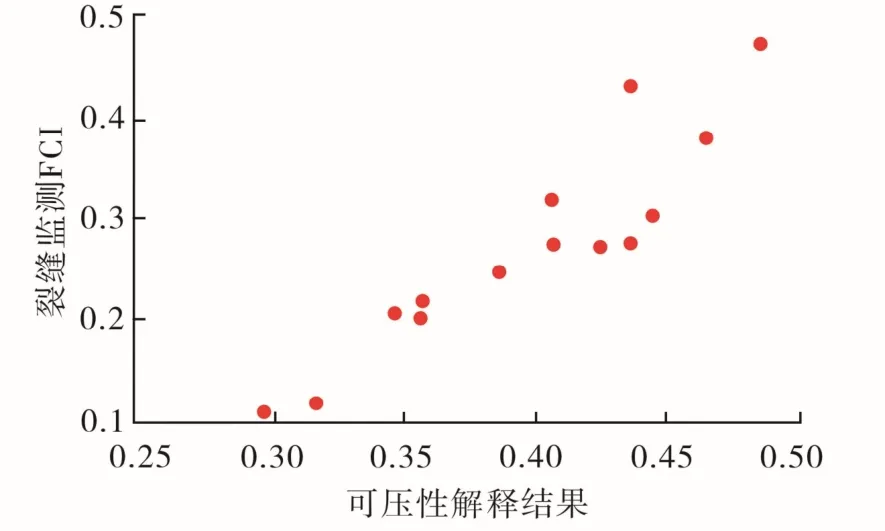
圖8 裂縫監測監測結果復雜性分析

3 結論

（1）結合室內靜態實驗數據對測井解釋動態數據進行修正，得到適用于工程應用的巖石靜態參數計算致密油氣儲層脆性指數、地應力指數方法。

（2）基于儲層巖石力學參數、脆性指數、斷裂韌性和天然裂縫發育程度等適用于致密油氣儲層的可壓裂性評價模型，應用參數歸一化方法分析各參數影響權重，建立了綜合可壓裂性指數解釋模型。

（3）解釋的綜合可壓裂性指數與裂縫監測復雜程度結果較為一致，可作為人工裂縫形態的判斷依據，能夠有效指導壓裂方案優化，提高壓裂設計的針對性。