格構式錨桿擋墻體系中格構梁跨度影響因素

俞美華 寧萬輝

(1.湖北地環巖土工程有限公司，湖北 荊州 434000； 2.武漢鐵路局荊門橋工段，湖北 宜昌 443000)

1 概述

格構式錨桿擋墻由錨桿和縱橫梁組成邊坡永久性支護結構，不僅能夠嚴格控制邊坡坡體的變形，還能在格構梁內噴播植草，美化環境，在鐵路、公路、水利、市政等各行業應用廣泛。近年來格構梁的跨度，即縱梁的跨度根據規范及經驗取值，跨度一般為3 m～5 m，2 m或6 m的跨度一般較少采用?？缍热≈挡缓侠?，不僅會增加工程造價，還會釀出工程質量事故。本文從三個方面，即格構梁設計、群錨效應及巖土體擠壓效應綜合確定跨度的最優值。

2 格構梁設計的影響

格構梁內力(彎矩的作用較大)一般要求結構相同處越均勻越好，因此設計時以此為準則。格構梁的跨度對其內力分布有重要影響，內力計算決定著它的配筋，配筋滿足與否又決定著整個體系對邊坡的加固情況，因此，分析格構梁的跨度有其必要性。為了研究格構梁跨度對其內力的影響，以平面體系為研究對象，需建立如下參數模型，如表1所示。

表1 研究格構梁跨度對內力影響時彈性地基梁計算模型參數

建立以上模型，采用理正軟件進行計算與分析。

格構梁自由段的長度，按照已有的研究成果，取0.3L。這樣得出的模型平面圖見圖1。

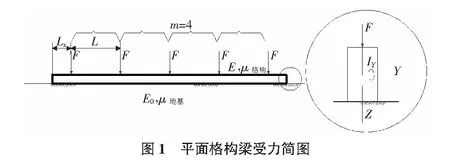
如圖1所示，錨桿作用力簡化成節點處的集中力。為了便于描述格構梁內力，將模型平面圖的各部位稱謂進行統一，如圖2所示。

計算時采用彈性半無限空間地基模型，不考慮梁的自重，荷載與活載的分項系數均設為1。計算結果見表2及圖3。

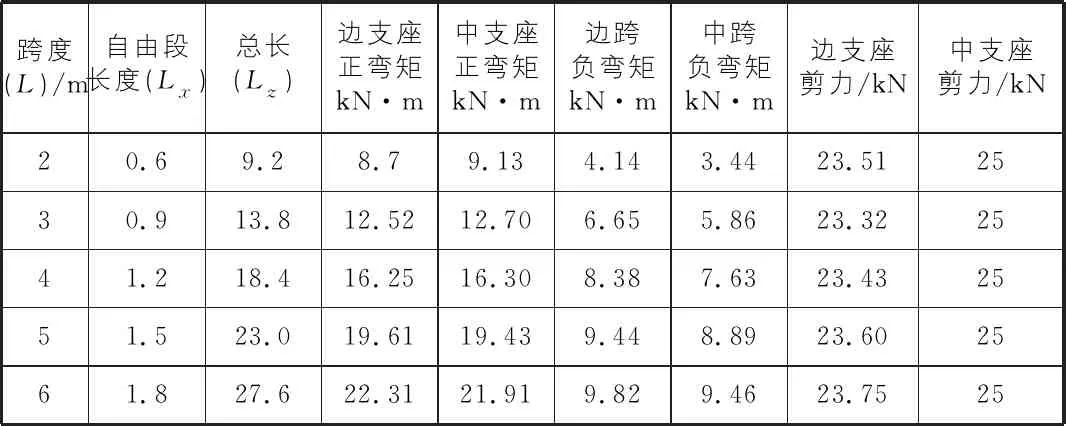
表2 各跨度時格構梁的內力

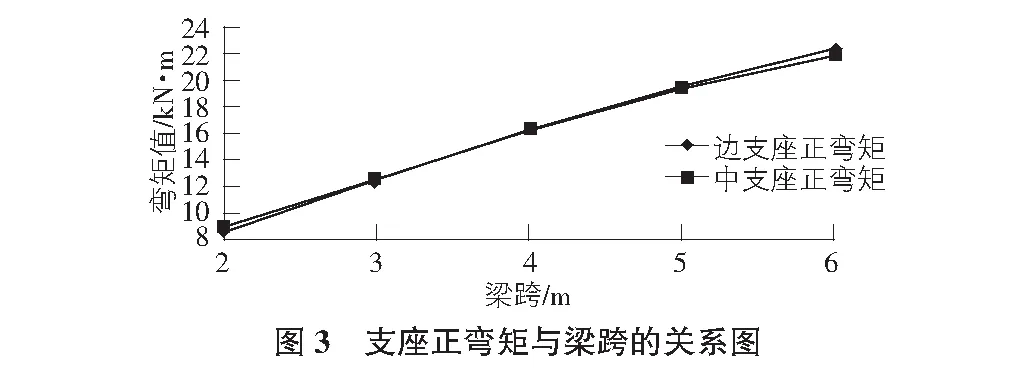
由表2可知，邊支座的正彎矩要大于跨中的負彎矩絕對值，配筋時應按照最大彎矩來合理配筋。格構的彎矩值隨著跨度的增大而增大，剪力值不敏感。而且隨著跨度從2 m增大到4 m，邊支座的彎矩和中支座的彎矩值逐漸接近；從4 m再增大到6 m，邊支座的彎矩和中支座的彎矩值逐漸拉開。2 m跨度時梁支座的彎矩幅度相差5%，4 m跨度時彎矩幅度相差0.3%，6 m跨度時彎矩幅度相差1.8%。因此，從圖1～圖3可看出當格構跨度為4 m時，支座彎矩分配最均勻，同時自由段的長度可取1.2 m。

3 群錨效應的影響

錨桿的間距即格構梁的跨度，作為錨桿設計的重要環節之一，對格構式錨桿擋墻設計影響重大。如果錨桿間距過大較為稀疏，則單根錨桿的錨固力過大，由此造成應力集中現象；如果錨桿間距過小較為密集，又會發生群錨效應而降低單根錨索錨固的作用。

群錨效應就是因為巖土體內部的應力場疊加而形成的，工程實踐中為了減小群錨效應，一般以剪應力的影響范圍來確定錨桿的間距[1]。

結合多年理論與實踐研究，各國對錨桿的最小間距都做出了部分規定：日本規定最小間距在1.5 m以上；美國規定最小間距取內錨固段直徑的6倍以上；我國規范也規定錨桿的最小間距不得小于1.5 m。

同時在日本建筑標準結構設計標準(1974)的規范中明確規定，群錨ls最小間距應滿足(見式(1))：

(1)

式中：r——錨固段的平均半徑，m；

l——錨固段長度,m；

ls——錨桿最小間距。

對于錨桿最大間距，也應做出限制，結合我國多個工程分析研究，錨桿的最大間距，文獻[1]建議一般間距不宜大于4 m。

由以上內容可知，錨桿間距一般要大于最小錨桿間距ls，不宜大于4 m。

4 巖土體擠壓效應的影響

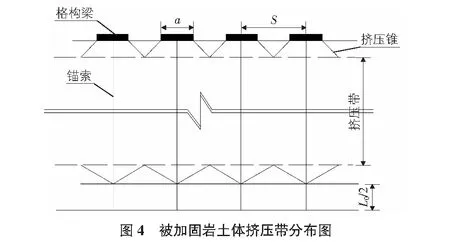
錨桿在被加固邊坡巖土體中會形成一定厚度的擠壓帶。從邊坡穩定性的角度出發，它既要求潛在滑面落在擠壓帶以內，又要求具有較厚的擠壓帶。根據錨固力在巖土中的擴散傳遞可知，擠壓帶的厚度主要取決于錨桿長度及其間距，其厚度一般應為2/3錨桿長考慮[2]。有試驗結果表明，巖土體受擠壓作用沿格構梁底部和錨固段中部呈倒錐形破壞，角度為60°～90°[3]。假定格構梁寬度a范圍內壓力均勻分布(如圖4所示)，則格構梁間距S可由式(2)求出，錨桿總長度等于擠壓帶厚度、兩端擠壓錐厚度及錨固段1/2長度之和。錨固段長度為L0，L0一般為(0.3～0.5)L[4]，且L0≤10 m。

(2)

式中：L——錨桿總長度，m；

a——格構梁壓力均勻分布寬度，m；

S——格構梁間距。

應力愈大的錨桿，由于局部巖土體受力大，錨索長，故取較小值，反之則取較大值。工程應用中若能準確的判斷擠壓錐的擴散角度以及擠壓帶的厚度，則按上述理論分析可得到較合理的格構梁跨度。在缺乏確切數據的情況下及正確指導方法的時候，建議格構梁跨度在(2.5～5.0)m范圍內取值。

5 結語

綜合以上格構梁自身設計的影響、群錨效應的影響及巖土體擠壓效應的影響三方面對格構梁跨度進行研究時得出：在不具備實驗條件及無法獲得正確數據的前提下，根據國內外經驗參數，格構梁的跨度建議在3 m～5 m范圍內尋求最優值。