不同波形的波紋鋼拱橋力學性能分析與測試

藺 廣 花

(延長油田股份有限公司吳起采油廠，陜西 延安 717600)

1 概述

目前，我國道路橋梁方面的建設多采用圬工砌體及鋼筋混凝土組合結構等傳統材料，也采用鋼波紋板結構等新型材料進行橋梁建設[1,2]。傳統材料進行橋梁建設存在很多缺點，如工期長、地基承載力高、沉降不均勻等[3,4]。

鋼波紋板拱橋是一種采用波紋狀弧形板，通過連接、拼裝形成拱橋的新型鋼結構形式。鋼波紋板相較于傳統材料具有自重輕、方便運輸、施工簡單、變形適應好和抗拉、剪和疲勞性能等優勢[5]。曹海洋和唐陽使用有限元法對比了波紋鋼管涵與圓形鋼管涵的受力性能，發現波紋鋼管涵的結構變形小于圓形鋼管涵的結構變形[6]。陳玉留等采用有限元分析法，發現波紋鋼在正常荷載和泥石流荷載條件下均能夠滿足明洞支護結構變形與受力的要求[7]。Yeau等基于鋼波紋管涵洞在靜態和動態的汽車荷載作用下撓度和應變變化的研究，發現涵洞的撓度隨著填土高度的增加非線性減小，動態汽車負荷下，涵洞的最大撓度比靜態汽車負荷下的最大撓度減少10%～30%，且與汽車的總荷載無關[8]。Manko等對鋼波紋板橋涵進行靜力測試，測試結果表明有限元計算出的應力和平均位移結果比實測結果高，且與結構的永久變形無關[9]。D.Beben研究了鋼波紋板涵洞的位移和應變，發現在涵洞管頂1/4位置處位移最大，在管側1/4位置處應變最大[10]。M.Ju和H.Oh基于波紋鋼板螺栓連接的靜力和疲勞性能研究結果，發現波紋鋼板涵洞橋與傳統橋梁相比是最適合橋梁快速重建的紐帶[11]。

隨著國內越來越多的地區修建波紋鋼拱橋來代替傳統橋梁結構，如何選取合適的波紋鋼拱橋參數是急需解決的難題。本文采用柔性薄殼波紋鋼結構建設新型橋梁，使用有限元法分析不同波形中小跨徑波紋鋼拱橋的力學性能，并與現場實測數據進行對比，為以后的研究及應用提供參考。

2 材料與方法

2.1 有限元仿真建模

結合工程實際及文獻調研，仿真過程中鋼波紋板簡化為殼體，選用Shell63單元，拱外部分簡化為實體單元，選用Solid45單元。波紋鋼拱橋結構材料的屬性參數如表1所示。

表1 材料屬性參數

以不同波形的波紋鋼為研究對象，采用有限元軟件建立不同的仿真模型，各仿真模型的結構參數如表2所示，并對中小跨徑波紋鋼拱橋波峰和波谷處的撓度和應力的變化規律進行對比分析。選擇各仿真模型周向0°，15°，30°，45°，60°，75°和90°斷面處的數據進行對比分析。

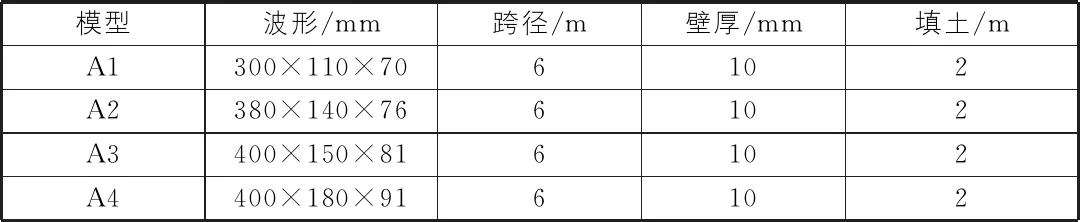
表2 不同波形模型結構參數

2.2 現場測試方案

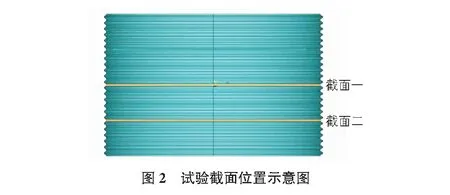
根據現場試驗條件，波紋鋼管內上凸處為波峰，下凹處為波谷。測點布設位置均按照0°，15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°和180°的15°間隔均勻布置。定義0°與180°截面為拱橋的拱腳，90°截面為拱橋的拱頂，如圖1所示。

本文現場試驗包括應變和撓度測試，且兩項測試同時進行。具體工況如圖2所示。截面1為道路中心線位置，距離道路中心線2 m處為截面2，在截面1和2波峰及波谷的徑向位置粘結應變片。

使用靜態應變采集儀對施工現場的中小跨徑波紋鋼拱橋在車輛荷載作用下的應變值進行測量。采用千分表測量波紋鋼拱橋的撓度值，以90°撓度為主。撓度測試與應變測試同時進行。圖3a)為粘貼應變片的過程，圖3b)為采集數據的過程，施工現場建造的波紋鋼拱橋如圖3c)所示。

3 結果與分析

3.1 波峰有限元模擬分析

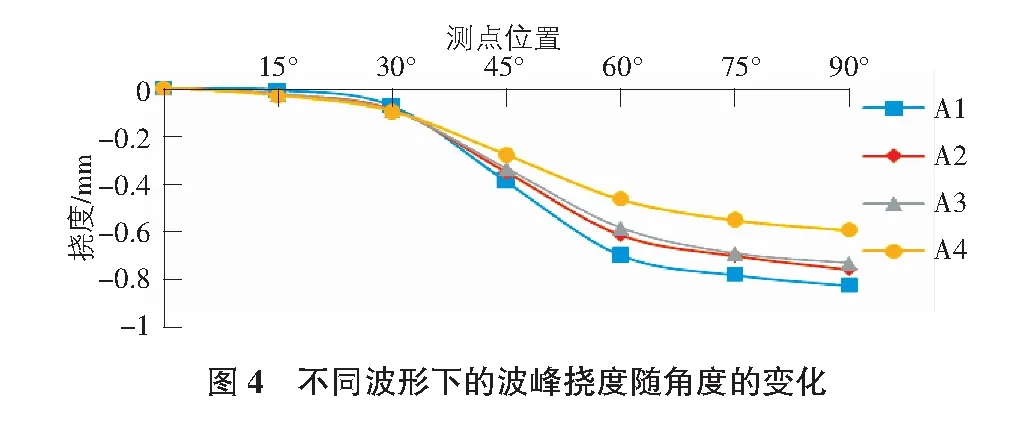
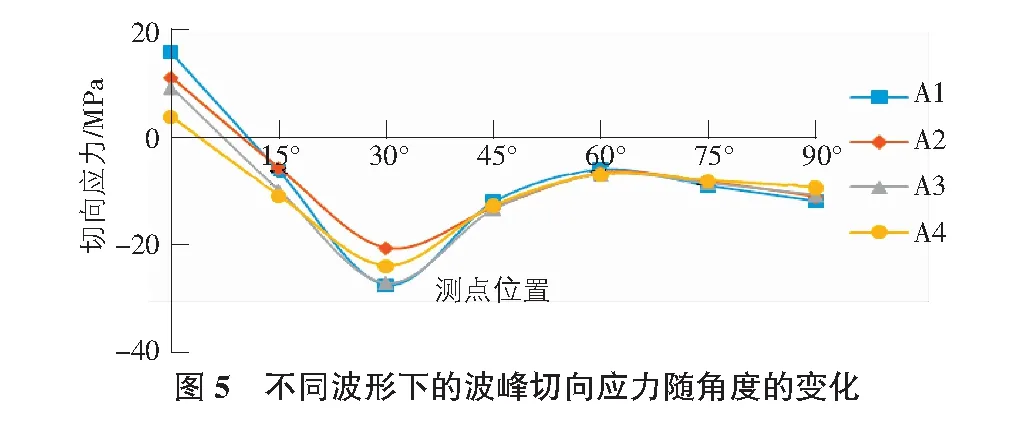
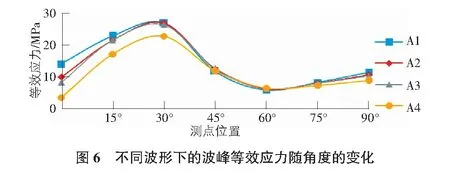
由圖4～圖6可以看出，四種不同波形波紋鋼拱橋撓度的絕對值整體沿著0°～90°的位置逐漸增大，方向均向下。在0°～30°截面處，四個拱橋模型的撓度絕對值基本相同；對于其他角度截面上的撓度絕對值，模型A1>A2>A3>A4，表明隨著拱橋的波距和波高增大，撓度絕對值減小。四個模型在0°截面處均表現為拉應力，且從拱腳至拱頂的方向拉應力逐漸減小，然后均表現為壓應力，隨著波距減小，拉應力絕對值增大，但切向應力絕對值近似相等，模型A4的切向應力絕對值略小于其他三種模型的切向應力絕對值。壓應力絕對值的變化規律為先增大后減小，在60°處又逐漸增大直至拱頂處。四種模型的等效應力均表現為拉應力，等效應力值均先增大后減小，之后略有增大。在45°，60°及75°截面處，四個模型的等效應力值基本相同。其余截面處，模型A1>A2>A3>A4的等效應力值。

3.2 有限元模擬分析波谷變化規律

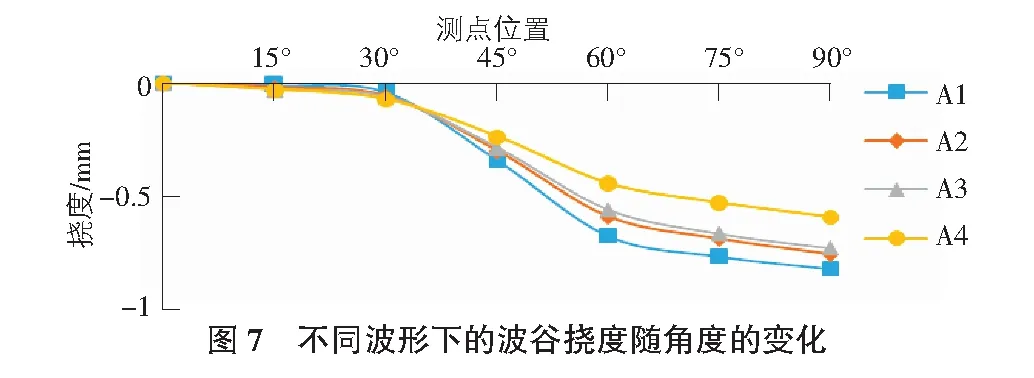
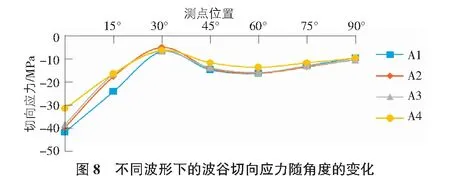
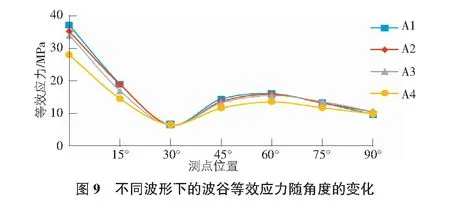
由圖7～圖9可以看出，四種不同波形波紋鋼拱橋的撓度絕對值從0°到90°位置逐漸增大，在90°位置均達到最大，且撓度方向均向下。隨著波距的增大，撓度絕對值逐漸減小。四種模型的切向應力均表現為壓應力，均先減小后增大。模型A1>模型A2>模型A3>模型A4的切向應力絕對值。四種模型的等效應力均表現為拉應力，且應力值在30°與90°截面處基本相等，在其余截面處，波距越小，等效應力值越大。

3.3 有限元模擬對比分析波峰和波谷變化規律

由圖1～圖6可知，模型A1波峰和波谷處撓度變化規律基本相同，撓度方向均向下，且撓度絕對值從0°到90°逐漸增大；波峰、波谷處切向應力的變化規律存在明顯差異，模型A1在0°截面處的應力為拉應力，其他三個模型均為壓應力；波峰、波谷處等效應力的變化規律完全相反，且均為拉應力。在截面的0°及30°處，波峰與波谷的等效應力的差值和切向應力絕對值的差值均為最大值，可知在這兩處存在明顯彎矩。

模型A2波峰和波谷的撓度方向均向下，且撓度變化基本一致；拱腳處波峰的切向應力為拉應力，波谷的切向應力為壓應力，拱腳處波谷的切向應力絕對值大于波峰的切向應力值，且在拱腳處的彎矩最大。拱頂處波峰和波谷的切向應力絕對值的差值與等效應力值的差值均最小。模型A2波峰切向應力絕對值在拱腳處為拉應力，再逐漸減小到0，然后逐漸增大，在30°又減小。波谷的切向應力絕對值先減小然后增大。

模型A3波峰和波谷處撓度絕對值沿著拱腳到拱頂的方向呈現逐漸增大的趨勢，且波谷處的撓度略大于波峰處的撓度，方向均向下。波谷處切向應力及等效應力均先減小然后增大之后略有降低，而波峰處的變化規律與之相反，且縱向看來，波峰和波谷切向應力與等效應力值均存在明顯的數值差，在15°與90°處差值較小。波谷切向應力與等效應力最大值均在0°處，最小值均在30°處。

模型A4撓度、切向應力和等效應力的變化規律與其他三個模型的變化規律相同，即撓度從拱腳到拱頂方向增大，且波谷的撓度值略大，方向均向下；波谷處切向應力和等效應力值均先減小，再增大，然后略有降低；波峰的切向應力在拱腳處為拉應力，在其他角度處與波谷的變化規律相反。

3.4 現場實測值與有限元模擬值對比分析

由圖10可看出，波紋鋼拱橋截面1波峰和波谷處的應力都發生明顯的變化。截面1在0°與180°處，波峰均為拉應力，從0°～180°應力變化規律為：拉應力→壓應力→拉應力的變化過程。拉應力最大值為18 MPa。在截面1的180°處，波谷的應力絕對值最大，應力為57 MPa；在30°處波谷應力最小，應力值為7 MPa，且截面1波谷均為壓應力。

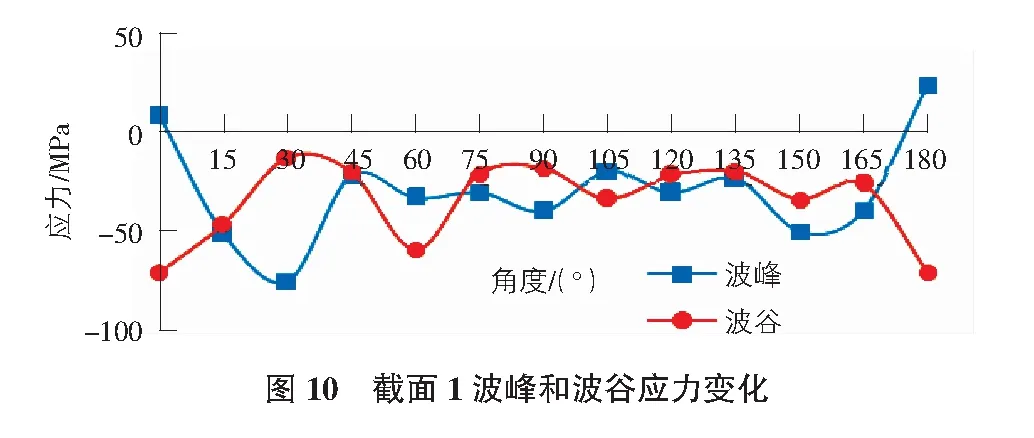
由圖11可知，波紋鋼拱橋截面2波峰和波谷均表現為壓應力，應力值的變化規律基本相反。波峰應力絕對值最大值在180°截面處，應力值為-59 MPa。截面2波谷壓應力絕對值最大值在165°截面處，應力值為-73 MPa，壓應力絕對值最小處為0°處，為-27 MPa。

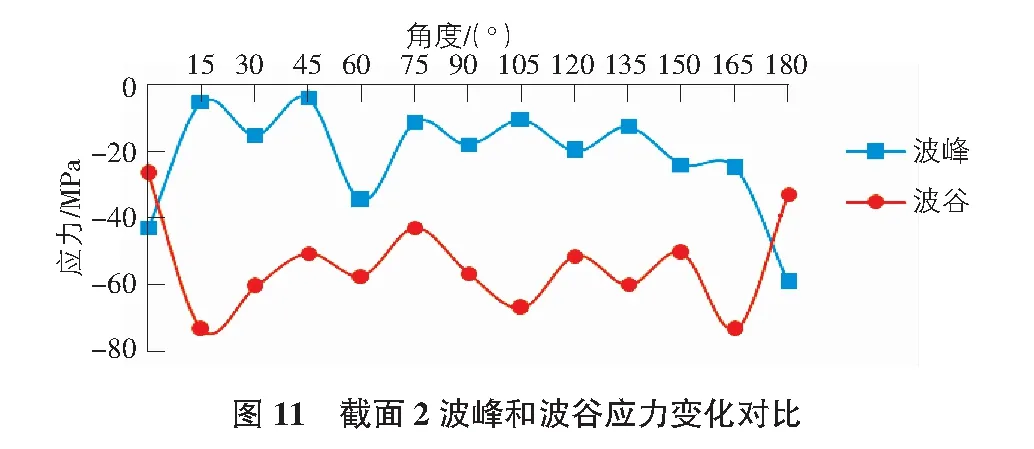
由圖12可以看出，汽車荷載作用在拱橋上時，截面1波峰和波谷處撓度變化趨勢基本相同。撓度絕對值變化都是從0°到90°整體增大，且最大值均出現在90°處。波峰撓度絕對值最大值為-1.8 mm，波谷撓度絕對值最大值為-1.9 mm。

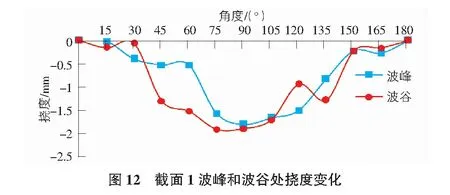
當汽車荷載作用在波紋鋼拱橋橋面上時，截面2波峰和波谷撓度絕對值沿0°向90°截面方向逐漸增大。截面2波峰處撓度絕對值最大值為2 mm，波谷處撓度絕對值最大值為2.3 mm(見圖13)。

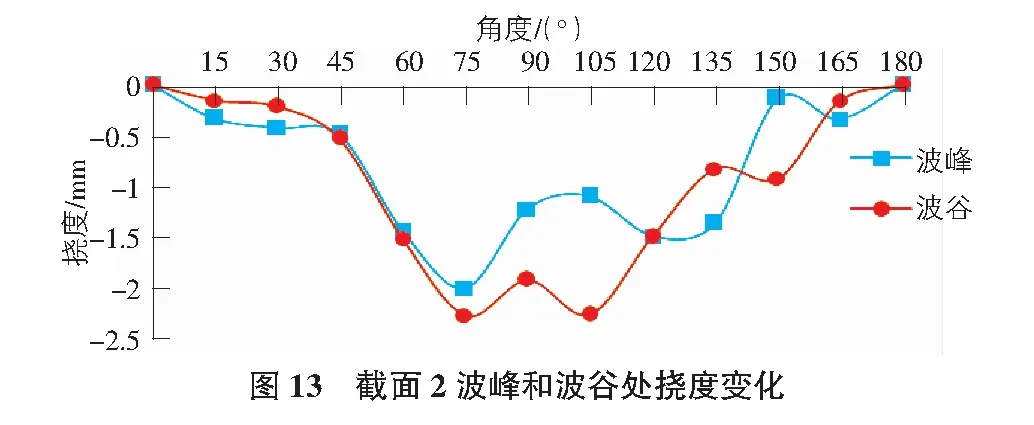
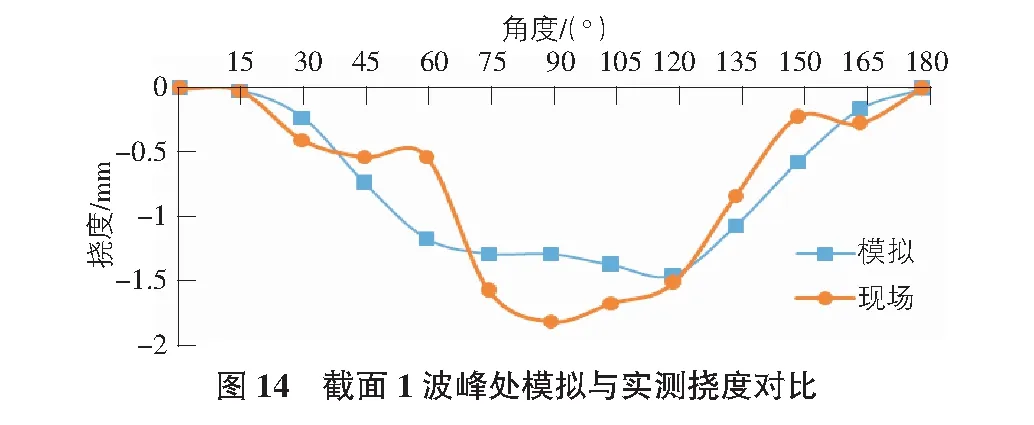
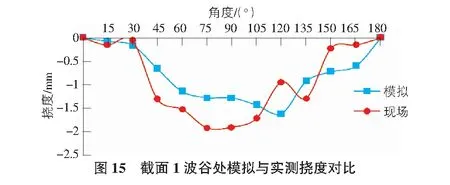
由圖14與圖15可知，截面1波峰處撓度變化規律的模擬與實測結果基本相同，波谷處撓度模擬值與實測值變化趨勢基本相同，現場實測結果明顯大于有限元模擬結果，有限元模擬最大值為1.5 mm，現場實測最大值為2 mm。由截面1波峰和波谷撓度對比可以得出，現場值與模擬值之間存在誤差，但誤差較小。

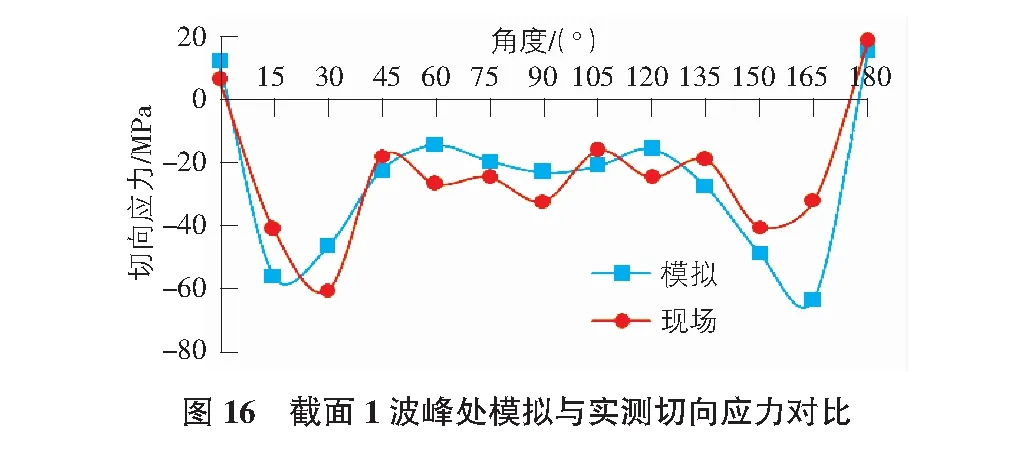
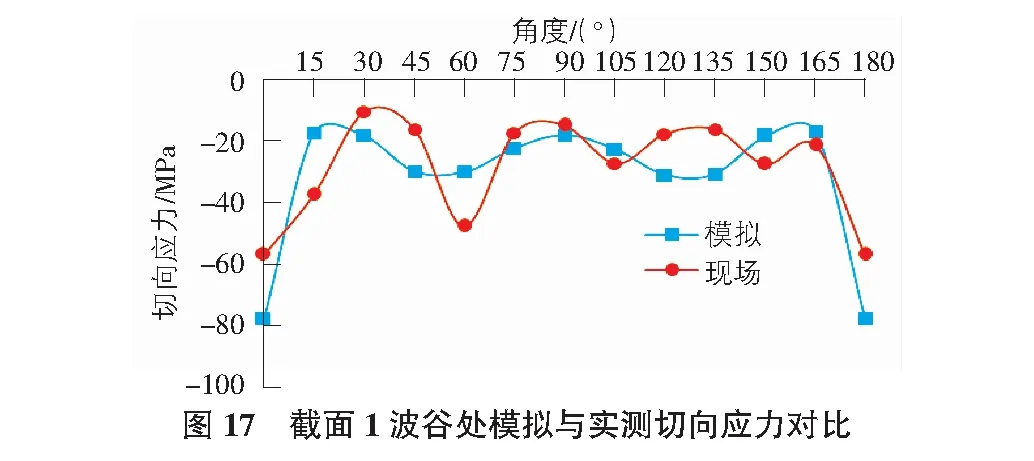
由圖16與圖17可知，截面1波峰切向應力在0°處為拉應力，在其他角度位置均為壓應力。截面1波谷切向應力均為壓應力，在180°處應力值最大。模擬結果與實測結果雖存在明顯誤差，但誤差在可接受范圍內，故有限元模擬結果可用于模擬現場工況。

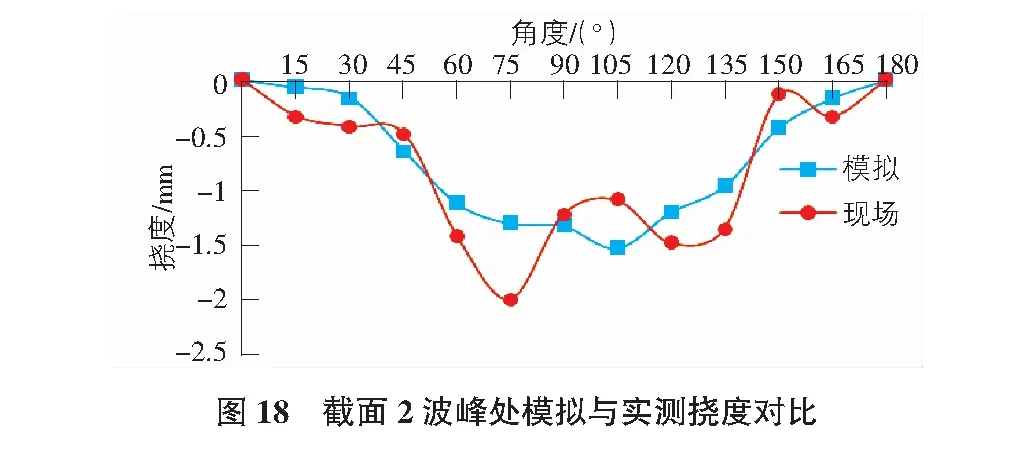
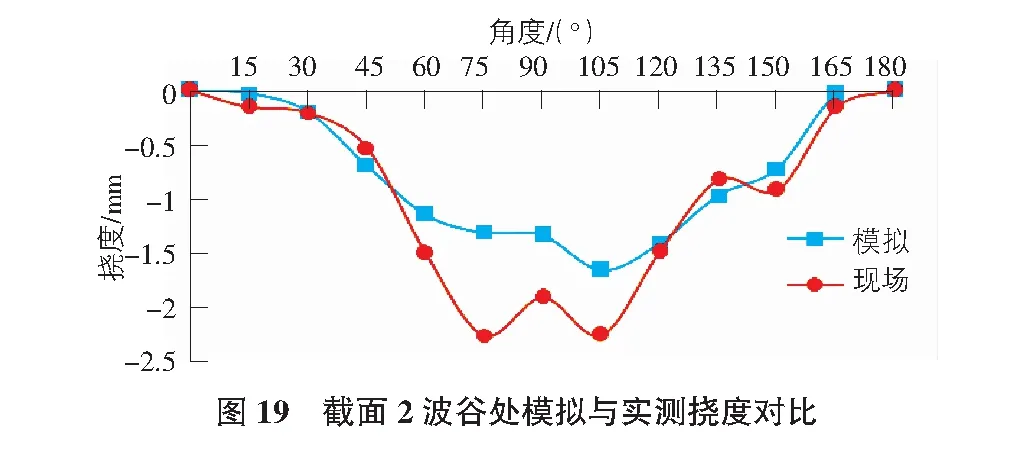
由圖18及圖19可知，截面2波峰和波谷撓度方向均向下，現場實測結果與模擬結果之間存在誤差，且都是從0°到90°逐漸增大。波峰模擬最大值為1.5 mm，現場實測最大值為2 mm；波谷模擬最大值為1.7 mm，現場實測最大值為2.3 mm。綜上，波紋鋼拱橋在車輛荷載作用下，波峰和波谷模擬結果與實測結果存在誤差，誤差最大值為1 mm。

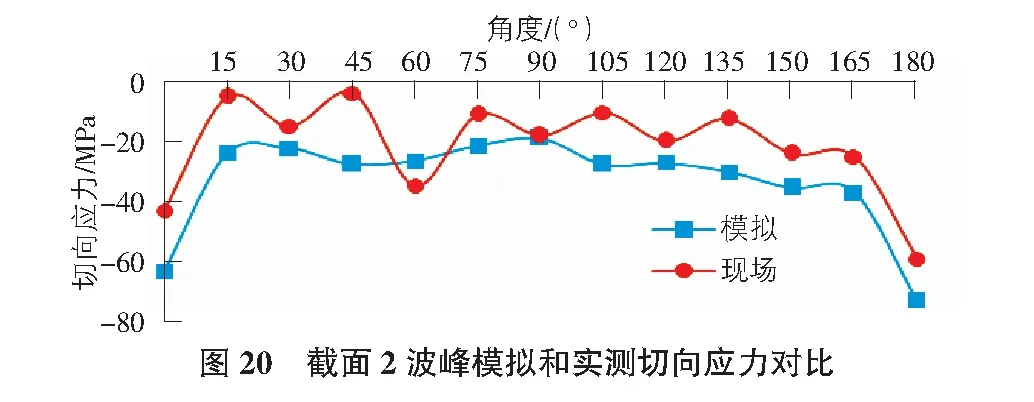
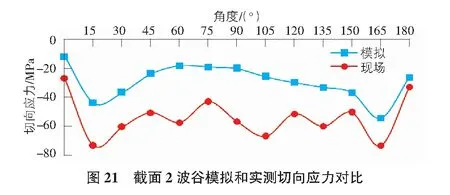
由圖20與圖21可知，截面2波峰和波谷切向應力變化規律完全相反，且均為壓應力。波峰切向應力模擬值大于實測值，而波谷處切向應力模擬值小于實測值。波峰和波谷的切向應力實測值與模擬值有一定的誤差，但變化規律相同，且有明顯的應力應變集中的現象。

由圖14～圖21可以看出，通過對比分析汽車荷載作用于中小跨徑波紋鋼拱橋截面1和截面2波峰與波谷處13個測點的撓度與切向應力的模擬值與實測值可以得出，撓度值的實測值與有限元模擬值基本相同，切向應力的模擬值與現場實測值之間存在誤差，但變化規律相同，且誤差值較小且在合理范圍內。因此所建有限元模型與實際工程情況基本符合，同時也證明了針對中小跨徑波紋鋼拱橋的力學性能問題，使用有限元數值模擬分析法是可行的。

現場實測結果與有限元模擬結果之間存在誤差，這是理想化的有限元模型與現場復雜條件下所獲得的測試結果之間的差異所導致，主要有以下幾個因素：

1)現場實驗結果受到測試時間長短、儀器自身及溫濕度對應變片的影響而產生誤差；2)有限元自身的局限性：有限元模擬過程將實際工況進行簡化，無法完全模擬施工現場的實際情況；3)材料力學性能：鋼波紋板材質是非均勻的，且板件的拼接、加固等都會對拱橋產生影響，而采用理想化的有限元模型，就會造成波紋鋼實測和模型仿真結果存在一定的差異。

4 結語

通過研究波形對中小跨徑波紋鋼拱橋的力學性能的影響可以得出，隨著波距的增大，拱橋的撓度絕對值、切向應力絕對值及等效應力值均減小，且在拱腳及30°截面處波峰和波谷之間均存在明顯的彎矩。

在多種影響因素共同作用下，現場實測結果與鋼波紋板拱橋有限元模型模擬結果之間存在誤差，但誤差較小，因此采用有限元法模擬分析中小跨徑波紋鋼拱橋的受力情況是可行的。