基于譜表示法和時間衰變模型的巖體穩定性評價

吳川 廖坤陽 孫大齊

摘要：為了從時間尺度和空間變異性上研究石質文物危巖體的結構穩定性，建立了巖體強度參數的空間分布和時間退化模型。選取麥積山石窟13號窟危巖體為研究對象，利用強度折減法對石窟巖體穩定性進行模擬計算。模擬結果表明：① 麥積山13號窟現狀條件下最大位移為1.8 mm，中部位移方向略微傾向石窟外側，石窟頂部呈現局部塑性變形，但整體穩定性較好，模擬結果與現狀調查較為一致。② 加入時間衰變模型后發現，13號窟現狀條件下頂部位移為1.2 mm;預測50 a后洞窟最大位移位于洞頂，為1.3 mm;100 a后洞窟最大位移從洞頂轉移至坡腳，為16.7 mm。③ 強度折減分析表明，100 a后模型產生大面積塑性區域貫通現象，洞頂發生拉張破壞，洞底剪切破壞。時空變異模型有效提高了傳統靜力學計算精度，通過時間退化模型真實地再現了石窟危巖體的動態破壞過程，在精確評價危巖體長期穩定性方面具有廣泛應用價值，可為危巖治理提供參考。

關 鍵 詞：

麥積山石窟; 時空變異性; 非平穩隨機過程譜表示法; 危巖體穩定性; 石質文物

中圖法分類號： TU47

文獻標志碼： A

DOI：10.16232/j.cnki.1001-4179.2021.06.013

危巖體的穩定性評價和分析一直是巖土工程、地質工程領域的重要研究方向[1]。目前危巖體穩定性分析方法主要分為兩類：第一類以剛體極限平衡法為基礎，如陳洪凱等[2]將三峽庫區危巖體失穩破壞分為滑塌式、傾倒式和墜落式，并在考慮自重、地震和裂隙水壓力的情況下給出了3種危巖體的靜力學計算方法。第二類評價方法以數值方法（如限元法、有限差分和離散元）為基礎，如鄭穎人等[3]將有限元強度折減法應用于巖土邊坡穩定性評價中，開創了求解巖質邊坡滑動面與穩定安全系數的先河。前一類方法過于簡便。第二類評價法憑借計算機強大的運算效率劃分單元體進行穩定性評價，卻對于巖體性質的變異性考慮不足，如巖體參數（凝聚力、內摩擦角、重度等）在空間分布的不均勻性和時間上是不斷變化的。Symbol`@@石質文物由于遭受長年累月的風化侵蝕作用，整體穩定性問題是文物保護工作的重點，同時由于其文物屬性無法采取大量破壞性的工程防護措施，因此其在時間和空間尺度上的穩定性研究具有現實意義。

目前，考慮時空變異性的石質文物危巖穩定性評價的成果較少，大部分研究成果仍處于現象描述階段[4-7]。本文以麥積山石窟13號窟為研究對象，綜合以上研究成果，利用譜表示法所生成的隨機場來模擬巖體抗剪強度參數空間變化特征。作為一種嘗試，建立基于強度衰減規律的時間變化模型。借助有限元強度折減法動態分析了石窟危巖體穩定性，并針對性地提出了適用于石質文物保護的防治方案。

1 空間參數分布模型

各種成因的環境地質作用會導致巖體在空間分布上出現差異性[8]，如發育于巖體中結構面的幾何分布特征，對于巖體強度、變形和滲透性的影響不容忽視。由于巖體強度參數既具有變異性又具有相關性，無法用簡單線性函數表示，所以選擇非平穩隨機過程譜表示法進行模擬。譜表示法于1990年被Shinozuka等用于模擬生成隨機場。本文采用了梁建文[9]推導的非平穩隨機過程蒙特卡洛模擬的一個譜表示法，該方法產生的樣本函數能夠較準確反映巖體參數在水平方向的延續性與垂直方向上的變異性。

巖體強度參數是一個切實存在的變量（不能小于零）。依據摩爾-庫倫剪切強度準則可知，對于巖體穩定性影響最為顯著的參數是凝聚力和內摩擦角，而其他參數如容重、彈性模量以及摩擦角等空間變異性不明顯，對于巖體穩定性分析貢獻很小?？紤]到數值計算效率，本文假定其他參數恒為常量，選用二維正態分布的非平穩隨機場來表示基本符合模擬要求。二維對數正態分布表達式如下：

fx，y=exp{ln1+V2×

M-1i=0N-1j=0

σij[Vijθcosω1ix+ω2jy+

Wijθsinω1ix+ω2jy]+

lnμ-ln1+V22}（1）

式中：x和y為單元體空間坐標;V，μ為別為凝聚力和內摩擦角的標準差和平均值;σij為（iM+j+1）項的標準差;Vij（θ），Wij（θ）分別為相對獨立的標準正態分布隨機變量;ω1i，ω2j則分別為頻率坐標。

其中，σij的計算公式如下：

σij=4Sω1i，ω2jΔω1Δω2（2）

式中：S為單邊功率譜密度函數;Δω1，Δω2分別為頻率坐標軸的離散區間。

由于相關函數對于巖體結構穩定性指標影響不明顯[9]，對石質文物穩定性模擬中選擇計算量較小的二維指數函數作為相關函數：

ρx，y=exp-2xδx+2yδy（3）

式中：ρ代表自相關系數;x，y代表水平和垂直方向距離，m;δx和δy分別代表水平方向和垂直方向的波動范圍，m。

現場測定樣本越多，就越能模擬出與實際情況相近的空間分布情況，理論上此種模擬方法可以獲得無限接近于真實情況的解，但在實際中是不可能的。通過譜表示法，根據有限個關鍵點出測得的強度參數（c，φ）統計值進行隨機場模擬，從而反演出可能的巖土體強度參數空間分布情況是可行的。由于文章篇幅限制，具體過程可參見文獻[8]。

2 時間衰變模型

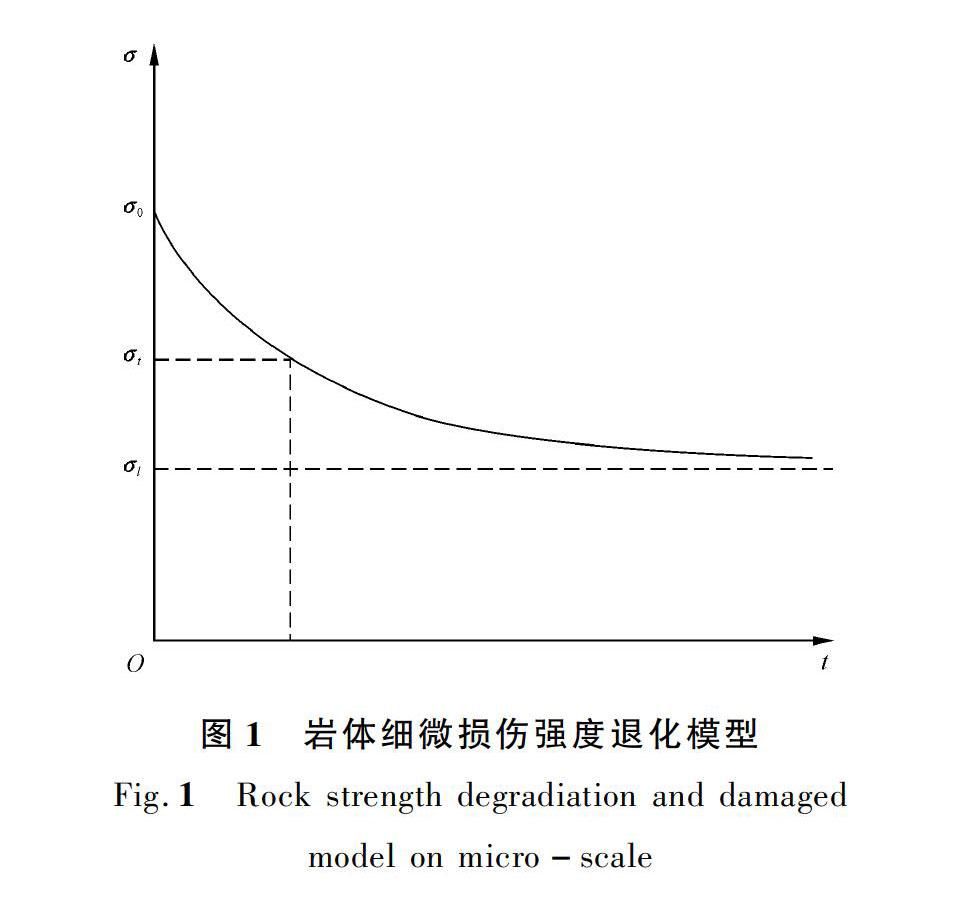
描述巖石力學特性隨時間變化的規律是危巖體穩定性分析中的難題，從時間尺度上評價巖體的穩定性研究尤為重要。許宏發等[10]通過實驗定量研究了軟巖的長期強度特征，認為巖體存在一組初始強度和最終強度，隨時間推移初始強度逐漸降低并無限接近于最終強度，導致這一變化過程是巖體內壁微觀損傷積累的結果。本文根據李連崇[11]關于巖體細微損傷隨時間變化試驗研究，嘗試建立了以指數衰減的力學退化模型（見圖1），用以描述危巖體的長期強度。

從圖1的退化模型中可知，巖體的強度（σt）隨時間逐漸衰退，初始強度（σ0）和長期強度（σl）固定不變;當t=0時，σt=σ0，當t→∞時，σt=σl。

由此將巖體微觀表征單元強度的時間退化模型用式（4）表示：

σt=σl+σ0-σle-kt（4）

式中：系數k和長期強度σl與巖體賦存環境有關。k反映強度衰減的快慢程度，若巖體所處環境有風化剝蝕、地震等劣化巖體結構的因素存在，那么系數k勢必會較大，同時σl的大小受環境條件與巖性條件共同控制。對于以上兩種量值的選取需根據現場和室內相關標定試驗來進行。

3 基于時空變異模型的評價方法

在將時間和空間變異模型加載之前，用強度折減法自動搜索滑動面，且應用數值模擬軟件對其穩定性進行分析[12-13]。本文將新鮮巖體和強風化巖體的強度指標作為初始強度σ0和長期強度σl。對于空間分布參數隨機場的模擬，選取麥積山石窟關鍵點的強度指標輸入譜表示計算法中，根據關鍵點強度參數分布規律，譜表示法反演出擬合最好的巖體整體空間參數分布情況。

（1） 基礎模型建立。首先在ANSYS中對模型進行剖分。通過程序轉換將建立好的三維模型導入FLAC3D。再在FLAC3D中對模型區域、邊界條件、材料屬性和模型等進行詳細設置。最后將完整的模型文件保存為后綴為xml的接口文件。

（2） 空間參數設定。根據所推演出的譜表示法模擬出不同方向（水平和垂直）波動范圍的隨機場，得到c和φ的n組隨機組合。然后將模型文件中的強度參數用以上n組數據替代，從而得到基于空間變異的新模型。

（3） 時間參數設定。根據強度隨時間衰變模型，將上一步所推導出的n組強度參數根據衰變公式折減后得n組新數據，基于這n組新數據的模型即為t時刻的危巖體三維模型，其具有時間和空間上的變異性。

（4） 穩定性計算。利用WinbatchTM（批處理軟件）賦值，在FLAC3D中對新模型文件的穩定性進行動態分析，得出計算結果。

4 算例分析

4.1 模型尺寸與網格劃分

采用三維激光掃描建立麥積山石窟的三維地形曲面。為了確保建模過程中模型不受網格離散化和建模范圍的影響，本文選取的模型范圍超過研究洞窟尺寸的2.5～3.0倍。依據三維激光掃描確定的模型曲面較為復雜和貼合實際情況，本文通過ANASYS采用四面體單元進行建模處理（見圖2），模型建好后導入到FLAC3D中進行數值分析。

由于麥積山石窟13號窟為南北向布置，為了便于計算，本文的模型坐標系設定豎直方向為Z軸，水平方向為X和Y軸，其中X軸正方向朝南，Y軸正方向朝東，石窟邊坡巖體走向與Y方向平行。最終確定模型尺寸為垂直方向（Z）高50 m，南北方向（X）長75 m，東西向（Y）長35 m。另外，考慮到石窟巖體表面性狀復雜，可能對后續的模型計算效率產生影響，因此本文對石窟中造像進行了一定程度簡化，并不影響石窟整體穩定性計算結果，簡化后的模型見圖2。

4.2 邊界條件與模型參數

模型計算過程中設定頂面和底面為自由邊界，模型南側（前側）同樣為自由邊界，側面和后面為固定約束。破壞準則參考摩爾-庫侖破壞準則。現場選取石窟基巖砂巖進行室內物理力學試驗。由于研究對象為石質文物，不宜進行大規模破壞性勘探，本文利用輕型便攜式鉆機沿石窟頂面進行鉆探，共布設鉆探剖面6條，鉆孔數量24個，鉆孔孔深2.0～5.0 m，通過對巖芯進行力學試驗發現弱風化巖體飽和單軸抗壓強度一般為30.0～40.0 MPa，強風化巖體一般為12.6～18.7 MPa，相較而言強風化巖體強度較弱風化強度衰減約38.1%～47.5%?，F場調查發現石窟巖體以弱風化和強風化巖體為主。模型建模所用巖體力學試驗結果見表1。

石窟模型在空間上的力學參數通過譜表示法來表征，根據有限個關鍵點測出的抗剪強度參數統計值進行隨機場模擬。由于巖體內變形模量、泊松比和密度空間變化不大，因此將其簡化為常量。本文通過現場鉆探取樣過程中確定的關鍵點的物理力學特性指標，將其換算成有關二維正態分布的函數值，其計算參數見表2。

4.3 模擬成果分析

4.3.1 現狀位移分布規律

將空間分布模型導入麥積山石窟模型力學參數中，用FLAC3D進行麥積山石窟的位移和應力分布規律分析，其模型的總位移矢量和等值線云圖見圖3。

由圖3可知，在自重應力作用下，石窟總體的位移呈現從頂部到底部均勻降低的規律：在山頂部最大位移為1.8 mm，中部位移方向略微傾向石窟外側，底部位移基本為0，說明該模型自重應力分布規律基本合理。

4.3.2 時間尺度預測

在石窟整體位移分析的基礎上，為了更全面分析和研究洞窟的時間衰變規律，對洞窟中間位置切割一處典型剖面，依據時間衰變模型設定強度衰減系數k為0.02，預測了13號窟隨時間的應力及位移變化規律。

圖4（a）為t=0現狀條件下的石窟中軸線剖面位移云圖，可以很明顯發現剖面的總位移方向向模型下后方傾斜，并且最大位移位于石窟頂部，其值為1.8 mm，平臺底部位移為0。13號洞窟頂部位移為1.2 mm，底部位移為0.6 mm，位移方向均為下后方。

圖4（b）代表t=50 a即50 a后的石窟剖面位移云圖。對比發現模型總位移呈增大趨勢，最大值0.3 mm，同時平臺底部位移依舊為0，說明該段時間石窟穩定性依舊較好。

當t=100 a時，模型頂部位移幾乎無變化，最大位移從石窟頂部轉移到底部平臺，石窟山腳的最大位移達到16.7 mm，13號洞窟頂板的沉降同樣達到13.7 mm，說明石窟已經發生了不同程度的局部失穩破壞?，F場調查情況發現，13號洞窟砂巖巖體受風化和裂隙滲水侵蝕較為嚴重，已經存在不同大小的風化凹槽，若不采取措施，可以預見100 a后石窟必然會發生一定程度的穩定性破壞問題。

模擬發現50 a內石窟山頂和山腳處應力集中尚不存在，但是隨著時間推移應力逐漸在兩個位置集中。在100 a后模型中山體向下應力逐漸增大，洞窟頂板和前壁洞口均發生了應力集中現象。

4.3.3 穩定性時空評價

加入空間參數分布模型和時間衰變模型后，強度拆減理論計算量大大超過傳統計算方式。因此本文將折減系數限定在1.0～3.0進行試運算。研究發現，當t=0，R=1.42時，模型頂部的局部區域開始發生塑性破壞，說明現狀條件下13號窟整體穩定性尚可，但是石窟頂部可能發生部分破壞。當t=100 a，R=1.10時，模型開始發生大面積塑性區域貫通現象。如圖5所示，在洞口上部黃色區域為大面積的拉張破壞，在洞窟底部紅色區域為剪切破壞，因此可以預測100 a石窟整體處于臨界破壞，隨時可能發生大規模的頂部巖體崩塌現象。

對于石質文物巖體的穩定安全性系數，目前并沒有統一的認識。參照現階段工程巖體邊坡相關規范，考慮到文物的價值屬性，石窟屬于重要保護文物，防治工程等級按一級考慮，危巖體防治安全系數應為1.40～1.60。目前來看13號窟整體處于穩定狀態。

5 結 論

（1） 巖體由于各種成因地質作用，其強度參數（c，φ）在空間分布上具有不確定性，而空間分布參數模型的引入克服了傳統靜力學計算中這一缺點，使得計算更加精確和符合實際情況。石質文物巖體由于巖體流變特性，其強度參數隨時間會逐漸降低，導致強度降低的主要因素是軟弱結構面受風化剝蝕等內外地質作用。時間衰變模型基于實際勘測成果從整體上把握了巖體強度衰變規律，預測了麥積山石窟13號窟長時間的穩定性，取得良好效果。

（2） 麥積山石窟現狀條件下最大位移為1.8 mm，石窟頂部呈現局部塑性變形，但整體穩定性較好，模擬結果與現狀調查較為一致;加入時間衰變模型后發現洞窟頂部位移為1.2 mm，預測50 a后洞窟最大位移位于洞頂，為1.3 mm，100 a后洞窟最大位移從洞頂轉移至坡腳，為16.7 mm;強度折減分析表明100 a后模型產生大面積塑性區域貫通現象，洞頂發生拉張破壞，洞底發生剪切破壞。

（3） 目前，將強度參數的時間和空間變異性結合起來評價巖體穩定性的研究尚處于初始階段。本文只是考慮了凝聚力和摩擦角的不確定性，對于重度、變形模量、邊界條件以及理論模型等假定其恒定不變，因此對于重要程度較高的復雜巖體，今后的穩定性評價應朝更精細、更復雜的方向發展。

參考文獻：

[1] 唐輝明.工程地質學基礎[M]北京：化學工業出版社，2008：15-21.

[2] 陳洪凱，唐紅梅，王蓉.三峽庫區危巖穩定性計算方法及應用[J].巖石力學與工程學報，2004，23（4）：614-619.

[3] 鄭穎人，趙尚毅.有限元強度折減法在土坡與巖坡中的應用[J].巖石力學與工程學報，2004，23（19）：3381-3388.

[4] 姜效璽，吳瓊，鄧小龍，等.復雜形態立柱式石質文物的病害調查及防治對策：以浙江省柯巖云骨巖柱為例[J].工程勘察，2016，44（10）：1-5.

[5] 甄剛，秦立科，馬宏林.乾陵無字碑裂隙分布情況調查及其穩定性分析[J].文博，2015（1）：94-98.

[6] 唐智亮.固結灌漿在保護云崗石窟石質文物遺址的應用研究[D].長春：吉林大學，2013.

[7] 田小甫.太原晉陽大佛邊坡巖體風化分級及地震穩定性評價研究[D].北京：中國地質大學（北京），2009.

[8] 潘別桐.巖體結構面網絡模擬及應用[M].武漢：中國地質大學出版社，1987：1-2.

[9] 梁建文，肖笛.非平穩隨機過程模擬的一個譜表示方法[J].應用概率統計，2005，21（4）：375-386.

[10] 許宏發.軟巖強度和彈模的時間效應研究[J].巖石力學與工程學報，1997，16（3）：246-246.

[11] 李連崇，徐濤，唐春安，等.單軸壓縮下巖石蠕變失穩破壞過程數值模擬[J].巖土力學，2007，28（9）：1978-1982，1986.

[12] 趙尚毅，鄭穎人，時衛民，王敬林.用有限元強度折減法求邊坡穩定安全系數[J].巖土工程學報，2002，24（3）：343-346.

[13] 向娟，陳占鋒，范文臣.考慮巖體節理密度影響的高陡邊坡穩定性研究[J].中國科技論文，2018，13（24）：2790-2795.

（編輯：鄭 毅）

Stability analysis on dangerous rockmass based on spectral representation

method and time degradation model

WU Chuan1，LIAO Kunyang2，SUN Daqi3

（1.Chongqing Industry Polytechnic College，Chongqing 401120，China; 2.Fujian Forestry Vocational & Technical College，Longyan 353000，China; 3.China Academy of Railway Sciences，Beijing 100081，China;）

Abstract：

In order to study the structural stability of stone cultural relic dangerous rock masses from time scale and spatial variability，a model of spatial distribution and time degradation of rock mass strength parameters was established.The dangerous rock mass of Grotto 13 in the Maiji Mountain Grottoes was selected as the research object.The strength reduction method was used to simulate and calculate the rock mass stability.The simulation results show that the maximum displacement under the current conditions of the Maiji Mountain Grotto 13 is 1.8 mm，displacement direction of the middle part is slightly inclined to the outside of the cave，and the top of the cave shows local plastic deformation，however the overall stability is good，and the simulation results are consistent with the current survey.By using the time degradation model，it is found that the top displacement of Grotto 13 is 1.2 mm under current conditions，and the maximum displacement of the cave is predicted to be 1.3 mm after 50 years，still locating at the cave top，however the maximum displacement of the cave will be transferred from the cave top to the slope foot after 100 years，reaching 16.7mm.It shows that the model will have a large plastic area penetration phenomenon after 100 years，top of the cave shows tensile failure，and the bottom of the cave shows shear failure.The spatio-temporal variation model effectively improves the accuracy of traditional static mechanicalcal culations，and the time degradation model truly reproduces the dynamic failure process of dangerous rock masses in caves.It has extensive application values in accurately evaluating the long-term structural stability of dangerous rock masses，and can be used as references for dangerous rock treatment project.

Key words：

Maiji Mountain Grottoes;spatio-temporal variability;spectral representation method of nonstationary random process;stability of dangerous rock masses;stone cultural relics