自緊式開口靜態封嚴密封環結構的設計及優化

程天馥 李雙喜 馬鈺虎 陳坤毅 施任杰

(北京化工大學機電工程學院 北京 100029)

從航空航天工程到化工機械制造，從醫藥設備研制到生活用品的包裝，密封結構無處不在。雖然通常密封元件在設備中占比很小，但其結構的可靠性直接影響著設備整體的運行情況及使用壽命[1]。中外相關領域的學者對各類密封結構進行了大量的深入研究，如刷式密封、干氣密封、迷宮密封以及應用于離心壓縮機上的各類密封等，并且取得了可觀的進展。由于航空航天領域的飛速發展，以液氫、液氧為燃料的火箭發動機越來越多地應用于其中，由于工作環境特殊，使得其密封結構必須同時具備耐低溫、耐高壓的能力[2-5]，因此金屬密封環應運而生。與普通密封環相比，金屬密封環更耐低溫，在高壓下變形更小，且可根據實際工況對密封環的形狀進行靈活的設計。目前常用的金屬密封環有C形、K形、X形、E形、W形、空心O形及U形等[6-9]。

針對金屬密封環的研究開始于1970年前后[10-11]。國外密封行業代表Parker公司所開發的BS密封結構具備很好的抗沖擊性能，開發的AF形密封結構則可以靈活地隨活塞桿移動。國內對金屬密封環的研究較晚，但也取得了許多成果[12]。我國專家學者開發出了很多具有代表性的金屬密封環結構，如適用于高溫高壓工況下的梯形截面靜密封結構[13]；動、靜密封均適用的改良Y形密封環[14]以及應用于環保系統中的非接觸式靜密封結構[15]等。

金屬密封環雖然有諸多優點，但仍存在很多的不足。通常金屬密封環的彈性都比較差，不易被壓縮，要想得到可靠的金屬密封結構，往往需要很大的密封預緊壓力，這在很多時候是無法實現的。另外，傳統的金屬密封環不適用于振動工況下，因其在振動工況下易于產生疲勞從而導致密封的泄漏。此外，金屬密封環對接觸面的表面粗糙度也有較高的要求。

本文作者針對金屬密封環不易壓縮、預緊力大、在振動工況下易于疲勞泄漏的缺點，優化設計了一種性能優越的自緊式開口靜態密封環結構。

1 自緊式開口靜態封嚴密封環模型的建立

文中所設計開發的自緊式開口靜態封嚴密封環(下文簡稱封嚴密封環)是在現有的金屬U形環[16]與V形環基礎上進行的改良優化。優化后的封嚴密封環同時具備良好的回彈性能與蓄能特性，能夠適應于低溫高壓及振動工況下。改進的封嚴密封環幾何結構如圖1所示，具體結構參數見表1。

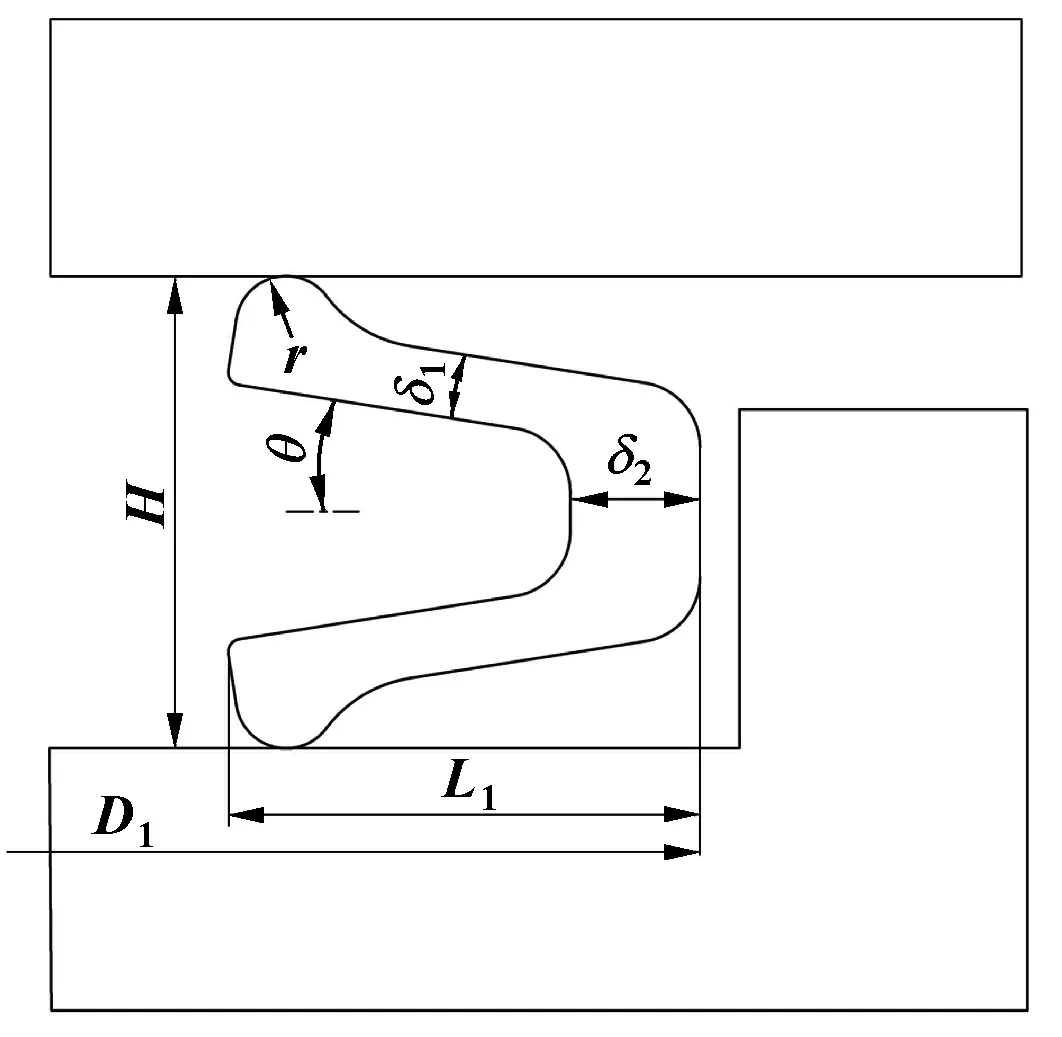
圖1 封嚴密封環的幾何尺寸Fig 1 Geometry of the sealing ring

表1 整體結構參數Table 1 Overall structure parameters

由于該封嚴密封環結構具有軸對稱性，為了降低計算難度，并提高計算準確性，利用有限元分析軟件ABAQUS建立一個二維軸對稱模型。該模型從上到下的結構依次為上法蘭、封嚴密封環、下法蘭，密封環兩端與法蘭分別摩擦接觸，結構詳圖見圖2。

圖2 密封環結構簡化模型Fig 2 Simplified structure model of the sealing ring

為了提高計算效率從而得到更為精確的結果，采用四邊形網格對模型進行劃分，所得網格劃分結果如圖3所示。共計網格數18 562個，經網格無關性驗證，該結果可靠。

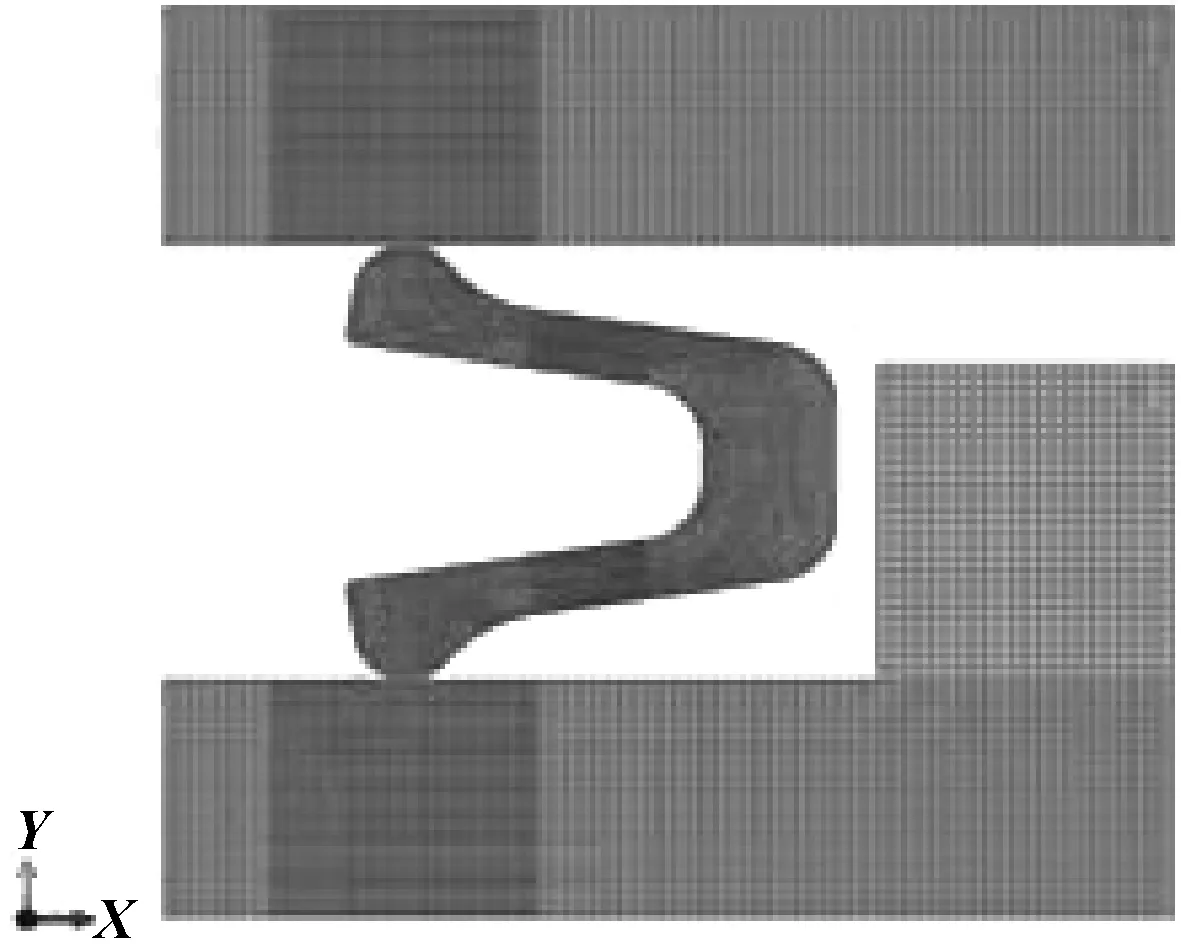
圖3 密封環網格劃分Fig 3 Mesh division of the sealing ring

封嚴密封環的材料為廣泛應用于航空領域的GH4169，該材料物理參數詳見表2。通過與常溫下相應數值對比可知，該材料在-183 ℃的低溫下具有優越的性能，故可以應用于低溫高壓環境下。

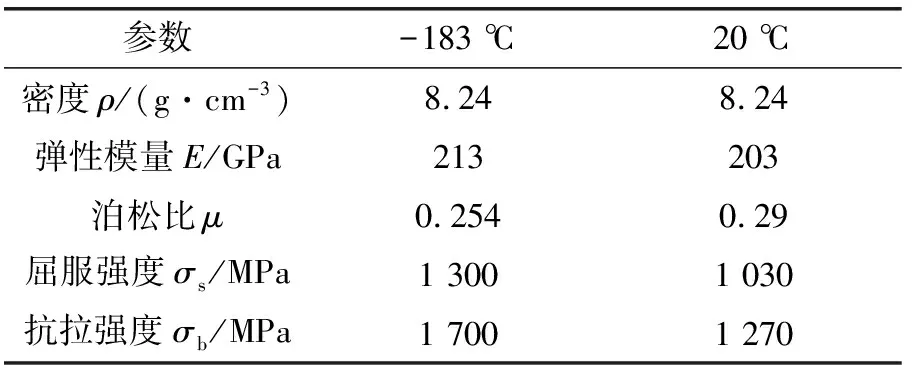
表2 GH4169材料參數

文中模擬所涉及的具體工況參數見表3，模型邊界示意圖為圖4所示，載荷施加情況見表4，圖5、6所示為應力及位移分析結果。

表4 邊界條件Table 4 Boundary conditions

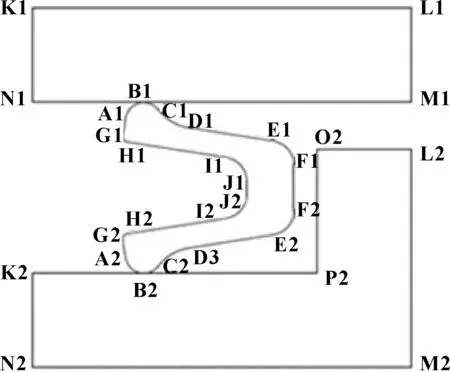
圖4 邊界條件加載Fig 4 Boundary condition loading

表3 工況參數

由圖5可知，應力最大值出現在封嚴密封環側壁與底壁連接的回轉位置處，數值較大，且存在應力分布不均現象；凸臺圓角與法蘭連接處也出現了較大的應力值，這對密封結構來說是十分不利的，應該通過相關結構的優化來降低應力強度。由圖6可知，在封嚴密封環與上法蘭邊界相接觸的凸臺處產生了位移最大值，考慮到密封環的彈性性能，應盡可能通過改變結構參數對其位移情況進行改良。

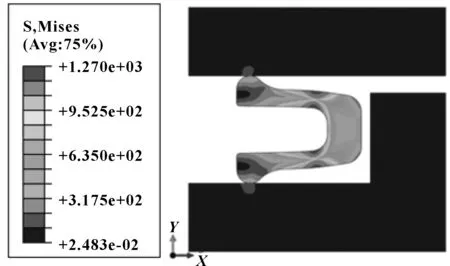
圖5 密封環應力云圖Fig 5 Stress cloud diagram of seal ring

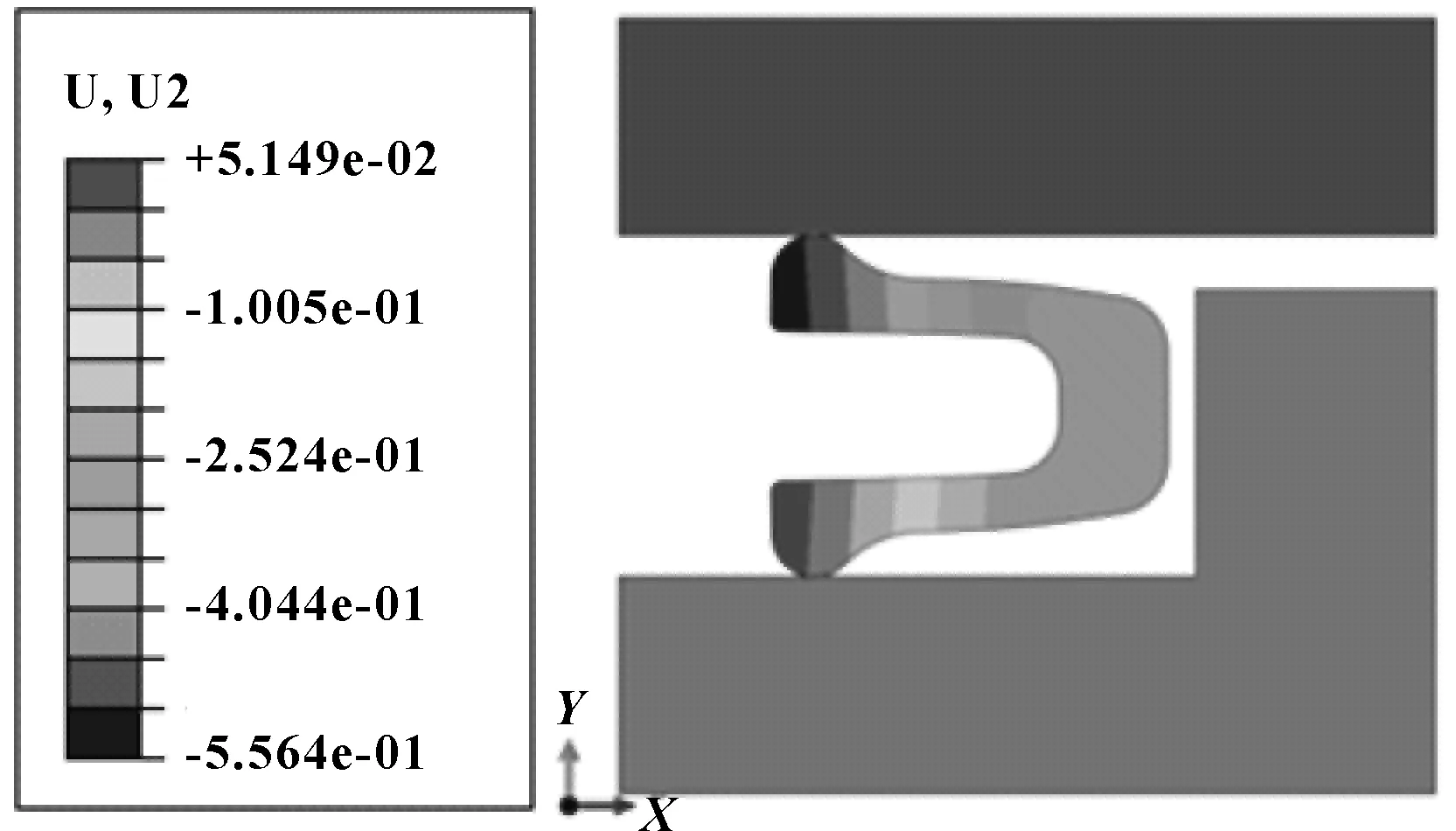
圖6 密封環位移云圖Fig 6 Displacement cloud diagram of seal ring

針對上述封嚴密封環存在的問題，文中分別研究側壁厚、底壁厚及凸臺大小等封嚴密封環主要結構參數對密封性能的影響，并對密封環結構進行優化。

2 封嚴密封環結構參數的優化設計

2.1 側壁厚δ1

〗封嚴密封環側壁與底壁相連，回轉處由于結構的不連續易產生應力突變現象，故所得應力結果數值較大。封嚴密封環在工作狀態下受到壓縮時，側壁為其提供彈力，側壁厚度發生變化時其所提供彈力的能力也不同。圖7(a)—(d)展示了封嚴密封環側壁厚對其最大Mises應力和位移、壓縮和回彈性能的影響關系。

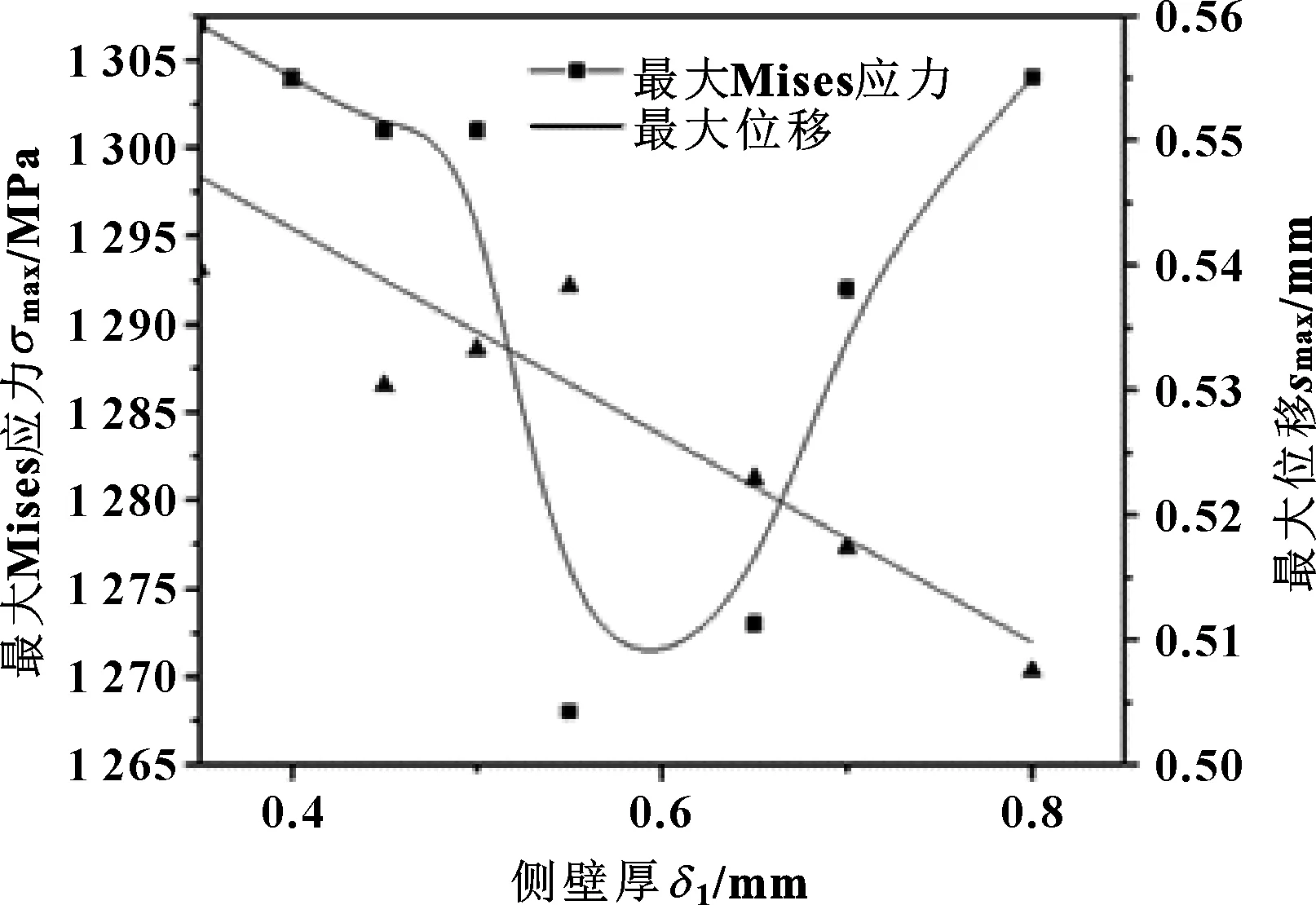
圖7(a) 最大Mises應力、最大位移隨側壁厚的變化Fig 7(a) Variation of maximum Mises stress and maximumdisplacement with side wall thickness

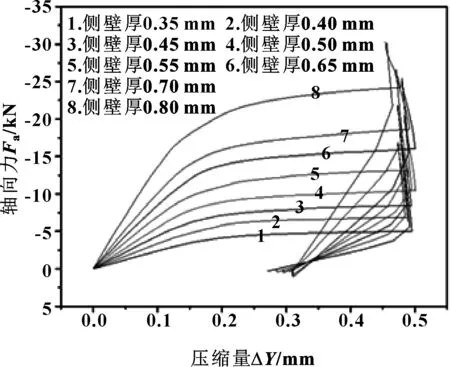
圖7(b) 不同封嚴密封環側壁厚下的壓縮回彈曲線Fig 7(b) Compression rebound curves atdifferent side wall thickness

圖7(c) 變形回彈率、自緊力增量比隨側壁厚的變化Fig 7(c) Variation of deformation resilience rateand self-tightening force incrementwith side wall thickness ratio

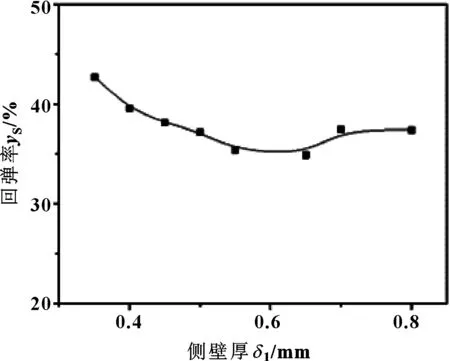
圖7(d) 回彈率隨側壁厚的變化Fig 7(d) Variation of springback rate with side wall thickness

圖7(a)顯示，在文中研究范圍內，封嚴密封環的最大位移隨側壁厚變化明顯，兩者近似呈負相關關系；當側壁厚從0.4 mm逐漸增大到0.8 mm時，封嚴密封環的最大位移下降了0.03 mm。封嚴密封環的最大Mises應力呈開口方向向上的拋物線狀，并在側壁厚為0.6 mm附近出現最低點。圖7(b)顯示，壓縮量相同時，側壁厚越大，封嚴密封環的軸向力越大。由圖7(c)及(d)所示，隨著側壁厚增加，密封環自緊力增量比呈下降趨勢，自緊效果下降。

綜合以上分析結果可知，封嚴密封環側壁厚的增大使其剛度增大，回彈力減小，回彈性能下降，故會產生更多不可回復的變形情況，密封環自緊效果下降。綜合考慮最大位移、最大Mises應力及回彈率等情況，封嚴密封環側壁厚最合適的范圍為0.4～0.45 mm。

2.2 底壁厚δ2

由于封嚴密封環底壁與側壁相連，但側壁受到一定的壓縮時，兩者相連處易產生較大應變從而發生斷裂情況，下面對封嚴密封環的不同底壁厚進行研究，其結果如圖8(a)—(d)所示。

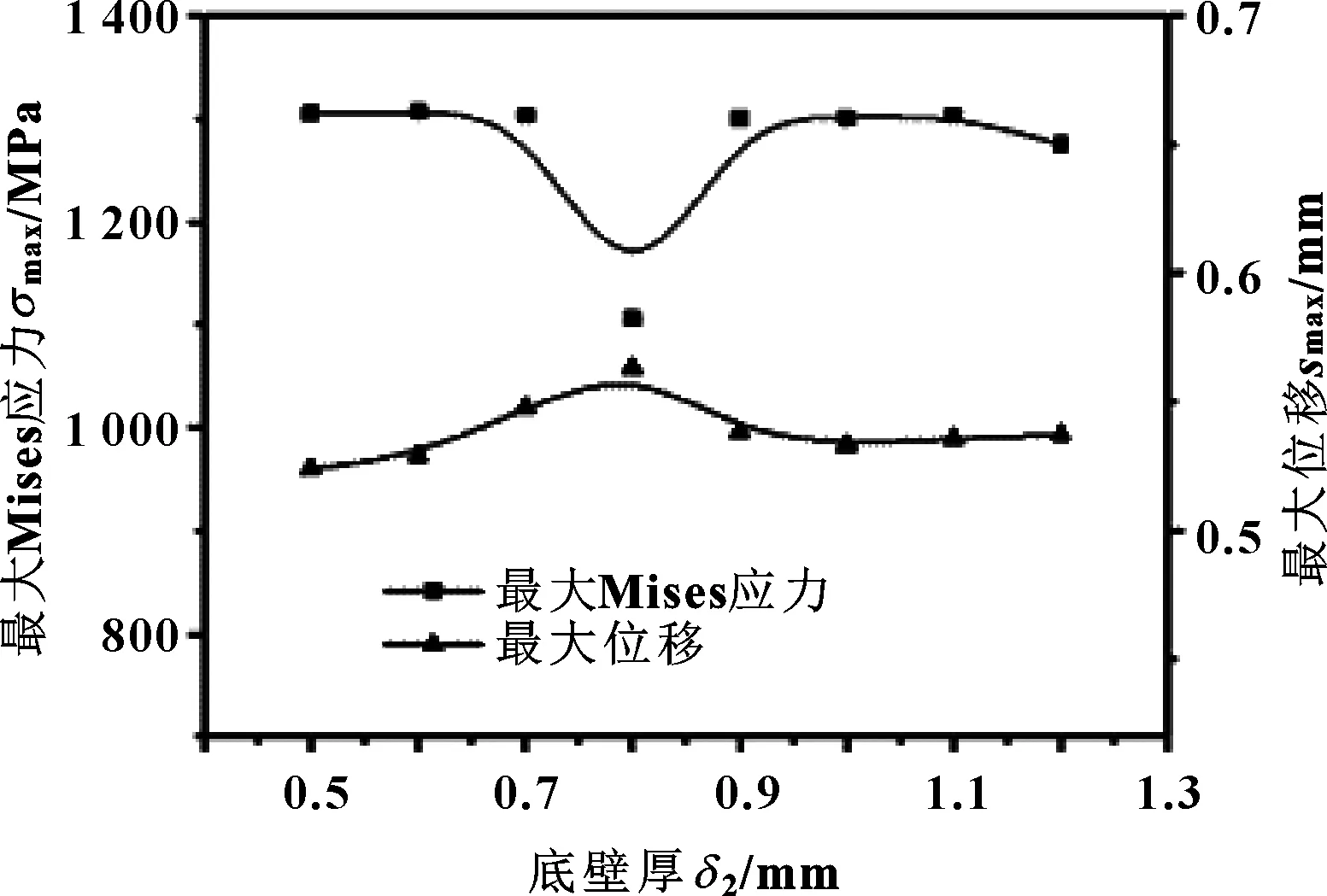
圖8(a) 最大Mises應力、最大位移隨底壁厚的變化Fig 8(a) Variation of maximum Mises stress and maximumdisplacement with bottom wall thickness

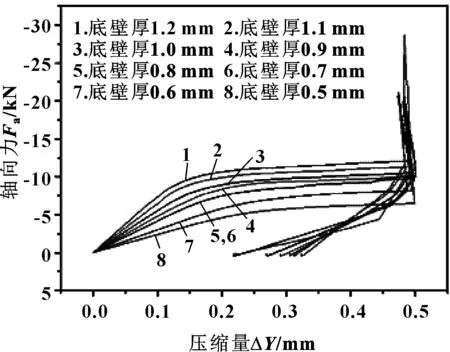
圖8(b) 不同封嚴密封環底壁厚下的壓縮回彈曲線Fig 8(b) Compression rebound curves at differentbottom wall thickness

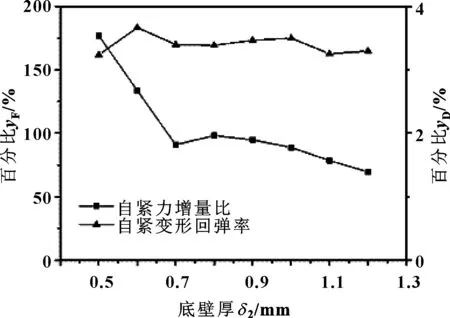
圖8(c) 變形回彈率、自緊力增量比隨底壁厚的變化Fig 8(c) Variation of deformation resilience rateand self-tightening force incrementwith bottom wall thickness

圖8(d) 回彈率隨底壁厚的變化Fig 8(d) Variation of springback rate with bottom wall thickness

由圖8(a)可知，封嚴密封環底壁厚對最大位移影響不大，隨著底壁厚的增加，最大位移波動幅度很小，最大Mises應力在底壁厚為0.65～0.9 mm之間呈現拋物線趨勢，在0.8 mm左右出現最小值。由圖8(b)可知，在壓縮量一定的情況下，密封環軸向力隨底壁厚的增大而呈上升趨勢，底壁厚的大小直接決定剛度的變化。圖8(c)、(d)可知，當底壁厚增大時，自緊力增量比先線性減小到一定值后波動不大，而回彈率曲線下降，回彈效果減弱。

綜合以上各分析結果得出，0.5～0.6 mm是封嚴密封環底壁厚的最佳取值范圍。

2.3 凸臺半徑r

由封嚴密封環裝配模型可知，凸臺結構與法蘭邊緣界面相接觸從而防止密封的泄漏，凸臺半徑的大小直接影響密封接觸面寬度。將封嚴密封環凸臺設計成球狀結構是為了更好地保證其與法蘭邊緣的線接觸，但凸臺半徑并不是越大越好，出于成本考慮，封嚴密封環凸臺半徑過大，將會造成結構的浪費，而且要求其他接觸面的精度很高，一旦不滿足，將發生密封的泄漏。封嚴密封環封最大Mises應力和位移、壓縮和回彈性能等隨凸臺半徑的變化曲線關系如圖9(a)—(d)所示。

由圖9(a)可知，隨著凸臺半徑在0.3～0.4 mm范圍內的增加，封嚴密封環最大位移變化甚微，略有上升;在凸臺半徑為0.39～0.4 mm之間時，最大Mises應力取得最小值，為1 220 MPa左右，其余數值基本在屈服極限附近。由圖9(b)可知，相同數據壓縮量的情況下，凸臺半徑越大，其軸向力越大，密封環的軸向剛度增加。由圖9(c)、(d)可知，凸臺半徑對自緊變形回彈率的影響較小，回彈率基本處于一個穩定的區間。

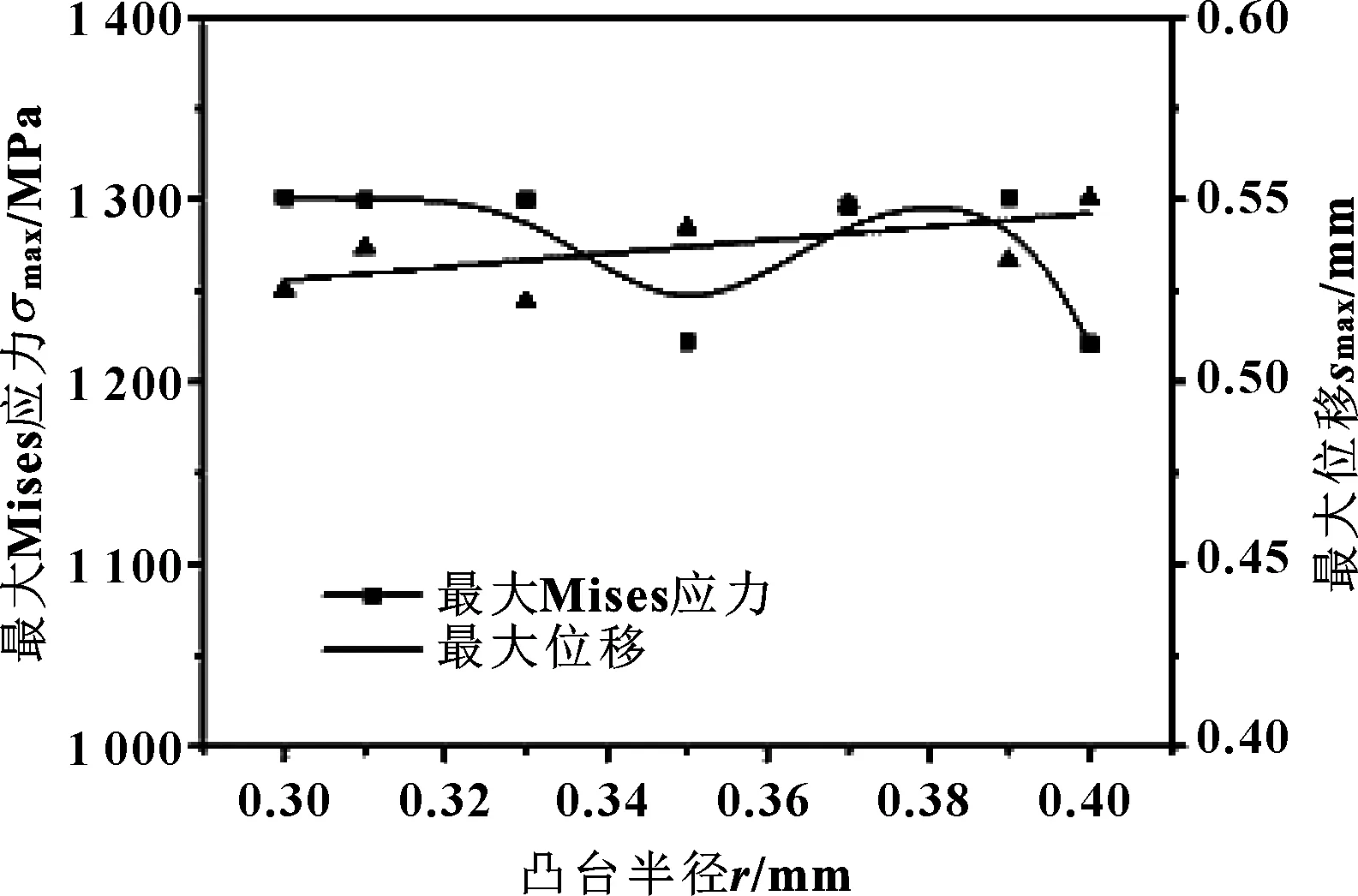
圖9(a) 最大Mises應力、最大位移隨凸臺半徑的變化Fig 9(a) Variation of maximum Mises stress and maximumdisplacement with boss radius

圖9(b) 不同凸臺半徑下的壓縮回彈曲線Fig 9 (b) Compression rebound curves at different boss radius

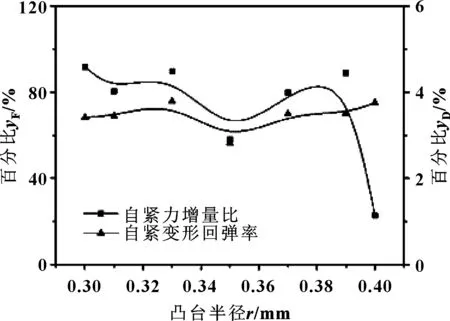
圖9(c) 變形回彈率、自緊力增量比隨凸臺半徑的變化Fig 9(c) Variation of deformation resilience rate and self-tightening force increment with boss radius ratio

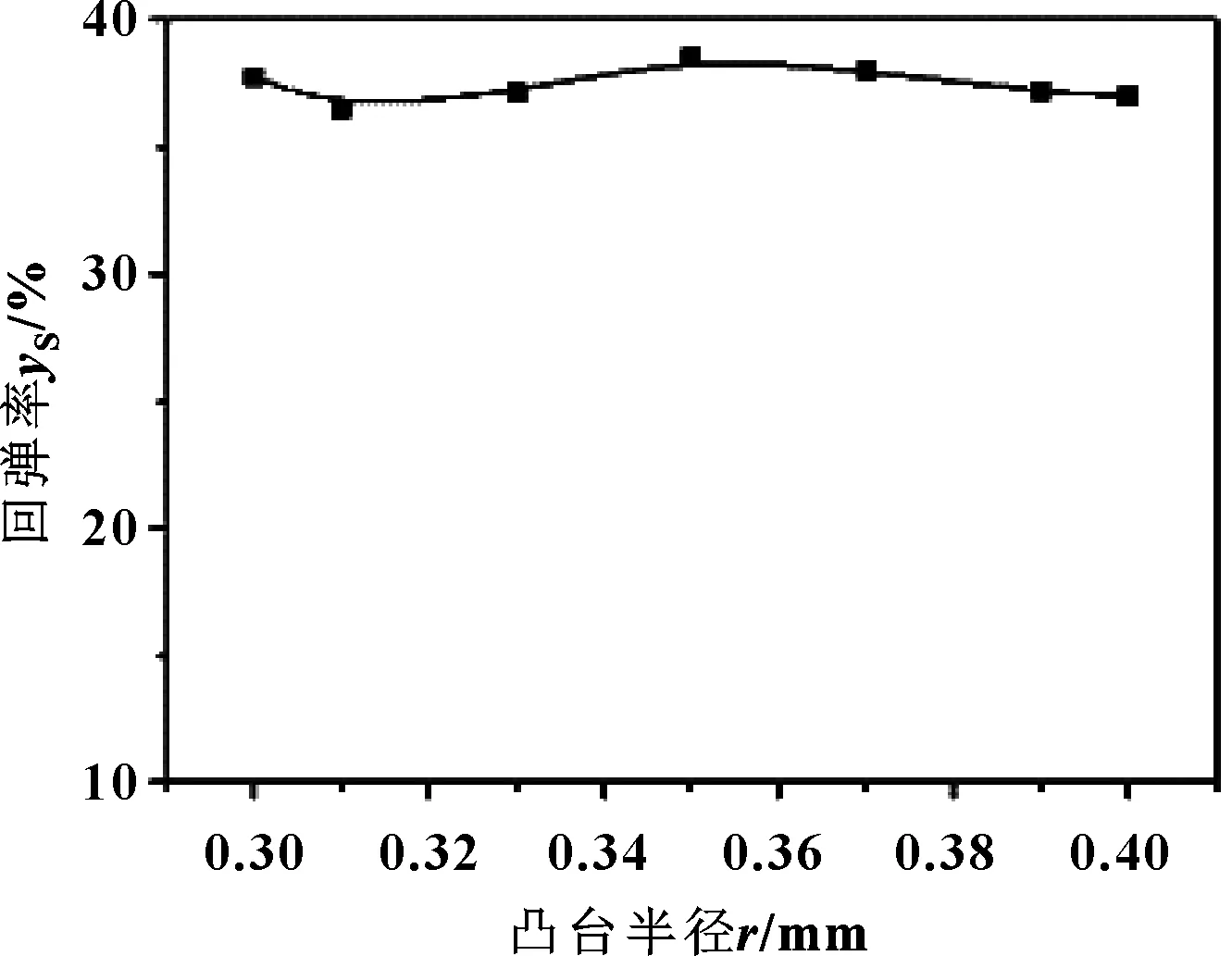
圖9(d) 回彈率隨凸臺半徑的變化Fig 9(d) Variation of springback rate with boss radius

綜合以上各性能變化，推薦封嚴密封環的凸臺半徑合理區間為0.30～0.33 mm。

2.4 傾斜角θ

封嚴密封環的傾斜角直接決定其開口尺寸的大小，當密封環受到壓縮時，傾斜角將產生彈力，不同角度所產生的彈力則不同，通過研究傾斜角變化對各參數的作用效果來確定最優的傾斜角范圍，所得結果如圖10(a)—(d)所示。

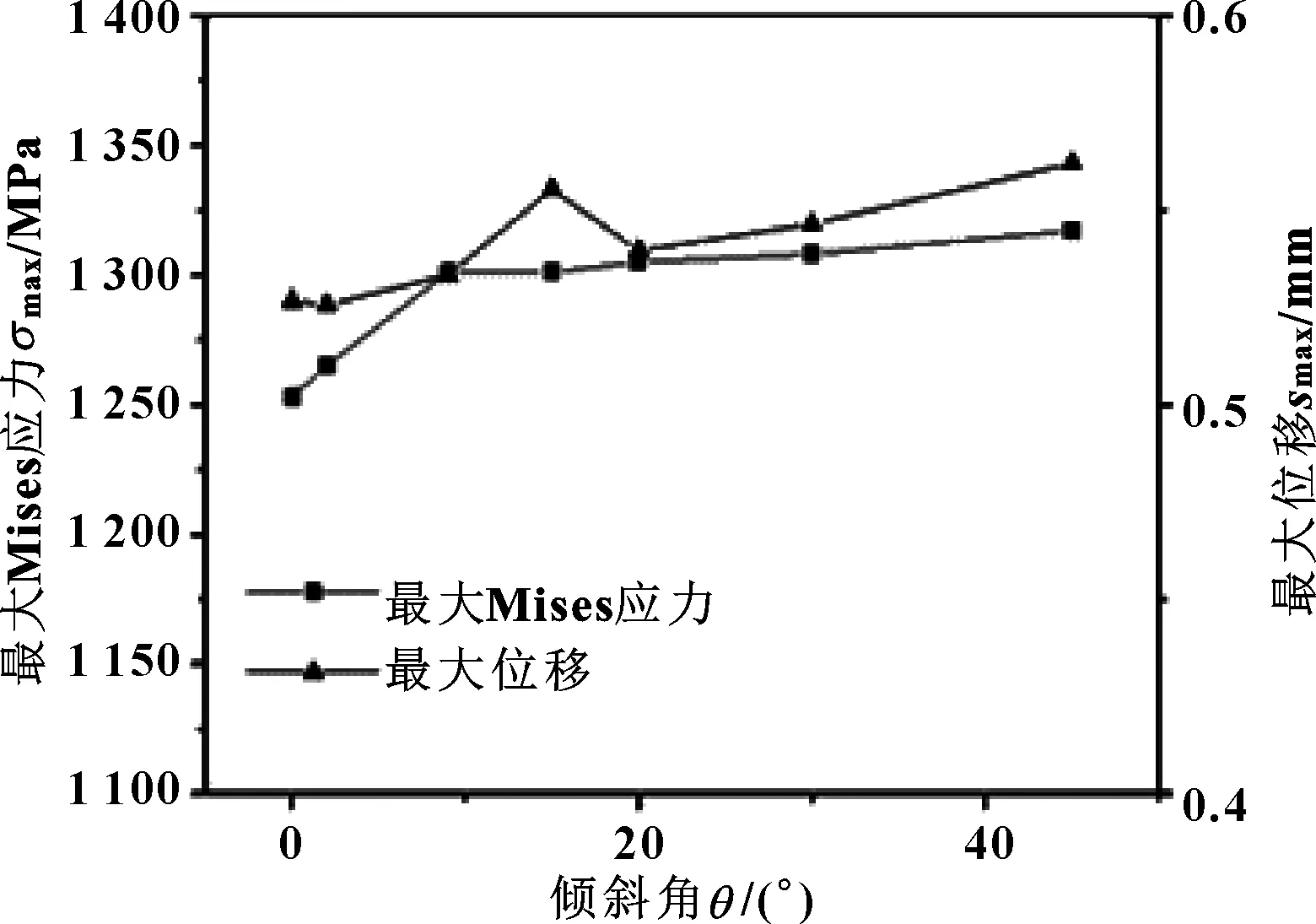
圖10(a) 最大Mises應力、最大位移隨傾斜角的變化Fig 10(a) Variation of maximum Mises stress andmaximum displacement with tilt angle

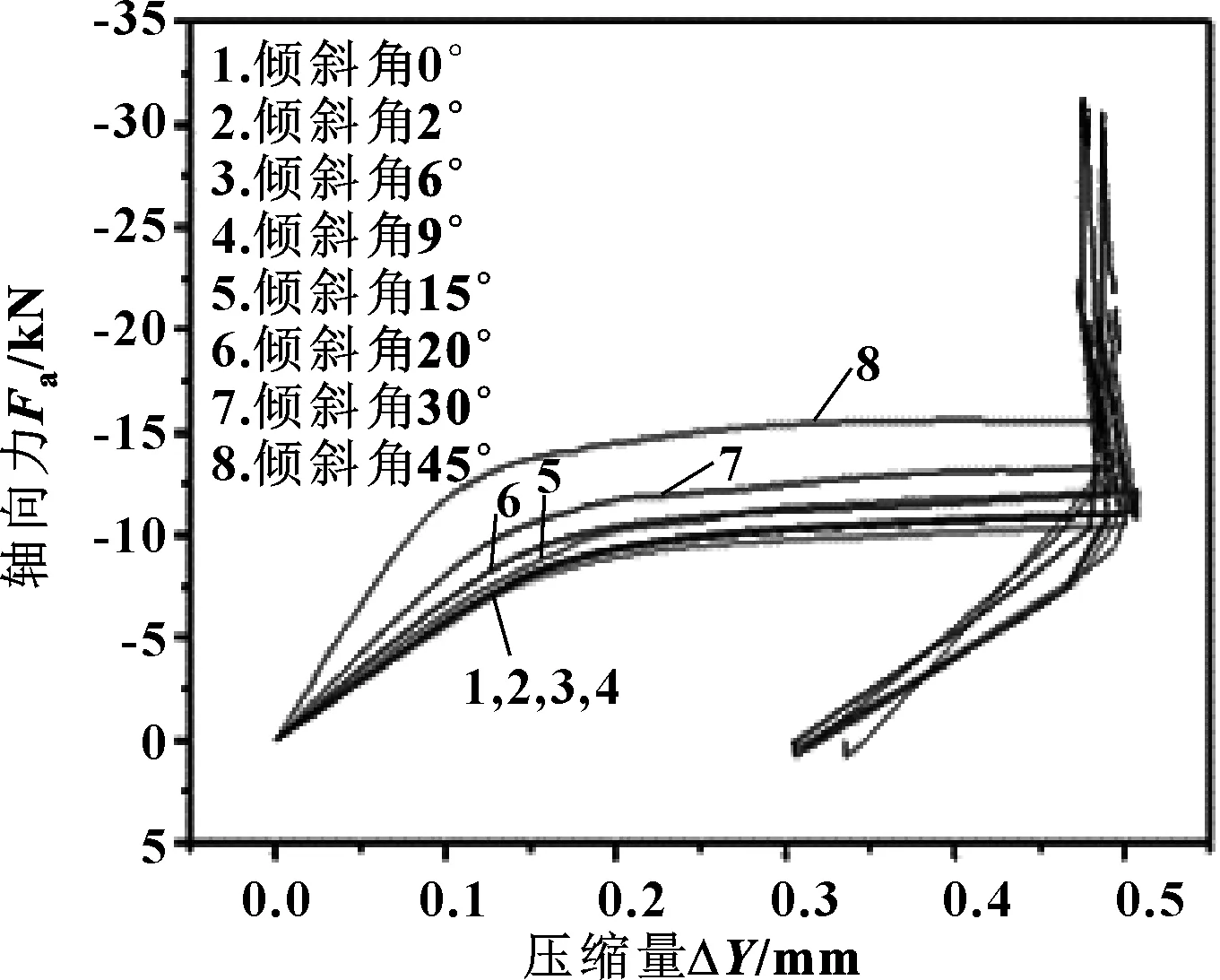
圖10(b) 不同傾斜角下的壓縮回彈曲線Fig10(b) Compression rebound curves at different tilt angle

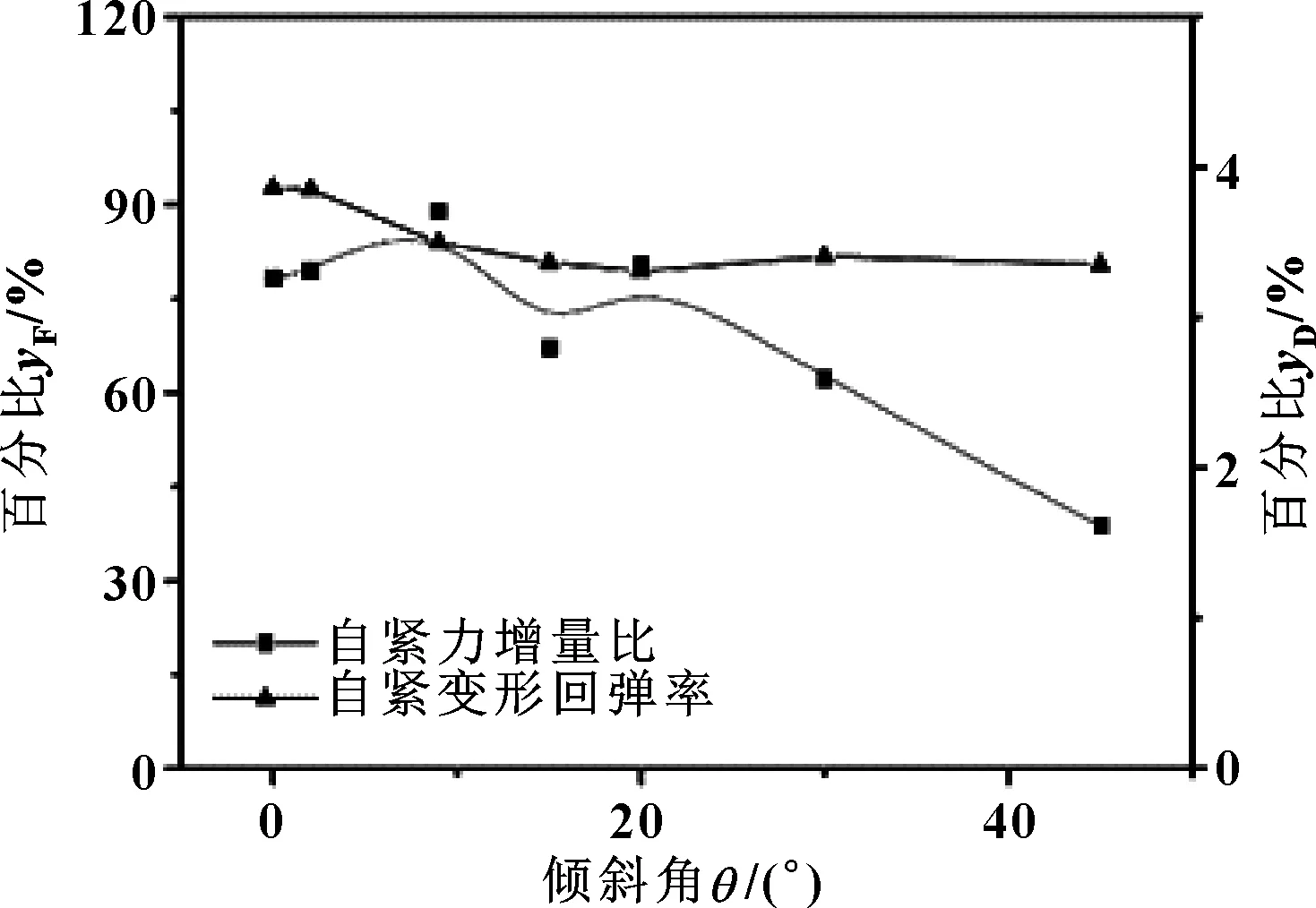
圖10(c) 變形回彈率、自緊力增量比隨傾斜角的變化Fig 10(c) Variation of deformation resilience rate and self-tightening force increment with tilt angle

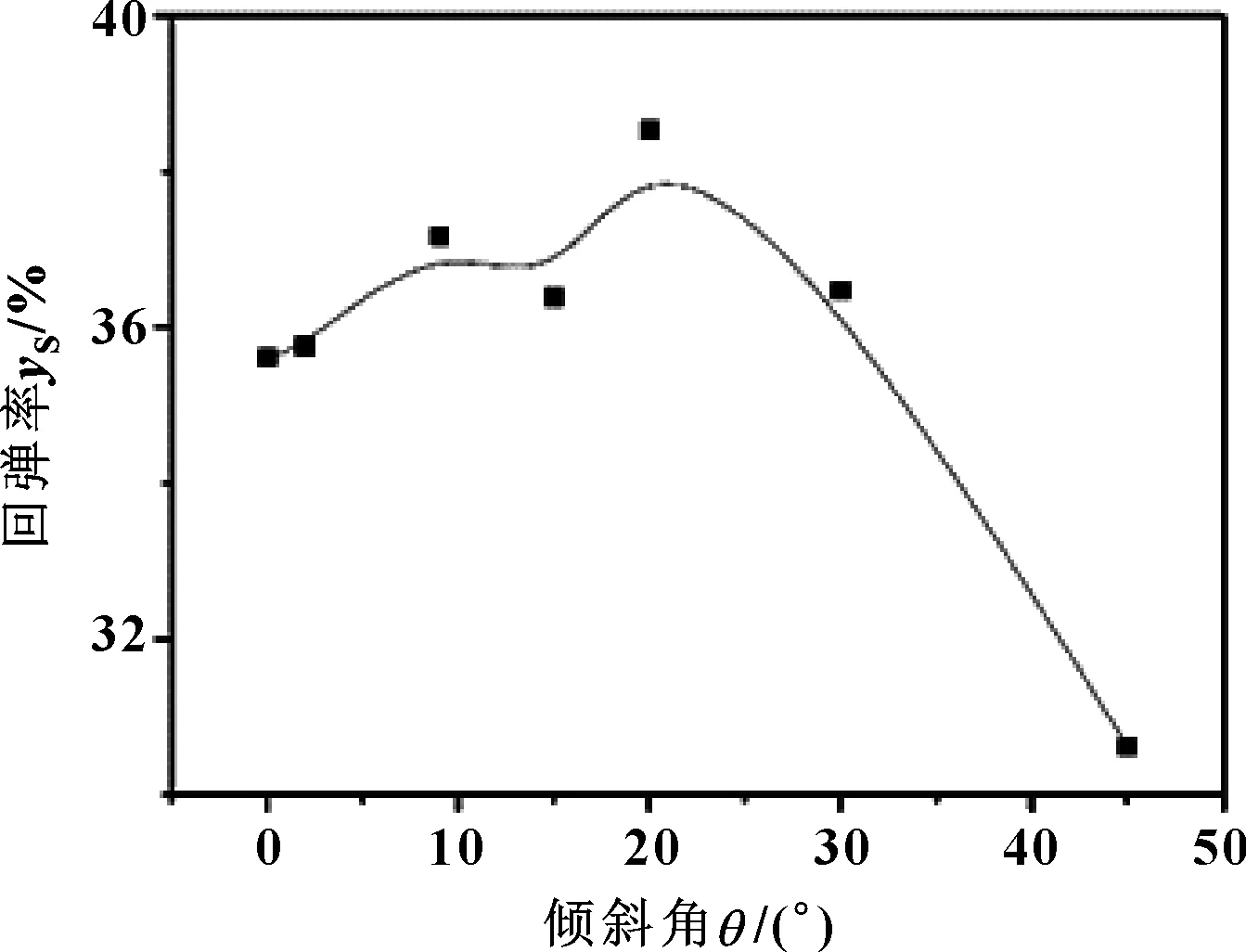
圖10(d) 回彈率隨傾斜角的變化Fig 10(d) Variation of springback rate with tilt angle

由圖10可知，當傾斜角逐漸增大時，封嚴密封環的最大Mises應力不斷增大，在0°～10°之間上升變化明顯，10°之后出現傾斜角的增大對最大Mises應力影響較小的情況；最大位移在15°時產生突變達到最大值，但曲線總體呈上升趨勢；在相同壓縮量下，封嚴密封環的傾斜角越大，其軸向力越大；回彈率隨著傾斜角的增大先呈現上升趨勢到20°左右時急劇下降。

綜合考慮上述性能變化，封嚴密封環的傾斜角推薦取值范圍是0°～9°。

2.5 密封環優化后的結果

通過上述分析，得到封嚴密封環主要結構參數的最優取值范圍為：側壁厚0.4～0.45 mm，底壁厚0.5～0.6 mm，凸臺半徑0.3～0.33 mm，傾斜角0°～9°。文中以密封環側壁厚0.42 mm、底壁厚0.55 mm、傾斜角8°以及凸臺半徑0.32 mm為例，對優化后密封環進行分析。

優化后的封嚴密封環應力云圖及位移云圖如圖11及圖12所示。對比優化前密封環的各云圖可知，優化后的封嚴密封環側壁與底壁回轉連接處應力強度明顯下降，且密封環上的應力分布更為均勻；在相同工況的壓縮量下，優化后的密封環位移數值更小，即相同工況下其產生的壓縮反力更大，更有利于阻止密封結構的泄漏。

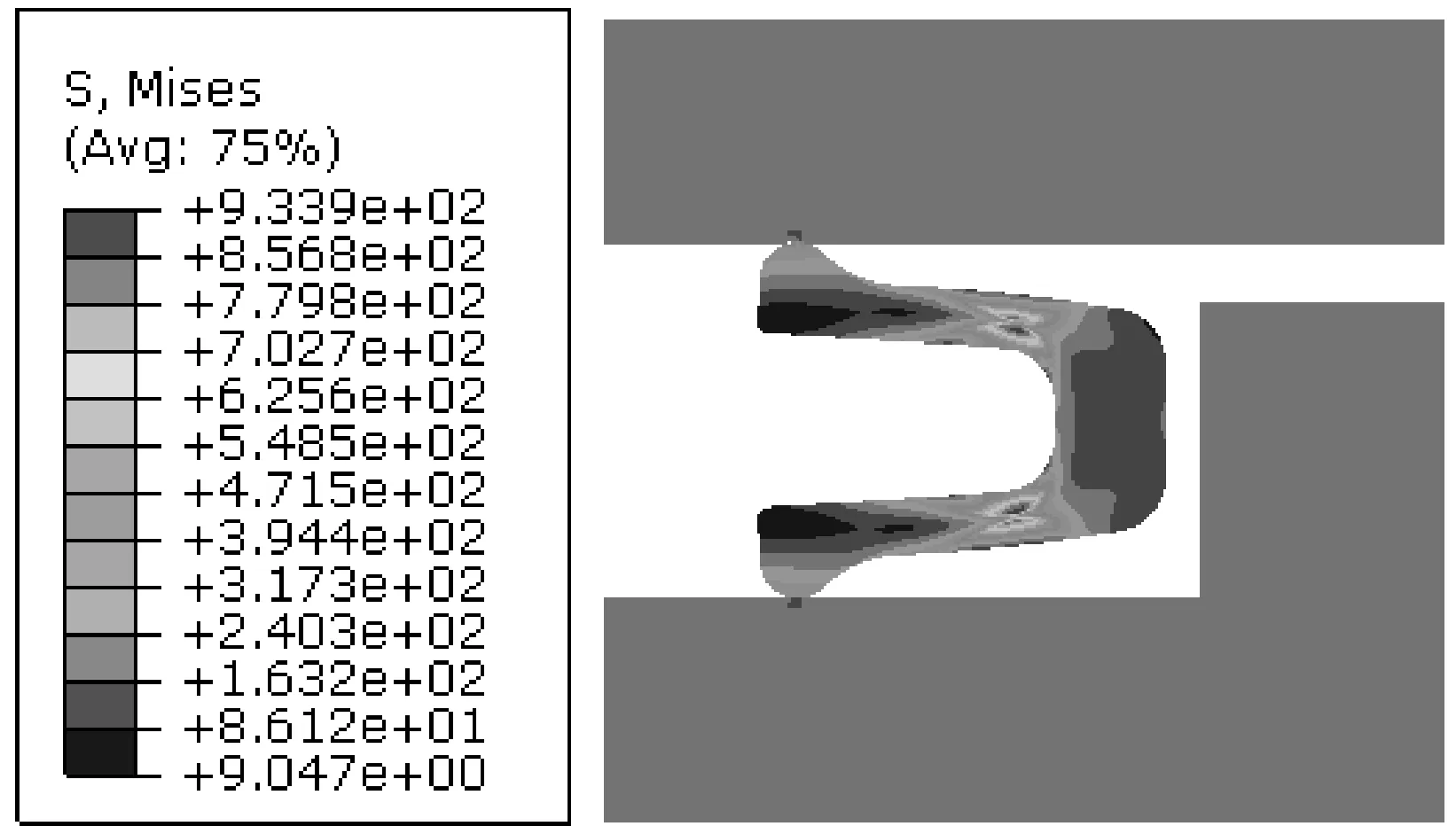
圖11 優化后密封環應力云圖Fig 11 Stress cloud diagram of the improved sealing ring

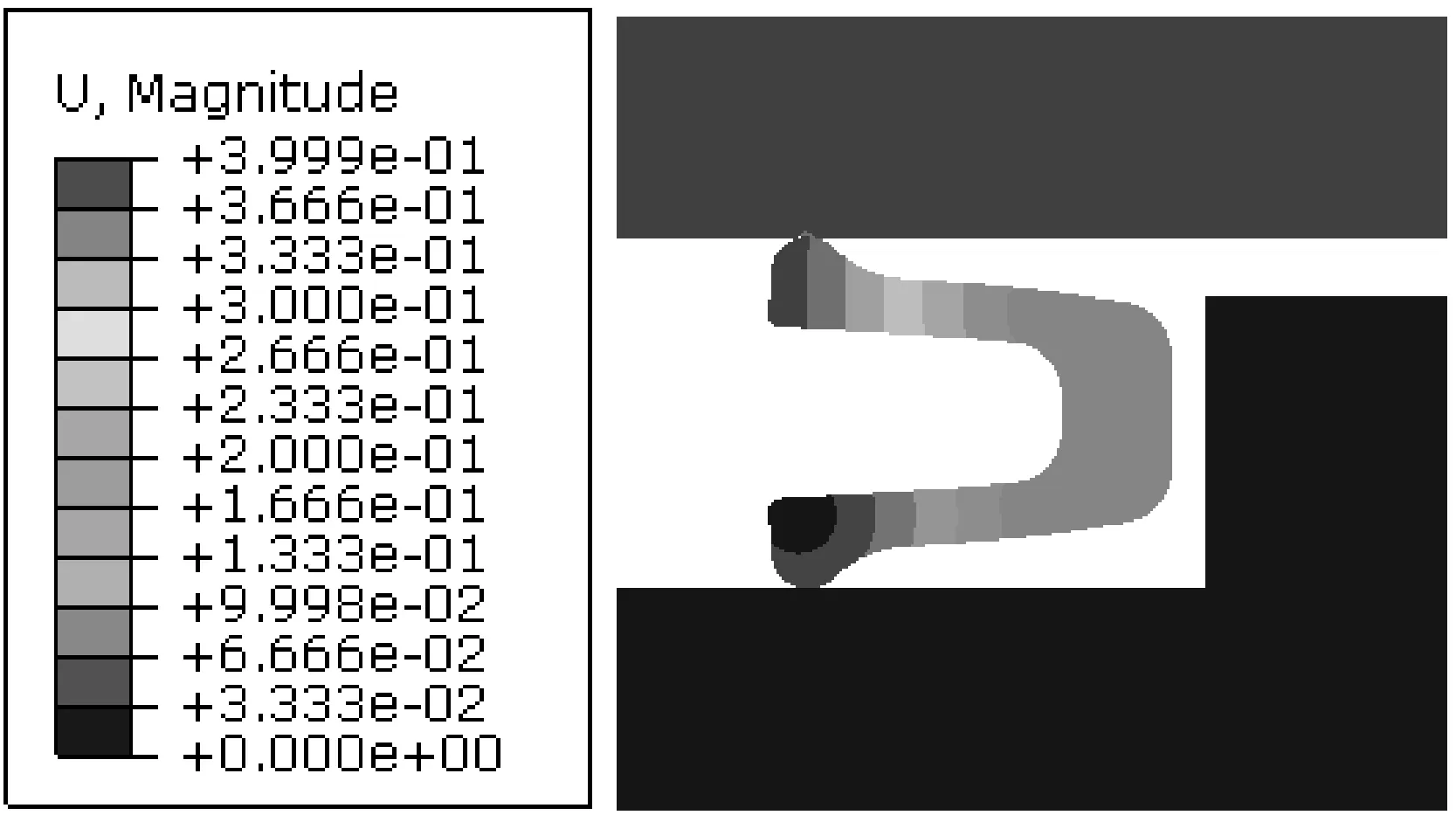
圖12 優化后密封環位移云圖Fig 12 Displacement cloud diagram of seal ring after improvement

2.6 試驗驗證

為進一步驗證文中模擬結果的準確性，分別對優化前后的密封環結構進行不同壓力下的泄漏量測試，所得泄漏量曲線如圖13所示。

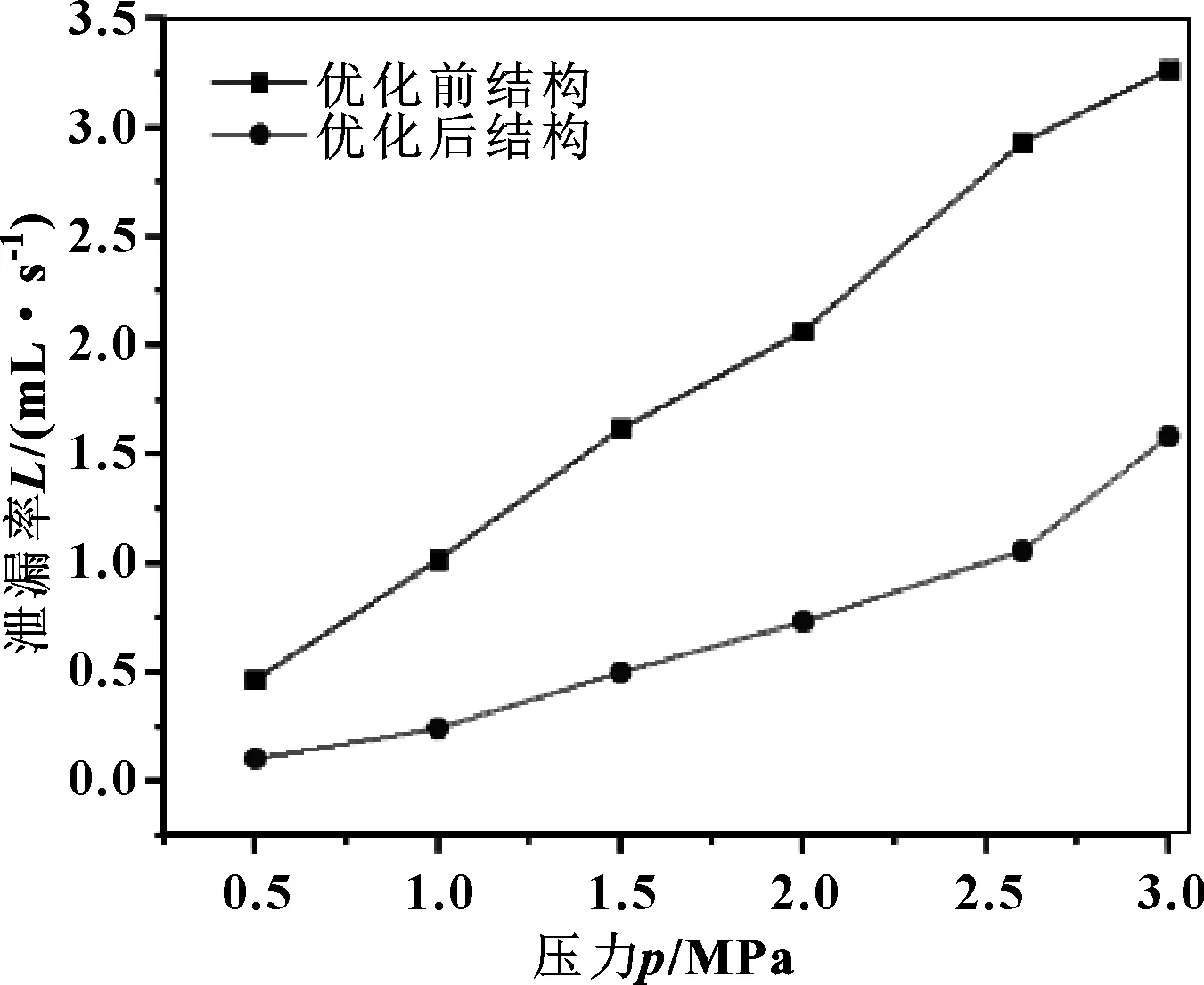
圖13 密封環優化前后泄漏量對比Fig 13 Comparison of leakage before andafter improvement of sealing ring

由圖13可知，優化前后密封結構的泄漏量均隨壓力的增大而增大，且變化趨勢基本一致，但在相同的壓力下，優化后的封嚴密封環結構的泄漏量遠遠小于優化前的結構，故可以驗證文中模擬結果的正確性。

3 結論

(1)應用有限元分析軟件ABAQUS建立自緊式開口靜態封嚴密封環二維軸對稱模型，通過控制變量法得到封嚴密封環取得較好密封性能時主要結構參數的取值范圍為：側壁厚0.4～0.45 mm，底壁厚0.5～0.6 mm，凸臺半徑0.3～0.33 mm，傾斜角0°～9°。

(2)封嚴密封環的側壁厚與底壁厚主要通過影響密封環的剛度來影響其回彈效果，回彈效果與二者數值負相關；密封環的回彈性能受凸臺半徑影響不大，傾斜角的變化對回彈率的影響較為明顯。

(3)綜合對比各參數可知，封嚴密封環最大Mises應力和最大位移的敏感參數是側壁厚。

(4)文中結果對自緊式開口靜態封嚴密封環的進一步研究優化具有指導意義。