基于靜力學分析的齒軌鐵路接觸軌中心錨結方案研究

李慶軍，關金發，陳俊卿，甘 磊，陳 展

0 引言

齒軌鐵路適合作為地勢起伏較大以及坡度較陡地區的一種交通形式，其主要特點是在列車轉向架中部裝有驅動齒輪，在坡道區段驅動齒輪與地面安裝的齒軌嚙合提升爬坡能力[1]。齒軌鐵路最早應用于1869年的美國華盛頓山齒軌鐵路[2]，國內的九寨溝、張家界以及七星山等地也正在準備修建齒軌鐵路。接觸軌是安裝于齒軌旁地面上的供電裝置，是齒軌鐵路牽引供電系統的重要組成部分[3]。一般的齒軌鐵路運用限制坡度為250‰，運行速度不高于40 km/h。在大坡度條件下，齒軌鐵路接觸軌的可靠性對列車安全運行起著至關重要的作用。 國內外學者對接觸軌系統做了大量的研究。文獻[4]基于ANSYS軟件建立集電靴與接觸軌直接 耦合的動力仿真模型；文獻[5]基于ANSYS Workbench對鋼鋁復合接觸軌溫度應力進行了有限元分析，得到不同工況下接觸軌溫度應力分布模型；文獻[6]推導了第三軌系統動力學耦合方程，基于Newmark算法研究了接觸軌結構的相關參數對受流質量的影響；文獻[7]基于SolidWorks Simulation有限元分析軟件，進行了接觸軌膨脹接頭在實際載荷下的受力分析及疲勞分析；文獻[8]基于接觸軌跨距情況、列車時速、靴軌作用力等不同條件，分別對接觸軌動、靜撓度進行分析研究，得到系統本身最大撓度情況；文獻[9]利用ANSYS有限元分析軟件分析了接觸軌預載變形與受流器模態，建立了受流器與第三軌耦合動力學模型，分析得出受流器慣性力對接觸壓力檢測影響較大的結論。目前，針對齒軌鐵路接觸軌系統的研究較少，針對大坡度情況下的接觸軌系統研究則更為少見。

本文針對大坡度齒軌鐵路接觸軌的中心錨結結構，采用有限元分析軟件ANSYS Workbench建立不同中心錨結結構的齒軌鐵路接觸軌模型，根據應力指標，評估齒軌鐵路3種不同接觸軌系統的結構可靠性，為齒軌鐵路接觸軌系統的設計與優化提供參考。

1 齒軌鐵路接觸軌模型

1.1 模型輸入參數

接觸軌系統主要由接觸軌、絕緣支架、尼龍墊塊、鋁軌接頭、中心錨結、螺栓、電纜連接板及膨脹接頭等組成[10]。絕緣支架包括本體、支座和卡爪。

考慮標準跨結構、中心錨結結構、線路坡度，建立跨距均為5 m的三絕緣支架式中心錨結、兩絕緣支架式中心錨結、兩絕緣支架帶斜拉桿式中心錨結3種250‰坡度齒軌鐵路接觸軌簡化模型，平面布置如圖1所示。仿真模型涵蓋接觸軌、中心錨結、鋁軌接頭、絕緣支架、尼龍墊塊等常用裝置及零部件。

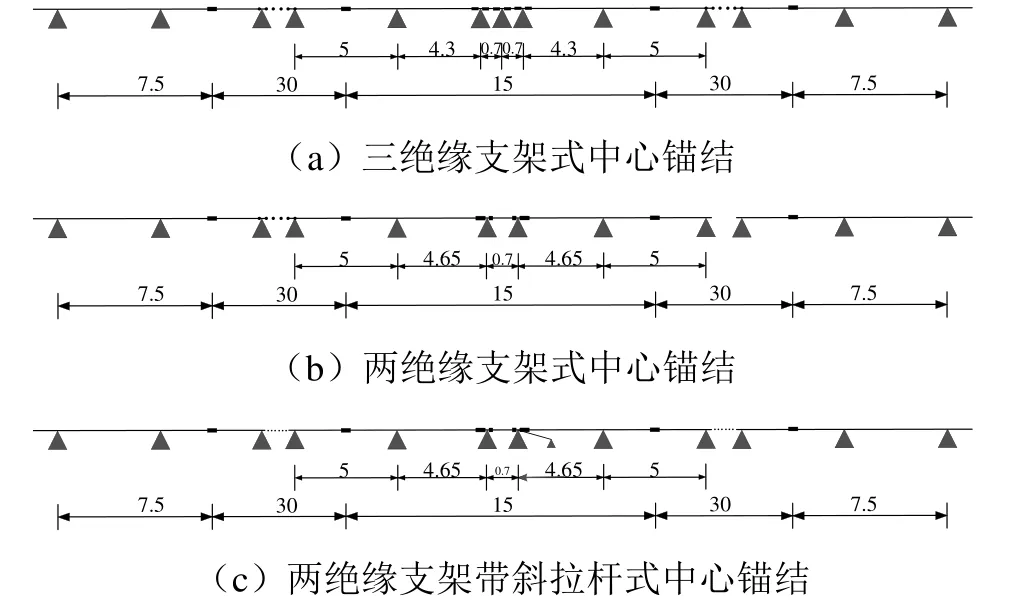
圖1 250‰坡度齒軌鐵路接觸軌平面布置（單位：m）

為簡化齒軌鐵路接觸軌仿真的冗余計算，提高運算效率，在建模過程中采用如下簡化原則：（1）不考慮螺栓連接件安裝不當對系統造成的影響；（2）不考慮拉出值對靜力學分析帶來的影響。

1.2 三維模型建立

齒軌鐵路接觸軌模型需進行合理簡化，該簡化方式以保留原有基本力學結構為原則。

對支持結構的簡化包括：（1）使用“工”字型元件代替絕緣支架上的螺栓結構；（2）忽略一些不規則的微小突起或凹陷。

對懸掛結構的簡化包括：（1）使用“工”字型元件代替接觸軌、中心錨結和鋁軌接頭中的螺栓結構；（2）忽略一些不規則的微小突起或凹陷。

基于以上的結構簡化，建立的齒軌鐵路接觸軌模型包含接觸軌、中心錨結、鋁軌接頭、絕緣支架等，如圖2所示。

圖2 接觸軌簡化模型

本文的3種模型均可等效為一段標準跨模型，模型長度90 m，跨距5 m，包含5段完整的15 m鋁軌、2段7.5 m鋁軌、1段中心錨結和6段鋁軌接頭。

中心錨結結構有3種：（1）三絕緣支架式，如圖3（a）所示，兩絕緣支架間距為0.7 m，每個支架左右各設置1個中心錨結，共6個中心錨結，每個中心錨結的長度為200 mm；（2）兩絕緣支架式，如圖3（b）所示，由2個絕緣支架和4個中心錨結組成，兩支架間的中心錨結長度為100 mm，外側的中心錨結長度為200 mm；（3）兩絕緣支架帶斜拉桿式，如圖3（c）所示，該結構在兩絕緣支架式中心錨結基礎上加裝了1根斜拉桿，用以抵消大坡度下接觸軌沿線路方向的重力載荷分量。

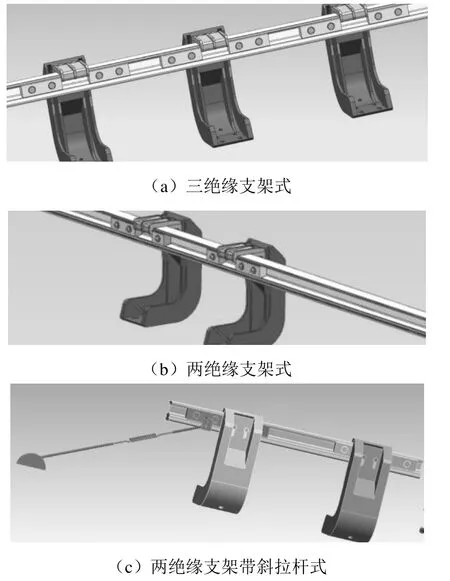
圖3 中心錨結結構

1.3 有限元模型建立

有限元分析是當前在復雜微分方程近似解求取過程中最為行之有效的方法之一，其通過離散化方法實現將連續體或結構體的求解域劃分成單元或子域，然后將其邊界的節點進行互相結合從而構成組合體。

基于齒軌鐵路接觸軌模型，利用有限元的方法進行仿真計算，建立相應的有限元模型。為模擬齒軌鐵路接觸軌實際受力情況，設置以下條件：（1）采用“工”型圓柱體代替絕緣支架上的螺栓結構，在“工”型圓柱體兩端施加壓力代替擰緊力，如圖4所示，其余結構中的螺栓結構采用粘連結構代替；（2）刪除模型中的彈簧，在有限元模型中的相應位置設置彈簧約束。

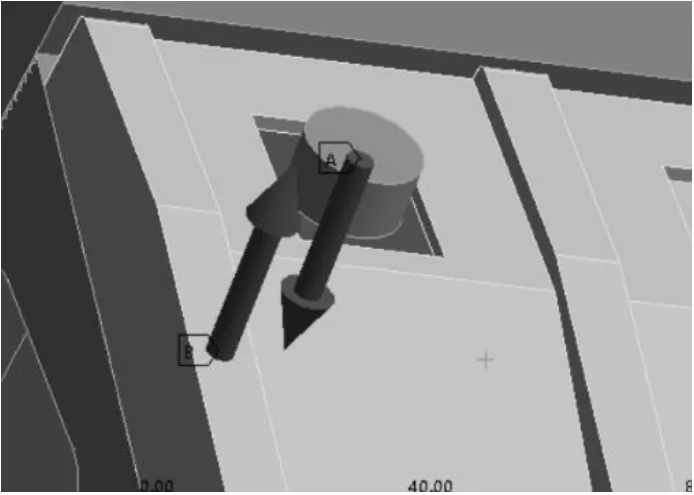
圖4 螺栓擰緊力

根據相關規定，螺栓力矩大小與公稱直徑要求如表1所示。由此可得：絕緣支架卡爪處采用M12螺栓，軸向力選用23 333 N；絕緣支架支座處采用M10螺栓，軸向力選用12 500 N。

表1 螺栓力矩與軸向力

齒軌鐵路接觸軌模型中主要材料參數按照表2定義。

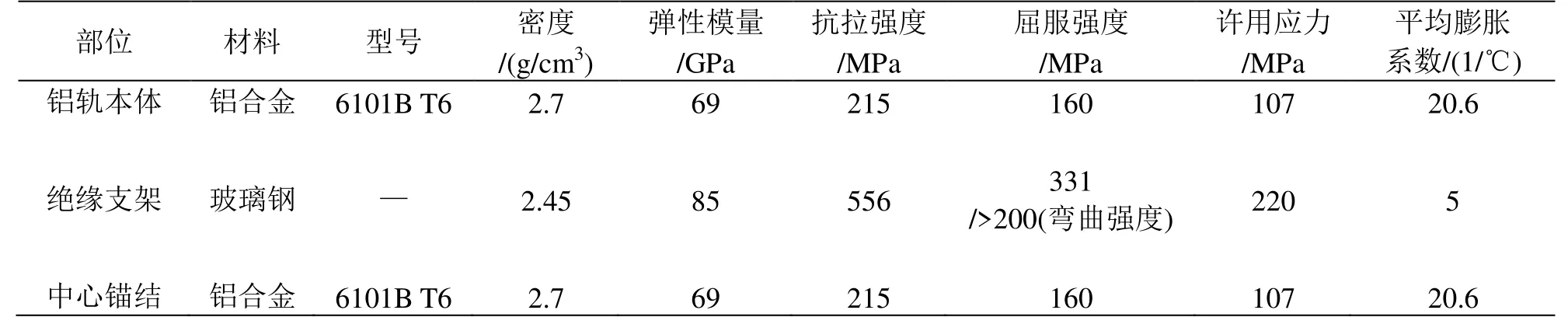
表2 材料參數

為提高網格質量，降低運算成本，本模型忽略了一部分圓角、圓孔和螺栓結構，對應地使用直角、平面和布爾連接的方式進行重新建模。模型選用50 mm為默認單元劃分有限元網格，對于小尺寸或重點關注的零部件，采用更小的網格劃分，以獲得更加精細的計算結果，并對絕緣支架、中心錨結和鋁軌接頭進行更精細的網格劃分。有限元網格劃分結果如圖5所示。

圖5 有限元網格劃分結果

1.4 評價標準

通過有限元仿真，得到齒軌鐵路接觸軌系統中各類零部件在不同工況下的應力狀態，分別與允許最大許用應力進行對比，評價齒軌鐵路接觸軌系統的靜力學結構是否具有較大的承載能力，是否滿足安全可靠使用的要求。

采用許用應力法對齒軌鐵路接觸軌系統中所有零部件進行應力狀態分析。零部件采用的材料不同，其許用應力也有差異，具體零部件的許用應力見表2，其中安全系數（材料屈服強度與許用應力的比值）取1.5。

2 靜力學仿真計算與分析

為校驗齒軌鐵路接觸軌系統的結構強度，對3種齒軌鐵路接觸軌有限元模型進行靜力學仿真，對比5 m跨距、250‰坡度下中心錨結采用三絕緣支架式、兩絕緣支架式以及兩絕緣支架帶斜拉桿式結構的接觸軌零部件受力情況，并評估不同接觸軌中心錨結方案的靜力學結構是否滿足安全可靠的使用要求。

2.1 三絕緣支架式中心錨結

在標準環境溫度（22 ℃）下，對250‰坡度、5 m跨距和三絕緣支架式中心錨結的齒軌鐵路接觸軌系統在承受自重載荷情況下進行靜力學仿真，發現應力集中的部位在中心錨結所在絕緣支架的支座與本體的交界面處，最大應力為35.011 MPa，中心錨結處最大應力為18.829 MPa，如圖6所示。

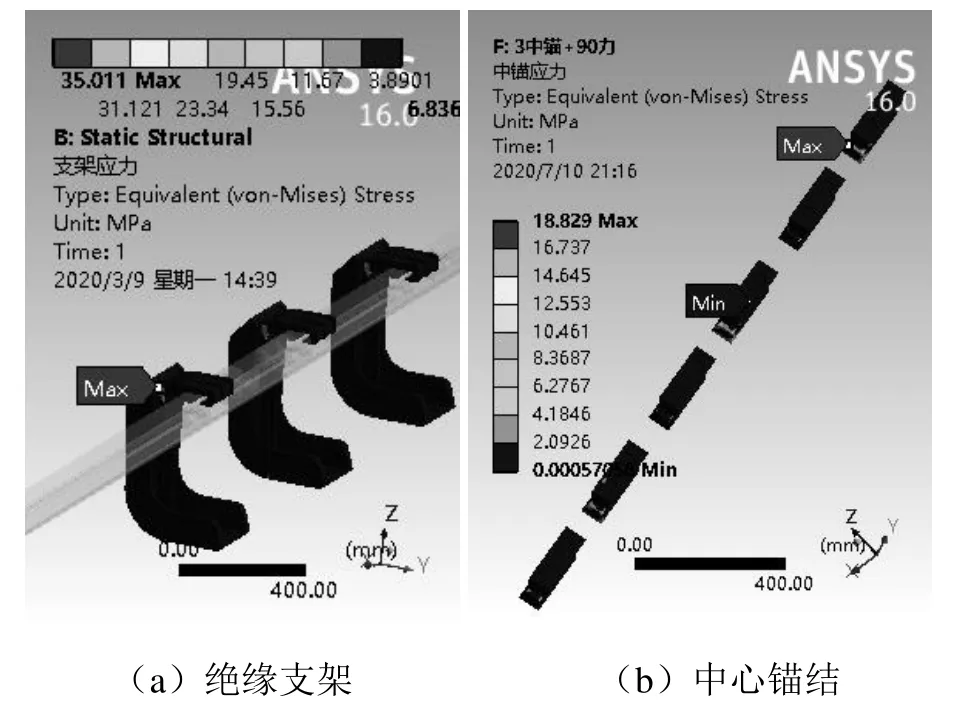
圖6 三絕緣支架式中心錨結應力狀態

經分析，主要是由于沿線路方向的接觸軌重力載荷分量通過中心錨結傳遞給卡爪，再傳遞給支座，在支座處產生了很大的彎矩；又由于支座表面呈鋸齒狀，支座與支架本體的接觸面積小，導致在支座表面出現明顯大于其他部位的應力。

2.2 兩絕緣支架式中心錨結

在標準環境溫度（22 ℃）下，對兩絕緣支架式中心錨結的齒軌鐵路接觸軌系統在承受自重載荷情況下進行靜力學仿真，結果表明應力集中部位與三絕緣支架式中心錨結相同，絕緣支架處最大應力為225.63 MPa，中心錨結處最大應力為73.839 MPa，如圖7所示。

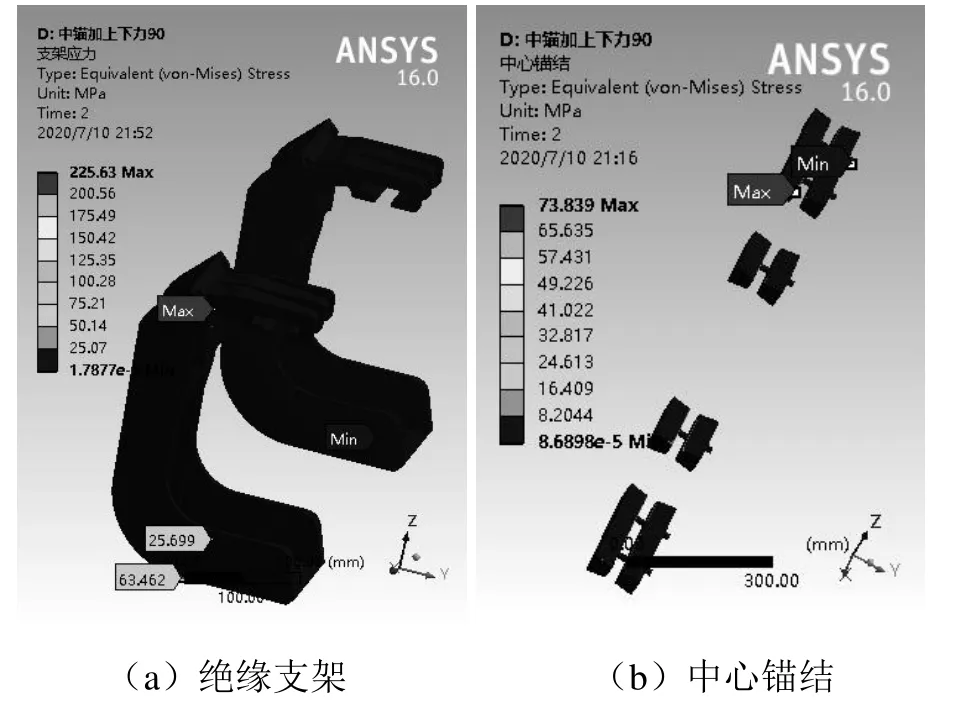
圖7 兩絕緣支架式中心錨結應力狀態

兩絕緣支架式中心錨結結構出現了應力超標情況，中心錨結支架處應力超標，錨結處應力臨界超標（安全系數小于1.5），其中最大應力出現在下支架處右側螺栓孔的位置。可以得出，在250‰坡度下，兩絕緣支架式的中心錨結不足以承受90 m接觸軌的重力載荷。

2.3 兩絕緣支架帶斜拉桿式中心錨結

在標準環境溫度（22℃）下，對兩絕緣支架帶斜拉桿式中心錨結的齒軌鐵路接觸軌系統在承受自重載荷情況下進行靜力學仿真，結果表明中心錨結所在絕緣支架處最大應力為59.839 MPa，中心錨結處最大應力為3.668 MPa，如圖8所示。

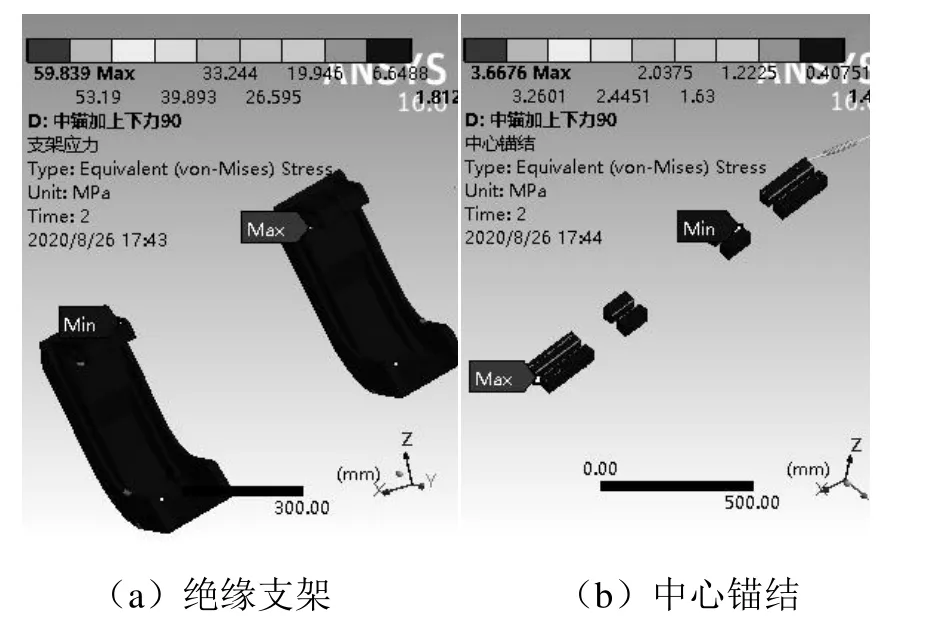
圖8 兩絕緣支架帶拉桿式中心錨結應力狀態

兩絕緣支架帶拉桿式中心錨結結構的應力滿足許用應力要求，這是由于90 m接觸軌的沿線路方向的重力載荷分量被拉桿分擔，中心錨結處及絕緣支架所承受的接觸軌重力載荷相對較小，產生的應力也相應減小。

2.4 對比分析

根據對3種不同中心錨結結構的接觸軌靜力學仿真可知，三絕緣支架式和兩絕緣支架帶斜拉桿式中心錨結應力滿足要求；兩絕緣支架式的中心錨結結構出現了應力超標情況，中心錨結支架處應力超標，錨結處應力臨界超標（安全系數小于1.5）。3種中心錨結形式的零部件應力情況如表3所示。

表3 不同中心錨結結構在5 m跨距、250‰坡度下的零部件應力情況

綜上分析：兩絕緣支架式中心錨結不適合用于250‰坡度下的接觸軌系統，該形式存在多處應力超標的情況；三絕緣支架式和兩絕緣支架帶斜拉桿式結構應力狀態良好，均滿足應力要求。在滿足應力要求及安全運營的前提下，可根據實際情況確定選用何種中心錨結結構。

3 結論

本文根據不同中心錨結結構參數建立了250‰坡度下3種齒軌鐵路接觸軌系統的三維模型，通過靜力學仿真評估了3種中心錨結的結構可靠性，結論如下：

（1）250‰坡度下，兩絕緣支架式中心錨結結構的接觸軌最小安全系數為0.98，出現了應力超標情況。因此，兩絕緣支架式中心錨結結構不適用于大坡度齒軌鐵路接觸軌。

（2）250‰坡度下，三絕緣支架式和兩絕緣支架帶斜拉桿式中心錨結結構滿足90 m接觸軌應力需求，結構的靜力學狀態良好，材料的應力均小于許用應力，最小安全系數為3.75。因此從結構受力方面考慮，三支架式和兩支架帶斜拉桿式中心錨結結構適用于大坡度下齒軌鐵路接觸軌。