受壓T肋被加勁板局部穩定試驗與計算方法

趙秋 陳鵬 林楚 陳友杰

1.福州大學土木工程學院，福州350108；2.福州市建設發展集團有限公司，福州350108

T肋加勁板常應用于鋼箱梁橋的受壓翼緣，斜拉橋與懸索橋的鋼塔以及鋼箱拱橋的鋼拱中。由于大跨度鋼結構橋梁的普及，T肋加勁板須承受更大的軸向壓力，因此受壓穩定問題更加突出［1-3］。

目前，對于T肋被加勁板受壓穩定研究相對較少，多數只研究閉口加勁肋形式下被加勁板的受壓穩定性能。文獻［4］對9塊鋼箱梁U肋加勁板進行軸壓試驗，其中有1塊板件發生被加勁板的局部屈曲破壞，2塊板件發生加勁肋與被加勁板的共同屈曲破壞。文獻［5-6］通過軸壓試驗研究U肋被加勁板的局部失穩破壞，并采用受壓柱理論研究其破壞機理。文獻［7］針對U肋加勁板建立相應的局部穩定試件有限元模型，并通過試驗驗證該數值模擬方法的正確性。上述文獻對閉口U肋加勁下被加勁板的研究較為完善。文獻［8］通過建立數值模型對T肋加勁板在軸壓狀態下的穩定影響參數進行分析，發現T肋加勁板的穩定承載力隨被加勁板幾何初始缺陷半波數量的增加而降低。文獻［9］對T肋加勁板進行建模，提出適用于高強度鋼的加勁板面內抗壓強度計算公式。

橋梁設計中，加勁肋通常設計為剛性加勁肋。被加勁板由于兩端橫隔板以及平面外加勁肋的存在，可視為四邊簡支板［10］。加勁板的局部穩定破壞通常是被加勁板發生局部屈曲，而局部穩定的研究是整體穩定或整體與局部相關穩定研究的基礎。

本文對T肋加勁板中組成板件的被加勁板局部失穩進行試驗研究，并通過有限元分析提出計算方法，為T肋被加勁板的受壓穩定設計提供參考。

1 被加勁板局部穩定試驗

1.1 試件設計

綜合考慮工程常用的尺寸規格、試驗條件以及試驗目的，設計了T肋加勁板試件截面尺寸，長度取被加勁板寬度的3倍［11］，試件橫截面見圖1。改變被加勁板板寬度，試件參數見表1。

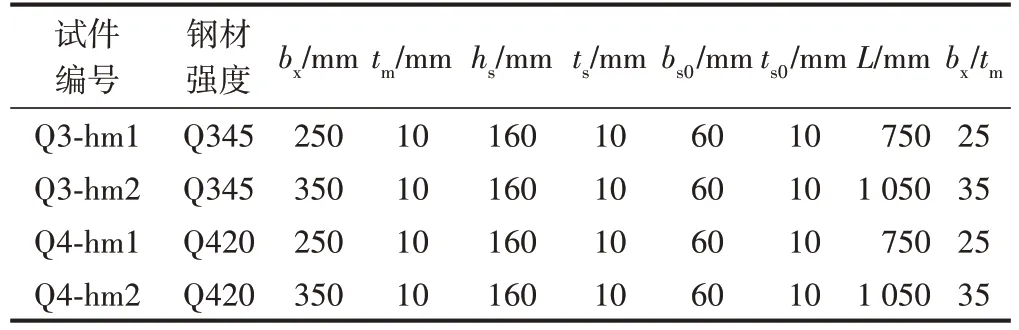
表1 被加勁板局部穩定試件參數

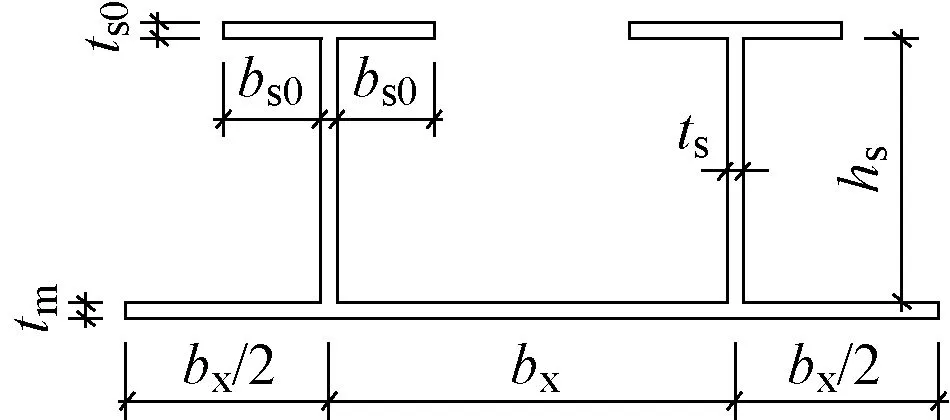
圖1 被加勁板局部穩定試件橫截面

根據GB/T 228.1—2010《金屬材料拉伸試驗第1部分》［12］，制作T肋加勁板局部穩定試驗的標準拉伸試件。在試件中心設應變花，得到Q3、Q4類試件實際屈服強度分別為357，440 MPa，極限強度分別為454，543 MPa，彈性模量均為208 GPa。

1.2 試驗方案

1.2.1 邊界處理

為了正確模擬局部穩定試件在軸壓作用下的試驗邊界，將試件兩端的板件嵌入帶有凹槽的鋼板內，保證試件均勻受壓且不發生滑移，使其處于簡支約束下。開槽鋼板的凹槽略大于試件橫截面尺寸，并在鋼板邊緣位置開孔，保證螺栓可以穿過開孔與承壓端板連接；承壓端板是一塊較厚的平整鋼板，在與開槽鋼板同樣的開孔位置制作螺紋孔；開槽鋼板和承壓端板通過螺栓組成限位裝置，見圖2。

圖2 被加勁板局部穩定試件限位裝置

為保證被加勁板外側懸臂鋼板不會先發生變形，設計采用兩塊角鋼夾住被加勁板的懸臂側鋼板，對懸臂側鋼板的面外剛度進行加勁，同時角鋼不能接觸到端板，不起分攤荷載的作用，見圖3。

圖3 試驗加載

1.2.2 加載方案

試驗加載設備采用最大試驗力為10 000 kN的電液伺服長柱壓力試驗機。正式加載前應先進行預加載。預加載的荷載值為估算極限荷載值的10%～20%。預加載過程中，采用薄鋼片對試件端部的平整度進行調整。預加載完成后卸去全部荷載，讀數歸零后正式加載。正式加載先采用荷載控制，每級加載值為100 kN，加載速率為1 kN/s。當荷載達到預估極限荷載的60%時，繼續向千斤頂油缸送油，改用位移控制，加載速率為0.3 mm/s。在試驗過程中分別采用DH3816靜態應變采集系統定時采集試件的位移，采用試驗機自帶的荷載傳感器采集試件的荷載。

1.2.3 測點布置與量測

被加勁板局部穩定試件上的測點主要包括軸向位移測點和應變測點（圖4）。布置8個量程為100 mm的YHD-100型位移計，測試加勁板在荷載作用下的軸向位移。在加勁板L/4、L/2和3L/4截面處，沿橫向在T肋與被加勁板相連位置和被加勁板中間分別布置應變片和應變花，測試被加勁板在荷載作用下的應變。在固定角鋼的L/2截面處布置應變片，觀測角鋼的受力情況。每一個被加勁板局部穩定試件共需6片BX120-3CA型應變花，8片BX120-1AA型應變片。

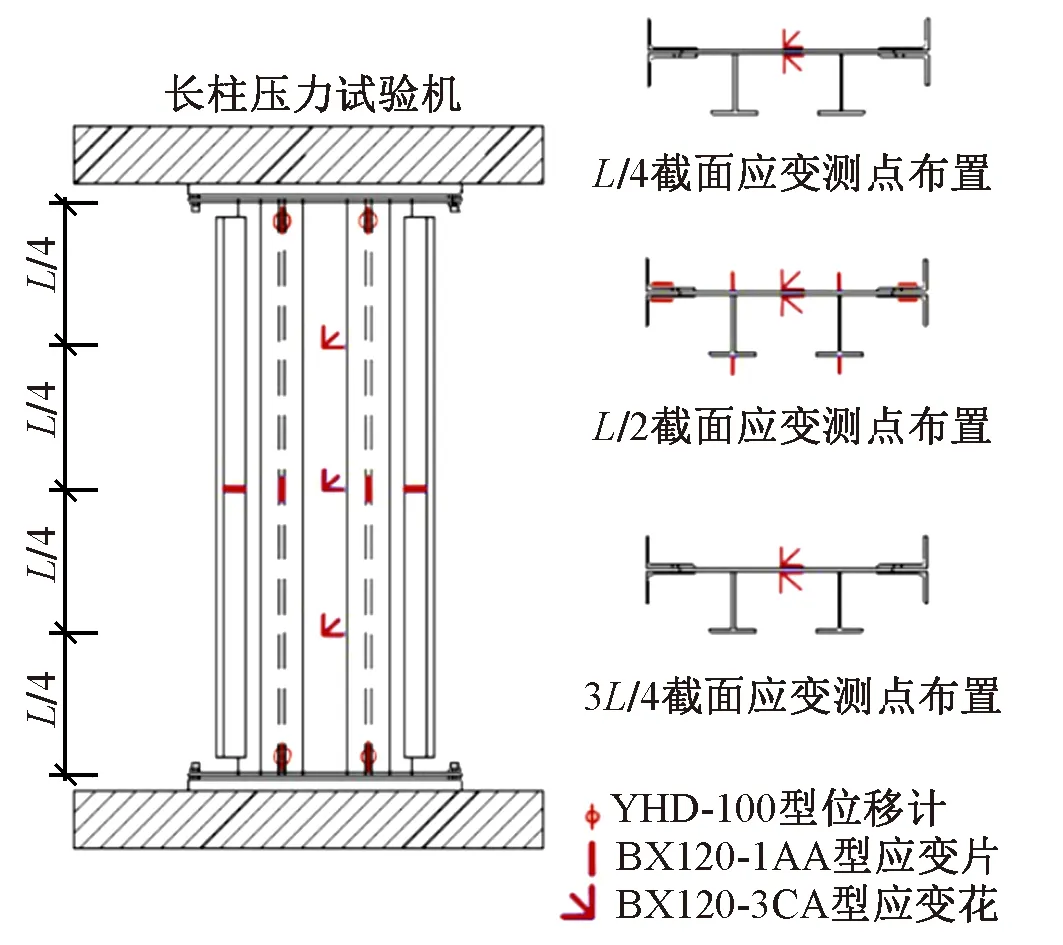
圖4 試件測點布置

1.3 破壞現象分析

對被加勁板局部穩定試件變形部位和方向名稱作統一規定，試件變形方向見圖5。

圖5 試件變形方向

對于Q3-hm1試件，當荷載達到2 749.1 kN（68.4%Nd，Nd為峰值荷載）時，被加勁板L/2處首先產生了向前凸起的微小變形［圖6（a）］；當荷載達到3 249.1 kN（80.9%Nd）時，被加勁板的變形逐漸增大，同時左側翼緣的下端產生向后凹陷的微小變形；當荷載達到峰值荷載4 018.4 kN后下降到3 842.7 kN（95.6%Nd）停止加載。試件最終破壞時，在被加勁板的L/2處有一個向前的波峰，左側翼緣的下端產生向后的微小變形，其他部位沒有明顯變形，見圖6（b）和圖6（c）。

圖6 Q3-hm1試件破壞形態

對于Q3-hm2試件，當荷載達到3 110.4 kN（66.8%Nd）時，被加勁板2L/3處產生向前凸起的微小變形［圖7（a）］；當荷載達到4 117.5 kN（88.4%Nd）時，被加勁板的變形逐漸增大；當荷載達到峰值荷載4 658.6 kN后下降到4 474.7 kN（96.1%Nd）停止加載。試件最終破壞時，被加勁板的2L/3處有一個向前的波峰，被加勁板左右懸臂側的上端（沒有被角鋼固定的位置）均產生了向后的明顯變形，見圖7（b）和圖7（c）。

圖7 Q3-hm2試件破壞形態

對于Q4-hm1試件，當荷載達到3 280.8 kN（72.4%Nd）時，被加勁板2L/3處產生向前凸起的微小變形［圖8（a）］；當荷載達到4 046.7 kN（89.4%Nd）時，被加勁板變形逐漸增大，同時左側翼緣的上端產生向前的微小變形［圖8（b）］；當荷載達到4 528.6 kN時，被加勁板2L/3處的變形更加明顯［圖8（c）］，此時伴隨一聲巨響，左側的固定角鋼頂部接觸到了加載端板，荷載開始短暫上升，達到4 644.7 kN。為了不損壞機器，應停止加載。

圖8 Q4-hm1試件破壞形態

對于Q4-hm2試件，當荷載達到3 604.3 kN（70.1%Nd）時，被加勁板2L/3處產生向前凸起的微小變形［圖9（a）］；當荷載達到4 252.8 kN（82.7%Nd）時，被加勁板的變形逐漸增大；當荷載達到峰值荷載5 142.8 kN后下降到4 995.8 kN（97.1%Nd）停止加載。試件最終破壞時，被加勁板的2L/3處有一個向前的波峰，被加勁板左右懸臂側的上端（沒有被角鋼固定的位置）均產生了向后的明顯變形，見圖9（b）和圖9（c）。

圖9 Q4-hm2試件破壞形態

綜上所述，由于T形加勁肋的作用，4個試件的被加勁板均先于翼緣和腹板產生變形進而導致試件破壞。最早產生變形時的荷載為66.8%Nd～72.4Nd，位于試件L/2處（Q3-hm1試件）或2L/3處（Q3-hm2、Q4-hm1和Q4-hm2試件）。

根據試驗現象將被加勁板局部穩定試件的破壞過程分為3個階段（圖10）：①未發生變形的階段；②被加勁板L/2附近產生向前凸起的微小變形，其他部位沒有產生變形；③被加勁板L/2附近變形明顯，試件達到抗壓承載力峰值。

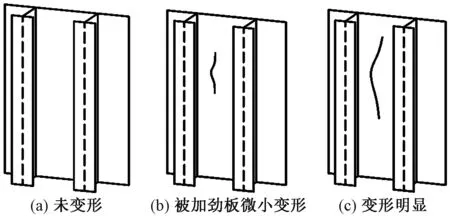
圖10 被加勁板局部穩定試件破壞過程

1.4 試驗結果與分析

為了方便對比不同尺寸的被加勁板局部穩定試件的荷載-位移關系，將試驗荷載和軸向位移分別除以試件實測橫截面積和試件計算長度得到平均應力和平均應變，其關系曲線見圖11。

圖11 試件平均應力-應變曲線

由圖11可知，試件的平均應力-應變曲線經歷了直線段、緩坡段、下降段3個主要階段。直線段試件沒有產生變形，平均應力和應變呈線性增長，應變變化較慢；緩坡段開始時被加勁板開始產生微小變形，隨著荷載增大，變形逐漸增大，平均應變增長較快，斜率逐漸變小，曲線變得平緩，試件出現新的變形時斜率會減小得更快；下降段試件變形不斷增大，曲線斜率為負，平均應力隨著平均應變的增大而減小。

被加勁板試件試驗結果見表2。結合表2和圖11可知：①Q4類試件極限平均應力大于Q3類試件，即相同寬厚比的被加勁板局部穩定試件，材料強度越高，其極限承載能力越大。Q4類試件極限平均應力與屈服強度的比值小于Q3類試件，即相同寬厚比的被加勁板局部穩定試件，材料強度越高，其極限承載能力折減越大。②對于相同材料強度的被加勁板局部穩定試件，寬厚比越大其極限承載能力越小，且寬厚比為35的試件平均應力與極限平均應力的比值均小于寬厚比為25的試件，說明寬厚比越大，試件越早發生屈曲，局部屈曲之后強度的提升空間越大。

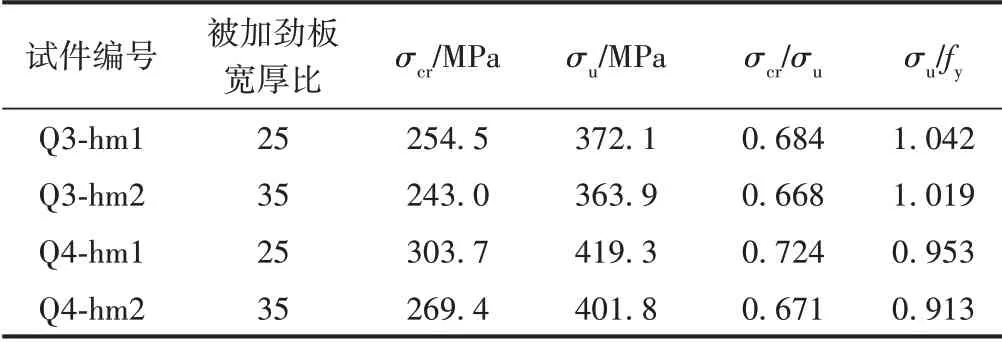
表2 被加勁板試件試驗結果

2 有限元數值模擬方法驗證

采用shell181單元建立有限元模型，采用多線性等向強化模型模擬大應變情況下的應力-應變關系。試驗中限位板較好地約束了試件端部的非軸向位移，因此在有限元中將試件兩端設置為固結支座約束。在試件兩端截面的質心位置分別設置1個mass21單元主節點，然后把試件兩端全部節點的自由度分別耦合到兩端的主節點上。同時約束固定端所有的自由度，約束加載端除軸向位移以外的自由度。以初始應力的形式引入截面殘余應力，殘余應力采用文獻［13］中T肋加勁板殘余應力的實測值；局部初始幾何缺陷采用試件的一階屈曲變形，按固定比例計入，由于試件局部初始幾何缺陷較大，保守取δ/b=1/100（δ為變形值，b為被加勁板寬度）。

2.1 破壞形式驗證

判斷有限元模型是否正確的一個重要指標就是破壞模式是否能與試驗中的破壞模式吻合。不同試件破壞模式與有限元破壞模式對比見圖12。圖中的應力為von Mises應力。

圖12 不同試件破壞模式與有限元破壞模式對比

由圖12可知：①4種試件與有限元模型均發生被加勁板的局部屈曲破壞，且在被加勁板L/2處先發生局部屈曲；②試件大部分位置達到了屈服強度，未達到屈服強度的范圍隨著被加勁板寬厚比的增大而增加，總體吻合情況良好。

2.2 極限承載力與平均應力-應變曲線驗證

試件試驗與有限元計算的平均應力-應變曲線對比見圖13。可知：試驗與有限元的平均應力-應變曲線基本相同，均表現為先直線上升，隨著荷載增加曲線斜率逐漸減小，曲線繼續上升達到峰值平均應力后開始下降，試件處于較好的軸壓狀態，基本沒有發生偏心。Q4-hm1試件因角鋼接觸到加載端板提前結束試驗，導致極限平均應力略小，其他試件極限平均應力有限元計算值均小于試驗值。

圖13 試件試驗與有限元計算的平均應力-應變曲線對比

極限承載力是T肋加勁板軸壓構件最重要的性能指標。試件極限平均應力試驗值與有限元計算值對比見表3。可知，試件極限平均應力試驗值與有限元計算值比較接近，有限元計算值比試驗值平均小0.73%。

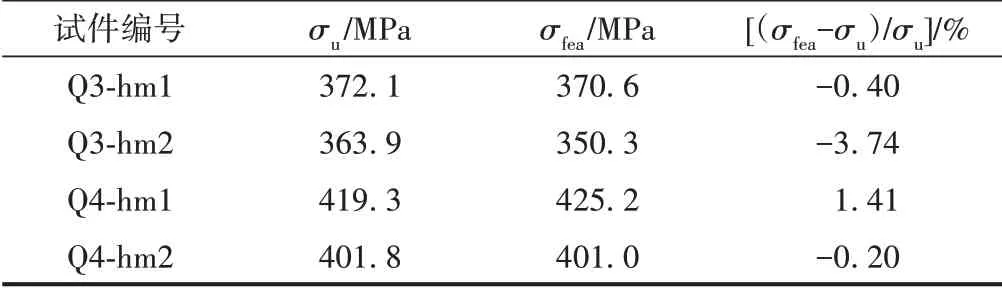
表3 試件極限平均應力試驗值與有限元計算值對比

3 受壓T肋被加勁板局部穩定分析

3.1 計算模型尺寸參數擬定

基于有限元數值分析模型對T肋被加勁板的局部屈曲性能進行參數化分析，研究材料本構模型、簡化焊接殘余應力和局部初始幾何缺陷對局部屈曲性能的影響。模型以一個寬厚比較小的標準尺寸為基準，橫向建立3個相同的T形加勁肋。為防止被加勁板兩側懸臂先發生失穩，采用與第2節相同的方法對被加勁板兩側懸臂進行約束。

被加勁板局部穩定計算模型包含6種模型尺寸，被加勁板的寬厚比范圍取25～50，腹板的寬厚比為16，翼緣的寬厚比為6。模型的長度取被加勁板寬度的3倍。其中M-25和M-35計算模型的尺寸分別為Q3-hm1和Q3-hm2試件的尺寸。被加勁板局部穩定計算模型橫截面與參數分別見圖14和表4。

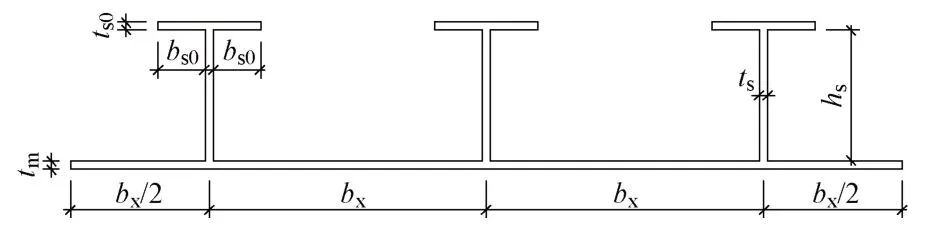
圖14 被加勁板局部穩定計算模型橫截面

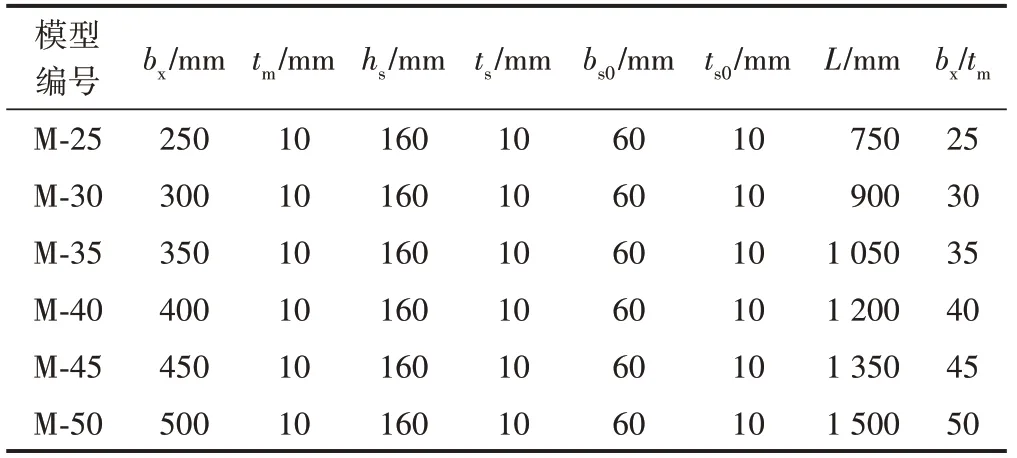
表4 被加勁板局部穩定計算模型參數

3.2 本構模型的影響

本構關系僅考慮鋼材Q345強度的情況。為對比不同本構模型對數值模擬結果的影響，采用四折線本構模型、理想彈塑性本構模型、切線模量為彈性模量1%的兩折線本構模型（簡稱1%切線模型）和切線模量為彈性模量3%的兩折線本構模型（簡稱3%切線模型）分別進行建模計算。4種本構模型見圖15。

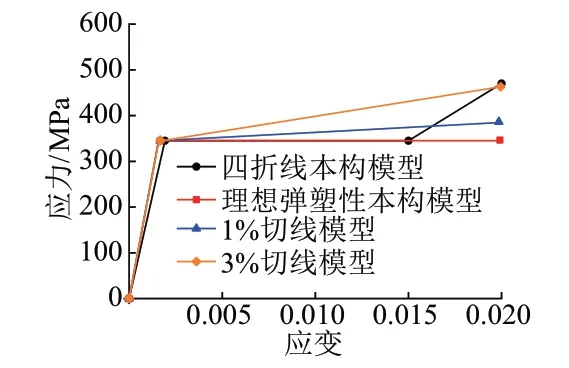
圖15 4種本構模型

有限元模型暫不計入殘余應力的影響，對于局部初始幾何缺陷，取一階屈曲模態下被加勁板寬度的1/200。4種本構模型下穩定系數對比見圖16。可知，被加勁板局部失穩計算模型采用理想彈塑性本構模型的穩定系數與采用四折線本構模型的穩定系數基本相同；采用1%切線模型的穩定系數略大于采用四折線本構模型的穩定系數，二者的差值隨寬厚比的增大而減小；采用3%切線模型的穩定系數明顯大于另外3種本構模型的穩定系數，與四折線本構模型穩定系數的差值隨寬厚比的增大而減小。因此，偏安全地采用理想彈塑性本構模型來計算局部穩定模型的穩定系數。

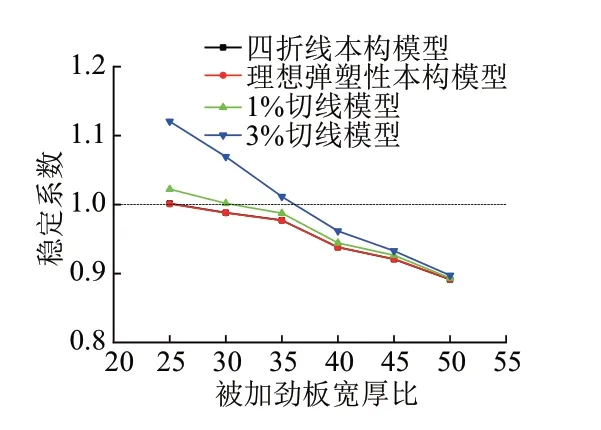
圖16 4種本構模型下穩定系數對比

3.3 焊接殘余應力

3.3.1 簡化殘余應力分布與驗證

計算模型對殘余應力采用以折代曲的簡化方式［13］（圖17）。圖中，lm，c-t為過渡區長度。通過盲孔法對T肋被加勁板的殘余應力進行試驗，并建立對應的有限元模型驗證數值模擬方法的正確性。

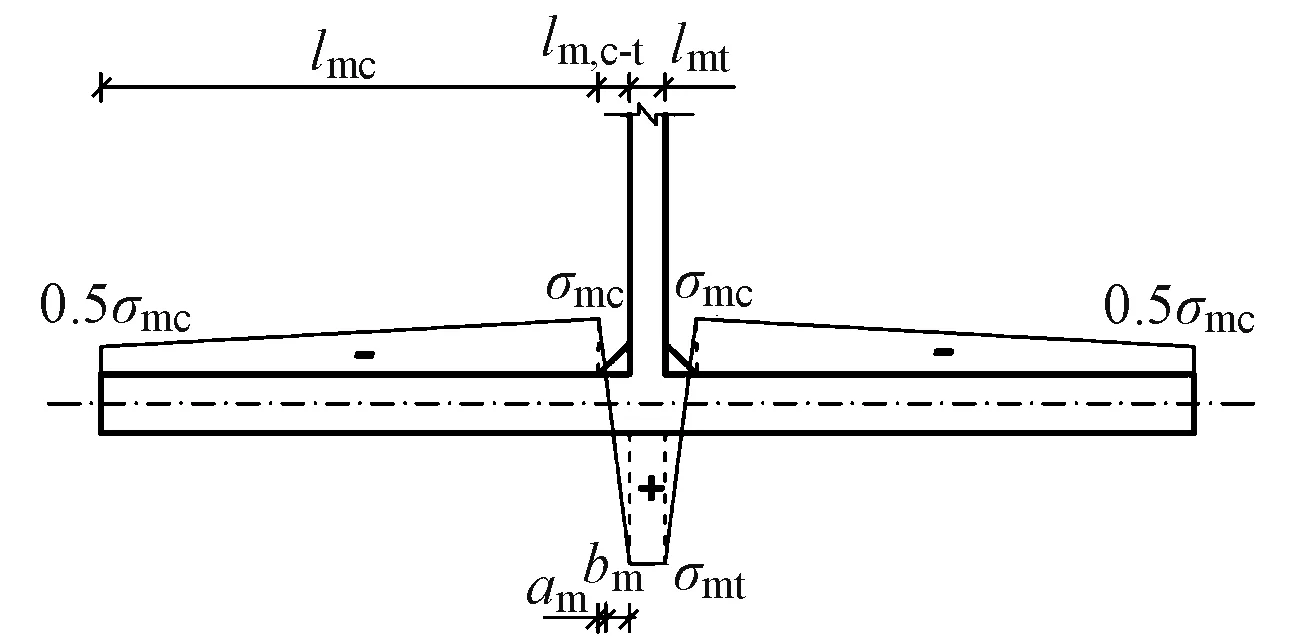
圖17 被加勁板殘余應力簡化分布形式

利用殘余應力的自平衡原理得到T肋被加勁板的殘余應力簡化分布方式，通過式（1）解得殘余應力分布的相關參數am、bm。其中，am與bm通過相似三角形可簡化為一個變量進行求解。

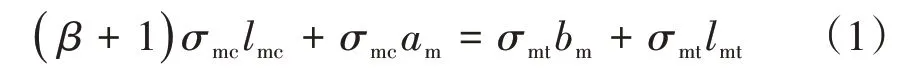
式中：β為殘余壓應力修正系數；σmt為被加勁板殘余拉應力，取被加勁板屈服強度fy；σmc為被加勁板殘余壓應力，取σmc=amfy/bm；am和bm分別為過渡區壓、拉應力長度；lmc和lmt分別為壓、拉應力分布長度。

在被加勁板局部穩定試驗中取Q3-hm1、Q4-hm1試件，在相同局部初始幾何缺陷情況下分析數值模擬和簡化殘余應力分布對試件承載力的影響，見圖18。可知，兩種殘余應力分布方式所得平均應力-應變曲線基本重合。因此，可使用簡化殘余應力分布來分析受壓T肋被加勁板局部穩定性能。

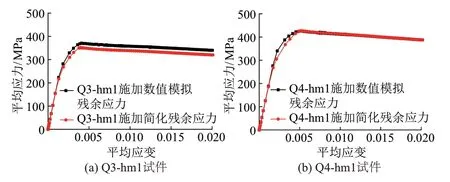
圖18 兩種殘余應力分布對試件承載力的影響曲線

3.3.2 計入簡化殘余應力對穩定系數的影響

對6個不同尺寸的被加勁板計算模型分別計入簡化殘余應力，殘余應力對穩定系數的影響曲線見圖19。可知，計入簡化殘余應力的穩定系數小于不計入殘余應力的穩定系數，且隨寬厚比的增大，穩定系數的減小幅度逐漸增大。

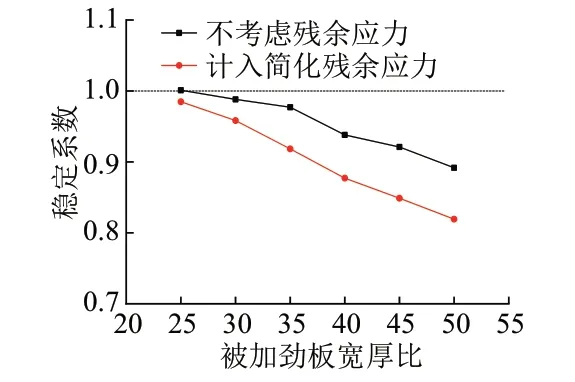
圖19 殘余應力對穩定系數的影響曲線

3.4 局部初始幾何缺陷的影響

為研究局部初始幾何缺陷位置對被加勁板局部穩定性能的影響，采用一致缺陷模態法，取寬厚比最大的M-50模型，計算分別在不同子板件處計入局部初始幾何缺陷后的穩定系數，并繪制應力-應變曲線，見圖20。不同局部初始幾何缺陷位置對應的穩定系數見表5。

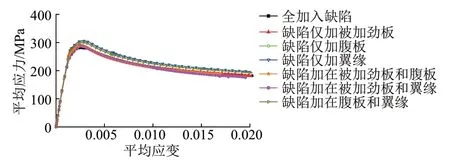
圖20 M-50模型平均應力-應變曲線對比

表5 不同局部初始幾何缺陷位置對應的穩定系數

由圖20和表5可知：①不同局部初始幾何缺陷位置的平均應力-應變曲線總體趨勢相同；②最先發生局部失穩的是被加勁板，當缺陷施加在被加勁板上時，穩定系數比僅施加在腹板、翼緣時更小；③當被加勁板計入局部初始幾何缺陷時，構件軸向剛度減小得快，極限平均應力逐漸減小；④當所有板件均計入局部初始幾何缺陷時，穩定系數最小，對構件的穩定性能最不利。因此，下文均采用構件的子板件全部計入局部初始幾何缺陷來計算模型的穩定系數。

分別計入4種局部初始幾何缺陷幅值（B/50，B/100，B/200，B/300，B為各個被加勁板最大板寬），研究其對被加勁板局部穩定性能的影響，見圖21。可知，局部初始幾何缺陷幅值為B/50的穩定系數最小；被加勁板寬厚比為35時，穩定系數變化幅度最大；穩定系數的變化幅度隨寬厚比的增大而先增大后減小。寬厚比較大時，增大局部初始幾何缺陷的幅值對穩定系數影響較小，原因是極限承載能力在寬厚比較大時已經由于子板件局部失穩而顯著削弱。

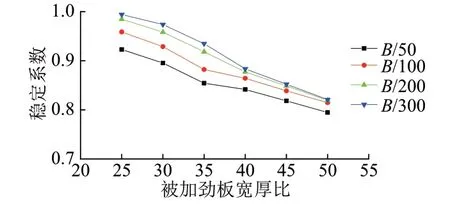
圖21 不同初始幾何缺陷幅值對穩定系數的影響曲線

4 被加勁板局部穩定系數計算方法

4.1 被加勁板局部穩定系數簡化計算公式

為了解被加勁板的屈曲性能和屈曲后強度利用情況，采用改變被加勁板寬度和厚度的方式得到僅被加勁板發生局部失穩時的受壓局部穩定系數。被加勁板寬度為300～700 mm，厚度為10～28 mm；T肋腹板的高度和寬度分別取250，10 mm；T肋翼緣的寬度和厚度分別取80，10 mm。鋼材強度選取常用的Q345和Q420。兩種鋼材強度的模型各有42個，通過建立有限元模型計算板件的相對寬厚比和局部穩定系數，模型采用理想彈塑性本構模型，邊界條件、殘余應力的計入與本文第3節中的方法相同，局部初始幾何缺陷按最大被加勁板寬度的1/200計入。

對被加勁板局部穩定模型的計算結果分別采用多項式和Perry公式進行擬合。多項式擬合曲線的計算公式見式（2）和式（3）。

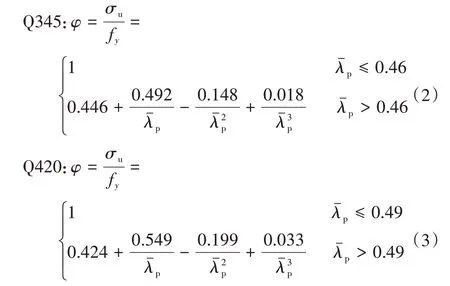
Perry公式擬合曲線的計算公式見式（4）和式（5）。

被加勁板局部穩定擬合曲線對比見圖22。

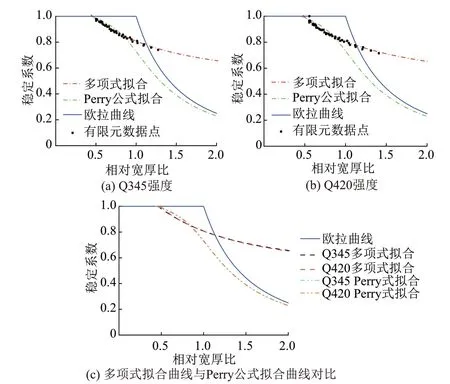
圖22 被加勁板局部穩定擬合曲線對比

由圖22（a）和圖22（b）可知：①Q345強度的多項式擬合曲線穩定系數開始發生折減的相對寬厚比為0.46，略小于Q420強度開始折減的相對寬厚比0.49。多項式擬合曲線與有限元數據點整體吻合較好，在相對寬厚比達到1.14后大于歐拉曲線，說明被加勁板開始利用屈曲后強度。②Q345強度的Perry公式擬合曲線穩定系數開始發生折減的相對寬厚比為0.44，略小于Q420強度開始折減的相對寬厚比0.45，且不考慮屈曲后強度。③不同強度的Perry公式擬合曲線在相對寬厚比小于0.93時與有限元數據點吻合良好，當相對寬厚比大于0.93時Perry公式擬合曲線下降較快，直至相對寬厚比為2.0時也未大于歐拉曲線。

由圖22（c）可知：不同鋼材強度的多項式和Perry公式擬合曲線整體變化趨勢基本相同，說明不同鋼材強度對穩定系數的影響較小；Perry公式擬合曲線比多項式擬合曲線更早開始折減。在相對寬厚比小于0.84時，Perry公式擬合曲線得到的穩定系數大于多項式擬合曲線得到的穩定系數，當相對寬厚比大于0.84時規律相反；多項式擬合曲線在相對寬厚比大于1.14后大于歐拉曲線。因此，相比于多項式擬合曲線，Perry公式擬合曲線不考慮屈曲后強度更加安全。

4.2 被加勁板穩定系數折減曲線對比

將被加勁板局部穩定系數簡化公式與JTG D64—2015《公路鋼結構橋梁設計規范》［14］（簡稱中國規范）、日本道路橋示方書［15］、美國規范AASHTO［16］和歐洲規范EUROCODE［17］相關規定曲線進行對比，見圖23。

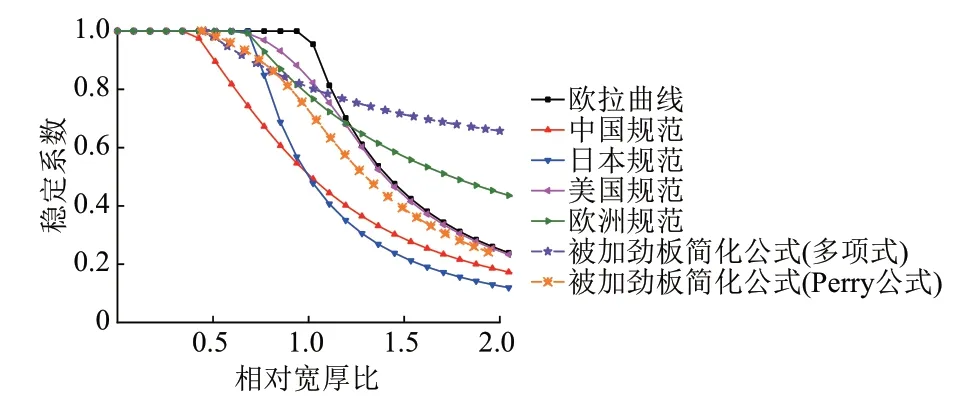
圖23 局部穩定系數折減曲線與各國規范曲線對比

由圖23可知：

1）中國規范、日本規范和美國規范的局部穩定系數折減曲線均在歐拉曲線的下方，表明這些規范不允許加勁肋之間的板件發生局部屈曲。

2）中國規范曲線開始折減的寬厚比小于日本規范曲線開始折減的相對寬厚比，在相對寬厚比小于1.0時，中國規范曲線折減較快，且位于日本規范曲線下方；當相對寬厚比大于1.0時，日本規范曲線折減極快，中國規范曲線位于日本規范曲線的上方。說明中國規范在相對寬厚比較小時比較保守，日本規范不推薦使用相對寬厚比較大的構件。

3）歐洲規范曲線開始折減的相對寬厚比較大，在相對寬厚比大于1.2時穩定系數大于歐拉曲線，說明歐洲規范允許加勁肋之間的板件發生局部屈曲，當相對寬厚比較大時可以利用構件的屈曲后強度。

4）多項式擬合曲線在相對寬厚比較大時也利用了屈曲后強度，因此將其與歐洲規范曲線進行對比。可以看出，多項式擬合曲線開始折減時的相對寬厚比小于歐洲規范開始折減的相對寬厚比。隨著相對寬厚比增加，多項式擬合曲線折減較慢，逐漸高于歐洲規范曲線。

5）Perry公式擬合曲線沒有考慮利用屈曲后強度，因此將其分別與中國規范、美國規范和日本規范曲線進行比較。Perry公式擬合曲線開始發生折減的相對寬厚比大于中國規范曲線開始折減的相對寬厚比，小于美國規范和日本規范曲線開始折減的相對寬厚比。Perry公式擬合曲線整體介于中國規范曲線與美國規范曲線之間，與美國規范曲線更接近。因此，可以偏安全地采用Perry公式擬合曲線進行計算。

5 結論

1）T肋被加勁板局部穩定試驗中所有試件均發生了被加勁板的局部失穩，被加勁板寬厚比越大，試件越早出現局部屈曲變形，極限承載能力折減越大，局部屈曲之后強度的提升空間越大。

2）有限元計算模型采用理想彈塑性本構模型模擬，并計入已驗證的簡化殘余應力，子板件全部計入局部初始幾何缺陷，其中局部初始幾何缺陷取板寬的1/200。有限元計算值與試驗值吻合情況良好。

3）被加勁板相對寬厚比越大，穩定系數折減得越多，穩定系數折減的幅度在計入局部初始幾何缺陷時呈現先增大后減小的趨勢，且當局部初始幾何缺陷施加在最先發生局部失穩的子板件上時，穩定系數折減得較明顯。

4）鋼材強度對被加勁板局部穩定系數影響較小，隨著相對寬厚比增加，多項式擬合曲線逐漸高于歐洲規范曲線，考慮板件屈曲后強度；而采用Perry公式擬合曲線整體均位于歐拉曲線的下方，介于中國規范曲線與美國規范曲線之間，不考慮板件屈曲后強度。因此，可以偏安全地采用Perry公式擬合曲線進行計算。