基于點安全系數法的邊坡穩定性評價研究

譚清順

(齊齊哈爾市鐵鋒區水利站，黑龍江 齊齊哈爾 161000)

0 引 言

當邊坡滑面單元全部屈服，邊坡安全系數也能大于1，邊坡處于安全穩定狀態[1]。邊坡失穩時，需所有滑面單元垂直正應力和平行剪應力同時達到屈服條件。滑面單元點的抗剪強度表達式為：

τu=c+σntanφ

(1)

式中：τu為平行剪應力；σn為垂直正應力；φ為內摩擦角；c為黏聚力。

點安全系數法評估滑坡的穩定性基于所求的滑坡安全系數。首先確定滑面具體位置，計算得出滑面單元的應力應變狀態，分析其變化規律，進而求解滑面單元的點安全系數，據規范標準可分析單元破壞及整體邊坡滑面的穩定性。

1 有限元原理及評價機理

1.1 Druker-Prager彈塑性本構模型

該模型主要為應用巖石材料的理想彈塑性模型，應力-應變關系如圖1所示[2]。

圖1 理想彈塑性模型應力應變關系示意圖

D-P屈服準則的表達式為：

(2)

I1=σ1+σ2+σ3

(3)

J2=[(σ1-σ2)2+(σ1-σ3)2+(σ2-σ3)2]/6

(4)

式中：I1為應力第一不變量；J2為偏應力第二不變量；a，κ為材料常數。

各準則參數變換滿足的關系見表1，π平面的D-P屈服準則關系如圖2所示[3]。

表1 D-P各準則參數變換表

圖2 π平面的屈服準則關系曲線

1.2 評判準則

屈服準則可評判處巖體任一單元點的安全狀態，準則關系如下[4]：

(5)

點安全系數的評判關系見下式。

(6)

2 工程實例

2.1 工程概況

某高邊坡位于汶水河與白龍江交會的左岸處，水電站在河流交叉處下游4km，樞紐壩坡坡體面積約2km2，呈一“V字型”地貌。邊坡體力學參數的取值范圍見表2[5]。

表2 邊坡體力學參數取值范圍表

2.2 有限元模型

為實際反應該邊坡結構的應力狀態，計算區域選取邊坡Ⅰ區建立有限元模型，三維坐標系采用Ⅰ區6個測點的反分析特征點模型。模型共劃分為單元54367個、結點13674個。邊坡有限元模型及單元劃分如圖3所示。

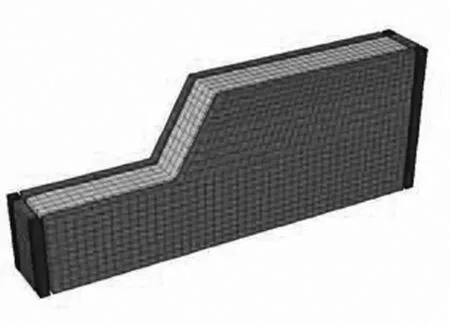
圖3 邊坡有限元模型網格圖

2.3 邊坡穩定性步驟

1)利用ANSYS有限元計算單元體應力應變。

2)通過ANSYS后處理程序的ETABLE命令，在單元列表中輸入S1、S2、S3三個主應力計算結果。

3)在CALC模塊中進行算術運算。

4)使用PRETABB命令查看計算運行結果并輸出FS等值線圖。

2.4 有限元分析

為客觀進行BP神經網絡和GA-BP網絡反分析結果對比分析，從30組實驗中選取5組(第3、8、13、18、23組)樣本用于測試檢測網絡的性能，其余25組用于訓練神經網絡，以終止進化代數做為程序終止條件，6個測點通過訓練得到結果見圖4和圖5。

圖4 BP與GA-BP網絡測試結果圖(E3值)

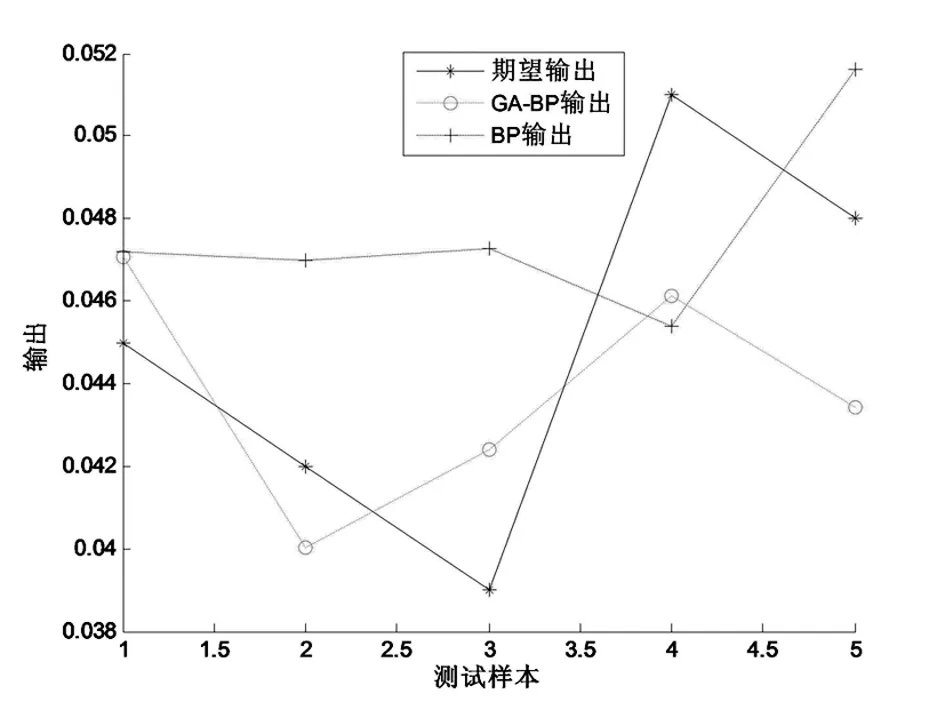
圖5 BP與GA-BP網絡測試結果圖(C3值)

由圖可知，BP網絡E3值、C3值相對誤差最大值分別為為-13.35%和-21.17%，最小值為1.41%和4.84%，計算值和期望值的相對誤差大部分保持在8.5，說明二者的網絡模型預測精度均較高，但GA-BP模型相對誤差在6%內的數據明顯較多，說明GA-BP模型預測精度更高。

不同模型的預測平均相對誤差值比較見表3。

表3 模型樣本平均誤差比較表

圖6為邊坡點安全系數FS等值線計算云圖。

圖6 點安全系數Fs等值線云圖

根據《巖土工程勘察規范》(GB50021—2001)，邊坡穩定最小安全系數取值范圍為1.10-1.25，由上圖可知，該邊坡求得最小點安全系數是1.46，表明該邊坡整體安全穩定，同時具備一定的安全儲備。

3 結 論

文章基于點安全系數的理論、特點和Druker-Prager彈塑性本構模型基本原理，建立某邊坡的三維有限元模型，計算應力應變分布，同時根據不同網絡模型對比穩定性評價適宜性，最終得出該邊坡的各點安全系數，通過最小點安全系數1.46認為整體邊坡是安全穩定性的，兼具一定的安全儲備。