離散波長消色差超構透鏡的性能分析

肖行健，祝世寧，李 濤

（南京大學現代工程與應用科學學院，江蘇南京， 210023）

1 引 言

超構透鏡是由一系列亞波長尺寸的單元結構組成的新型衍射透鏡，與傳統的折射透鏡相比，其厚度只有光波長量級，具有輕薄的優勢[1-2]；而與傳統的衍射透鏡相比，由于它由亞波長尺寸單元結構組成，能有效抑制高階衍射，因此具有更高效的調控效率[3-4]。不過，超構透鏡繼承了傳統衍射透鏡的色散特性，具有較大的色差，而色差的存在會嚴重影響透鏡在非單色光照明下的成像性能。雖然近年來人們已經發展出一些設計方案用以實現在連續波長范圍內消色差的超構透鏡（簡稱為寬譜消色差超構透鏡）[5-10]，但是這些方案設計的透鏡存在尺寸較小、數值孔徑較低或工作帶寬過窄的問題。實際上這是由于這些參數之間存在一定的制約關系所致[7,11]。因此，如何設計大尺寸、高數值孔徑并且工作帶寬較寬的超構透鏡仍然是一個挑戰。幸運的是，在很多白光成像的實際應用場景中，光電探測器往往并不直接接收整個連續光譜的光場，而是采用濾波器陣列將光場過濾為紅綠藍三色（RGB），然后利用三種單色探測器單元進行接收[12]。此時僅針對幾個離散波長進行透鏡的消色差設計就能夠滿足成像系統的要求，同時也可以克服連續波段消色差在器件尺寸和工作效率上的局限。近年來人們提出了一些離散消色差超構透鏡的設計方案[13-16]。結果顯示，離散消色差超構透鏡確實可以突破寬帶消色差透鏡制約關系的限制，同時實現較大尺寸、較高數值孔徑及更高的工作效率。

不過，對于離散消色差超構透鏡，仍有兩個問題值得討論。一是在尺寸和數值孔徑均相同的情況下，離散消色差超構透鏡相對于寬帶消色差超構透鏡在設計原理上有什么差異，能否在指定工作頻率下獲得更高的效率？二是離散消色差超構透鏡孤立工作頻率之間的間隔對所設計的透鏡的效率是否存在影響？理解這兩個問題對于具體實際應用中透鏡參數的選擇具有重要的指導作用。本文將通過理論分析和模擬計算的方式，討論相同參數下離散消色差超構透鏡和寬譜消色差超構透鏡在效率上的差異，并考察離散消色差超構透鏡的聚焦效率與對應頻率間隔大小之間的關系。

2 離散與寬帶消色差超構透鏡差異分析

2.1 理論分析

一般而言，為了使入射光場會聚到焦點處，超構透鏡提供的波前相位調制需要滿足雙曲相位[17]：

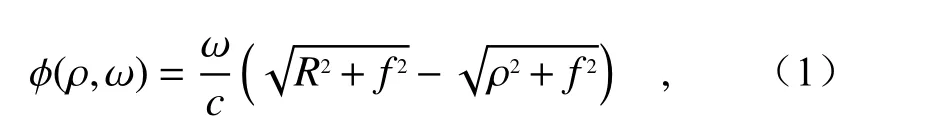
式中ω為角頻率，c為真空中光速，R為透鏡半徑，f為焦距，ρ為徑向坐標。對于消色差超構透鏡，需要波前相位在多個頻率或整個頻率范圍內都滿足式(1)。實際提供調制相位的是一系列不同尺寸不同形狀的亞波長結構單元。單個結構提供的相位可以表示為[18]：

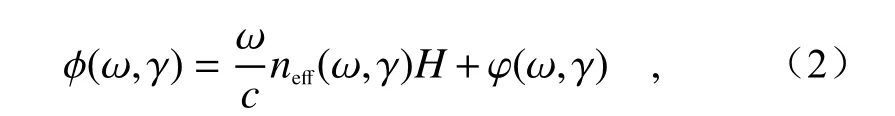
式中H為結構高度，neff為有效折射率，γ為結構形狀參數。式(2)等號右邊的第一部分為導波模式帶來的傳播相位，第二部分為傳播相位以外的突變相位，主要包括共振相位和幾何相位。一般來說突變相位的調控范圍不大，其值通常在0到2π 之間。

現在考察離散消色差與寬帶消色差超構透鏡的設計差異。為了方便分析，引入相位色散空間的概念：假設所考察的消色差頻譜范圍為[ω1,ω2]，設最低頻率ω1對應的相位為Φ，最高頻率ω2與最低頻率ω1對應相位的差值為ΔΦ，則可以定義一個以Φ和ΔΦ作為橫縱軸組成的空間，這里將其稱為相位色散空間。圖1(a)為關于兩個頻率的相位分布示意圖，圖1(b)為其對應的相位色散空間。離散消色差超構透鏡和寬帶消色差超構透鏡設計上的差異主要體現在對于相位差ΔΦ的處理上。對于離散消色差超構透鏡（以兩個頻率為例），由于相位只需要在兩個頻率處滿足式(1)，因此可以通過取模2π 的方式將所需相位差ΔΦn約化到[0, 2π]。以圖1(c)左圖為例（以Multiwavelength表示離散消色差超構透鏡結果），紅色虛線為[ω1,ω2]區間內原本的色散關系，ω2對應的相位由紅點表示，若將ω2處的相位減少2π，則ω2轉移到藍點位置，此時色散關系變為藍色虛線。兩種色散對于離散頻率ω1和ω2等價，因此，單元結構提供藍色虛線對應的相位色散便可以滿足兩個頻率處所需相位。對于寬帶消色差超構透鏡，如圖1(c)右圖所示（以Broadband 表示離散消色差超構透鏡結果），所需的相位色散由紅色直線表示，此時結構在任一頻率處提供的相位都要在這一直線上。若ω2處所需相位減少2π，使相位色散變為藍色直線，雖然此時在ω1與ω2處的相位均滿足理論需求，但是處于這兩個頻率之間的其它頻率（設為ω3）對應的相位卻不滿足理論需求，因為其變化的相位小于2π，而不為2π 的整數倍，如圖中綠色箭頭所示。因此，在寬帶消色差超構透鏡的設計中，無法通過取模2π 的方式將所需的相位差ΔΦ約化到[0,2π]。圖1(d)為將圖1(b)中相位和相位差均約化后得到的分布，對于離散消色差超構透鏡，橫縱坐標均可以取模2π，所需要結構提供的最大相位差maxΔΦ為2π，而對于寬帶消色差超構透鏡，只能對橫坐標取模2π，所需要結構提供的最大相位差maxΔΦ約為28π。由于共振相位一般只能提供2π 以內的相位，對于大于2π 的相位差需要由傳播相位提供。根據式(2)，傳播相位大小主要由結構高度決定，在結構高度為波長量級的情況下，傳播相位只能提供一到兩倍2π 的相位差，可以滿足離散消色差超構透鏡所要求的相位差，但無法滿足寬帶消色差透鏡所要求的遠大于2π 的相位差，因此基于該尺寸的結構所設計的寬帶消色差透鏡調制波前與理論值會有較大的誤差。基于以上分析，可以預測在透鏡尺寸與數值孔徑較大、而厚度維持在波長量級的情況下，設計得到的離散消色差超構透鏡在設計波長處的平均效率會顯著高于寬帶消色差超構透鏡在整個消色差帶寬內的平均效率。

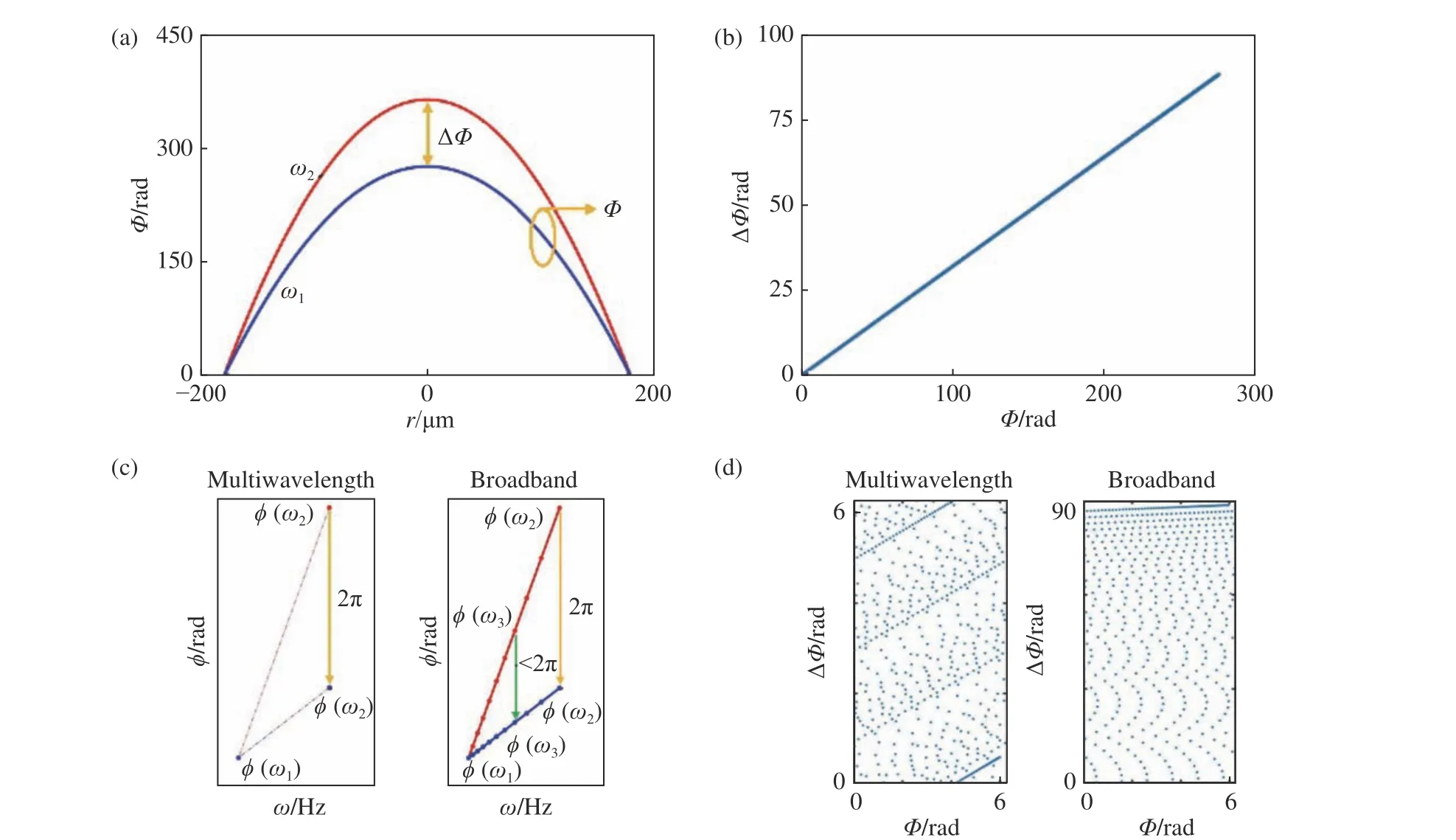
圖1 理論分析示意圖。（a）兩個頻率ω1與ω2的相位分布示意圖；（b）相位色散空間示意圖；（c）離散消色差與寬帶消色差超構透鏡相位處理上的差異；（d）約化后的相位色散空間。Fig.1 Diagram for analyzation.(a)The phase distribution at frequency ω1and ω2;(b) phase-dispersion space;(c)difference in multiwavelength metalens and broadband metalens when it comes to phase processing;(d)phase-dispersion space after mod 2π.

2.2 計算驗證

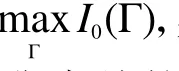
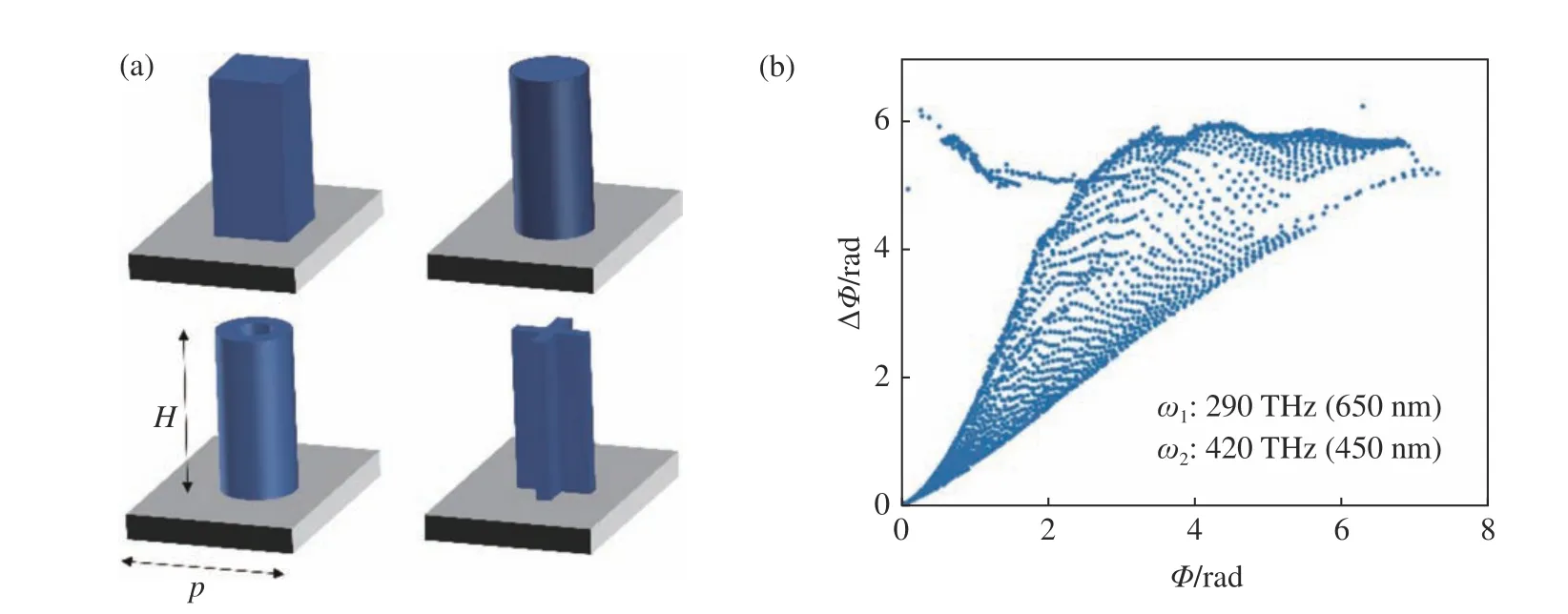
圖2 單元結構示意圖及色散分布。（a）單元結構示意圖。高度H=1μm，周期p=350 nm；（b）結構提供的相位色散分布圖。Fig.2 Schematic of meta-unit and it’s phase-dispersion distribution.(a)Schematic of meta-unit.Height H=1μm, periodic p=350 nm;(b) phase-dispersion provided by themeta-unit

基于上述提到的方法，首先設計了一個離散雙波長消色差超構透鏡（設計波長分別為450 nm、650 nm）和一個準寬帶消色差超構透鏡（設計波長在450～650 nm 中取21個波長，間隔為10 nm）。利用標量衍射理論，計算了沿傳播方向的衍射場，如圖3(a)、3(b)所示。可以看到，所設計波長對應的光場均聚焦在指定的焦距處。定義聚焦效率為焦面上焦斑三倍半高寬內的能量與透鏡出瞳處的能量比值[7,11]，不同波長下的聚焦效率，如圖3(c)所示。可以看到，對于離散消色差超構透鏡，所設計頻率處的平均聚焦效率大概在75%左右，而對于寬帶消色差超構透鏡，平均聚焦效率大概為18%。上述結果證明了之前分析得出的結論。其次，設計了針對不同頻率數的離散消色差超構透鏡。在保持波段為450～650 nm不變的前提下，設計了針對1個頻率聚焦、2個頻率消色差、3個頻率消色差…21個頻率消色差的超構透鏡，并按照之前的方案計算其設計頻率處的平均聚焦效率。圖3(d)為平均聚焦效率關于設計波長數目的分布，可以看到，隨著優化波長數目的逐漸增加，平均聚焦效率從80%逐步下降到18%。同時，在波長數大于11后，效率變化極小，基本處于20%左右，此時可以認為所設計的透鏡類似于一個寬帶消色差超構透鏡。綜上所述，在設計尺寸和數值孔徑較大的情況下，離散消色差超構透鏡的平均聚焦效率會顯著高于寬帶消色差超構透鏡。隨著設計頻率數目的增加，平均聚焦效率下降，最終會與寬帶消色差超構透鏡效率一致。不過，對于離散波長消色差超構透鏡而言，其參量之間是否也存在一定的制約關系？實際上，與寬帶消色差超構透鏡相比，離散波長消色差超構透鏡的參量僅有一項有所改變，即消色差頻譜寬度Δω變為了離散波長對應的間隔δω，接下來將討論雙波長離散波長消色差超構透鏡的聚焦效率與δω之間的關系。

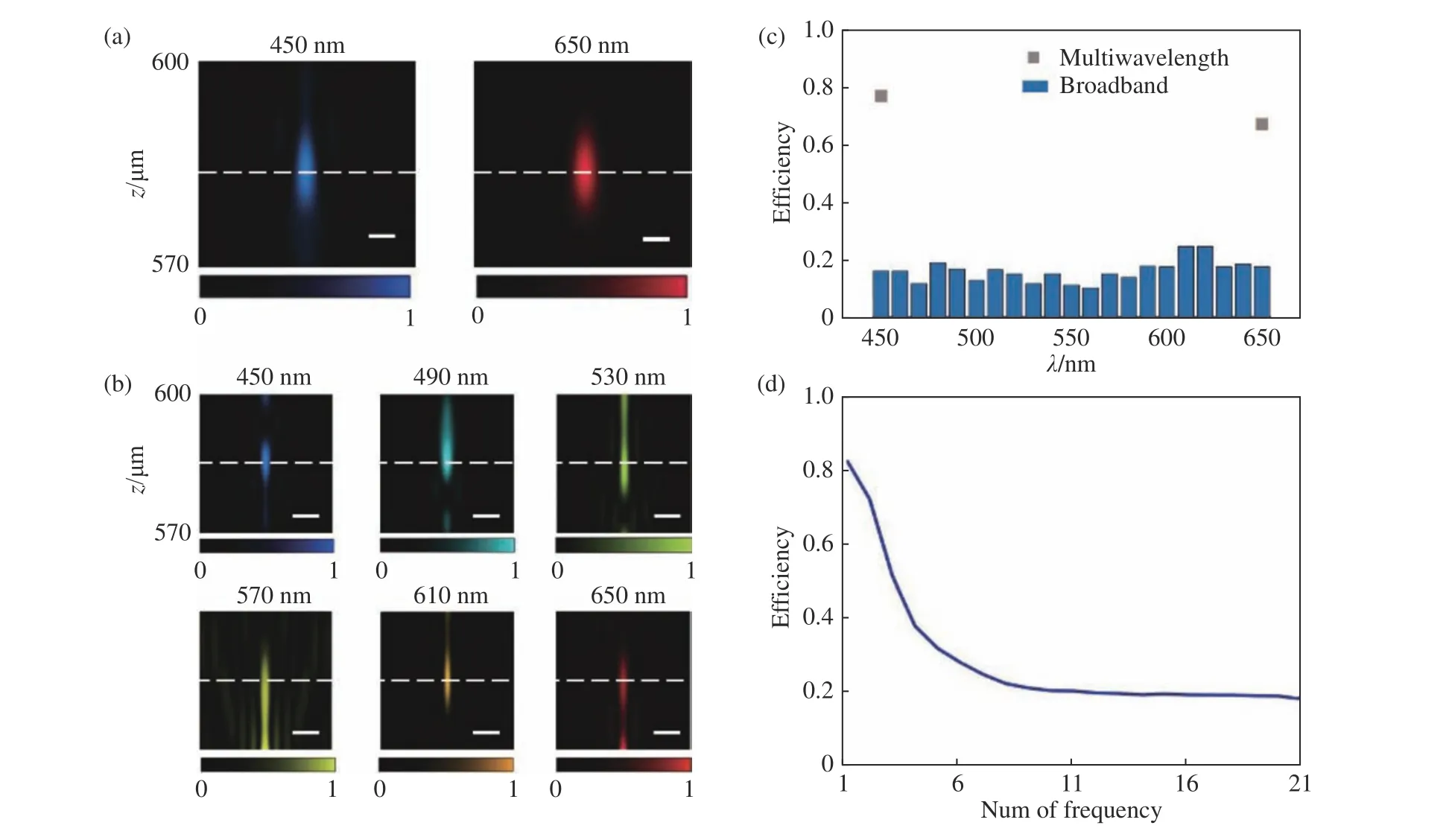
圖3 設計樣品對應的光場分布及聚焦效率。（a）離散消色差超構透鏡在設計波長處軸向光場分布。比例尺為500 nm；（b）寬帶消色差超構透鏡在6個波長處軸向光場分布。比例尺為1μm；（c）離散消色差超構透鏡和寬帶消色差超構透鏡在設計波長處的聚焦效率；（d）離散消色差超構透鏡在平均聚焦效率隨設計波長數目的變化Fig.3 The light fields and focus efficiencies of the designed samples.(a)Light field of multiwavelength metalens at thewavelengths 450 nm and 650 nm along the propagation axis.Scale bar,500 nm;(b)light field of broadband achromatic metalens at six wavelengths along the propagation axis.Scale bar,1μm;(c)the focus efficiency of multiwavelength metalens and broadband achromatic metalens at the designed wavelengths;(d)the distribution of focus efficiency with respect to thenumber of designed wavelength

3 離散波段消色差效率與消色差頻率間隔的關系

3.1 理論分析

對于雙波長消色差超構透鏡，效率關于頻率間隔的分布可以分為兩個區間進行討論。第一個區間為頻率間隔較小的區間。基于波動光學理論，聚焦光場沿軸向有一定的焦深（Depth Of Focus,DOF）[1]：

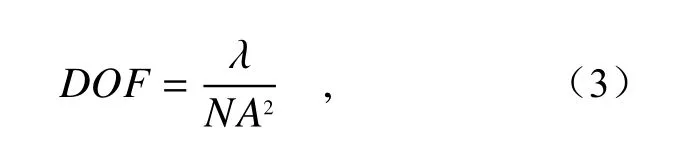
其中，λ為光場的波長，NA為透鏡的數值孔徑。若兩頻率間隔極小，滿足其焦距差值小于其中一個頻率光場對應的焦深，即：

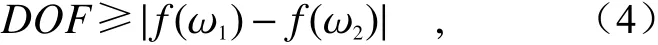
此時可以認為，即便是針對單一頻率ω1設計的超構透鏡，對另外一個頻率ω2也基本不存在色差，此時超構透鏡對兩種頻率光場的平均聚焦效率均會接近理想狀態。隨著頻率間隔的增大，焦距差值逐漸增大，最終使得式(4)不再成立，相應的聚焦效率也會下降。因此在這個區間內，效率隨頻率間隔呈下降趨勢。第二個區間為頻率間隔較大的區間，此時的分析將基于之前提出的相位色散空間。本文把通過電磁仿真得到的單元結構實際提供的相位和相位差記為(Φr,ΔΦr)，實現消色差功能理論所需的相位和相位差記為(Φn,ΔΦn)。如前所述，對于離散消色差超構透鏡，相位色散空間總可以將表示成一個[0,2π]×[0,2π]的空間。利用這個空間，可以直觀地表示出單元結構所能提供的相位色散分布(Φr,ΔΦr)以及實現消色差超構透鏡所需要的相位色散分布(Φn,ΔΦn)。圖4(a)給出了幾組不同頻率下，單元結構所能提供的相位色散分布(Φr,ΔΦr)。可以看到，在頻率間隔較小的情況下，相位色散分布占整個相位色散空間的比例較小，而在頻率間隔較大的情況下，對應分布占比較大。這是因為對于高度為波長量級的結構(如1μm 高度的SiNx 結構)，在非共振峰附近，其提供的相位關于頻率接近線性分布(主要由傳播相位提供，對應式(2)的第一項)[6]。因此，在頻率間隔較小的情況下，單元結構所能提供的相位差值ΔΦr較小，隨著頻率間隔的增大，結構所能提供的相位差值ΔΦr也隨之增大。圖4(b)給出了對應頻率實現消色差超構透鏡所需要的相位色散分布(Φn,ΔΦn)，該分布由式(1)計算得到(其中R=180μm，NA=0.3)。從圖中可以看出，即便在頻率間隔較小的情況下，所需的相位色散分布在整個空間中的占比也較大，而隨著頻率間隔增大，所需分布覆蓋了整個[0,2π]×[0,2π]空間。這是因為根據式(1)，隨著透鏡尺寸增大，兩頻率下的相位差值也會增大，使得對于一個尺寸相對較大的超構透鏡，即便兩頻率間隔較小，所需提供的相位差值也會較大。通過對比(Φr, ΔΦr) 和(Φn, ΔΦn)，可以發現在頻率間隔較小時，兩者重合程度較低，也即最終設計得到的相位分布相對于理想情況偏離較大，而隨著頻率間隔增大，兩者重合程度增大，偏離會逐漸減小。因此可以預測，在這個區間內，效率隨頻率間隔呈上升趨勢。

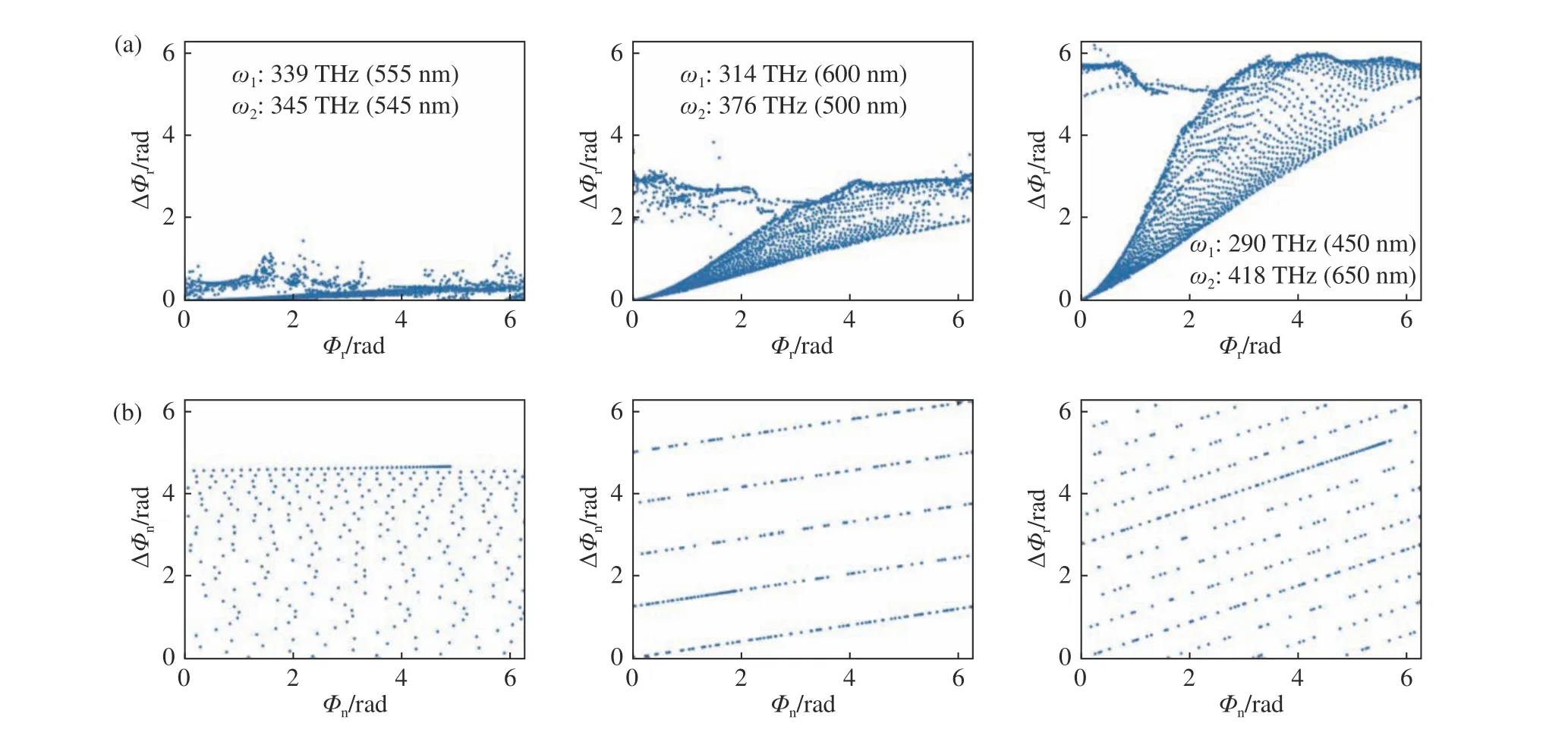
圖4 結構提供的色散分布和實際所需色散分布。（a）不同頻率下結構所能提供的相位色散分布;（b）不同頻率下實現離散消色差超構透鏡所需的相位色散分布。每一列的兩幅圖對應頻率相同。Fig.4 The phase-dispersion provided by meta-unit and required for achromatic performance.(a)The phase-dispersion provided by meta-unit at different frequencies;(b) the phase-dispersion required for achromatic performance at different frequencies.Diagrams in the same column hasthe same frequencies

考察(Φr,ΔΦr)相對于(Φn,ΔΦn)的偏離程度可以更加直觀地將上述關于兩個區間的結論表現出來。定義相位色散誤差Θ為：

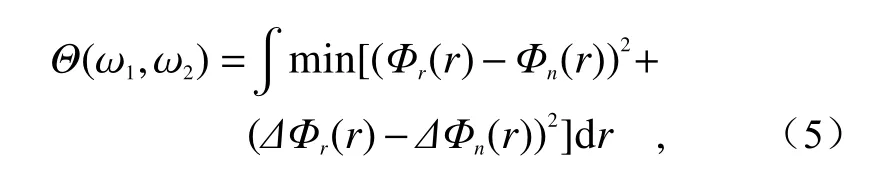
式中min 表示尋找最優的相位色散(Φr,ΔΦr)，使得r 處被積函數最小。顯然，Θ越大表示相位色散(Φr,ΔΦr)相對于(Φn,ΔΦn)偏離越大。取中心頻率ωc=342 THz (對應λ=550 nm)，在不同間隔δω下可以得到不同的頻率(ω1,ω2)=(ωc?δω,ωc+δω)。將該頻率代入式(5)，可以計算出Θ關于頻率間隔δω的分布，如圖5(a)所示。在接近坐標原點的地方Θ較小，隨著δω的增大Θ先呈現出迅速上升的趨勢，對應于之前討論的第一個區間；當Θ增加到一定程度，隨著δω的增加，其值又會呈現緩慢下降的趨勢，對應于之前討論的第二個區間。

3.2 計算驗證

基于HJ 優化算法，本文設計出對應頻率的離散消色差超構透鏡，同時計算了這些透鏡在設計頻率處的平均聚焦效率，如圖5(b)所示。計算結果驗證了之前分析得出的結論，即對于雙波長消色差超構透鏡，其聚焦效率隨兩頻率間隔的分布呈現出先下降再上升的趨勢。另一方面，對比圖5(a)和圖5(b)可以發現，效率與誤差Θ關于δω的分布幾乎呈現出一一對應的關系：當誤差Θ增大時，效率會隨之降低，而誤差Θ減小時，效率會隨之上升。這種對應關系說明用相位色散的誤差Θ來分析最終設計結果的效率是較為合理的。

上述方法可以直接推廣到三波長消色差超構透鏡的分析上。對于三波長消色差超構透鏡，假設頻率從小到大依次為ω1、ω2、ω3，此時需要考察的頻率間隔變為兩個：δω1=ω2?ω1，δω2=ω3?ω2。相位差ΔΦ也變為兩個：ω2與ω1的相位差ΔΦ1，ω3與ω2的相位差ΔΦ2。類比于雙波長的情形，用下標n表示所需要的相位色散分布，下標r表示結構能提供的相位色散分布，此時可以定義相位誤差色散為：

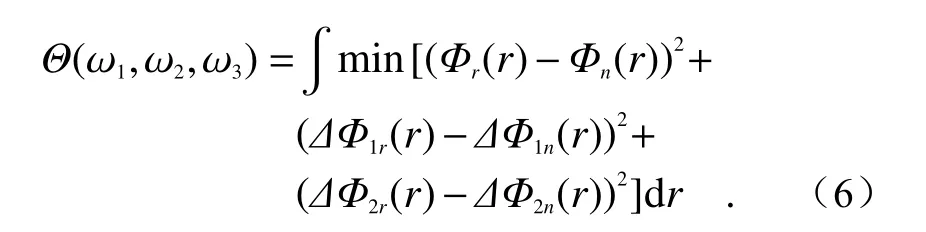
保持尺寸和數值孔徑不變，將可見光波段內不同的頻率(ω1,ω2,ω3)代入式(6)，可以計算出Θ關于頻率間隔δω1和δω2的分布，如圖5(c)所示。在接近坐標原點的地方Θ較小，隨著任意一個δω增大Θ首先呈現出迅速上升的趨勢，然后再緩慢下降。可以預測，對于三波長消色差超構透鏡，隨著兩個頻率間隔增大，其聚焦效率也呈現出先下降再上升的趨勢。

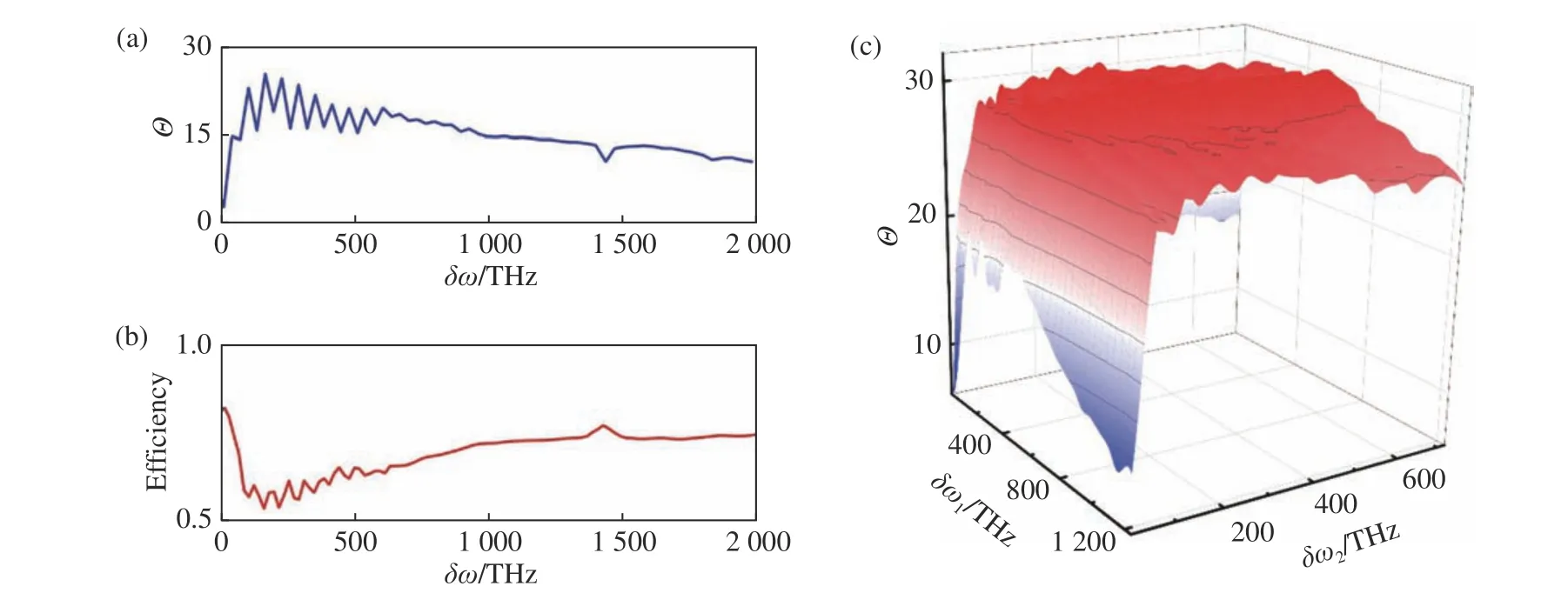
圖5 相位色散誤差及聚焦效率隨頻率間隔的分布。（a）雙波長離散消色差超構透鏡對應的相位色散誤差；（b）雙波長離散消色差超構透鏡平均聚焦效率；（c）三波長離散消色差超構透鏡對應的相位色散誤差Θ 隨頻率間隔δω1和δω2 的分布。Fig.5 The distributions of the phase-dispersion error and focus efficiency with respect to frequency interval.(a)The phasedispersion error of dual-wavelength achromatic metalens.(b)The average focus efficiency of dual-wavelength achromatic metalens.(c)The phase-dispersion error of three-wavelength achromatic metalens.

4 結 論

通過理論分析和計算驗證，本文給出了離散消色差超構透鏡和寬帶消色差超構透鏡在聚焦效率上的差異，同時也討論了離散消色差超構透鏡設計頻率的間隔對于聚焦效率的影響。從結果來看，在設計尺寸和數值孔徑較大的情況下，雙波長離散消色差超構透鏡的聚焦效率會顯著高于寬帶消色差超構透鏡，以文中給出的參數為例（直徑為360μm，數值孔徑為0.3，厚度為1μm），雙波長離散消色差超構透鏡聚焦效率約為寬帶消色差超構透鏡的4倍。如果增加消色差的波長數目，則平均聚焦效率會降低。同時，離散消色差超構透鏡的聚焦效率隨頻率間隔增大會呈現出先降后升的趨勢，不過效率整體變化不超過30%。因此，對于工作在幾個孤立波段的系統，如RGB成像系統，設計對應的離散消色差超構透鏡將會優于設計寬帶消色差超構透鏡。