配電網μPMU相量和頻率動態測量算法的研究

魏文震，王 欣，李 垚，呂 健，孫 磊

（國網山東省電力公司淄博供電公司，山東 淄博 255032）

0 引言

配電網三相不平衡現象嚴重，重載負荷情況時有發生，非線性負荷使得配電網諧波存在情況加重。因此，面對結構復雜，情況多變的配電網，應用于輸電網的傳統同步相量測量單元（Phasor Measurement Unit，PMU）技術已無法滿足相量測量精度的要求。針對配電網的特點，研制了一種適用于配電網的微型同步相量測量單元（Micro Phasor Measurement Unit，μPMU）與故障錄波裝置，該裝置相對PMU 來說體積小、成本低、安裝方便，能滿足智能電網大面積配置的需求［1-3］。由于該裝置采用的相量測量算法的動態監測性能和測量精度有限，急需要一種適合配電網的同步相量測量算法［4-8］。

傳統的PMU 測量算法通常采用靜態相量模型。配電網由于非線性負載和分布式電源的接入，使得電網結構變得復雜，頻率波動和諧波干擾等更明顯，為了更好地對幅值、相角、功率波形和頻率的動態變化進行精確測量和跟蹤，需要在傳統的相量測量算法基礎上進行改進，研究適合配電網的同步相量測量算法［9-10］。文獻［11］利用泰勒級數對時變相量進行建模，通過相量導數來修正系統動態特性對相量測量精度的影響，但計算量大，實用性不高。文獻［12］提出一種利用時域和頻域信息的動態同步相量測量算法，在低頻振蕩等動態條件下，該算法能有效降低信號動態特性對測量精度的影響。文獻［13］在相量動態模型的基礎上對傳統的離散傅里葉變化法（Discrete Fourier Transform，DFT）進行改進，提出了一種插值離散傅里葉變化法（Interpolation Discrete Fourier Transform Method，IpDFT）。文獻［14］中按照使用性能將PMU 分為P 類和M 類，前者的測量速度快，精度較差，致力于電網的保護操作；后者測量速度慢，需要擁有更高的穩態測量精度，適合測量應用。文獻［15］提出了一種同時適用于P 類和M 類的相量和頻率測量算法。該算法在對相量波動進行跟蹤時，要求測量不確定性要小，其測量結果很難滿足IEEE c37.118.1—2011 標準的要求。綜上所述，現有的同步相量測量算法是無法直接應用于配電網的。

在所研制的配電網μPMU 與故障錄波裝置的基礎上［2］，提出了一種適合配電網動態監測的同步測量算法。首先，建立動態電力信號模型，利用漢寧窗對信號模型進行加窗處理，通過IpDFT 計算出加窗信號的頻率值及二次諧波的幅值和相角，從加窗信號中去除二次諧波；然后利用所提的泰勒加權最小二乘算法（Taylor Weighted Least Square Algorithm，TWLS）對處理后的動態信號進行相量和頻率的估計，最后通過MATLAB 仿真分析驗證所提算法的動態測量性能。

1 理論分析

1.1 信號的建模

對于含噪聲干擾的動態電力信號波形模型可以表示為：

式中：?(t)為初相角；a(t)和φ(t)分別為相量的幅值和相位；Re{·}為實部的求取；b（t）為均值為0、方差為δ2的高斯白噪聲；p（t）為動態相量；f0為參考頻率。其中，φ（t）為

式中：F為瞬時頻率f和參考頻率f0間的差值，即F=(f-f0)。

在動態條件下，相量是個時變量。由于泰勒級數是表征信號動態特性的有力工具，可以將其引入到電力信號動態相量的表示中。通常情況下，信號的基波分量變化相對緩慢，對于tn時刻的動態相量p（tn）可以通過K階泰勒級數展開式來近似求解。

式中：n為不同采樣點；Nh為最后一次采樣；T為泰勒時間間隔；Δ為泰勒級數誤差；K為動態信號用泰勒級數表示的最高階次，K取值越大，p（tn）越接近于真實值。但K越大，運算量越大，算法所需時間越長，會加大噪聲對算法的影響。

將式（4）代入式（1），借助歐拉公式可以得到泰勒級數展開后的電力系統動態信號模型為

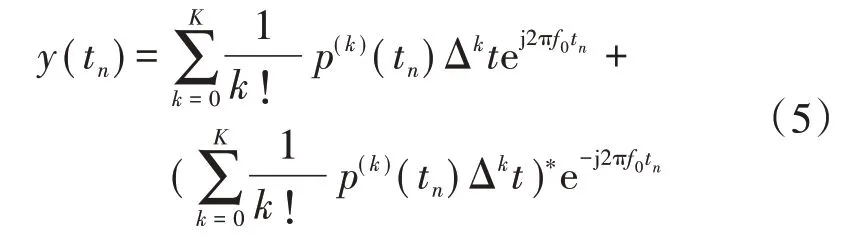
式中：(·)*為共軛。

1.2 基于動態模型的同步相量測量算法

考慮到計算速度和存儲容量等方面的限制，對于連續信號只能從中截取有限時長的樣本加以處理。信號截短由于不能完全反映原信號的頻率特性必然會對數據處理結果造成影響。因此窗函數的選取對于改善頻譜泄漏和柵欄效應對離散頻譜分析的影響非常重要。

假設信號在采樣周期T0=1/f0內的采樣數為N0，則在泰勒時間間隔T內的采樣數N=[(T/T0)N0]，[·]表示就近取奇。如果t=0 時也進行采樣，則N=2Nh+1。令第l 次采樣窗的中心位置作為參考時刻，以采樣頻率（fs=Nf0）對式（4）進行離散化處理，可得信號的離散序列為

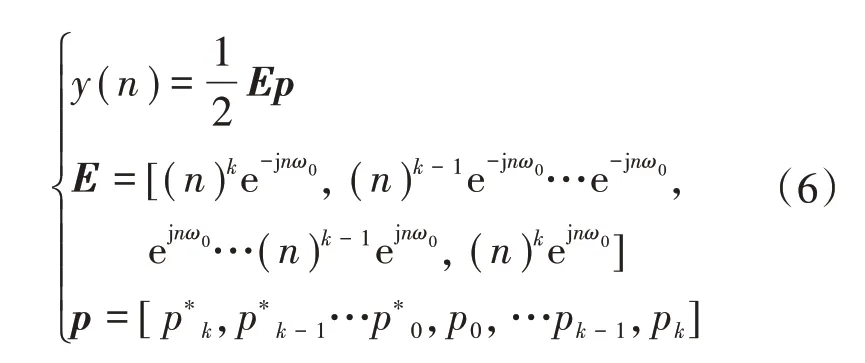
式中：ω0=2π/T0為參考角頻率；p為動態偏差因子；pk與動態相量的導數有關，為

此時，信號誤差和相量估計值誤差分別為

式中：σ為信號誤差為相量的估計偏差；y為y（n）構成的列矩陣，為

由于式（8）得到的誤差較大，考慮到泰勒誤差與Δt的取值有關，Δt越小，泰勒誤差越小。因此，可以通過對采樣區間進行加窗處理來有效減小測量誤差，則式（9）可以寫為：

式中：w(n)為所加窗的時域表示形式；W為時域窗的連續頻譜。選取的窗函數為漢寧窗，漢寧窗的時域函數表達式為

加窗后的信號為

經加窗處理后，利用TWLS法得到tn時刻的動態相量估計值為

通過上述方法可以進一步計算出與相量相關的參數，如頻偏（Frequency Deviation，FD）FD和頻率變化率（Rate of Change of Frequency，ROCOF）ROCOF，性能評價指標：相量總誤差（Total Vector Error，TVE）TVE、頻率誤差（Frequency Error，FE）FE和頻率變化率誤差（Rate of Change of Frequency Error，RFE）RFE。

1.3 動態算法的實現

在IpDFT 的基礎上提出一種TWLS 動態相量測量算法，提高了動態測量精度，并結合同步相量測量標準分析了算法的性能，TWLS 算法的流程如圖1所示。

圖1 TWLS算法的實現流程

利用TWLS 進行相量的動態估計可分為兩步：首先，通過IpDFT 對信號頻率進行初始估計，其值作為TWLS 中的參考頻率；最后，利用TWLS 法消除動態信號和相量中的干擾，達到提高測量精度的目的。對頻率估計時，對頻率進行四舍五入取整。以上算法稱為TWLS-IpDFT法。

1.4 算法的具體步驟

TWLS-IpDFT算法的具體步驟為：

1）對信號y(n)的J個波形周期進行N次采樣，n=0，1，…，N-1，其中N=Jfs/50+1。

2）對信號進行加窗處理yw(n)=y(n)w(n)，其中w(n)為漢寧窗。

4）去除二次諧波后，確定新的信號y1(n)。

采用漢寧采樣時，數據窗J至少等于3 才能保證IpDFT 對頻率的估計足夠精確。此條件在實際工程中并不影響估計性能，因為該算法頻率變化的魯棒性要比相量變化的魯棒性差。

2 仿真分析

2.1 窗函數的選取

頻譜泄漏現象與窗函數譜的旁瓣有關，如果旁瓣的幅度趨于零，使能量相對集中在主瓣，就能得到與真實值較為接近的頻譜。工程中常用的窗函數有：矩形窗、海明窗、布萊克窗和漢寧窗等［19-20］。窗函數為100時，漢寧窗的頻域仿真分析如圖2所示。

圖2 窗函數為100時漢寧窗的頻域分析

窗函數的選取原則是：窗譜主瓣要窄而高，從而提高分辨率；旁瓣幅度要小，從而減小頻譜的泄露。

考慮到旁瓣的衰減程度越大能量泄露越小，且主瓣和旁瓣、旁瓣與旁瓣間的干涉影響越小，再結合電力信號帶寬窄、干擾強的特點，選用旁瓣幅度較小、衰減程度較大的漢寧窗采樣較為合適。

2.2 性能評價標準

IEEE C37.118.1—2011 中規定了同步相量測量的測試標準：TVE、FE、RFE。通過以上標準檢查相量測量算法的時間同步性和相量計算誤差［14］。TVE、FE、RFE的定義分別為

式中：Xr(n)、Xi(n)分別為相量真實值的實部和虛部；Xr和Xi分別為相量測量值的實部和虛部；ftrue為頻率真實值；fmeasured為測量值；Δfmeasured為頻偏的測量值；Δftrue為頻偏的真實值。

2.3 仿真條件

利用MATLAB 對算法的性能進行全面測試分析，通過仿真數據對上述算法進行驗證，并利用相量測量裝置驗證算法在實際系統中應用的可行性。與傳統DFT 法進行比較，分別對幅值調制、諧波影響、信號突變3 個重要指標下的穩態性能和階躍響應下的動態性能作重點分析。仿真中，采樣頻率為10 kHz，漢寧采樣數據窗為兩個波形周期（在工頻下每個數據窗的采樣數為400）。

通過選取合適的泰勒級數展開項K，在保證測量速度的同時增加了測量精度，由表1 仿真結果可見，當K=8時，測量結果的精度可滿足要求。

表1 K=8時，TWLS-IpDFT法的同步相量測量精度

2.4 TWLS-IpDFT算法的性能分析

2.4.1 突變等動態過程的仿真分析

為測試TWLS-IpDFT 算法對突變等動態過程的響應性能，在t=20 ms時對輸入信號施加90°的相角階躍信號，并與傳統的DFT 法進行比較，各算法的階躍相應仿真曲線如圖3 所示。測試信號為

圖3 動態響應曲線

信號的初始相角?(t)為π6，參考頻率f0取IpDFT 中計算得到的加窗信號頻率值。由圖3可知，TWLS-IpDFT 算法的動態響應效果較好，比傳統的DFT 算法有著更好的相角測量精度，且跟蹤效果較好。這是由于傳統的算法把工頻作為參考頻率對相量進行測量，其動態測量效果不佳；TWLS-IpDFT 法通過IpDFT 對信號頻率進行初始估計，將估計值作為參考頻率，并選取漢寧窗作為窗函數，使得該算法動態測量效果較好。

2.4.2 幅值和相位調制對算法精度的影響

1）幅值調制。

系統正常運行時頻偏為0.1～0.2 Hz，且規定系統故障時頻偏應盡快恢復到±0.5 Hz 以內。因此，信號的參考頻率f0分別取49.5 Hz、50.5 Hz。調制頻率ft在0.1～3 Hz 內連續變化，調制幅值為10%的基波幅值。對頻率振蕩時波峰、波谷時刻的基波幅值誤差和全時段的最大相角誤差進行仿真，仿真結果如圖4所示。被測信號為

圖4 幅值調制下TWLS-IpDFT法的幅值和相角誤差

由圖4 可知，結合標準IEEE StdC37.118.1—2011：波峰幅值誤差＜0.2%，波谷幅值誤差＜0.2%，最大相角誤差＜0.5°，最大TVE＜1%［14］，當信號發生低頻振蕩時，TWLS-IpDFT法對同步相量仍能進行精確的計算，當調制頻率增加時，測量誤差有所增加，但仍保持在標準規定范圍以內。表2 為TWLS-IpDFT 法在信號幅值調制下的最大測量誤差。

表2 TWLS-IpDFT法在幅值調制下的最大誤差

2）相位調制。

相位調制情況下的被測信號設為

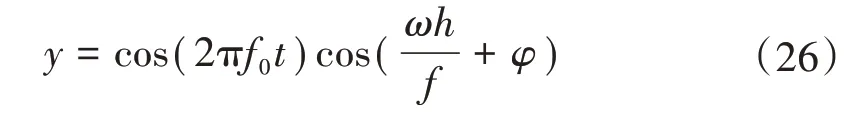
式中：ω為角速度；h為同步采樣數；φ為初相位。

相位調制幅值為0.1 rad，調制頻率為0.1～3 Hz，采樣頻率為5 400 Hz，初始相位設為π/3，h取1 024。對參考頻率分別為49.5 Hz，50 Hz，50.5 Hz 的3 種信號進行仿真測試，測量誤差如圖5 所示。根據標準中規定的TVE應在1%以內，最大FE為0.3 Hz，最大RFE為10 Hz/s，結合圖5 可知，TWLS-IpDFT 的測量誤差隨調制頻率的增加而顯著增加，但誤差比較小，能夠滿足上述標準的要求。

圖5 相位調制下TWLS-IpDFT 法的最大TVE、FE、RFE

2.4.3 諧波和噪聲抑制分析

1）諧波分析。

對電壓、電流信號注入諧波，被測信號為

對信號的相量幅值、相角誤差和頻率誤差進行仿真，仿真結果如圖6所示。

圖6 諧波干擾下TWLS-IpDFT法的幅值、相角和頻率誤差仿真

由圖6 可知，TWLS-IpDFT 法和DFT 法都受諧波的影響較大，且DFT 法不能很好地滿足TVE誤差要求，而TWLS-IpDFT 法測量精度更高，在保持跟蹤速度的同時對信號的跟蹤精度也比較高。通過對比可知，所提方法在諧波影響方面要優于傳統方法。表3為諧波影響下的最大誤差分析。

表3 諧波影響下的最大誤差

2）噪聲分析。

考慮白噪聲對TWLS-IpDFT 法的影響。當式（27）中的信號加入白噪聲b(t)時，其分布特性為N（0，0.0012），同樣使用上述兩種算法對信號進行測量，得到的TVE值如圖7所示。

圖7 噪聲干擾下的TVE誤差

2.4.4 頻率偏移仿真分析

在動態模型（1）中取幅值為1，參考頻率f0=50 Hz 的信號進行頻偏對算法測量精度的仿真分析，頻偏的范圍為-3～3Hz，信號表達式為

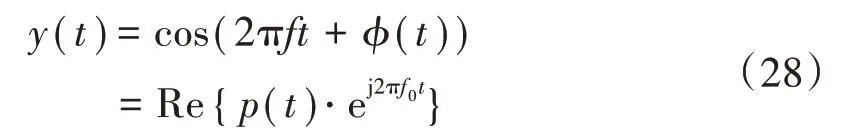
式中：p(t)為待測相量。頻偏(f-f0)分別取不同值時，對DFT 法和TWLS-IpDFT 法的相量測量結果進行比較，包括幅值、相角誤差及TVE值，仿真結果如圖8所示。

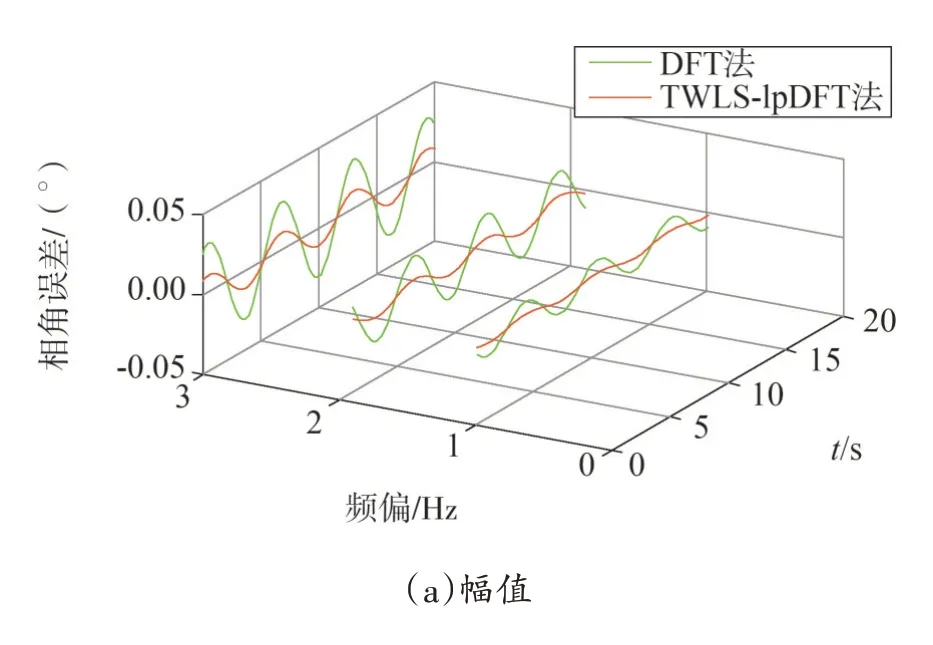
圖8 頻率偏移下的幅值、相角誤差及TVE值

由圖8 可知，隨頻偏的增加，兩種算法的測量誤差也隨之增大，但TWLS-IpDFT法的測量誤差相對較小，而DFT法的誤差增加較明顯。TWLS-IpDFT法幅值、相角及TVE誤差的波動性及總量都遠遠小于DFT法，雖然隨著頻率偏移的增大，算法的測量精度有所降低，但仍在標準規定范圍內。

3 結語

提出了一種配電網μPMU 相量和頻率測量的動態測量方法，利用漢寧窗對動態信號進行加窗處理，并對J個波形周期進行采樣，提高了算法的動態特性，減少了運算量。

將IpDFT 法計算出加窗信號的頻率值作為算法的參考頻率，計算出二次諧波的幅值和相角，得到去除二次諧波后的加窗信號，從而提高相量和頻率的測量精度。

利用TWLS-IpDFT 法對相量的幅值、相位，相量總誤差、頻率誤差和頻率變化率誤差進行估計，通過對突變狀態、調制、頻率偏移、諧波影響方面的仿真分析，結合同步測量標準，并與傳統的DFT 法進行對比，表明該算法對相量、頻率的測量精度和計算速度有一定的提高，能滿足在線計算的要求，具有一定的實用性。

綜合以上分析，所提出的TWLS-IpDFT法能夠基本滿足配電網動態同步相量測量的要求。該算法的測量精度高，運算量小，對之前μPMU 裝置的改進具有指導作用，對配電網的實時動態監測具有重要意義。后續將對原有裝置進行改進，研制一種成熟的適合配電網的高精度μPMU。