若干2021年數學奧林匹克不等式題的巧思妙證
2021-09-06 06:44:26南昌大學附屬中學330047溫偉明
中學數學研究(江西) 2021年8期
南昌大學附屬中學 (330047) 溫偉明
筆者對新近出現的一些數學奧林匹克不等式題進行了深入而廣泛的研究和探索,拈取數題寫就本文,期冀對老師與同學在教學研究中有所啟發和幫助.
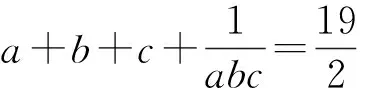
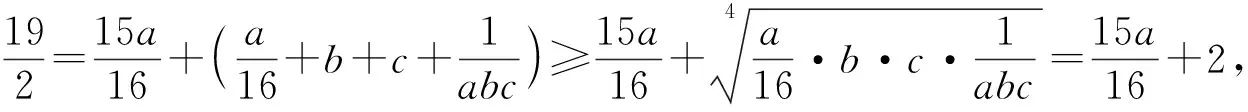
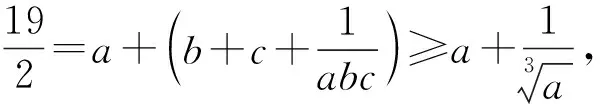
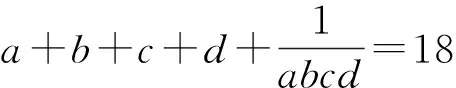
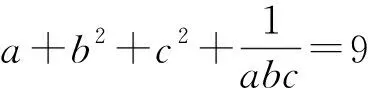
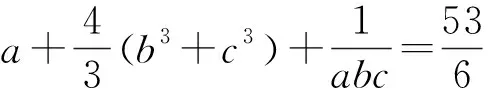
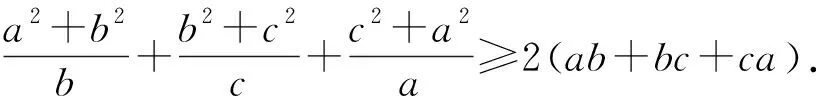
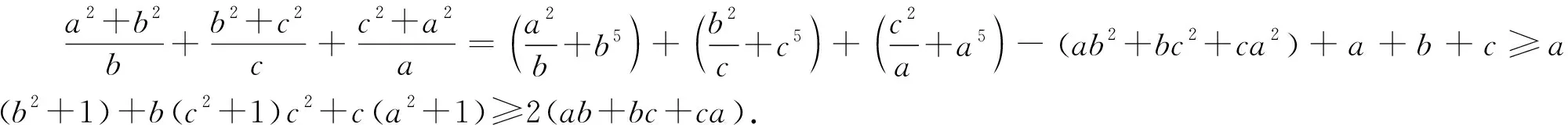
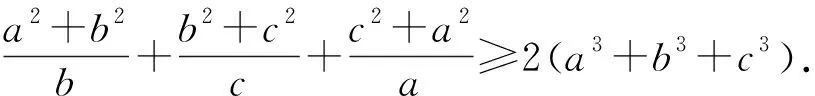
例3 (2021年西班牙數學奧林匹克試題)已知a,b,c,d是滿足a+b+c+d=0和a2+b2+c2+d2=12的實數,求abcd的最大值和最小值.
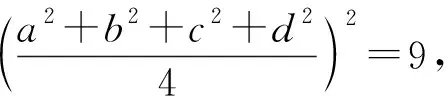
例4 (2021年菲律賓數學奧林匹克試題)已知a,b,c,d是滿足a≥b≥c≥d,a+b+c+d=13和a2+b2+c2+d2=43的實數,求證:ab≥3+cd.
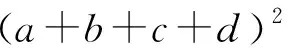
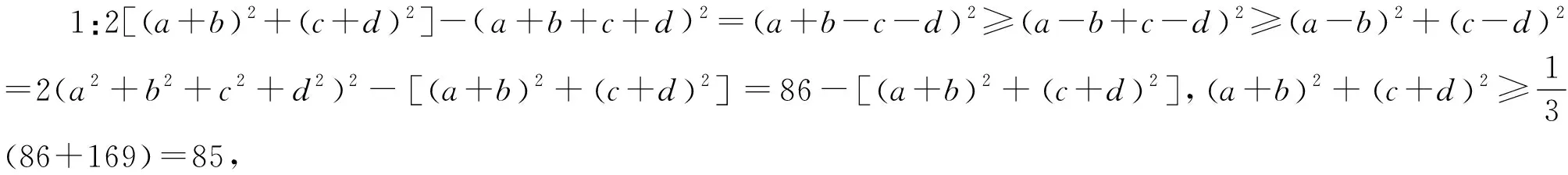
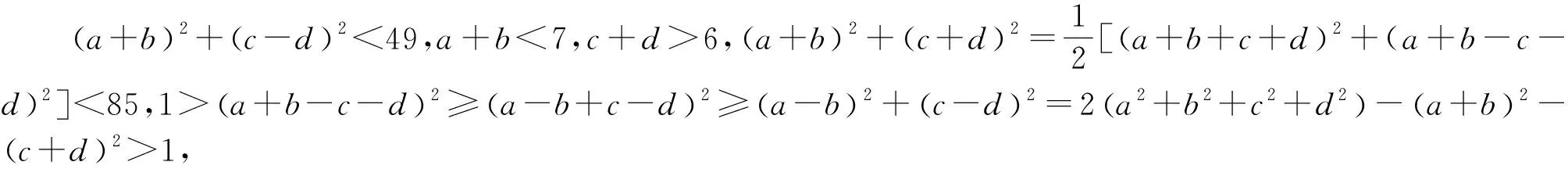
例5 (2021年烏克蘭數學奧林匹克試題)已知a,b,c是滿足a+b+c=3的非負實數,求證:(3a-bc)(3b-ca)(3c-ab)≤8.
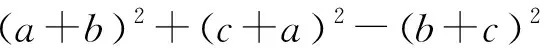
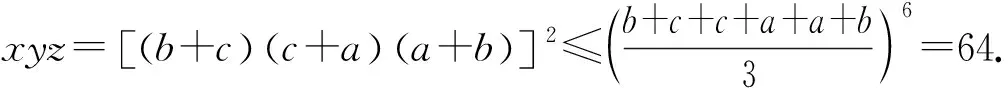
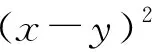
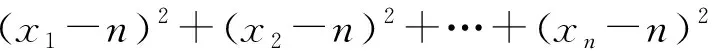

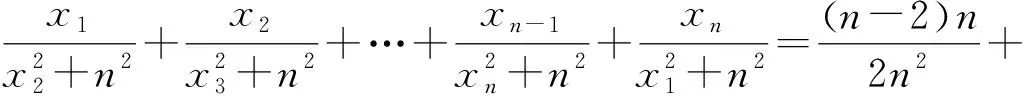
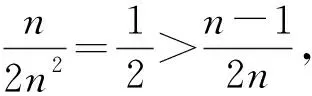
下面證明:當x1,x2,…,xn均為正數時,原不等式成立.
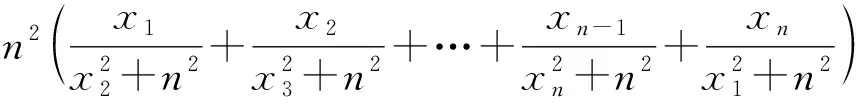
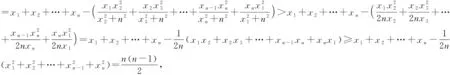
文末,我們給出一道十分漂亮的不等式題(1991波蘭數學奧林匹克試題的推廣),留給讀者探索和研討:
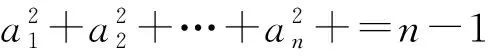
猜你喜歡
學苑創造·A版(2019年5期)2019-06-17 01:14:21
中學教學參考·理科版(2017年8期)2018-02-24 22:47:06
中學課程輔導·教學研究(2017年23期)2017-11-19 14:24:53
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
湖南城市學院學報(自然科學版)(2016年4期)2016-02-27 14:03:16
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
衛生職業教育(2014年14期)2014-05-16 05:43:02
語文教學與研究(教研天地)(2014年11期)2014-02-28 21:55:45
河南科技(2014年5期)2014-02-27 14:08:56

