基于承壓-無壓水公式的區間涌水量預測

馬文奎

（佳木斯市水利勘測設計研究院，黑龍江 佳木斯 154000）

在各種礦井涌水量的計算方法中大井法是其中使用比較普遍的一個，它是以承壓-無壓水井公式為基礎的。 但是實際的計算活動因為存在的客觀地質狀況及工作條件等的限制而具備了一些不確定性，而且會對計算數據的信度造成影響。 因此研究不確定因素對計算過程所造成的影響機制是十分有價值的，能夠有效保障所得數據的信度。 另外，對于該類計算中不確定性的描述及信度提升等研究也變成了當前的研究熱點。 其中隨機數學這項方法是在地質不確定性的研究活動里中應用最為普遍的， 在該項方法中概率密度函數獲取的準確性水平是實現可靠分析的關鍵， 但是在實際操作中因為資料的限制一般很難做到有效獲取。 本文將區間不確定性角度作為出發點，同時以非概率集合理論為理論基礎，一步步推導得到基于觀測信息及經驗公式來計算影響半徑的涌水量預測公式， 而且對變量變動范圍不確定狀態下的涌水量區間相應作了定量描述， 從而完成了傳統計算公式的轉變。

1 非概率集合理論凸模型方法

式中 Ω為正定矩陣；θ為正實數。

在有界不確定參數δ=（δi）m=（δ1，δ2， …，δm）T在{δ：δTΩ δ≤θ2}集合中變動時，能夠分別得到函數響應上下界的近似解公式φ=φmax及φ=φmin，即：

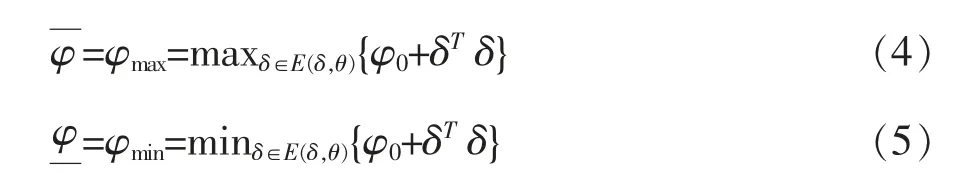
通過數學優化理論能夠證明，在{δ：δTΩ δ≤θ2}有界凸集合范圍邊界上能夠取得φmax及φmin的極值，設拉格朗日函數為：

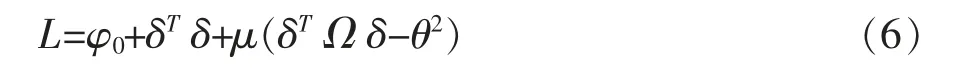
在式（6）里μ代表的是拉格朗日乘子。

取極值的必要條件是：

整理得：

把式（9）分別代入到式（4）及式（5）中能得出：

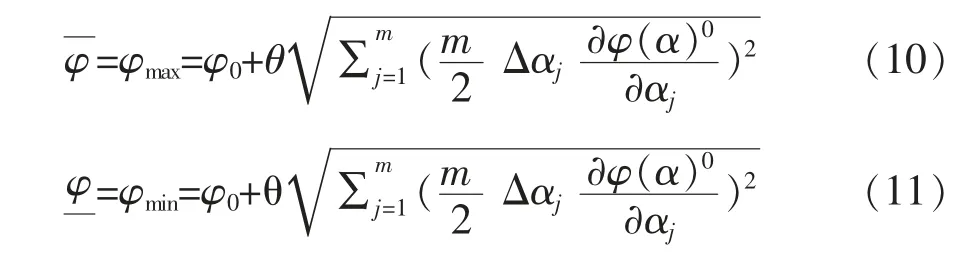
2 區間涌水量的預測公式

在各種用于地下水動力學的計算公式里， 其中一個比較重要且使用較為廣泛普遍的公式是Dupuit的承壓-無壓水公式，其表達式在被用于涌水量計算時一般為：

式中 H0為承壓含水層初始水位 （m）；Q為涌水量（m3/d）；M為含水層厚度 （m）；K為滲透系數（m/d）；rw為井的半徑（m）；邊界到外源水的距離（m）。

R一般使用的經驗計算公式為：

式（12）的涌水量計算公式對含水層的要求是要水平等厚且質量均勻，初始的水力坡度大小是零；另外還需要具備形狀為圓形的且是將抽水井作為區域中心的定水頭邊界，從而可以支持穩定流的形成。但實際的礦區環境中，大部分都不存在定頭水邊界，且很多礦區普遍具有部分陷落柱及斷層，它們具有“上三帶”及“下三帶”，采動活動存在發生“活化”的概率。 含水層結構質量的均勻性正是由于這些具有強滲透性結構的存在而下降。所以，嚴格意義上的穩定流是很難在實際的礦區開采活動中形成的。 但是通過實踐及研究發現， 地下含水層的水位可以在礦區的開采活動進行一定時間之后而逐漸變得越來越穩定，在這個時候可以近似默認其形成了穩定流狀態。在現實操作中，通常形成的都是近似狀態的穩定流，因此， 用于礦井涌水量計算的公式運行條件是近似的穩定流狀態。

在整體上，式（12）中幾個物理量H0，Q，M，K及rw不是線性關系。 以隱函數求導的法則為基礎能夠得到：

能夠得到流量對變量H0、Q、M、K及rw的導數：

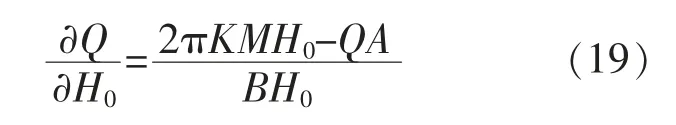
實際開采活動中，部分礦井能夠通過觀測所得數據信息及鄰近礦井狀況得到R， 因此并不需要基于式（13）來計算，在這種情況下的變量有5個：

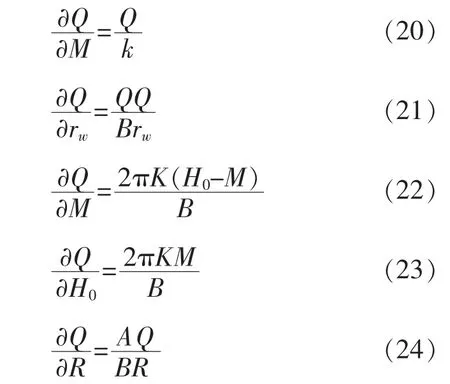
把式（16）～式（24）代入式（10）與式（11）中，能夠得出R0分別處2類處理狀況下如表1的預測公式。

表1 區間涌水量的預測公式

表1所列的預測公式考慮到H0，Q，M，K及rw這5個變量。另外，總的變化區間范圍是綜合每個變量的中心值及變化率來確定的。 變量具體的平均值及變化率是基于表格中所列的表達式給出的， 涌水量的區間響應能在不借助編程的情況下快速得出。

3 涌水量預測公式的有效性

由于式（10）～式（11）是在以數學優化理論及一階泰勒級數為基礎的情況下得出的，所以對于表1中所列出的預測公式來說， 變化率的大小一定不可以表現出無界狀態。 在實際操作中響應區間范圍邊界的確定要借助蒙特卡洛方法， 然后探究預測公式變化率界限及有效性，得到表2中的數據。

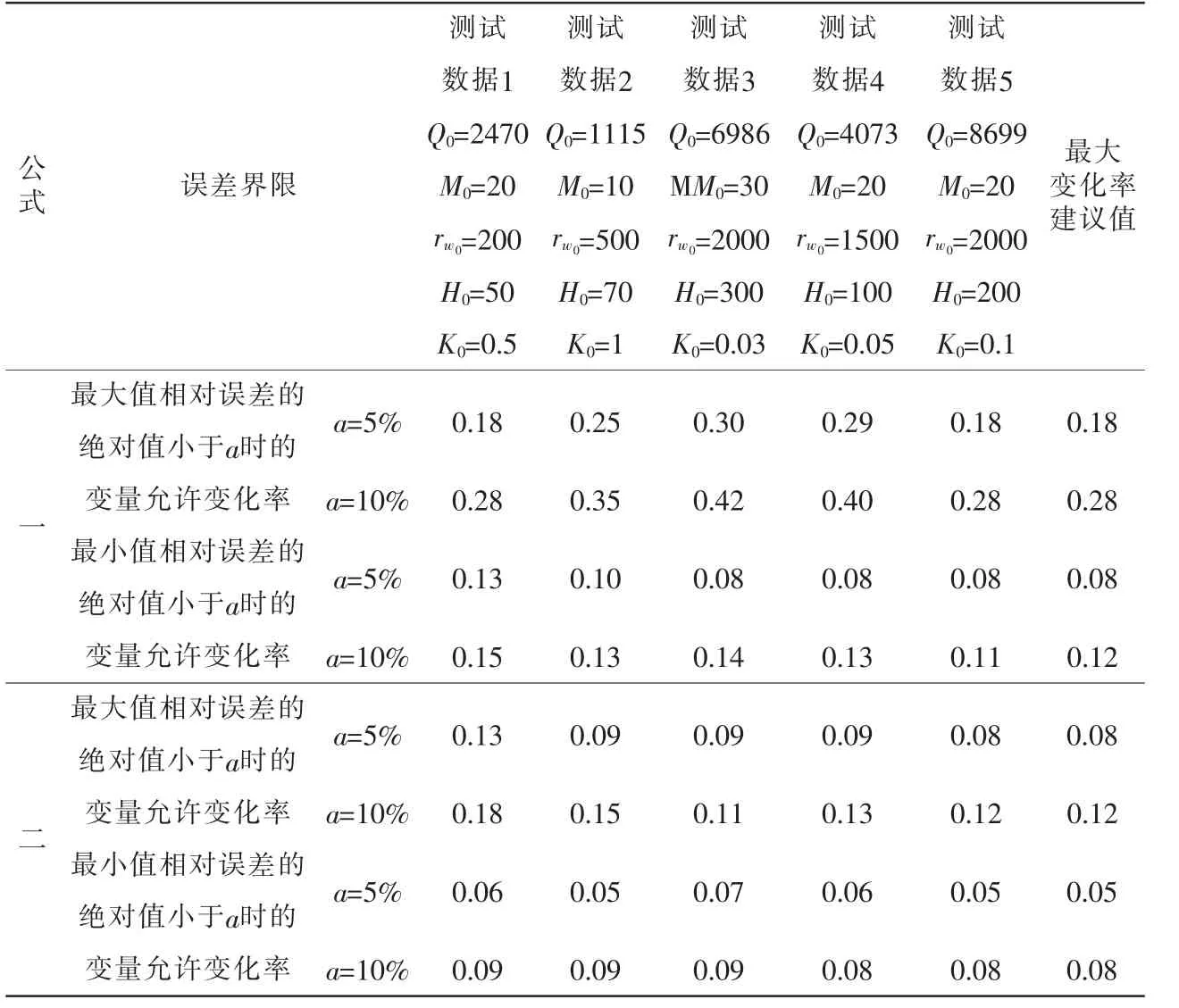
表2 不同情況下的變量變化率

表1預測公式上限值Q+和計算出的實際上限值Q這兩者的相對誤差即對應為表2中“最大值相對誤差的絕對值”，即：

在表2中，變化率在整個計算過程中的變化規律是以固定的0.01的數距遞增，從0開始增長到0.5時停止。在公式二的計算過程中，涌水量是通過式（12）運算得出的，而各組數據中的R都要通過式（13）得到的半徑值擴大4倍得出， 其余參數沒有發生變化。在表2中列出了各組測試數據在不同誤差值大小情況下的對應變化率極值。 例如在最大值的相對誤差的絕對值不超過0.05的情況下， 如果通過公式一來進行涌水量的計算，則在這種情況下式（12）的各個參數的變化率都小于0.18； 而在最大值相對誤差的絕對值不超過0.1的情況下，式（12）中的各個參數的變化率都小于0.28。

如果基于同樣的誤差數據條件，基于表2的數據結果能夠發現在這種情況下通過公式一和二得出的下限對應變量變化率是小于下限的。 這說明如果變量的變化率水平很高， 則通過公式運算得出的涌水量極小值的信度水平不如極大值。 如果要在符合一定精度需求的基礎上計算出涌水量的上下限， 一個好的選擇是對大區間進行分割， 在區間分割的基礎上在應用表1中的計算公式。

4 實例分析

某礦井的砂巖平均厚度為33m，其含水層幾乎是水平的，分布斷距是接近10m的斷層數條。 基于實驗數據能夠得知，其含水層滲透系數0.01m/d，水位標高則是+37.2m，而鄰近的礦井水位標高為+38.8m。綜合各種勘探孔數據信息發現， 該礦井砂巖具有并不均勻的富水性。 以該礦井所處地區的其他礦井施工信息為依據可得出， 在礦井開采活動進行一定時間之后，該類3煤層頂板砂巖含水層礦井是能夠產生近似穩定的涌水量的。 該礦井的開采水平是-1010m，等效半徑R是690m，首采區的形狀并不規則。 首采區的涌水量在每個變量的范圍區間具有不確定性時所對應的變動區間要通過公式一展開計算分析。

因為要同時考慮鄰近礦井所存在的客觀影響作用以及數據信息所具備的不確定性， 所以設αH0=0.05，αM=αk=αrw=0.2，水頭（m）的變動范圍是［985.3，1089.2］， 滲透系數 （m/d） 的變動范圍是［0.008，0.012］，另外等效半徑及含水層厚度（m）的變動范圍分別是［552.8，829.2］及［26，39］。 而且通過計算得出涌水量的變動范圍是 ［1036.9，3519.3］，Q0=2278.4m3/d是基于數據平均值計算得出的涌水量。基于上述情況能夠發現，雖然各個變量在該實例中的變化率極大值只為1/5，可是涌水量的實際極值與涌水量平均值仍具有十分顯著的差距，所以涌水量響應區間的分析活動是具備價值的。

圖1， 圖2均是為了能夠更深入地對通過公式一計算得到的數據相對誤差， 因變量變化率產生的變動，而呈現出具體變化規律，繪制出的數據走勢圖。

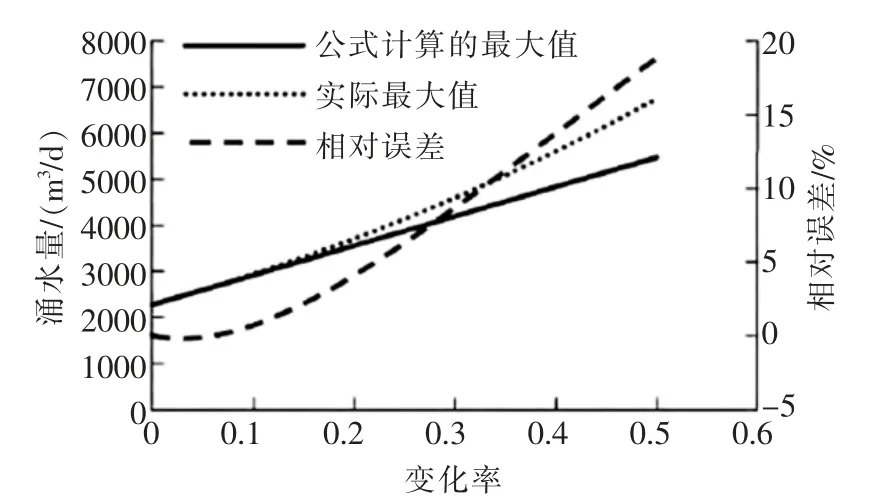
圖1 涌水量極大值相對誤差

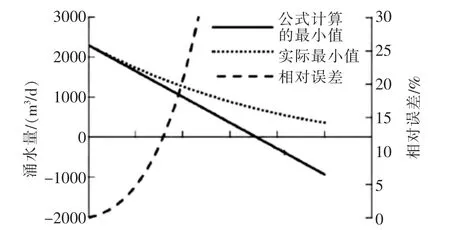
圖2 涌水量極小值相對誤差

從上述兩個數據走勢圖中能夠發現， 通過公式一得出數據結果的相對誤差，沿著變化率的改變，呈現出非線性變動特征。 其中通過圖1能夠得出，最大值的相對誤差在變化率等于0.3的情況下幾乎都能夠保持在10%范圍之內。 而通過圖2能夠得出，最小值的相對誤差在變化率等于0.15的情況下也是幾乎都能夠保持在10%范圍之內。 圖1與圖2所呈現出來的特征和表2中的數據信息是基本相同的，所以通過實例分析能夠得出應用公式一來開展各個具有一定變動區間的變量所對應的涌水量的上下限的計算是比較合理的。

5 結語

總之，本文將區間不確定性角度作為出發點，同時以非概率集合理論為理論基礎， 一步步推導得到基于觀測信息及經驗公式來計算影響半徑的涌水量預測公式， 而且對變量變動范圍不確定狀態下的涌水量區間相應作了定量描述， 從而完成了傳統計算公式的轉變。 最后通過實例的具體分析發現涌水量的區間響應是能夠比較便捷且具有較高信度地通過區間涌水量計算公式得出的， 區間不確定性解析公式能夠提供新的可用于涌水量計算的思路方法。