R134a-DMF吸收式制冷系統熱力學模型選擇

陳 鑫， 李 慧、2、3， 單明珠

(1.山東建筑大學 熱能工程學院， 山東 濟南 250101； 2.山東建筑大學可再生能源建筑利用技術教育部重點實驗室， 山東 濟南 250101； 3.山東省可再生能源建筑應用技術重點實驗室， 山東 濟南 250101)

1 概述

吸收式制冷系統利用太陽能、地熱能、低品位熱源等為驅動力，僅使用較少的電能來實現為用戶提供冷源的目標，對于全球所面臨的資源短缺及環境污染問題可以起到很好的緩解作用。本文旨在為R134a-DMF吸收式制冷系統提供基礎性研究之一，即熱力學模型的選擇。

孟學林等人[1]基于PENG-ROB狀態方程對R134a-DMF二元溶液物性進行了描述，并在此基礎上使用Aspen Plus軟件模擬了復合式制冷循環系統，得到了很好的驗證。管文潔[2]在對R1234yf-NMP二元溶液相平衡研究過程中，用NRTL熱力學模型與相平衡數據進行關聯，其計算的相對壓力平均誤差與相對最大誤差分別為1.37%與3.51%。回曉洋[3]基于PENG-ROB熱力學模型模擬了以R134a-DMF為工質對的吸收式制冷循環系統，模擬系統的性能結果分別與H2O-LiBr、NH3-H2O吸收式制冷系統進行了對比。鄧如雷[4]基于測定的R134a-DMF相平衡數據，分別對PENG-ROB與NRTL熱力學模型進行回歸處理，兩種熱力學模型均能得到很好的回歸結果。Han等人[5]進行R134a-DMF二元溶液溶解度測定時，其測得的實驗數據與活度系數模型NRTL進行關聯，其平均相對誤差及最大誤差均在誤差允許范圍內。Zehioua等人[6]對R134a-DMF二元溶液相平衡實驗數據關聯發現，PENG-ROB與合適的混合規則及NRTL聯立時能夠更好地描述相平衡實驗數據。以上學者進行實驗數據與熱力學模型關聯時對熱力學模型的選擇均沒有詳細介紹，且應用于R134a-DMF二元溶液的各種熱力學模型的相對誤差對比研究相對較少。

本文以R134a-DMF二元溶液為研究對象，首先使用熱力學模型決策樹初步選擇適合該二元溶液的熱力學模性，然后基于Zehioua等人[6]測定的部分氣液平衡(Vapor Liquid Equilibrium，VLE)實驗數據，利用Aspen Plus軟件對熱力學模型參數進行回歸，由于Aspen Plus軟件內包含各種熱力學模型且帶有回歸功能，可直接輸入實驗數據計算方程的回歸結果，最后根據回歸結果確定最優熱力學模型。

2 決策樹法熱力學模型的選擇

2.1 熱力學模型決策樹

熱力學模型決策樹是由Carlson于1996年提出的，該方法在熱力學模型選取過程中得到了眾多學者的認可，決策樹法熱力學模型的選擇流程見圖1。從圖中可以看出，熱力學模型選擇可分為以下幾步。

圖1 熱力學模型決策樹

① 確定分子的極性。分子極性越大，分子間的交互作用越強。混合物內有極性組分的存在，就應該選擇極性分支。

② 此時所需確定的參數取決于第一步參數的確定。如果混合物是極性的，必須考慮混合物內是否存在電解質組分，若存在電解質組分，則選擇ELECNRTL，否則進行步驟③；如果混合物全部為非極性的，必須考慮混合物內是否全部為真實組分，若全部為真實組分，則選擇PENG-ROB、RK-SOAVE、PR-BM、LK-PLOCK、RKS-BM、SRK，否則進行步驟④。

③ 對于極性非電解質混合物，需考慮混合物壓力范圍。該類混合物壓力范圍以100 kPa為臨界點。當壓力小于等于100 kPa時，進行步驟⑤；當壓力大于100 kPa時，考慮混合物是否存在二元交互作用參數，存在二元交互作用參數選擇SR-POLAR、PRWS、RKSWS、PRMHV2、RKSMHV2，不存在二元交互作用參數選擇PSRK、RKSMHV2。

④ 對于非極性虛擬和真實組分混合物，需考慮混合物壓力范圍，該類混合物壓力范圍以大氣壓為臨界點。壓力大于101.325 kPa時，選擇CHAOSEA、BK-10、GARYSON；壓力小于101.325 kPa時，選擇BK-10、IDEAL。

⑤ 對于壓力小于等于100 kPa的極性非電解質混合物，當該類混合物不存在二元交互作用參數且不為液液平衡時選擇UNIFAC、UNIF-LBY、UNIF-DMD；該類混合物不存在二元交互作用參數但為液液平衡時選擇UNIF-LL；該類混合物存在二元交互參數且為液液平衡時選擇NRTL、UNIQUAC；該類混合物存在二元交互作用參數但不為液液平衡時選擇WILSON、NRTL、UNIQUAC。

2.2 確定熱力學模型決策樹判定參數

熱力學模型決策樹判定參數即決策樹內的判定條件，分別由是否為極性、是否為真實或虛擬組分、是否為電解質、是否滿足壓力范圍、是否存在交互作用參數及液液平衡組成。本文熱力學模型決策樹參數通過Aspen Plus軟件以R134a-DMF為研究對象，來完成熱力學模型選擇過程中所需決策樹判定參數的確定。

基于Aspen Plus軟件內的分子結構功能，確定R134a與DMF的分子結構進而確定分子極性。R134a的分子結構見圖2，DMF的分子結構見圖3。根據二者的分子結構可知，R134a-DMF二元溶液為極性體系且存在分子間交互作用，溶液內不存在游離態離子，故不為電解質溶液。

圖2 R134a的分子結構

圖3 DMF的分子結構

基于Aspen Plus軟件確定R134a-DMF二元溶液VLE實驗壓力范圍，VLE實驗壓力一般不超過R134a在各溫度下的飽和蒸氣壓，通過Aspen Plus軟件獲得R134a的飽和蒸氣壓曲線來確定壓力范圍。在Aspen Plus軟件中，選擇PENG-ROB物性方法，使用軟件內純物質分析功能，選擇變量為飽和壓力與溫度，即可得到R134a的飽和蒸氣壓曲線，見圖4。

本文研究對象為應用于吸收式制冷系統的R134a-DMF二元溶液。若吸收式制冷系統熱源來自太陽能集熱系統，該系統在發生器內換熱后，發生溫度約80 ℃。假定吸收式制冷系統高壓側(發生器側)溫度為80℃，高壓側為吸收式制冷系統壓力最高側，同時對應溫度最高側，根據系統最高溫度確定系統的壓力范圍。由圖4可確定溫度在80 ℃時，對應最大壓力為2.7 MPa，故二元體系壓力范圍為0～2.7 MPa，VLE實驗過程中存在氣液兩相。

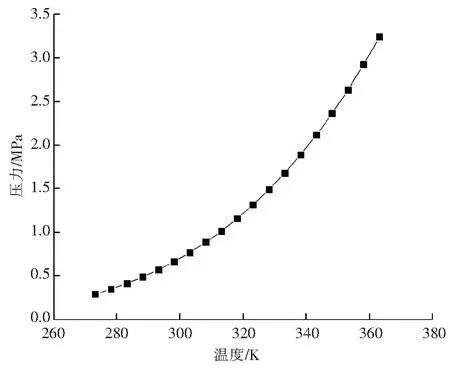
圖4 R134a的飽和蒸氣壓曲線

綜上所述，R134a-DMF二元溶液的熱力學模型決策樹參數為極性體系、非電解質且壓力范圍為0～2.7 MPa，分子間有交互作用且存在氣相與液相兩種狀態。

2.3 確定熱力學模型

根據上文確定的R134a-DMF二元溶液熱力學模型決策樹參數，最終選擇熱力學模型為：壓力小于等于100 kPa時，熱力學模型為WILSON、NRTL、UNIQUAC；當壓力大于100 kPa時，熱力學模型為PRWS、RKSWS、PRMHV2、RKSMHV2。經查閱文獻[7]，R134a-DMF二元溶液常使用的物性方法為PENG-ROB與NRTL，Zehioua等人[6]使用PRMHV2對R134a-DMF二元溶液相平衡數據進行了擬合，故本文在上述熱力學模型中選擇PENG-ROB、NRTL、PRMHV2基于R134a-DMF二元溶液VLE實驗數據進行擬合，并對擬合結果進行比較。

3 熱力學模型回歸

PENG-ROB狀態方程的表達式見文獻[8]，NRTL熱力學模型的表達式見文獻[9]，PRMHV2模型的表達式見文獻[10]。在實際應用中，為了能夠更好地描述溶液的相平衡行為，通常不會直接使用熱力學模型的原參數，而是基于VLE實驗數據，對方程進行參數的擬合，擬合出更加接近于實際工程的新參數。基于Zehioua等人[6]測定的R134a-DMF二元溶液VLE實驗數據，使用Aspen Plus軟件分別對PENG-ROB、NRTL與PRMHV2這3種熱力學模型進行擬合，并對比擬合結果，實驗數據溫度與壓力范圍分別為303.3 K、353.24 K及0～2.7 MPa。

基于上述實驗數據，利用Aspen Plus軟件內的回歸功能，對模型進行參數回歸。在Aspen Plus中選擇PENG-ROB物性方法，輸入實驗數據，設置回歸過程PENG-ROB物性方法所需回歸參數后，運行軟件內回歸功能，得到回歸曲線見圖5，圖中x表示系統內液相R134a摩爾分數、y表示系統內氣相R134a摩爾分數。同樣對熱力學模型NRTL及PRMHV2進行參數回歸，結果見圖6和圖7。回歸過程中，回歸參數的選取依據所選取熱力學模型而定，不同熱力學模型選取的參數不同。

圖6 303.3 K下基于NRTL熱力學模型回歸數據與實驗數據對比

圖7 303.3 K下基于PRMHV2熱力學模型回歸數據與實驗數據對比

從圖5～7可知，基于實驗數據回歸后的熱力學模型與實驗數據之間的誤差均很小。利用Aspen Plus軟件內Regression功能對溫度為353.24 K時的實驗數據進行回歸，并結合溫度為303.3 K下的回歸結果，計算出上述3種熱力學模型分別在溫度為303.3 K與353.24 K時的回歸相對誤差，計算方法見式(1)。相對誤差見圖8。

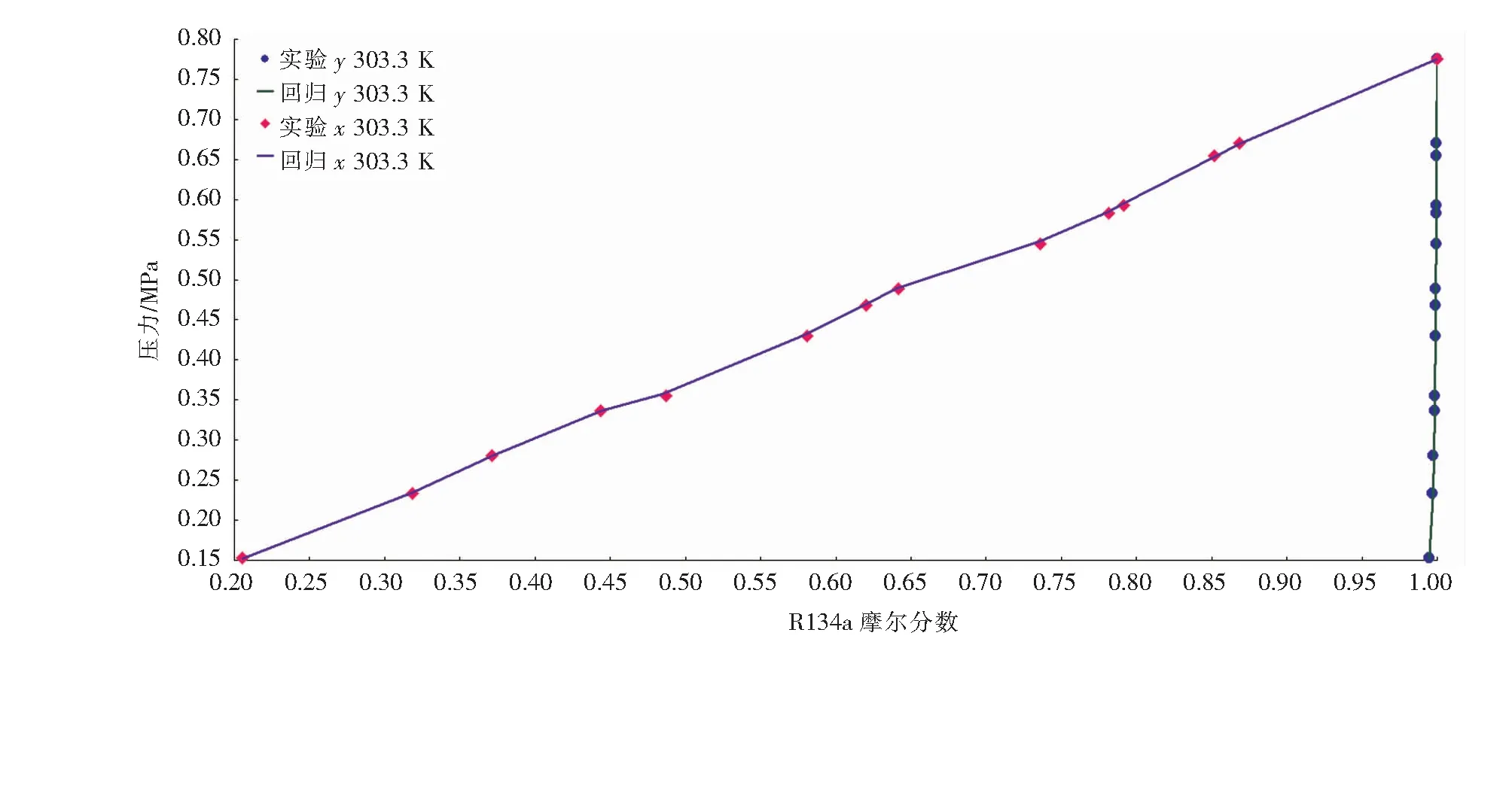
圖5 303.3 K下基于PENG-ROB熱力學模型回歸數據與實驗數據對比

(1)

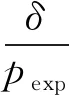
δ——誤差，MPa

pext——估算壓力，MPa

pexp——實驗壓力，MPa

由圖8可知，3種熱力學模型通過參數回歸后，與實驗值產生的相對誤差均在2%以內，同時可以看出在溫度為303.3 K與353.24 K時，回歸后的PENG-ROB熱力學模型的相對誤差最小。回歸后的NRTL熱力學模型除去溫度為353.24 K時兩個相對誤差最高點外，其相對誤差值偏高于回歸后的PENG-ROB熱力學模型。回歸后的PRMHV2熱力學模型，在溫度為303.3 K與353.24 K時，除個別點相對誤差低于回歸后的NRTL熱力學模型外，其相對誤差值為3種回歸后的熱力學方法中的最大值。根據式(2)計算平均相對誤差，回歸后的3種熱力學模型的平均相對誤差見表1。

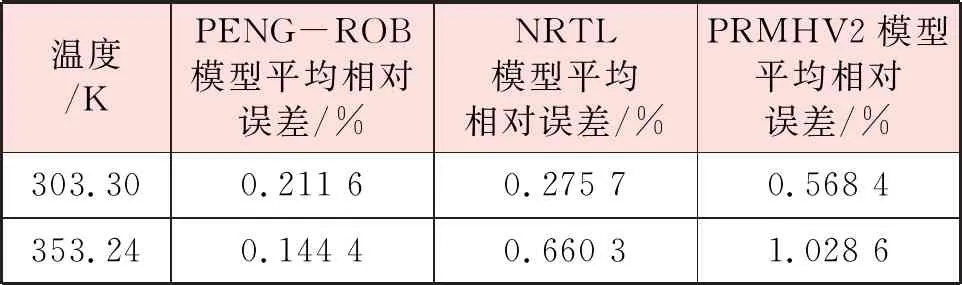
表1 3種熱力學模型回歸壓力平均相對誤差

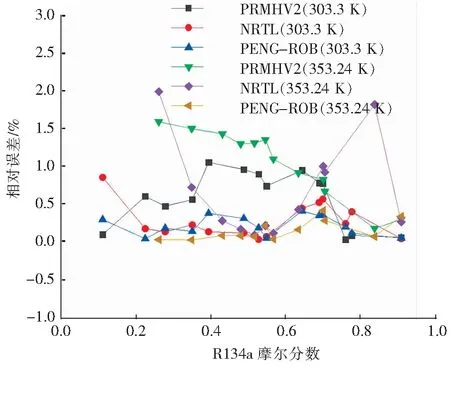
圖8 303.3 K與353.24 K下三種熱力學模型的回歸相對誤差

(2)

N——總相對誤差數

i——計數變量

δi——第i組誤差，MPa

pexp,i——第i組實驗壓力,MPa

由表1可知，3種熱力學模型回歸壓力的平均相對誤差，PENG-ROB最小，NRTL次之，PRMHV2最大，故選取R134a-DMF二元溶液熱力學模型為PENG-ROB，其回歸參數為-0.000 138 782，該值可直接應用于接下來的吸收式制冷循環系統的模擬過程中。

4 結論

以R134a-DMF二元溶液為研究對象，基于Aspen Plus軟件，對該二元溶液在溫度303.3 K、353.24 K下，應用于吸收式制冷模擬的熱力學模型的選擇進行了研究。

① 基于Aspen Plus軟件分析了二元溶液的分子結構及制冷劑R134a的飽和蒸氣壓曲線，確定了R134a-DMF二元溶液為極性體系及在制冷系統內的運行壓力范圍，按照熱力學模型決策樹的方法，根據該二元混合物的極性、壓力范圍等判定條件初步確定了PENG-ROB、NRTL與PRMHV2共3種熱力學模型。

② 結合R134a-DMF二元溶液的氣液平衡實驗數據，基于Aspen Plus軟件，對3種熱力學模型進行了回歸。回歸后的PENG-ROB熱力學模型的壓力平均相對誤差最小，故選擇PENG-ROB熱力學模型作為研究以R134a-DMF為工質對的吸收式制冷循環系統的物性方法，回歸后的二元交互作用參數為-0.000 138 782。