氯鹽環境下鋼筋銹蝕損傷混凝土應力應變本構模型

鐘小平, 戴仁禮, 袁承斌, 夏 晉, 彭藍鴿

(1.揚州大學 建筑科學與工程學院, 江蘇 揚州 225127; 2.揚州大學 水利科學與工程學院, 江蘇 揚州 225009; 3.浙江大學 結構工程研究所, 浙江 杭州 310058)

對于氯鹽環境下的鋼筋混凝土結構,氯鹽侵蝕及由此引起的鋼筋銹蝕膨脹力都將使混凝土產生損傷[1-3].混凝土受到損傷后,其應力-應變本構關系將發生改變,而鋼筋銹蝕損傷混凝土應力-應變本構關系是研究服役鋼筋混凝土結構剩余承載力和變形性能的基礎,也是服役結構非線性有限元分析時必不可少的本構關系.

然而,目前有關氯鹽環境下鋼筋銹蝕損傷混凝土應力-應變本構關系的研究還很少.先前的研究主要關注了不同環境條件下(溫度、濕度、干濕交替等)氯鹽單因素作用對混凝土的侵蝕特性[4-5]、損傷機理[6-7]、抗壓強度[8]、抗折強度[9]、動力學特性[10-11]及變形性能[12]等方面.研究表明,氯鹽腐蝕初期對混凝土抗壓強度有一定益處,但后期抗壓強度、抗折強度、動力學特性等均有明顯降低.這些研究成果為深入分析氯鹽腐蝕混凝土的損傷機理及力學性能退化規律提供了理論基礎.然而,實際氯鹽環境中的混凝土結構損傷尤其是鋼筋混凝土梁、柱等的損傷,除了氯鹽腐蝕造成的損傷以外,由氯鹽侵蝕引起的鋼筋銹蝕膨脹力作用于混凝土,也會導致混凝土產生開裂、剝落等損傷[13-14],即混凝土損傷是氯鹽腐蝕及由此引起的鋼筋銹蝕膨脹損傷共同作用的結果,僅考慮氯鹽腐蝕損傷部分不能真實反映混凝土力學性能的退化規律.鑒于此,本文通過實驗室加速腐蝕試驗,對氯鹽環境下鋼筋銹蝕損傷混凝土的力學性能進行試驗研究,建立氯鹽環境下鋼筋銹蝕損傷混凝土應力-應變本構模型,以期為服役鋼筋混凝土結構抗力退化及結構非線性有限元分析提供準確的材料性能參數.

1 試驗

1.1 原材料及試件設計

水泥采用42.5級普通硅酸鹽水泥;粗骨料采用粒徑為5～20mm連續級配的碎石;細骨料為天然河砂,細度模數為2.49;水為普通自來水.混凝土配合比見表1.

表1 混凝土配合比

采用150mm×150mm×300mm的棱柱體試件.根據鋼筋混凝土構件的布筋特點,在試件的4個角上內置直徑為16mm、長度為240mm的HRB400級鋼筋,如圖1所示.鋼筋銹蝕對混凝土試件造成的損傷程度以鋼筋銹蝕率來表征,設計鋼筋理論銹蝕率ρ為0%(未銹蝕,對照組)、3%、6%、9%,每組制作6個試件,其中3個用于測定混凝土的軸心抗壓強度和應力-應變全曲線(A組),另外3個用于測定混凝土的彈性模量(B組).澆筑試件之前,在鋼筋末端接上導線,用于對試件進行通電加速腐蝕試驗.試件澆筑成型24h后拆模,在(20±2)℃和相對濕度95%以上的標準養護室中養護至28d,之后進行加速腐蝕試驗.

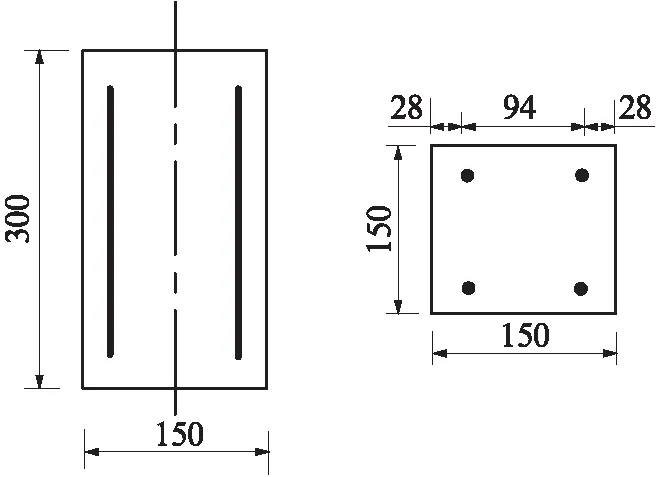
圖1 鋼筋布置示意圖Fig.1 Schematic diagram of steel bar arrangement(size：mm)

1.2 加速腐蝕試驗

將試件放置于質量分數為5%的氯化鈉溶液中進行“恒電流-氯鹽干濕循環”加速腐蝕試驗.干濕循環周期采用14d,干濕循環比例為1∶1,即干7d濕7d,干燥時室內平均氣溫15℃,平均相對濕度70%左右.加速銹蝕過程中將穩壓直流電源的負極連接于包裹在試件表面的不銹鋼絲網上,待銹蝕鋼筋與電源的正極連接,濕態時通電開始,干態時通電停止.腐蝕電流密度采用i=0.2mA/cm2,銹蝕鋼筋表面積選取所有待銹蝕鋼筋表面積之和,計算得到每個試件所需的通電電流大小I=0.11A.根據設計的鋼筋理論銹蝕率ρ,采用Faraday腐蝕定律計算得到預期的通電時間t、干濕循環時間tw及干濕循環次數N,結果見表2.分別達到各自的通電時間后,加速腐蝕試驗結束.

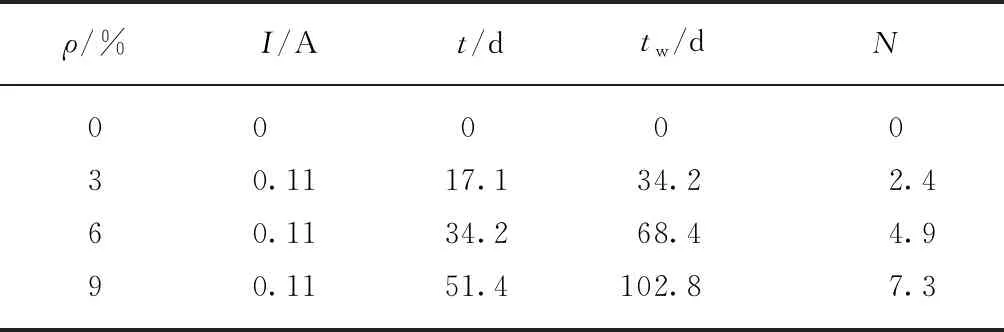
表2 鋼筋銹蝕損傷混凝土試件加速腐蝕參數計算結果

1.3 加載試驗及鋼筋銹蝕率測定

鋼筋銹蝕損傷混凝土應力-應變全曲線及彈性模量測試在YAW-G3000kN微機控制電液伺服高剛度巖石混凝土試驗機上進行.試件上、下端安裝激光位移計,采用等變形加載.應力-應變全曲線測試時,上升段以0.2mm/min的速率加載,達到峰值應力后,下降段以0.15mm/min的速率進行卸載,直至曲線逐漸平穩試驗結束;彈性模量測試時,彈性階段以0.15mm/min的速率加載至變形為0.3mm,然后以同樣的速率卸載至變形為0.1mm,如此進行3次加載,在最后一次加載完成后,以0.2mm/min 的速率加載至峰值,達到峰值應力后,下降段以0.15mm/min的速率進行卸載,直至曲線逐漸平穩試驗結束.試件荷載及總變形等數據由計算機自動采集并記錄.

應力-應變全曲線及彈性模量測試完成后,取出銹蝕鋼筋,除銹、烘干處理后,測定鋼筋銹蝕后質量,然后采用失重法計算獲得全曲線組試件(A組)和彈性模量組試件(B組)的實測平均銹蝕率ρc,結果如表3所示.

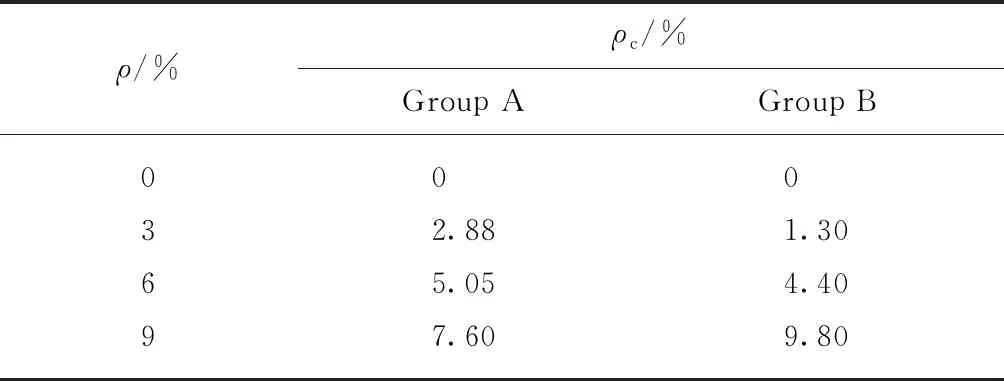
表3 鋼筋實測平均銹蝕率統計表

2 結果與分析

2.1 鋼筋銹蝕損傷混凝土試件外觀

氯離子侵入混凝土內部,在使混凝土遭到腐蝕的同時引發鋼筋銹蝕,當鋼筋銹蝕膨脹力超過混凝土抗拉強度后,混凝土被脹裂.觀察損傷試件表觀狀況(如圖2所示)發現,沿鋼筋長度方向,試件表面均出現了不同程度的順筋銹脹裂縫,并且隨著鋼筋銹蝕率的增加,銹脹裂縫逐漸貫通,裂縫寬度逐漸增大,裂縫處有銹蝕產物溢出.

圖2 損傷試件表觀狀況Fig.2 Surface conditions of damaged specimens

2.2 破壞過程與形態

觀察未銹蝕和銹蝕損傷混凝土試件的加載過程,發現二者的破壞過程與破壞形態并不完全相同.未銹蝕損傷試件加載初期應力-應變按一定比例增長,隨著荷載的增大,試件逐漸進入彈塑性階段,當接近峰值應力時,試件中部出現少量豎向細微裂縫,達到峰值應力后,承載力緩慢下降,試件出現多條不連續的豎向裂縫,裂縫尖端逐漸貫通形成斜向破裂面.

對于銹蝕損傷混凝土試件,由于加載前已經受到損傷,存在與受力方向大致平行的銹脹裂縫,因此,從開始加載到試件破壞的整個受力過程中,銹脹裂縫寬度逐漸增大,應變增長較快.臨近峰值荷載時,棱柱體試件中部相繼出現了豎向細微加載裂縫,并向試件兩端發展,試件端部的混凝土開始剝落.達到峰值應力后,銹脹裂縫和試件中部的加載裂縫寬度發展迅速,橫向變形加劇,棱柱體沿銹脹裂縫和加載裂縫被劈裂成幾個小柱體,這些微小柱體繼續失穩破壞,棱柱體的承載力逐漸降低,核心混凝土被壓壞,最后形成以銹脹裂縫為主的破裂面.

2.3 應力-應變全曲線

2.3.1實測應力-應變全曲線

將實測荷載和縱向位移分別換算為應力σc和應變εc,得到不同鋼筋銹蝕率試件的應力-應變全曲線(見圖3),每條曲線均取自3個試件的平均值.由圖3可見：不同鋼筋銹蝕率試件應力-應變全曲線形狀及特征大體相同,均由上升段和下降段組成;在應力-應變全曲線上升段,隨著鋼筋銹蝕率的增加,應力-應變曲線的斜率逐漸減小,峰值應變增大,峰值應力降低,說明銹蝕損傷對混凝土的強度和變形均產生了一定的影響;當應力超過峰值應力后,曲線進入下降段,不同鋼筋銹蝕率試件的強度并不完全消失,隨著應力的減小(卸載),應變仍然增加.

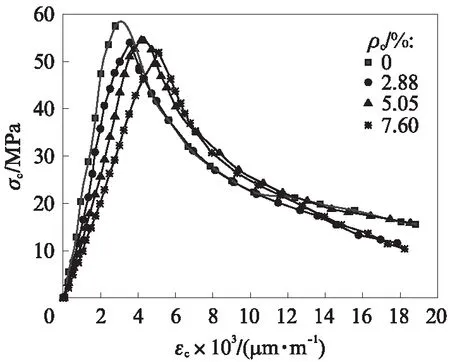
圖3 不同鋼筋銹蝕率試件的應力-應變全曲線Fig.3 Stress-strain curves of specimens with different corrosion ratios

2.3.2力學性能指標

表4給出了各混凝土試件的峰值應力σ0,c、峰值應變ε0,c和極限應變εcu,c.其中,極限應變εcu,c取鋼筋銹蝕損傷混凝土應力-應變全曲線下降段0.85倍峰值應力處對應的應變值[15-16].

表4 各混凝土試件的峰值應力、峰值應變和極限應變

由表4可見,鋼筋銹蝕損傷混凝土的峰值應力σ0,c均低于未銹蝕損傷試件,當鋼筋實測平均銹蝕率ρc從0增加到2.88%時,峰值應力σ0,c降低速率較快,較未銹蝕損傷試件降低了6.1%;隨著ρc的增加,σ0,c降低速率減小,當ρc達到7.60%時,鋼筋銹蝕損傷混凝土的峰值應力σ0,c較未銹蝕損傷試件降低了9.8%.分析原因：鋼筋銹蝕作用初期,銹蝕膨脹力使混凝土內部產生了微裂縫,并已發展到試件表面形成了可見的銹脹裂縫,見圖2(b),試件由里及表受到損傷,外圍脹裂部分混凝土對核心混凝土的橫向約束能力快速減弱,其受力狀態基本上相當于核心區域混凝土的受力狀態,因而峰值應力降低較快;隨著腐蝕時間延長,ρc增加,抗壓強度主要由核心混凝土提供,由于銹脹力尚未使面積較大的核心混凝土脹裂,銹蝕對核心混凝土強度降低的影響減小,因而峰值應力降低速率減小.由表4還可以看出,試件峰值應變和極限應變隨著ρc的增加,基本呈線性增長.當ρc達到7.60%時,試件峰值應變和極限應變較未銹蝕損傷試件分別增長了81.7%和64.6%.可見,鋼筋銹蝕損傷對試件峰值應力、峰值應變、極限應變均有較大的影響.通過對表4中試驗數據進行擬合,得到了峰值應力、峰值應變、極限應變與實測平均銹蝕率之間的關系：

σ0,c=57.047-0.6708ρc,ρc≤7.6%

(1)

ε0,c=0.0028+0.0003ρc,ρc≤7.6%

(2)

εcu,c=0.0037+0.0003ρc,ρc≤7.6%

(3)

式(1)～(3)的擬合相關系數分別為0.8684、0.9937、0.9756,可見擬合結果較好.

2.3.3應力-應變全曲線方程

對實測的應力-應變全曲線進行無量綱化處理,橫坐標采用εc/ε0,c表示,縱坐標采用σc/σ0,c表示,如圖4所示.

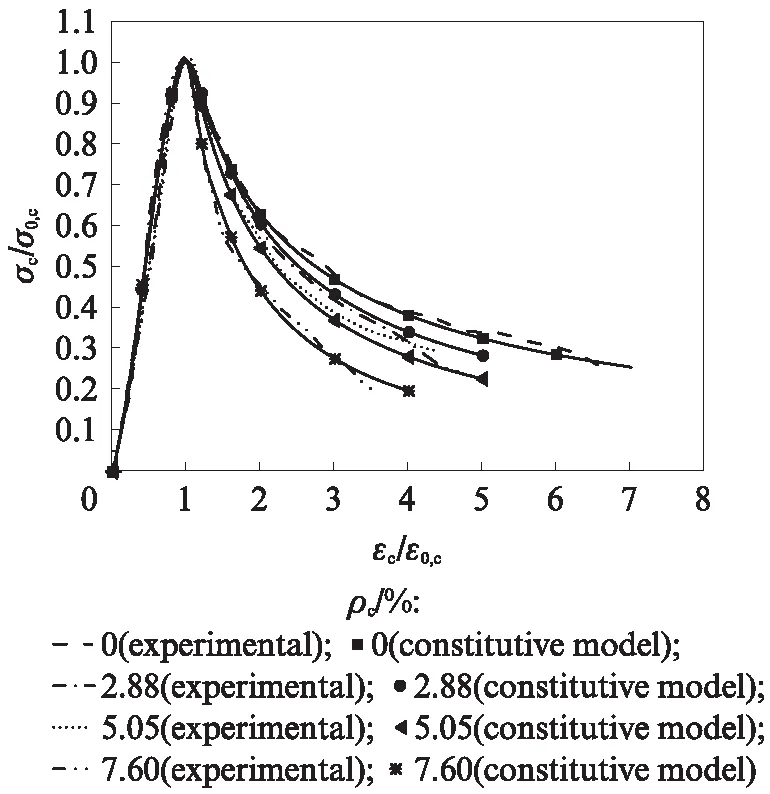
圖4 本構模型與實測曲線對比Fig.4 Comparison of constitutive models with experimental curves

由圖4可見,實測曲線的上升段和下降段有明顯的區別,上升段各曲線基本重合,近似線性發展;達到峰值應力后,隨鋼筋實測平均銹蝕率增加,曲線下降段坡度變陡,說明鋼筋實測平均銹蝕率越大,試件脆性越明顯.根據曲線上升段和下降段各自的特點,分別選用不同的函數,采用最小二乘法擬合試驗結果，得到應力-應變全曲線本構模型.

上升段[17]:

y=ax+(3-2a)x2+(a-2)x3, 0≤x≤1

(4)

下降段:

y=bxβ,x>1

(5)

式中:y=σc/σ0,c;x=εc/ε0,c;a為曲線上升段控制參數;b、β為曲線下降段控制參數.

通過擬合分析,得到曲線上升段和下降段控制參數a、b和β隨ρc變化的表達式：

a=0.0035ρc2-0.017ρc+0.641

(6)

b=-0.0043ρc2+0.0271ρc+1.0297

(7)

β=-0.0043ρc2-0.026ρc-0.7182

(8)

為了驗證本文給出的應力-應變全曲線本構模型的適用性,圖4給出了本構模型與實測曲線的比較.由圖4可見,應力-應變全曲線本構模型計算結果與實測結果吻合較好,將此模型應用于分析服役結構剩余承載力、變形性能以及非線性有限元模擬是可行的.

2.4 彈性模量

采用反復加載、卸載的方式對不同鋼筋銹蝕損傷混凝土彈性模量進行測試,結果如圖5所示.

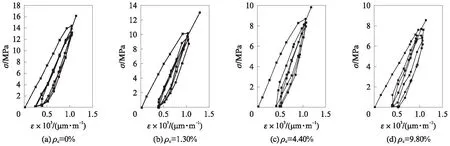
圖5 鋼筋銹蝕損傷混凝土彈性模量測試結果Fig.5 Elastic modulus test results of concretes damaged by rebar corrosion

由圖5可見,由于鋼筋銹蝕損傷混凝土的非彈性性質,每次卸載至零時,變形不能完全恢復,存在殘余應變,且隨著鋼筋實測平均銹蝕率的增加,殘余應變增大.當荷載重復3次后,不同銹蝕損傷混凝土的應變基本趨于穩定,應力-應變曲線接近于直線.取最后一次加載的應力-應變全曲線上應力σ=0.4σ0,c處割線的斜率作為混凝土彈性模量的取值[18],得到銹蝕損傷混凝土彈性模量Ec,c與鋼筋實測平均銹蝕率的關系：

Ec,c=21.604-1.3364ρc,ρc≤10%

(9)

式(9)的擬合相關系數R2=0.9033,擬合結果較好,用其預測氯鹽環境下鋼筋銹蝕損傷混凝土的彈性模量是可行的.

3 結論

(1)鋼筋銹蝕損傷混凝土試件的破壞多為微柱失穩破壞,大致平行于受力方向的銹脹裂縫是主要的破裂面.

(2)鋼筋銹蝕損傷混凝土實測應力-應變曲線與未銹蝕損傷混凝土相似.但是,隨著鋼筋銹蝕率的增加,應力-應變全曲線上升段的斜率逐漸減小,峰值應變增大.當曲線進入下降段后,鋼筋銹蝕率越大的試件,曲線下降段坡度相對越陡,脆性越明顯.

(3)鋼筋銹蝕損傷試件的峰值應力均低于未銹蝕損傷試件,峰值應變、極限應變隨著鋼筋銹蝕率的增加而增大,彈性模量隨著鋼筋銹蝕率的增加而減小.

(4)所建立的鋼筋銹蝕損傷混凝土應力-應變本構模型計算值與實測值吻合較好,可為氯鹽環境下服役鋼筋混凝土結構承載力、變形性能以及非線性有限元分析提供理論依據.