基于多任務協同的粒子群聚類優化算法

顏志鵬

(廣東工業大學計算機學院，廣州 510006)

0 引言

多任務學習(Multi-Task Learning)[1-2]是機器學習，特別是遷移學習中的一個子領域。多任務優化(Multi-Task Optimization)[3-5]應用多任務學習優化，以研究如何有效地同時解決多個優化問題。在多任務學習中，多個相關學習任務使用(部分)共享的模型表示并同時進行訓練。子問題之間也是相互關聯的，通過一些共享因素實現知識遷移從而有效促進單個任務的學習效率和泛化能力。

多任務優化和多目標優化[6-7]之間有相似的地方，但存在根本性的差異。多任務優化的目的是利用種群間個體在多個不同任務之間同時搜索各個目標值對應的最優值，利用潛在的遺傳互補性實現互相之間的遷移學習；多目標優化則試圖解決同一個任務下競爭目標之間的沖突，尋找帕累托前沿上所有的解[8]。如圖1的最小值優化問題，在多目標優化中，P2、P3、P4和P5組成了帕累托前沿，它們被認為是當前解集合中互不支配的最優解；而在多任務進化中，P1、P2、P5和P6組成了最優解，因為這些解都各自有一個目標值達到了最小值。

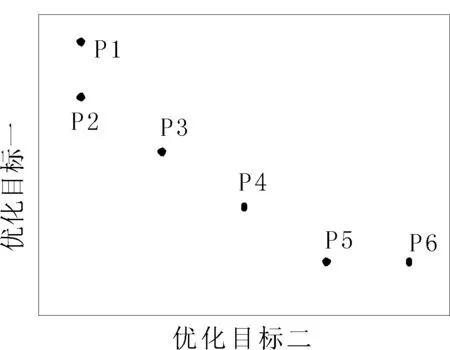
圖1 動態演示程序界面

多任務優化最早用于進化算法中的是多任務進化算法(Evolutionary Multi-Tasking)[9]，它將多任務學習的方法結合進化算法來解決各類優化問題。Gupta等人[9]提出了多因子進化算法MFEA(Multi-Factorial Evolution Algorithm)，在測試了多因子進化算法效果后驗證了多因子進化算法的有效性，證明新算法比單一目標優化更快收斂，更容易找到全局最優值。多因子進化后來得到了發展，不斷有學者改進算法，也衍生出了更多新算法。Gupta等人[10]又將多因子進化算法中單任務只有單個目標拓展到每個任務具有多個目標。Liaw和Ting[11]模仿了生物共生關系為進化算法提出了一個通用的框架，并表明其性能可能比多因子進化算法更好。Cheng等人[12]提出一種多任務協同進化算法(Co-Evolutionary Multi-Tasking)。多任務優化算法可以同時優化多個目標，這點和協同進化算法類似。

聚類通過對沒有標簽的數據劃分為若干相似對象組成的多個簇或類，使得同一類中對象間的相似度最大化，不同類中對象間的相似度最小化。有很多學者提出了基于進化算法進行的聚類，它們大多需要根據一個目標函數進行優化，包括一些經典的聚類內部指標。多目標優化也被應用于聚類問題，例如基于2個目標優化的MOCK(Multi-Objective Clustering with Automatic K-determination)算法[13-14]和基于多目標進化算法的多距離度量聚類[15]。但多目標聚類優化算法為找到帕累托前沿的所有解使用的優化目標往往需要互為沖突，找到的解個數越多，對優質解的篩選難度也越大。多任務學習可以將對不同指標的優化視作不同的任務，分別找到各個任務下最優個體并用專家知識找出最適合數據集的那個聚類指標，對結果的篩選比起基于多目標的方法更容易。

本文針對基于優化算法的聚類和其指標選擇問題以自動聚類粒子群優化ACPSO(Automatic Clustering Approach Based on PSO)[16]為基礎算法，提出了基于多任務協同的粒子群聚類優化算法。算法通過對多個聚類指標優化任務的學習，可以一次性得到多個指標的優化結果。實驗分析發現采用多任務協同優化的方法，可以有效地得到更優的聚類結果。

1 背景

1.1 粒子群算法

粒子群優化(Particle Swarm Optimization，PSO)算法[17-18]是一種模擬鳥群的演化算法，通過記錄種群中每一個粒子經過的歷史最優位置和當前位置來探索全局最優解。本文算法使用的是局部鄰域粒子群算法，即采用環形拓撲的粒子群結構[19]。粒子在迭代中的更新公式為：

xij(t+1)=xij(t)+vij(t+1)

(1)

vij(t+1)=ωvij+c1r1(pbestij-xij(t)+c2r2(lbestij-xij(t)

(2)

其中xij(i=1，…，m;j=1，…，d)和vij(i=1，…，m;j=1，…，d)分別對應粒子的位置和速度，m為種群中的粒子個數，d為數據維度，t為算法迭代次數，t從0開始算法逐次對整個粒子群的速度和位置向量進行迭代優化，r1和r2是0到1之間的隨機數。pbesti為粒子i自身的歷史最優位置，lbesti為粒子i與其鄰近的粒子組成的區域局部最優位置。在頭尾相連的環形拓撲結構的粒子群中，局部區域由該粒子和其前后相鄰的2個粒子組成。w為慣性系數控制粒子位置更新時pbest和lbest的權重。較大的慣性系數有利于全局搜索，而較小的慣性系數一個有利局部搜索，c1和c2為加速常數，分別控制粒子朝全局最優和局部最優收斂的速度。粒子群算法可以用作聚類，如文獻[20]提出的使用量子行為粒子群的動態聚類算法。

1.2 聚類評價指標

聚類集合的優劣評價指標，根據是否需要知道真實的樣本分類標簽，分為內部指標和外部指標。通過對數據分布的進一步研究，人們提出了一些量度數據分布特點的指標，用于聚類算法對聚類集合的優劣評價。

1.2.1 聚類內部指標

內部指標通常用于評估聚類質量或者簇劃分的效果，可以用作優化算法聚類中的目標函數。本文中使用的內部指標包括分析簇劃分提出的較低計算復雜度的CH(Calinski-Harabasz)指標[21]，研究模糊聚類算法提出的Dunn指標[22]，以及聚類有效性的評估方法SIL(Silhouette Statistic)指標[23]。下面給出各個指標的計算公式。

(1)CH指標

(3)

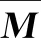
(2)Dunn指標

(4)

其中Ci代表簇i中的樣本數據點組成的集合，D(Ci，Cj)代表不同類別簇i和j間的距離，該值是兩個簇中最靠近的數據點之間的距離，公式表達如下：

(5)

δ(Cl)為簇l的兩個最遠距離點間的距離：

(6)

Dunn指標對數據噪聲比較敏感，數值越大傾向于聚類效果越好。

(3)SIL指標

(7)

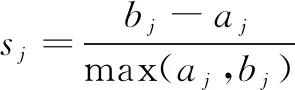
(8)

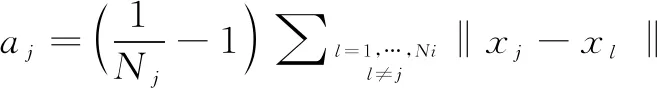
(9)

(10)

其中sj代表數據點xj的輪廓寬度(Silhouette Width)，數據點x到它所屬簇i的其他數據點的平均距離為aj，x到其他類別數據點的最小距離為bj。

SIL指標為正數或者負數分別表示相應的劃分分別是很好的聚類或者錯誤的聚類。SIL指標在零附近被認為對數據沒有明確區分。SIL指標越大傾向于聚類效果越好。

1.2.2 聚類外部指標

聚類外部指標的計算需要知道真實分類情況，因此往往用于檢驗聚類的實際效果。本文使用聚類外部指標調整蘭德系數ARI(Adjusted Rand Index)[24]作為聚類結果的質量評價。ARI是對Rand提出的聚類評價系數蘭德系數(Rand Index)[25]改進后的指標，使得聚類結果在隨機產生的情況下指標能接近于零。ARI假設隨機模型采用廣義超幾何分布，將數據集N個樣本真實劃分表示為P，根據算法聚類得到的劃分為Q，Xi和Xj為數據集的兩個不同樣本。現在按照這兩個樣本在劃分P和C的分布得到以下4種不同的情形：

(1)Xi和Xj在Q中屬于同一個簇，同時它們在P中也屬于同一個類別；

(2)Xi和Xj在Q中屬于同一個簇，但它們在P中屬于不同的類別；

(3)Xi和Xj在Q中屬于不同的簇，但它們在P中屬于同一個類別；

(4)Xi和Xj在Q中屬于不同的簇，它們在P中也不屬于同一個類別。

將以上四種情形成對的樣本數統計并表示為a，b，c和d，可得ARI值：

(11)

ARI為1表示兩個劃分之間的完美一致性，值越小表示它們之間的差異越大。其值也可以為負，表示比隨機得到的分類效果還差。

2 基于多任務協同的粒子群聚類優化

這部分首先描述本文提出的基于多任務協同的ACPSO算法，簡稱MT-CACPSO的粒子編碼及其初始化方法，然后介紹算法聚類時的聚類規則。最后給出算法的多任務協同實現具體流程。

2.1 種群個體的編碼

粒子被編碼為Kmax+Kmax*d維的向量，其中d是樣本點的維度，Kmax是程序定義的聚類樣本簇數的最大值。對于每個粒子的前Kmax個值分別代表后續Kmax個類別中心點的激活閾值。如果該值大于0.5，則對應簇的中心點被激活，相當于該簇被納入聚類的計算，否則不被激活也就是不納入計算。如果該值在優化過程中被修改為大于1或為負數，則重置該值為1或0，如果得到的中心點數量小于設置的最小類別數Kmin，則隨機選取足夠的激活閾值改為大于0.5的隨機值。例如，對于一個維度d為2，最大聚類類別數Kmax為4的個體，前面4個值為激活閾值，第二個位置0.4小于0.5，因此它對應的第二個中心為未激活狀態，以此類推，其他位置的閾值大于0.5從而被激活。因此，這個個體的聚類簇數目為3。

2.2 種群的初始化

每個個體的激活閾值控制著聚類數目，為了讓種群的所有個體不會因隨機性出現偏向，在初始化時會讓個體從最小聚類數Kmin到Kmax均勻分布，因此要控制激活閾值部分的編碼，其余位置則隨機設置為數據各維度所處的范圍內。種群所有個體的初始聚類數K在Kmin到Kmax間呈均勻分布。

2.3 聚類規則

傳統的粒子群優化方式應用于聚類優化時，對于聚類形態非圓形的聚類問題，效果不佳。文獻[16]提出NMP(Nearest Multiple Prototypes)規則用于提升聚類優化中的性能。

首先，每個樣本被分配到最近的簇中，所有被分配到同一個簇的樣本組成了一個候選樣本集。這里，我們把這個簇稱為這些樣本的一個未確定簇。然后，對每一個簇，從候選樣本集中選一個最近的樣本，所有簇的這種最近樣本點合并稱為最近樣本集。最后，在最近樣本集中找到一個樣本，這個樣本離它所在的未確定簇距離是最近樣本集中最小的，就將該樣本分配到它的未確定簇中。不斷重復上述步驟直到所有樣本被分配完畢。相比確定樣本所在類別的傳統方法，NMP是一個動態的過程，更加靈活。

2.4 多任務協同優化

多任務協同優化[12]不僅有多任務的特性，還使用了協同進化讓兩個子群進行交流，而不是對單個種群的優化。本文對算法進行了調整，能夠對更多優化任務進行優化，實驗中的任務數等于聚類優化任務中的指標個數。下文中用集合S表示整個種群，它由被L個任務分割的子種群sk(k=1，2，…，L)組成，即S={s1，s2，…，sL}。

2.4.1 不同優化任務間粒子群的協同進化

在某個優化任務下的粒子群，如果在對其指標優化任務的搜索陷入停滯時則激活該步驟進行跨任務的知識轉移，將粒子的位置偏向另一個被隨機選中的任務的全局最優位置。

假設某個優化任務序號為k，來自該任務的種群內的某個粒子為xi(k)，粒子的個體最優值在經歷γ1次迭代后依然沒找到更優的個體最優值，將對該粒子編碼執行下面的更新操作：

(12)

其中，r1和r2都是[0，1]之間的隨機變量，r3∈[1，L]，且r3≠k，而gbest(r3)表示另一個隨機選中的任務r3的全局最優位置，j=1，2，…，d(d表示粒子編碼的維度個數)。如果粒子更新后得到的優化指標比粒子的歷史最優值更好則更新歷史最優位置，否則不更新。

2.4.2 優化任務內的粒子間雜交

某個種群所代表的優化任務在γ2次迭代后依然沒找到更優的全局最優位置時會隨機從該種群內抽取2個粒子進行雜交，如果雜交得到的后代的適應值大于當前粒子的適應值，則用雜交得到的后代替換父代。雜交的更新公式如下：

(13)

(14)

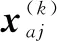
2.5 MT-CACPSO具體流程

本算法包括4個主要步驟，下面以最大化問題為例展示算法流程下：

輸入：數據特征。

輸出：L個指標下對應的聚類結果。

a) 讀入數據集并做歸一化處理，為L個優化指標產生L個個體數為m的粒子群s1，s2，…，sL并初始化；

b) 評估更新每個任務k下每個粒子的pbesti和lbesti(i=1，2，…，m)，k=1，2，…，L;

c) 獲取各個任務的當前的全局最優位置gbestk(迭代次數t←0)，k=1，2，…，L；

e)while(t沒有達到最大迭代次數)t←t+1；

fork=1，2，…，Ldo

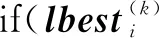
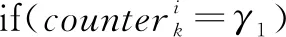
更新完該種群下所有粒子后，獲取任務k的全局最優位置gbestk的適應值fk(t)；

if(fk(t)≤fk(t-1))counterk←counterk+1；

if(counterk=γ2)在該任務粒子群中隨機抽取2個粒子根據公式(13)和(14)進行雜交；counterk=0；

f) 輸出各個任務的全局最優位置作為結果。

在上述步驟中，共有L個粒子種群，分別對應前文提到的L個內部聚類指標。當種群內的粒子陷入停滯時將使用公式(12)更新粒子位置實現種群間的協同進化。判斷粒子是否停滯需要先設定一個系統參數γ1，當某個粒子經歷了γ1次迭代后依然無法獲取到更優的適應值才執行該步驟。此外，某個粒子群的全局最優在經歷γ2次迭代后沒有獲得新的全局最優位置將在該粒子群內進行內部的雜交。

3 算法實驗測試

3.1 測試數據集

數據集選用了人工數據和真實數據，表1中Banknotes和Vertebral Column數據集為真實數據集，它們來自UCI 機器學習數據集(http://archive.ics.uci.edu/ml/index.html)。

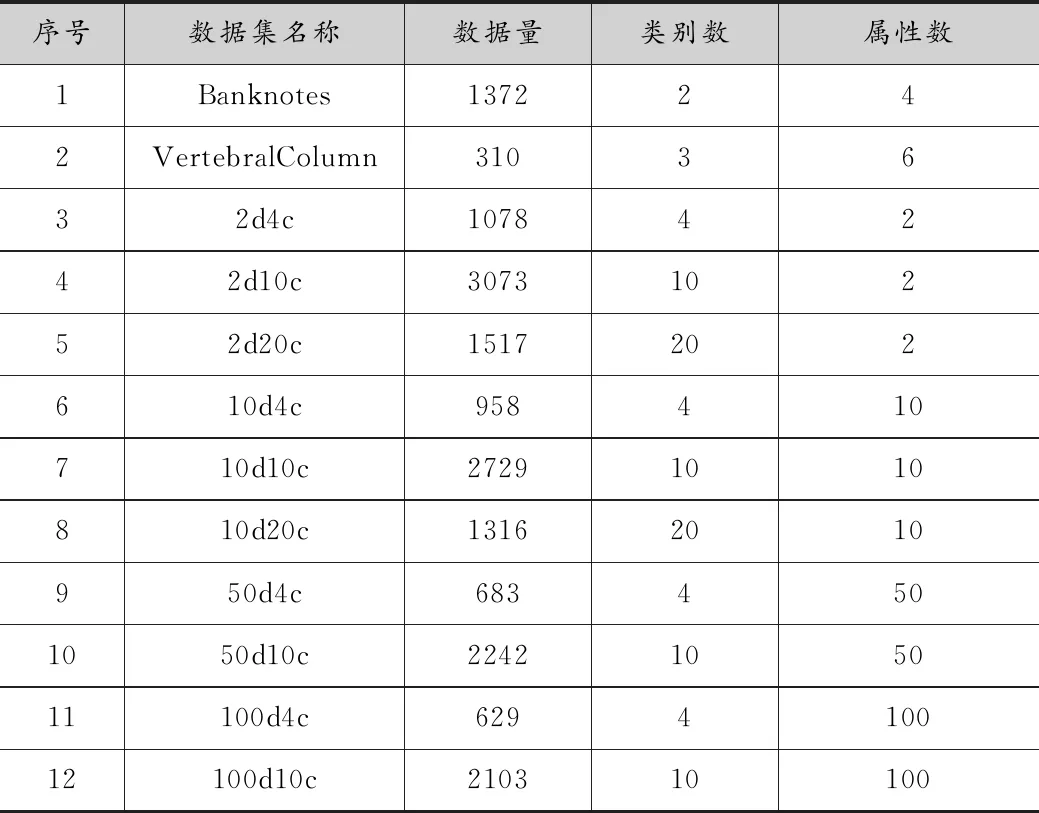
表1 測試的數據集

表1中序號3到12的數據集均為人工數據，它們有著不一樣的形狀的簇，是通過由Handl和Knowles提出的簇生成器[13]得到的，生成器為高維的橢圓形簇，長軸方向上任意分布，2d4c代表這個數據集維度為2，類別數為4。

3.2 參數設置

本實驗比較了3種聚類算法。其中ACPSO是單任務算法，實驗中分別對其采用了不同的聚類內部指標作為優化目標進行測試。ACPSO的種群規模為40，本文提出的MT-CACPSO同時優化多個內部指標任務，每個任務的種群規模為40。最大聚類數Kmax為30，最小聚類數Kmin為2。慣性系數w為0.75，加速度常數c1和c2為2，粒子的最大速度控制在數據范圍的20%內。系統參數γ1=γ2=15。

實驗將MFEA算法用于聚類，即多因子進化聚類算法。MFEA算法的RMP(Random Mating Probability)控制著不同任務之間交流程度，取值范圍為(0，1)，值越大則跨任務間的交流越頻繁[9]。本文實驗中RMP參數取值為0.3。以上3種算法最大迭代次數都為2000次，每個算法都獨立運行10次。

3.3 MT-CACPSO與單任務算法的結果比較

ACPSO是先后選取了不同的3個優化目標(CH、DUNN、SIL)單獨運行而得到的結果，MT-CACPSO是一次運行后得到的3個不同優化任務對應的結果。

表2比較了MT-CACPSO和單任務的ACPSO的實驗結果的內部指標，結果取10次運行的平均值。其中，加粗的結果為同一個內部指標下，兩種算法的優勝結果。多任務MT-CACPSO算法比單任務ACPSO算法獲得更多的優勝解。例如在CH指標上，MT-CACPSO算法在12個實例中有7個實例找到更優的解，而ACPSO算法有6個實例找到了更優的解，其中主要是在維度相對低的數據集上MT-CACPSO表現更優。而在DUNN和SIL指標的優化中，MT-CACPSO算法獲得更多的最優解。在對DUNN指標的優化結果中，MT-CACPSO的優化得到的指標值大都不低于單任務ACPSO，只有2d20c例外，在SIL指標上大部分數據集也優于ACPSO的優化結果，說明MT-CACPSO在這些指標的優化任務上，發生了不同優化任務間的知識遷移，從而得到更好的收斂結果。

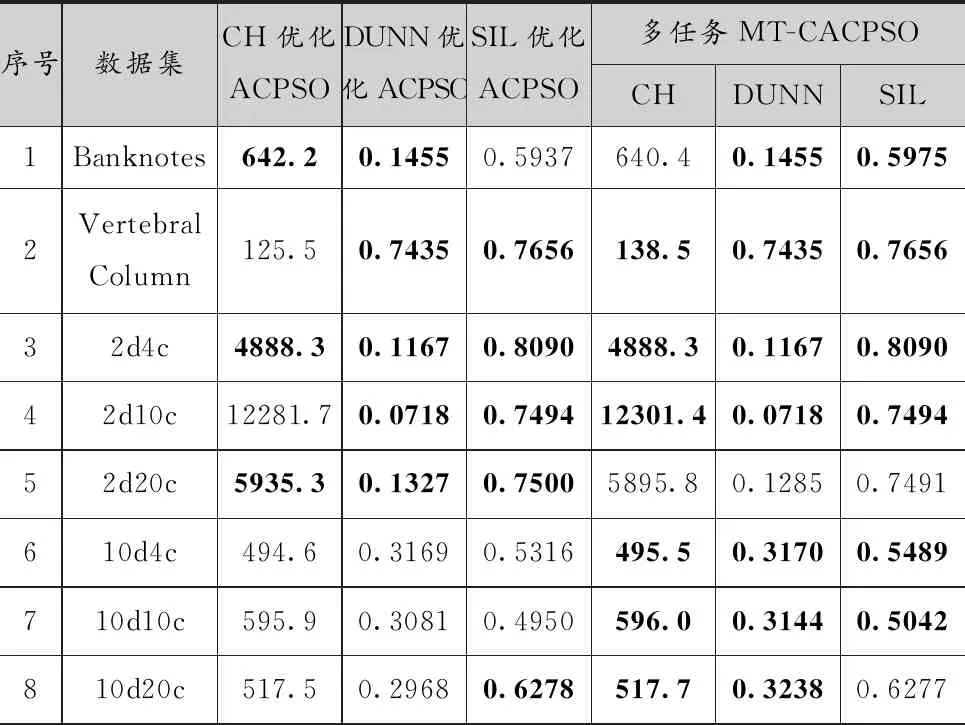
表2 ACPSO與MT-CACPSO運行結果的平均內部指標

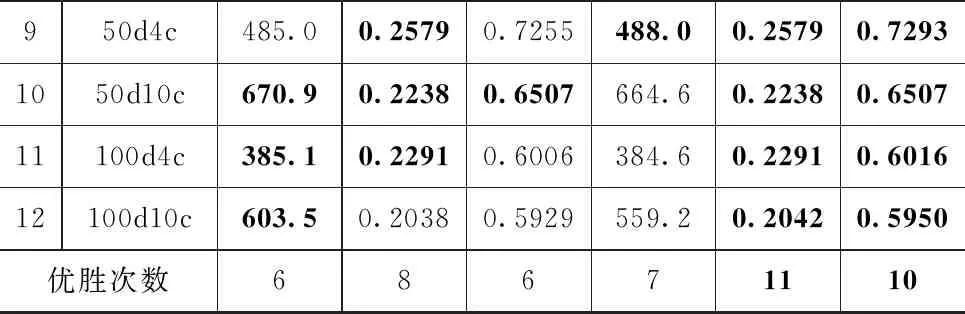
續上表

表3給出了兩種算法的外部聚類指標結果。基于多目標的聚類方法[13-14]中得到的帕累托前沿上所有聚類結果需要進行篩選，類似的，由于使用了多個指標，所以采用多任務的聚類方法也需要引入專家知識對結果進行篩選，而且因為解集個數只等于優化目標個數，所以篩選難度低于基于多目標的方法。通過引入專家知識，我們將最合適該數據集的結果作為最終的聚類結果，表格中加粗的結果表示同一行中最優的ARI值。

對于真實數據集Banknotes和Vertebral Column，MT-CACPSO的CH指標優化任務取得了更好的聚類結果。人工數據集2d4c兩個算法的結果一樣，在DUNN指標優化上獲得了最優結果。其余人工數據集中MT-CACPSO有6個更優的聚類結果，ACPSO則是3個，其中2d10c是SIL優化任務獲得了最好的結果，其他數據集則是CH指標優化結果更好。這體現了不同指標優化對于同一個數據集的不同影響。

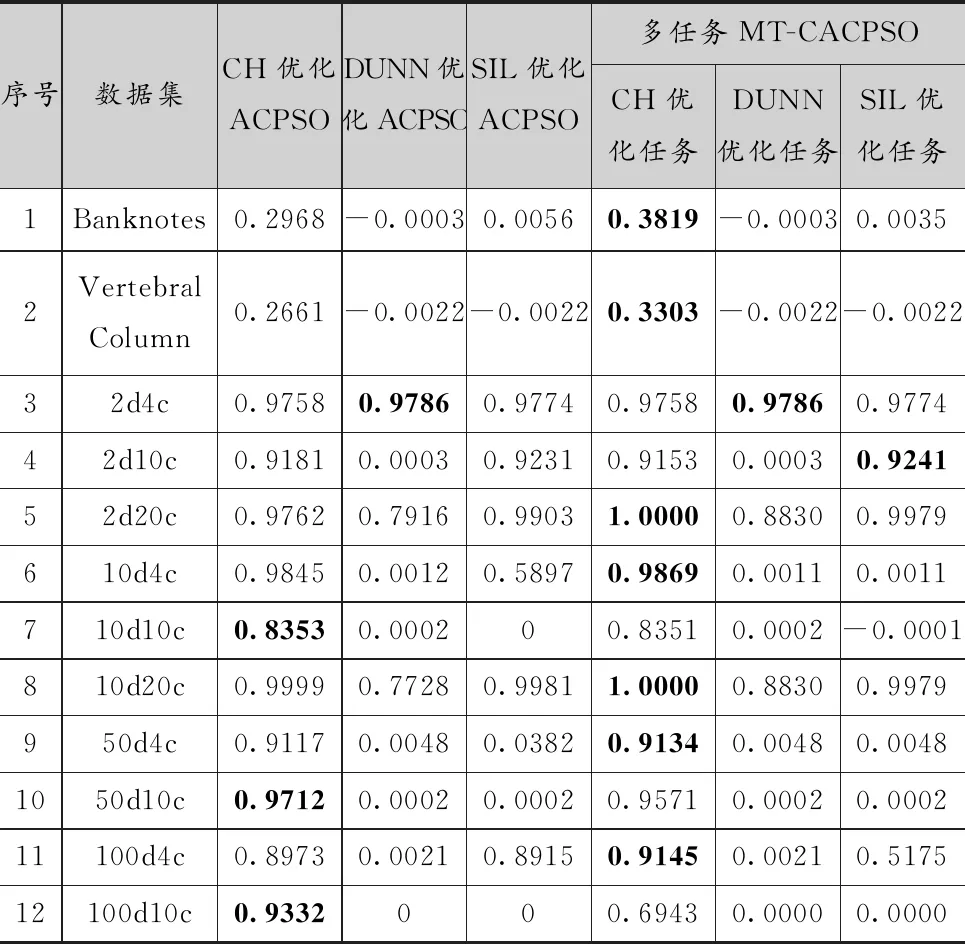
表3 ACPSO與MT-CACPSO運行結果的平均外部指標ARI

3.4 MT-CACPSO與多因子進化聚類算法的結果比較

表4和表5比較了MT-CACPSO和多因子進化聚類(MFEA)算法的實驗結果，每個算法共運行了10遍，結果取十次運行的平均值，兩個多任務聚類算法都是一次運行后得到的3個不同優化任務對應的結果。兩種算法都是基于多任務的聚類算法，該實驗的結果體現了采用協同多任務相對于多因子進化算法的優勢。

表4給出的是兩個算法結果的內部聚類指標，加粗的結果為同一個內部指標下，兩種算法的優勝結果。經過對比，MT-CACPSO在3個指標的優化上都獲得了比多因子進化聚類算法更多的優勝次數。其中，在3個指標優化上MT-CACPSO分別獲得了10、10、11次最優解，而多因子進化聚類算法是3、7、3次。在CH指標優化任務上，MT-CACPSO的結果優越性主要體現于適合使用CH指標優化的超球形或超橢圓形簇人工數據集(序號3到12)，除2d20c外均取得了最優的解。在DUNN指標的優化上MT-CACPSO只有2d20c和10d20c這2個實例沒有取得最優解。SIL指標優化上MT-CACPSO除2d20c外的實例上都獲得了最優解。綜上，使用環形拓撲粒子群的協同多任務算法獲得了更好的收斂結果，是比多因子進化算法更加容易突破局部最優值的多任務優化算法。

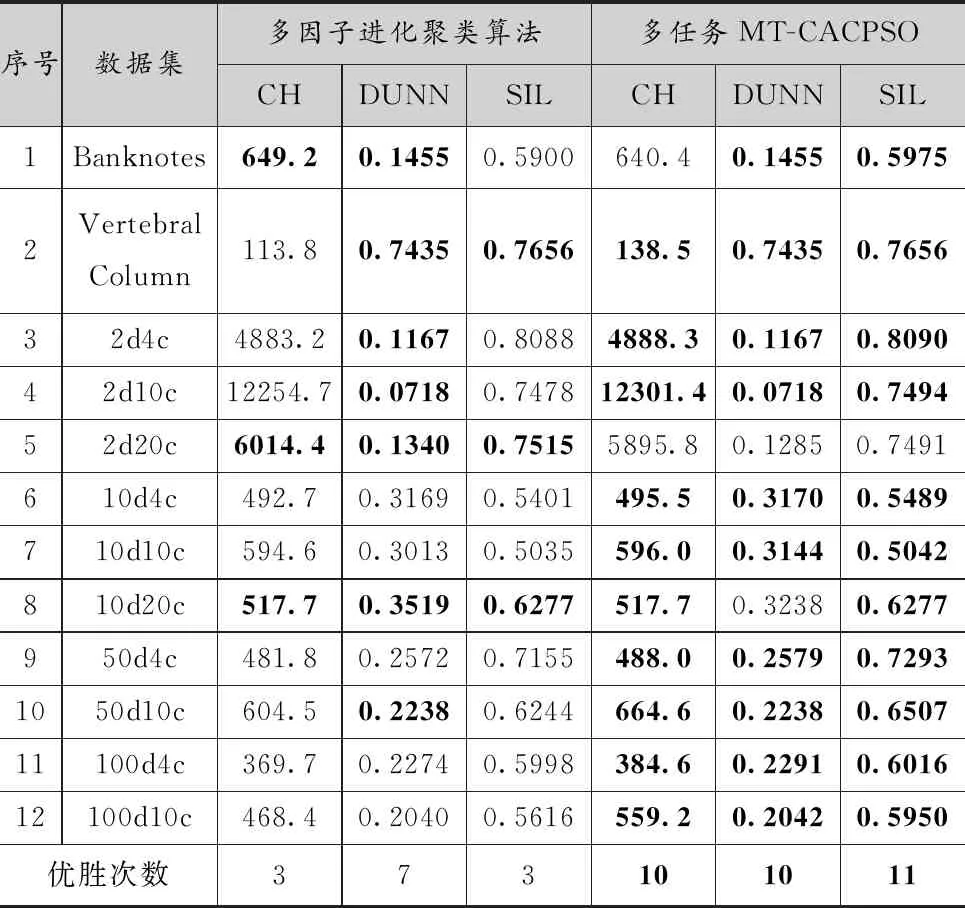
表4 多因子進化聚類算法與MT-CACPSO運行結果的平均內部指標

表5中給出了多因子聚類算法和MT-CACPSO的聚類結果的外部指標，加粗的結果表示同一行中最優的ARI值。真實數據集中，MT-CACPSO聚類結果均取得了最優解。人工數據集中，除2d4c、10d20c和100d4c外，MT-CACPSO均獲得比多因子進化聚類算法更優的聚類結果，其中10d20c則是兩種算法都獲得了完全正確的聚類結果。可以看出，基于多任務協同的聚類算法的聚類效果優于多因子進化聚類算法。

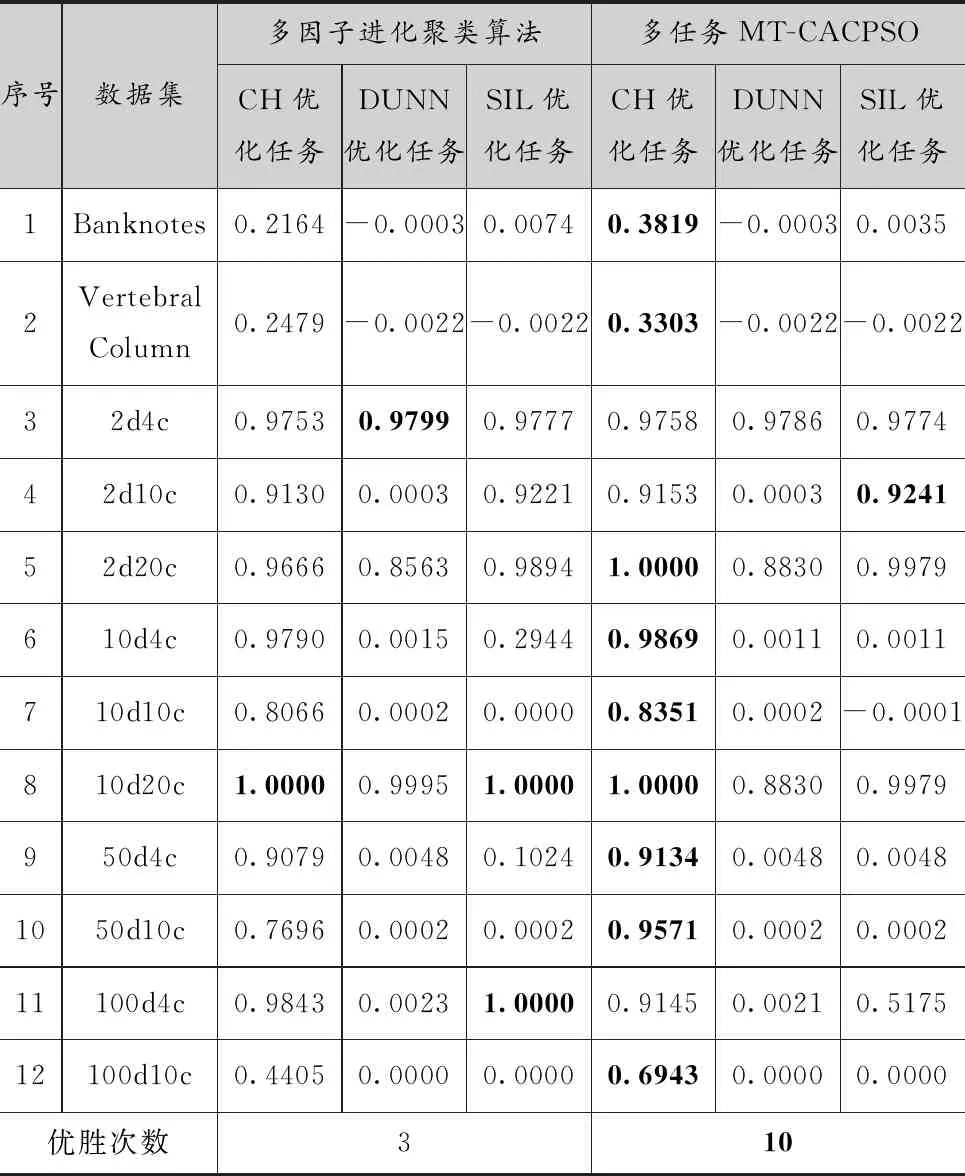
表5 MT-CACPSO與多因子進化聚類算法結果的平均外部ARI值

3.5 算法收斂曲線圖

圖2選取了個別有代表性的數據集，并畫出了3個算法在各個優化指標下的收斂曲線，結果取十次運行的平均值。在2d10c的CH指標優化中，ACPSO在前期的迭代中收斂速度最快，但后續的迭代中MT-CACPSO通過不同任務間的交流實現了局部最小值的突破從而得到了更優的CH指標結果。在10d20c數據集Dunn優化和10d4c數據集SIL優化中，兩種基于多任務的聚類算法都在前期迭代中得到了比ACPSO更優的目標值，而MT-CACPSO的收斂性能又好于多因子聚類算法。

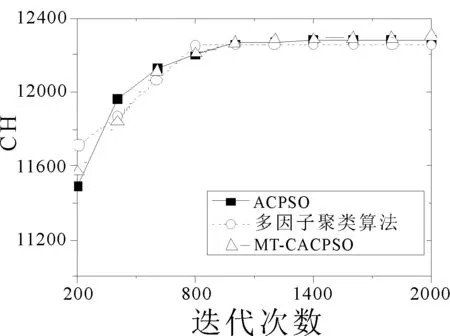
(a) 2d10c CH指標收斂曲線

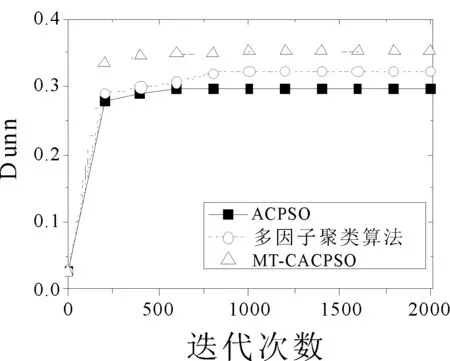
(b) 10d20c Dunn指標收斂曲線

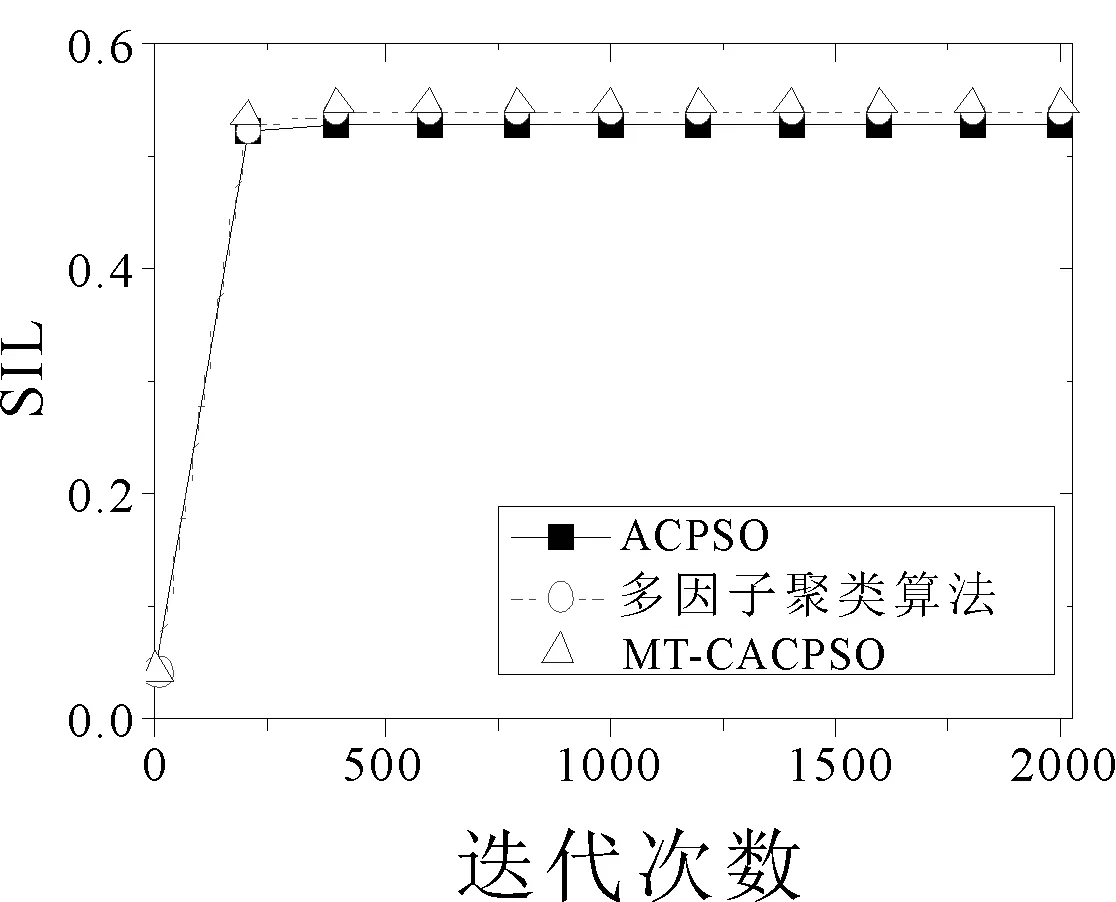
(c) 10d4c SIL指標收斂曲線

4 結語

本文中提出了基于多任務的聚類算法MT-CACPSO，并與單任務的ACPSO和同樣是基于多任務優化的多因子進化聚類算法進行了比較。雖然不同內部指標適用于不同數據集，但基于多任務的聚類算法同時完成對3個不同內部指標的優化后可以用專家知識從中選出一個最優的聚類結果。通過與單任務ACPSO的聚類算法結果對比發現，多任務聚類算法受益于多個指標的不同環境，有機會通過任務間的知識遷移獲得更好的聚類結果。與多因子進化聚類算法的結果對比則說明基于協同多任務進化的聚類算法優于基于多因子進化的聚類算法。