序列分析綜述

張傳斌，陳水標，吳偉堅

(肇慶學院,計算機科學與軟件學院，肇慶 526061)

0 引言

序列分析的應用范圍非常廣泛，如基因和蛋白質的序列分析、信息檢索、健康分析、金融數據分析、交通流預測、天氣預報和網絡安全檢測等。這些都是多學科交叉的領域，具有良好的社會和經濟研究價值，因此序列分析也一直是研究熱點。

我們可以把序列劃分為以下三個類別：

(1)符號序列

符號序列可以是由單個符號組成的簡單有序列表，如DNA序列；也可以是由符號向量組成的有序列表，如用戶每次使用軟件查看新聞的類別序列〈(軍事，新聞，歷史)，(軍事，新聞，新聞)，…，(歷史，新聞，歷史)〉。

(2)時間序列

時間序列是指按一定時間間隔順序排列的符號或數值列表，列表中的值通常是實數或實數向量，如交通流數據、水文和氣溫數據等。在時間序列中，當前元素與之前的元素具有關聯性，蘊含著研究對象的發展趨勢或周期性。

(3)復雜結構序列

復雜結構序列是指序列中的每個元素具有較復雜的結構，如患者的醫療記錄，每個記錄都可能包括姓名、性別、年齡、心電圖、體溫、醫囑和用藥明細等數據。

中國管理科學研究院研究員吳興杰從中美貿易戰的背景切入，以《基于中美貿易戰的鄉村振興戰略的思想創新》為題，重點對鄉村振興戰略的思想創新進行了研究，提出：鄉村振興戰略的重點和難點在中西部落后鄉村，東部特別是沿海鄉村要實現從富起來到強起來再到美起來。鄉村振興戰略要從政治訴求轉化為發展的內在邏輯進而落地的關鍵是思想的創新，即哲學創新。規避鄉村振興“上熱下冷→外熱內冷→表熱實冷”的關鍵，是解決誰來干和怎么干這兩大核心問題，防止樣板化、錯位化與非農化而偏離其正軌。

1 序列分析任務類型

序列分析的任務主要有分類和預測。符號序列主要以分類操作為主，如對新蛋白質進行歸類，對新聞軟件的用戶進行分類等。預測任務常用于時間序列的分析，如預測交通流的趨勢、股票走勢預測，天氣預報等，時間序列也可通過分類進行分析，如對長期的全球氣溫數據進行分析，判斷那段時間是否屬于厄爾尼諾現象頻發的異常氣候時期。

分類任務主要有三大技術難點：①較難從序列中提取出合適的特征值，而對于絕大部分分類算法來說，特征值的好壞直接影響分類器的性能；②即使能從序列中提取出特征，其特征空間也是高維空間，計算難度很大；③某些序列甚至無法提取明確的特征值。

對時間序列的預測任務中，同樣也面臨著特征提取困難的挑戰，而且序列的前后元素存在耦合現象，特征的次序也會對預測效果產生較大影響。

2 序列分類方法

2.1 基于特征的分類

這種方法將序列轉換成特征向量，再使用各種分類算法進行分類。K元語義模型(K-Gram)是其中一種提取序列特征的方法。一般是指定一個K元短序列的集合，將源序列表示為短序列出現和缺失情況的向量，或者短序列出現頻率的向量，然后再使用傳統的分類方法進行處理[1-3]。此外還有基于模式的特征選擇方法，通過這種方法獲取滿足以下三個條件的特征：①在某個類中常見；②與該類別高度相關；③僅出現在該類別中。通過上述方式提取特征后，就可以進行分類，如使用樸素貝葉斯算法進行處理[4-5]。以上的方法通常是針對序列的局部進行特征提取，Aggarwal等人[6]通過小波分析，將序列分解為不同頻率的子波，從近似和細節兩個方面提取特征值，再通過K近鄰算法進行分類。

2.2 基于距離的分類

這種方法通過計算序列間的距離來進行分類，序列間的相似程度可以通過一系列距離函數來衡量，然后使用K近鄰算法、支持向量機等算法，根據序列間的距離進行分類操作[7-10]。

歐幾里德距離是最為常用的距離計算方法。假設有兩個長度為L的序列S和S′，則兩者間的距離可通過以下公式進行計算：

在蛋白質和基因測序等應用中，不同序列的長度可能不同，動態時間規整(Dynamic Time Warping，DTW)距離[11]可用于衡量長度不同的序列的相似程度。

其主要思想是盡可能按順序對序列中較相似的片段進行比較，但序列中的點不需要進行一一對應，片段間可存在一些間隔點，如圖1所示。此外，還有類似的改進算法[12-14]，通過局部對齊的方式計算兩個序列間的距離。

核函數可將序列映射到超平面，在超平面中使用支持向量機進行切分，能有效地提升長序列的分類性能。其中K-譜核(K-spectrum kernel)是應用最為廣泛的核函數[15]。Lodhi等人[16]提出一種字符串核(string kernel)方法處理文本分類，給定一個長度均為K的子序列的集合，將源序列轉換成子序列權重值的特征向量。K-譜核有許多改進算法，提升了K-譜核函數的計算效率，并對不匹配的權值也進行了適當處理[10，17]。此外還有其他類型的核函數[18-19]，并在各種符號序列分類應用中取得了不錯的效果。

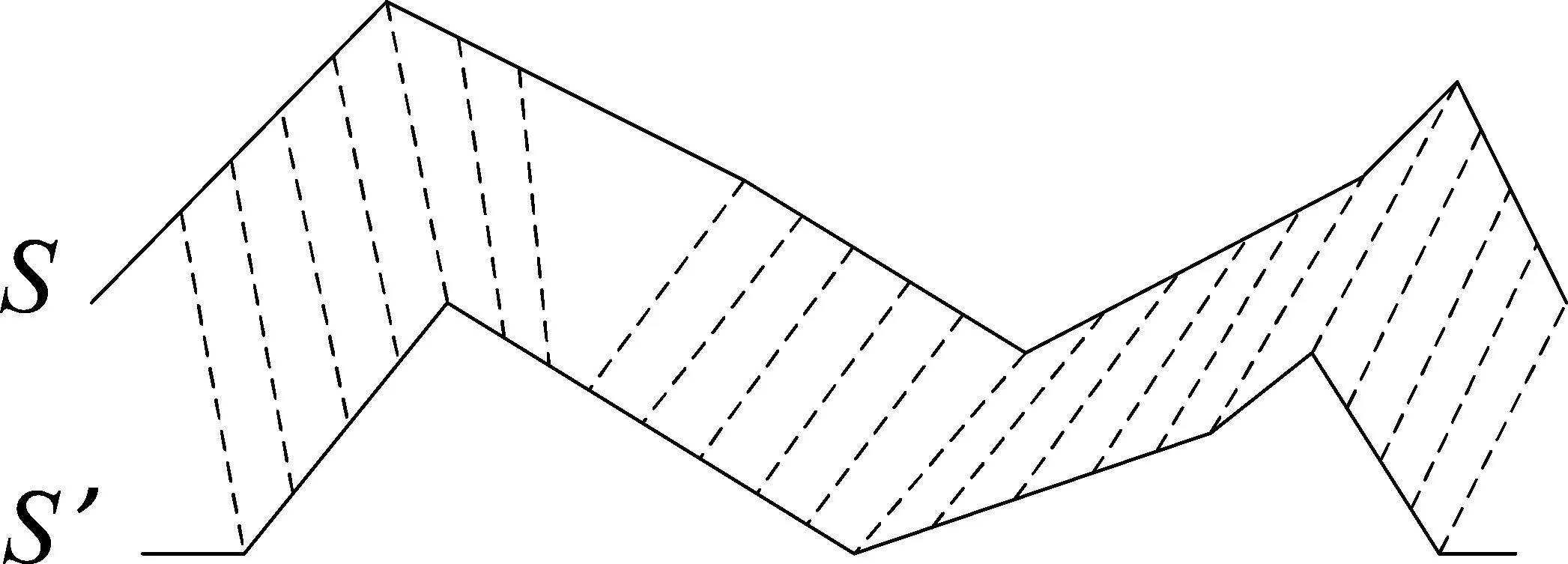
圖1 動態時間規整距離的計算方式

2.3 基于模型的分類

樸素貝葉斯模型[20]原理簡單、適用性強，被廣泛應用于文本分類[21]及其他符號序列的分類任務，如基因和蛋白質測序[22]。根據應用場景的特點，許多改良的樸素貝葉斯模型也取得了不錯的效果，文獻[25]在訓練樸素貝葉斯模型時，使用期望最大化過程去優化參數。樸素貝葉斯模型通常要求每條序列是相互獨立的，而馬爾可夫鏈模型或隱馬爾可夫鏈模型可用于處理存在相互依賴關系的序列。Yakhnenko等人[23]使用K階馬爾科夫鏈模型處理蛋白質分類和文本序列。Srivastava等人[24]使用隱馬爾可夫鏈模型處理生物序列，此文章的模型通過嵌入、匹配和刪除三個狀態進行學習，并會為每個訓練集中的各個類分別進行學習，在對新序列進行分類時，會使用所有訓練得到模型進行測試，將新序列歸類為可能性最高的一類。Kalpakis等人[26]使用求和自回歸平均模型(Autoregressive Integrated Moving Average Model，ARIMA)來描述時間序列，并通過計算兩個序列的線性預測編碼倒譜(Linear Predictive Coding Cepstrum)之間的歐幾里德距離來量化相似程度。

3 序列預測方法

時間序列一般具有趨勢性和周期性，如某條河流的水文數據、道路的交通流數據、某地的氣溫數據。從宏觀角度看，我們可以觀測到這些數據的趨勢或者周期波動。此外，序列也可能是服從某種概率分布隨機產生的，如拋擲硬幣的正反面結果的序列、粒子進行布朗運動的位置序列，我們也可以通過統計方法分析序列蘊含的規律。另外，由于現實世界存在許多偶然因素，數據測量也會引入誤差，時間序列也包含不確定性和噪聲。

3.1 傳統的時間序列模型

傳統的時間序列模型將序列分為平穩時間序列和非平穩時間序列兩類。平穩時間序列是指序列通過隨機過程生成，而且其統計規律保持不變，即滿足均值和方差不變，任意兩個時間間隔的協方差與當前時間無關。針對這類時間序列的模型有自回歸模型(Auto Regressive，AR)、移動平均模型(Moving Average，MA)、自回歸移動平均模型(Auto Regressive Moving Average，ARMA)[27-28]。

非平穩時間序列是指序列具有時變均值，現實場景中的時間序列大多是非平穩的，如股價變化、移動軌跡等[27]。然而序列元素之間的差值可能具備平穩性，如果一個時間序列{Xt}經過d次差分得到的序列是一個平穩的ARMA過程，則{Xt可通過自回歸積分滑動平均模型(Autoregressive Integrated Moving Average Model，ARIMA)進行描述。一個具體的應用例子是Kumar等人使用ARIMA預測交通噪聲的變化情況[30]。

“Box-Jenkins”方法[31]是一種求解上述四個模型參數的通用方法，其步驟如下：

(1)根據序列的圖形大致判斷序列的平穩性，也可以通過分段計算序列的均值和方差進行判斷，更為嚴謹的判斷方法為增廣迪基-福勒檢驗(Augmented Dickey-Fuller test)[32]。如果序列為非平穩的，則先對序列進行d次差分運算，轉化為平穩時間序列。

(2)求第(1)步獲得的平穩序列的偏自相關函數(Partial Auto-Correlation Function，PACF)和自相關函數(Auto-Correlation Function，ACF)，根據所求圖形確定p或q的值。

(3)根據前兩步的計算結果選取合適的模型，利用序列數據對模型進行擬合，計算出剩余的參數φ，θ，c。此步驟可通過最大似然估計[27]和EM算法(Expectation Maximization Algorithm)求解[33]。

3.2 支持向量機

支持向量機(Support Vector Machine，SVM)是一種基于統計學習理論的算法，在處理高維度和非線性問題時具有強大能力。支持向量機被廣泛運用于經濟數據的預測[34-37]，這些文章的主要思想時將時間序列被映射到超平面，然后在超平面中使用最小二乘支持向量機，建立回歸方程，實現預測。Ip等人[38]將最小二乘支持向量機用于空氣污染狀況的預測，用于測試的時間序列中的元素是由污染水平、風向、溫度、濕度等因素組成的向量，取得了良好的預測效果。Mellit等人[39]使用最小二乘支持向量機預測氣候狀況，文章中的時間序列包含光照、氣溫、相對濕度、風速、風向和氣壓等因素，支持向量機在測試集中的效果最優。

3.3 神經網絡與深度學習

神經網絡(Neural Network，NN)也稱人工神經網絡，是參考生物的神經結構設計的一種網絡模型[40]。利用大量數據對有足夠數量神經元的神經網絡進行訓練，能讓神經網絡學習到數據中隱含的統計規律，相當于建立了一個非常復雜的函數，從而實現對新事件的預測。Abhishek等人[41]使用反向傳播神經網絡(Back-Propagation Neural Network)實現降水值的預測。Mellit等人[42]利用神經網絡提前一天預測日照情況，幫助光伏發電廠進行能源調度。Yang等人[43]和Thomas等人[44]在病毒研究時，通過神經網絡預測蛋白酶的切割位置，為藥物研制提供精準靶點，提高疾病的治療效果。

深度學習(Deep Learning)脫胎于神經網絡，通過增加大量隱層，并逐層進行特征變換的方式獲取數據更深層的特征，而且克服了神經網絡容易過擬合、調參困難和訓練速度較慢等問題[45]。

深度學習是當前非常熱門的人工智能研究領域之一，在圖像處理、模式識別等領域取得了豐碩成果。AlphaGo利用大量的人類對弈數據和自我對弈數據進行深度學習訓練，在與人類對弈時同時使用四個策略網絡進行評估和預測，擊敗了人類最頂級的棋手[46]。Hinton等人[47]總結了深度學習在語音識別方面的成果，目前已經有大量用于商用的語音識別系統。Yu等人[48]提出了一個時序正則化矩陣分解(Temporal Regularized Matrix Factorization，TRMF)框架處理高維時間序列問題。Lai等人[49]提出了利用深度學習對長短時間模式進行建模，為處理各類多元時間序列數據提供了一個通用框架。

4 結語

本文介紹了序列分析任務類型和序列的分類預測方法，并闡述了分類和預測方法中所常用的各種技術如小波分析、支持向量機、人工神經網絡等。這些技術方法解決了實際工作中的一些相關問題，并具有一定的實際意義和應用價值。