基于規則的柔性作業車間機床與AGV聯合調度優化*

郭沛佩 付建林 江海凡 王 坤

(①西南交通大學先進設計與制造技術研究所，四川 成都610031； ②成都運達科技股份有限公司，四川 成都610031))

自動導引車系統(automatic guided vehicle system，AGVS)作為一種靈活高效的物流系統在制造、倉儲配送等領域有著廣泛的應用，目前柔性作業車間越來越多地采用AGV進行物料輸送，柔性作業車間集成AGV聯合調度問題應運而生。國內外對傳統作業車間AGV調度研究已較多，但這些研究都假定每個工件的工藝路線是確定的[1]，而在柔性作業車間中，由于每個工件的每道工序都有不同機床可供選擇，且在不同機床上的加工時間不同，工件的可變工藝路徑又導致AGV路徑選擇不同，這些不同組合會有不同結果，也更符合現代多品種小批量的生產方式，因此優化柔性作業車間機床和多AGV的集成調度具有重要意義[2]。

集成調度問題是NP難問題，最先考慮了諸如數學建模或基于圖形的算法之類的集中方法，盡管這些方法能找到最佳解決方案，但它們只能應用于小型場景[3]。國內外學者開展了一系列圍繞柔性作業車間調度的研究，元啟發式智能算法提供了有效的途徑[4]，包括遺傳算法[5]、粒子群優化算法[6]和模擬退火[7]等，但隨著求解問題復雜度上升，這些算法的解空間呈指數爆炸性增長，計算時間長，且容易出現早熟與陷入局部最優問題。除此之外，啟發式規則調度方法由于其易于實現，計算效率高、有健壯的魯棒性，被廣泛應用于車間調度問題。從實際生產系統的復雜性、規模性和可操作性角度考慮，啟發式調度規則仍然是目前最可行和有效的求解方法[8]。柔性車間中，不同資源有不同調度規則，可采用單一規則或組合規則方式解決實際問題，楊小佳[9]等人為比較柔性裝配作業車間中兩類動態調度策略，采用了優先度規則方法研究不同擾動下的完全反應式調度，得出采用組合規則性能更優結論。Doh Hyoung Ho[10]等人則比較了不同組合規則，證明采用恰當規則組合可優化車間性能，朱偉[11]采用規則導向思想選擇更合適的規則組合解決了柔性作業車間多目標集成優化問題，但他們所解決的調度問題針對的都是車間中機床與作業排序聯合調度問題，基于規則的機床與AGV聯合調度研究較少；Jens Heger[12]采用不同規則組合解決了對作業排序、機床和AGV這3類問題的調度，但并未考慮系統中所需配置AGV數量對調度結果的影響；文獻[13]以最小化平均延遲時間為目標采用神經網絡預測不同AGV和機器利用率下車間所適用的3類規則組合，但并未考慮不同任務水平對求解模型性能影響。

本文采用離散事件建模仿真方法搭建了一個柔性作業車間仿真模型研究機床與AGV聯合調度問題，以最小化平均流動時間、完工時間、合適AGV平均利用率與完工數量為指標比較了3種工件路由規則與3種AGV調度規則的組合影響，確定出最優規則組合與所需配置的AGV數量，并在確定的最優規則組合下尋找最優的任務到達模式與AGV數量，得到柔性生產車間性能最優時的最佳規則組合、最佳AGV數量和最佳任務達到模式。

1 問題描述

1.1 柔性作業車間聯合調度問題描述

柔性作業車間機床與AGV聯合調度問題一般可描述為工件集J={J1,J2,…,Jn}在機床集M={M1,M2,…,Mm}上加工并由AGV集T={T1,T2,…,Tk}實現其搬運的過程。求解該類問題通常需滿足如下假設條件：

(1)初始時刻，所有工件均處于待加工狀態，所有機器均處于空閑狀態。

(2)同一時刻，同一臺機器只能加工1個工件的某道工序。

(3)同一時刻，同一工件只能被一臺機器加工，且不允許中斷正在加工的工序。

(4) 同一工件的工序加工順序固定且不可更改，不同工件的工序間沒有順序約束關系。

(5)同一AGV1次只能運輸一個工件。

車間中每個工件包含系列工序Oij(i為工件號，j為工序號)，每道工序都將在M中的某臺機床上加工，每加工完一道工序都需要T中的某臺AGV搬運至下道工序位置，故柔性作業車間機床與AGV聯合調度問題可看作是每道工序加工與運輸問題的組成

1.2 主要的優先級規則

優先級調度規則方法指按一定的準則對待加工工件、加工設備、運輸設備進行優先級排序，以提供1個合適的解決方案。本文采用不同工件路由規則(一道工序有多臺機床可供選擇時，從中選出一臺機床的操作稱為工件的路由，即調度機床)、AGV調度規則組合的方法研究此問題，并找到最合適的規則組合優化調度。文獻[13]采用了一些常用的工件路由規則，文獻[14]回顧了多種AGV調度規則,這些規則都能有效解決車間調度問題，據此本文所采用的規則如表1所示：

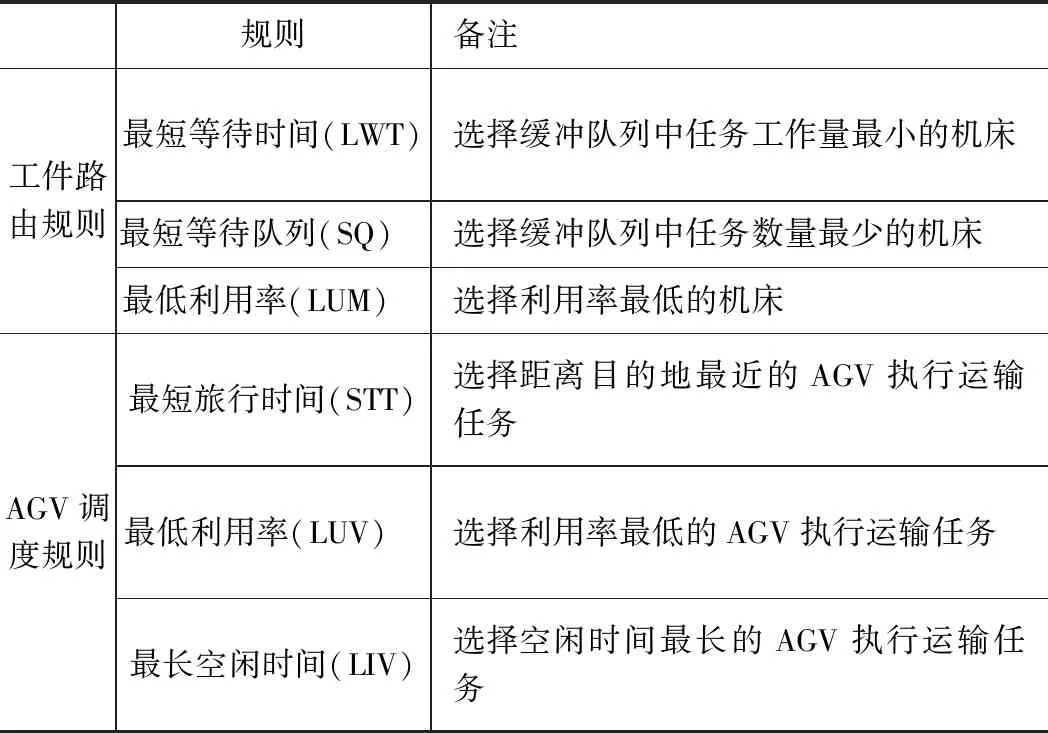
表1 主要的優先級規則

評價不同規則組合時，采用多重性能指標如表2所示。

表2 規則組合及其所需AGV數量的評價指標

1.3 規則組合下的AGV數量配置、任務到達模式問題描述

作為柔性作業車間的主流物料搬運設備，AGV數量將對表2中的評價指標產生較大影響：數量過少將導致搬運任務不能得到及時處理，工件大量堆積在系統中，各指標值過大，AGV過忙，可能造成無論采用何種規則組合同時調度機床與AGV，調度結果都十分不理想，所評價出的規則組合是沒有實際意義的；AGV數量過多，即便不會對評價指標造成過大影響，也將直面資源浪費問題。故需要確定出系統所需配置的AGV最佳數量。考慮到不同規則組合可能對最佳AGV數量造成影響，故其需與規則組合同時評判。

在最優規則組合以及最優AGV數量配置下，系統性能不一定為最優，為進一步提升系統性能，可考慮前兩種條件最優情況下任務到達模式影響，主要包括任務到達頻率和任務投產方式兩方面內容，研究過程中，各影響因素可能相互制約，最后相互確定出各自的最優選擇。

2 驗證實例及建模仿真過程

2.1 實例描述

本研究所設計的柔性作業車間共包含6臺機床M1～M6，每臺機床具備1～2種加工技能，以滿足加工柔性。物料搬運設備采用AGV。加工產品有4類分別為：J1、J2、J3和J4，每類產品包含4道工序，其工藝路線及每道工序可供選擇的機床及其加工時間如表3所示，如處理J1產品的第一道工序O11時可選擇M4、M5兩臺機床，選擇M4時，所需加工時間P11為100 s，選擇M5時，P11為70 s。

車間實際生產時，工件到達時間間隔服從泊松分布，泊松參數λ=140，每類工件待加工數量為250件，采用J1～J4順序生產投產方式，AGV數量待定，企圖在此生產條件下，找到車間性能最優時的規則組合與所需AGV數量，以解決機床與AGV聯合調度問題。

聯合調度問題解決以后，可能存在原本的生產條件不合理的情況，為已找到的最優規則組合匹配一個更合適的生產條件，將進一步提升系統性能。此時規則組合為已知條件，待優化參數為泊松參數λ，AGV數量，投產方式及批量等。

表3 每道工序可供選擇的機床集及加工時間

2.2 離散制造系統建模及仿真

PlantSimulation是一款面向對象的離散事件動態系統仿真軟件，為建模、仿真運行和顯示提供了一種完全面向對象的、圖形化的和集成的工作環境[17]。利用Plant Simulation對設計的柔性作業車間建模及控制過程如下：

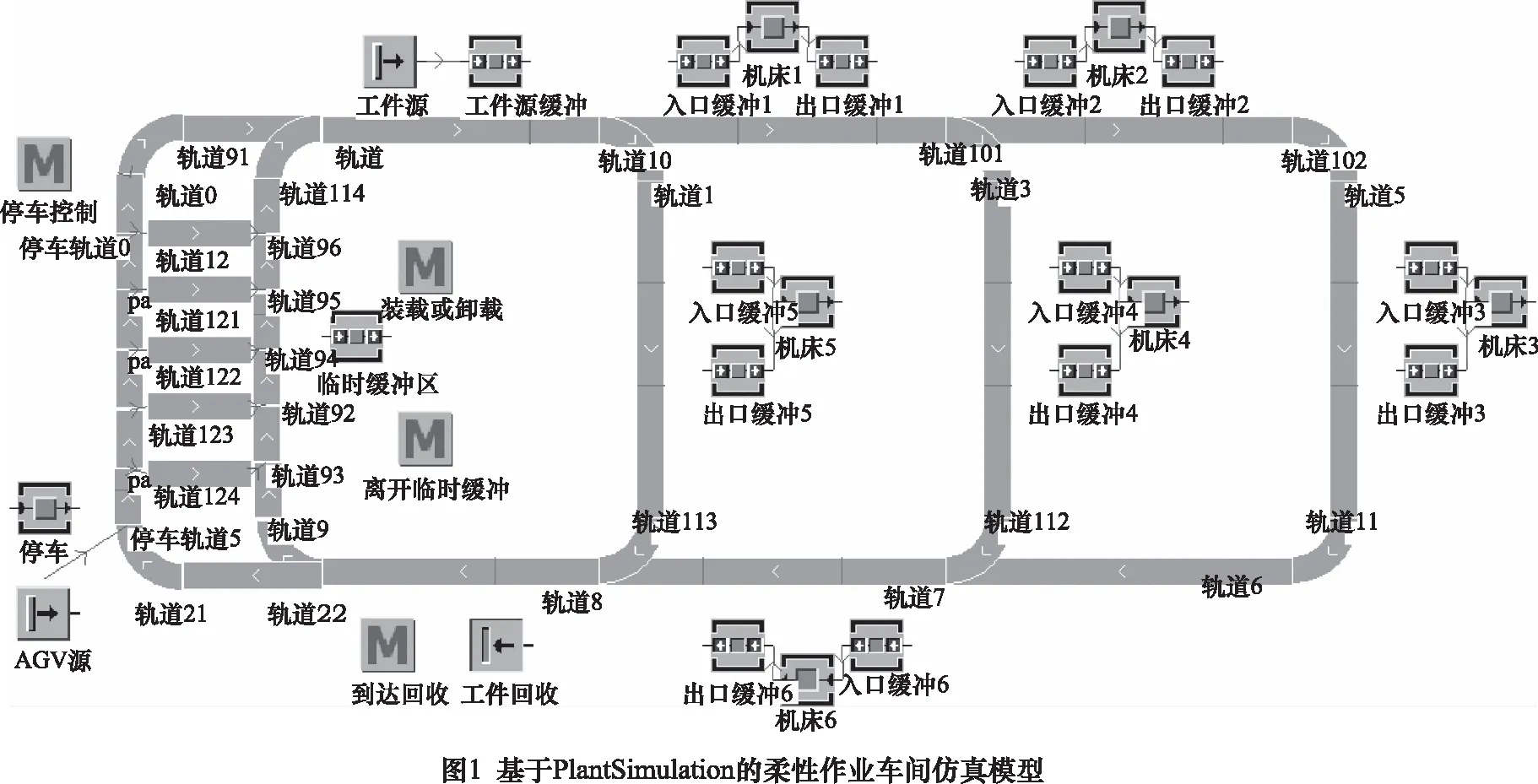
(1)車間布局及建模

利用PlantSimulation對設計的柔性作業車間建模如圖1所示:建立6臺柔性機床，依次命名為M1、M2、M3、M4、M5和M6，每臺機床都有一個入口緩沖BufIn和出口緩沖BufOut,如BufInM1和BufOutM1。生產訂單由jobsource對象產生，產生的四類工件命名為J1、J2、J3和J4。AGV由AGVSource對象產生，其長度為1.5 m，行駛速度為1 m/s，加速度為0.5 m/s2，系統所能容納的AGV最大數量為6，AGV在沒有運輸任務的情況下，將停靠在Parking區域軌道(最左側軌道)上。所有工序加工完成的工件最終將被代表系統出口的Drain對象回收。

(2)仿真過程控制

仿真過程控制包括生產訂單控制、工藝流轉控制、物流運輸任務控制3方面內容。生產訂單由source對象控制，有順序生產和順序循環兩種投產方式，任務到達頻率也在此處設置。工藝流轉控制主要保證工件每加工完一道工序便能讀取到下步工序信息，以便后續加工任務展開。物流運輸任務控制則實現工件在機床與機床之間流轉，流轉的搬運任務由AGV完成。工件在進入系統或加工完一道工序離開sourcebuf、BufOut等出口緩沖時將觸發路由控制程序，按待加工工序讀取該工件的工序表，然后按照給定的路由規則為該工件調度下道工序的加工機床并記錄其加工時間，同時工件在出口緩沖離開事件意味著搬運任務的產生，此時觸發的路由程序還要將工件從當前工序到達下步工序的搬運任務信息實時存儲，這樣上層程序檢測到有待執行搬運任務時，將按照給定的調度規則為其調度空閑AGV，任務一旦被執行，便從任務表中刪除。

3 仿真試驗及結果分析

3.1 最優規則組合及其所需AGV數量分析

本研究主要考慮上文提到的3種路由規則和3種調度規則的組合影響，共有9種規則組合待比較。仿真運行時，利用試驗管理器管理試驗，在同一種規則組合下，AGV數量為1～6，每次試驗重復5次，共進行270次試驗。

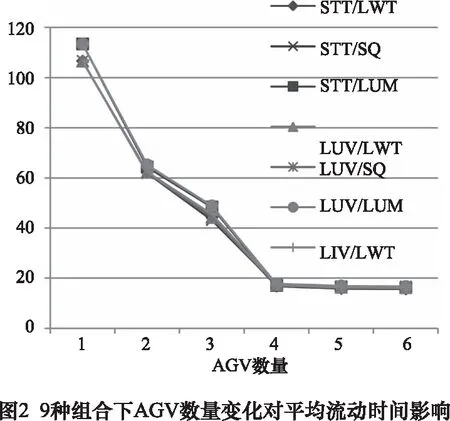
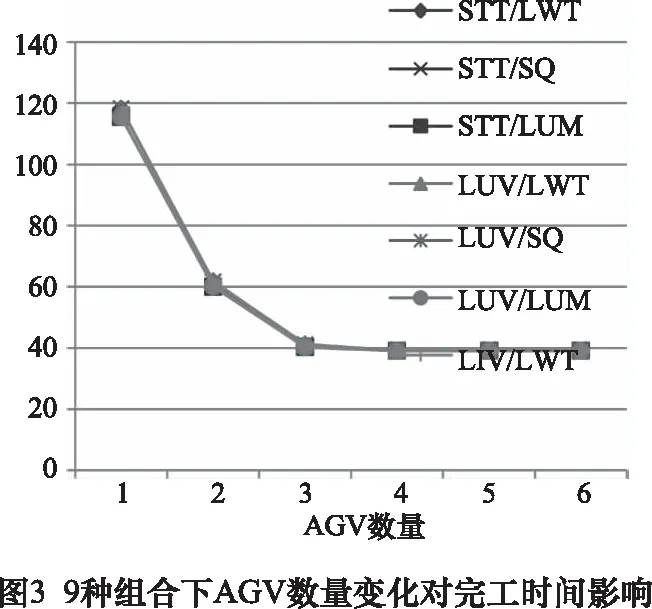
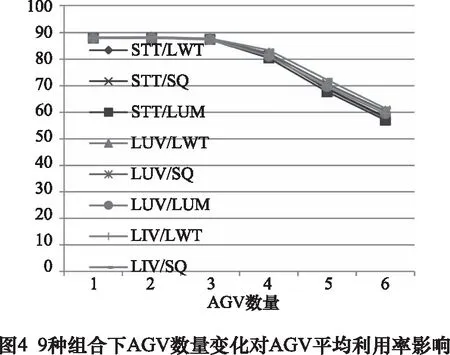
試驗結果分析如下：圖2～4所示為9種規則組合下的3種性能指標變化趨勢圖，在不同規則組合下，各指標走勢相同，但各點數值有差異，該結果表明，采用規則調度方法能解決柔性作業車間中機床與AGV聯合調度問題，且針對同一車間存在一個最優規則組合優化調度結果。

從圖2～4可看出在所有規則組合下系統的性能指標1工件平均流動時間隨AGV數量增加呈逐步下降趨勢，在數量為4時開始趨于穩定。性能指標2完工時間隨AGV數量增加也呈逐步下降趨勢，且在AGV數量為3時穩定，但此時的平均流動時間值遠大于AGV數量為4時的值，故AGV應配置4輛，此時4輛AGV的平均利用率均在81%左右，相比3輛AGV時的88%左右平均利用率，配置4輛AGV時繁忙程度也更合適。綜合比較，該模型在所有規則組合下的小車數量最優值為4。結果表明，在同一任務水平下，采用不同的規則組合不會對所需AGV最佳數量造成太大影響，但會在不同程度上改善系統性能。

在所有規則組合下，AGV數量為4時，系統性能達到穩定，可采用此時的指標值評判規則組合，由于完工時間與AGV平均利用率兩項指標的穩定值在不同規則組合下變化不大，故選擇平均流動時間評判，其結果如圖5所示，可以發現無論何種調度規則下均為路由規則LWT優于LUM，再遠優于SQ。無論何種路由規則情況下，調度規則均為STT最優。最終確定該模型最適用的AGV數量與規則組合為：小車數量為4時的LWT/STT組合。為更直觀體現最優規則組合對平均流動時間影響，定義系統性能提升指數μ，按式(1)計算。

(1)

得到最優規則組合較于其他組合系統性能最大提升6%。

3.2 最優任務到達模式及其所需AGV數量分析

上文所找到的最優規則組合，是在已知生產條件任務到達頻率服從泊松140分布，順序投產下研究的，針對此最優規則組合，可能還將存在更優的任務到達模式，進一步提升系統性能。

(1)任務到達頻率分析

固定規則組合為STT/LWT，變化泊松參數λ值從40～220，AGV數量從1～6，研究最優規則組合下最優的任務到達頻率及所需AGV數量。仍采用試驗管理器管理試驗，每次試驗重復5次，共進行300次試驗，試驗結果分析如下：

如圖6所示，在不同的任務到達時間間隔下，工件的平均流動時間隨AGV數量增加呈不同變化趨勢，具體趨勢分析及取舍結果如表4所示。

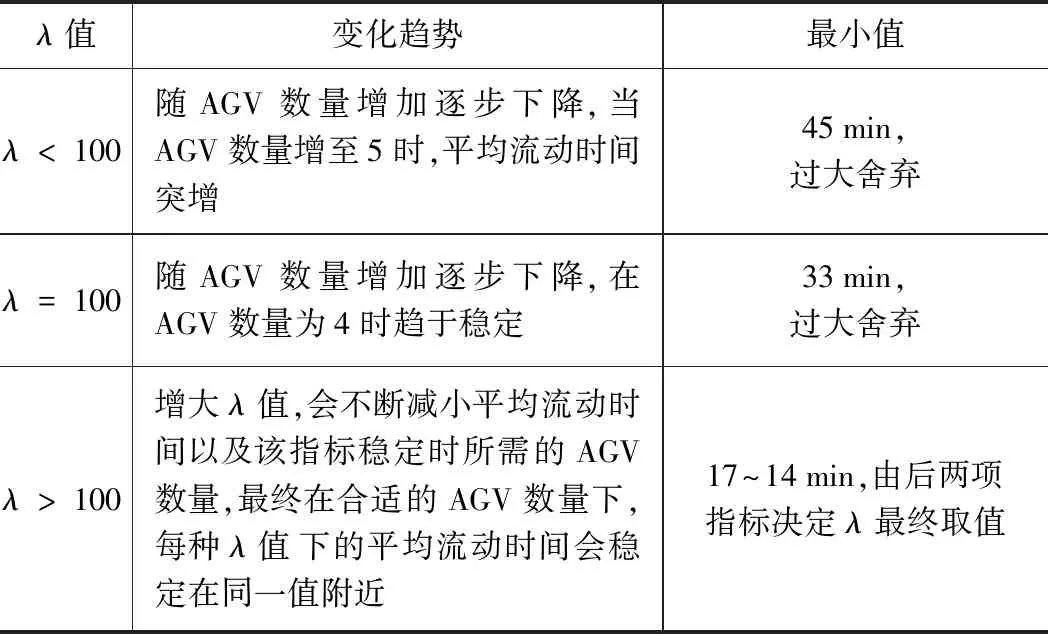
表4 不同值下平均流動時間隨AGV數量增加變化趨勢

其中λ<100時，AGV數量增至5而平均流動時間突增，這是由于各機床加工能力不足，任務投產頻率過快，工件被搬運到機床入口緩沖區的頻率也過快，工件大量堆積在入口緩沖中，等待加工時間過長所造成的。

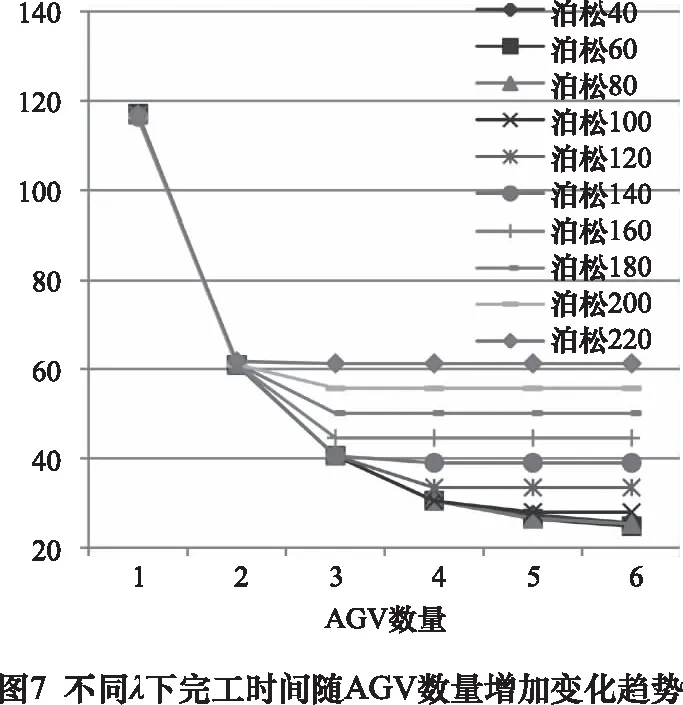
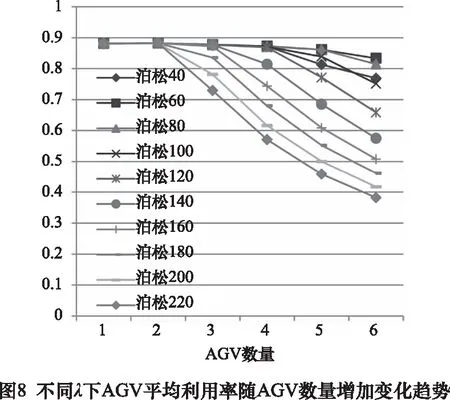
如圖7所示，相反增大任務到達時間間隔會不斷增大系統的完工時間。結合前面分析，完工時間指標下，選擇泊松120、AGV數量為4的情況為最優。從圖8可看出增大任務到達時間間隔也會不斷降低所需AGV的平均利用率，選擇泊松120、AGV數量為4的組合時AGV平均利用率為86.8%，利用率較高，應選擇數量為5時，利用率為77.2%更合適，此時指標1平均流動時間相比于AGV數量為4時的20 min也更穩定更低，為17 min，與最終的穩定值更接近。

原生產條件泊松140分布時，在AGV數量為4時各指標均達到最優，雖然其平均流動時間為16 min，利用率為81%，都比泊松120。5輛車時更好一些，實則很接近，但其完工時間高出6個多小時，最終確定最優任務到達時間間隔服從泊松120分布，最佳配置AGV數量為5。

新確定的泊松120、AGV數量為5的生產條件，可能會對已確定的最優規則造成影響，為驗證此影響是否存在及是何影響，在此條件下再次進行規則組合比較，驗證結果如圖9所示，最優規則組合仍為LWT/STT，試驗前提條件成立，此時最優規則組合下的平均流動時間值較之其他組合系統性能提升指數μ最大達到26.8%，再次證明采用STT/LWT規則組合將提升系統性能，同時也說明不同的任務到達頻率將會影響規則組合對系統性能的提升指數，也有可能改變最優規則組合：SQ路由規則由最次變為次優。兩種生產條件下系統性能穩定時的平均流動時間值相差不大，為更直觀表達改變任務到達頻率對系統性能影響，定義完工時間指標下的系統性能提升指數φ，按式(2) 計算：

(2)

得到泊松120、AGV數量為5情況下系統性能較之泊松140、AGV數量為4時提升18%。

(2)任務到達方式分析

在最優規則組合、最優任務到達時間間隔下，選擇最優任務到達方式，包含投產方式與批量兩方面內容。具體試驗內容如表5所示。

表5 任務到達方式試驗內容

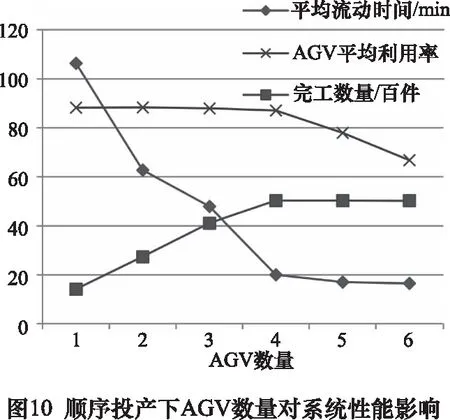
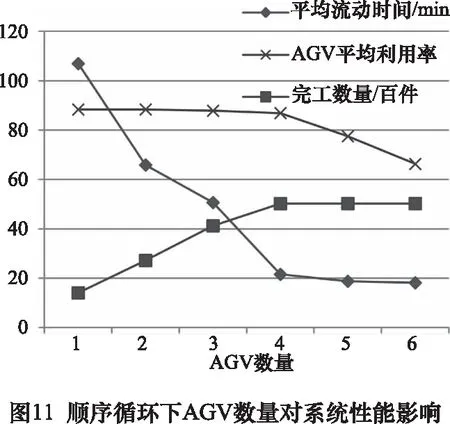
第1、2種任務到達方式下的仿真結果如圖10～11所示，在小車數量為5時，系統的加工能力分別飽和在5 030件與5 027件，相差不大，但后者工件的平均流動時間增加了近兩分鐘。故前一種到達方式更好。

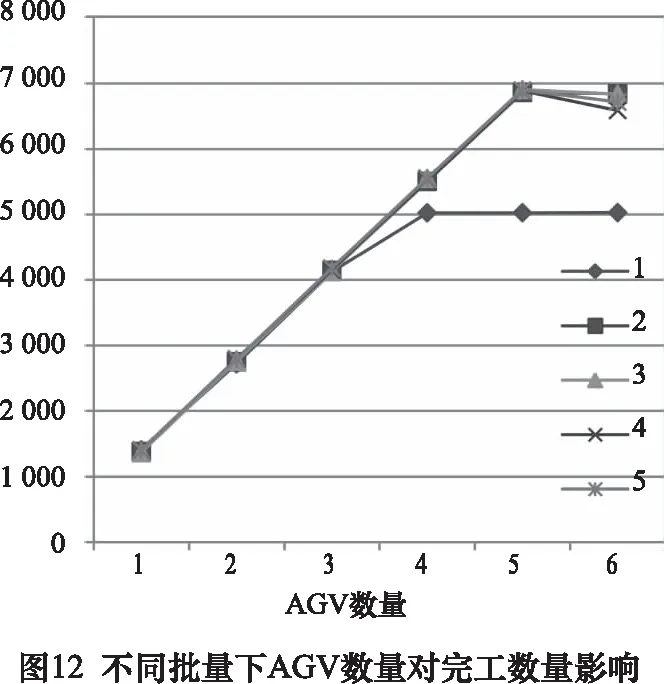
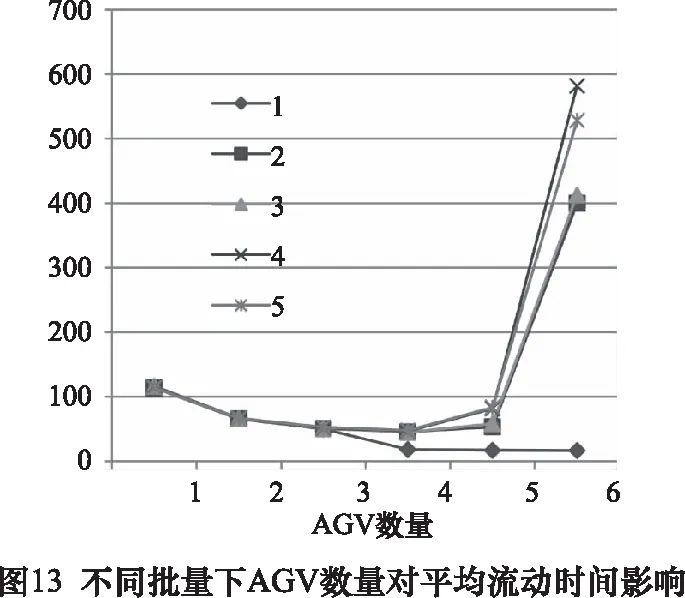
第3種到達方式下的仿真結果如圖12～13所示，結果表明在泊松120到達時間間隔下，一旦任務一次到達兩個及以上，工件在系統中的平均流動時間將大幅增加，而系統加工能力卻得不到大幅提升，這是由于工件一次到達過多而機床加工能力不足所造成的。故適應該模型最優的任務到達方式應為順序投產、批量為1。

4 結語

柔性作業車間機床與AGV聯合調度問題是典型NP難問題，求解過程具有一定復雜度，為此采用基于優先級規則組合的方法，本文考慮了工件路由規則和AGV調度規則兩方面的規則組合，基于離散事件建模與仿真方法對9種規則組合進行對比研究，結果表明，將LWT作為工件路由規則、STT作為AGV調度規則可提供良好的結果，在此種規則組合下，進一步可確定最優的任務到達模式為采用順序投產、批量為1、到達頻率服從泊松120分布，以及系統應配置AGV的最佳數量為5。在這些最優條件下，系統性能平均流動時間將縮短26.8%、完工時間將縮短18%，證明了采用合適的優先級規則組合、任務到達模式以及AGV數量可以有效解決機床與AGV聯合調度問題、優化系統生產性能。