淺析平面運動剛體的外力之功

劉延彬

【摘? ?要】? ?給出了平面運動剛體上外力之功的推導過程，分析了作用在剛體上外力之功與作用在質點上外力之功的異同，厘清了平面運動剛體的外力之功的計算過程，并且進行了例題分析及詳細討論。

【關鍵詞】? ?平面運動;剛體;功

Analysis of the External Force of a Plane Moving Rigid Body

Liu Yanbin

（Anhui University of Science and Technology， Huainan 232001，China）

【Abstract】? ? This paper gives the derivation process of work of external force acting on a plane moving rigid body， analyzes the similarities and differences between it and the work of external force acting on a particle， clarifies the calculation process of work of external force acting on a plane moving rigid body， and makes example analysis and discussion of this issue.

【Key words】? ? ?plane motion;rigid body;work

0? ? ?引言

功是描述外力在物體運動過程中的空間累積效應，是能量變化的一種量度，亦是理論力學課程的重要概念之一。作用在平面運動剛體上的外力之功與作用在質點上的外力之功計算方法具有較大的差異。作用在平面運動剛體上的力系與作用在運動質點上的力系不同，具有其特殊性。力系作用在平面運動剛體上時， 力的作用點可能相對剛體靜止， 也可能相對剛體移動，即力的作用點可能會發生變更。現有理論力學教材中，都是先給出作用于質點上的力做功的概念，然后從力系簡化出發，直接給出作用在平動剛體上力系功的計算公式[1-2]，并沒有給出具體的推導過程。計算公式說起來簡單，但是常常引起學生困惑不解，計算作用在平面運動剛體上的外力之功時往往無從下手[3-4]。

本文對作用在平面運動剛體上的力系所做的功進行討論，并厘清其與作用在質點上力系所做的功的異同，以期給理論力學初學者明晰的概念。

1? ? ?平面運動剛體的外力之功

質點[M]在變力[F]的作用下，其微小位移為[dr]，在這微小位移中，力[F]做的稱為元功，記為[δW]，則

[δW=F?dr]? （1）

剛體的平面運動可以分解為質心的平動及圍繞質心的轉動，故本文基于質心討論作用在平面運動剛體上的外力之功。令剛體受到的力系為[（F1，F2，…，Fn）]，各力的作用點分別為[（P1，P2，…，Pn）]，剛體質心C的矢徑為[rC]，剛體的角速度矢量為[ω]。剛體上任意給定點[Pk]，其速度矢量為：

[rk=vC+ω×ρk]? （2）

由于[ω=zdφ/dt]，令[dφ=zdφ]為剛體無限小角位移矢量。由（1）式可得[Pk]的無限小的位移，位移矢量[drk]與質心的無限小位移矢量[drC]和剛體無限小角位移矢量[dφ]的關系，即：

[drk=drC+dφ×ρk]? （3）

則[n]個力所做的元功之和為：

[δW=k=1nFk?（drC+dφ×ρk）? ? ?=k=1nFk?drC+k=1n（Fk×ρk）?dφ]? （4）

由靜力學可知，主矢和主矩的定義為：

[FR=k=1nFkMC=k=1n（Fk×ρk）]? （5）

且[MC]與[dφ]同向，所以（4）式可以簡化為：

[δW=FR?drC+MCdφ]? （6）

力所做的功及元功如圖1所示。從（6）式可以看出，平面運動剛體上力系的功等于力系向質心簡化所得的主矢和主矩所做的功之和。從以上推導可以看出，對于剛體平面運動，功的定義中的位移是剛體上受力質點的位移。此外，以上推導不但適用于質心為基點，而且對剛體上的任意一點為基點時仍然適用。

考慮質心的運動路徑為[l]，則力系所做的功為：

[W=lFC?drC+MCdφ=lFR?vC+MCωdt]? （7）

元功對時間的導數稱為功率，通常以P表示，其數學表達式為：

[P=δWdt]? （8）

由（6）式可得，主矢和主矩的功率方程可寫成：

[P=FR?vC+MCω]? （9）

式中[vC]是質心的速度，[ω]是平面運動剛體的角速度。

2? ? ?作用在剛體外力之功的說明

與作用在質點上的外力不同，作用在運動剛體上力的作用點可能相對剛體靜止， 也可能相對剛體移動，即力的作用點可能會發生變更。所以，需要明確與作用在質點上的力的功的異同。作用在平面運動剛體上力系所做的功分為兩項：一是主矢所做的功;二是簡化到質心上的主矩所做的功。對于一些特殊情況，作用在平面運動剛體上的外力不做功，與計算質點外力做功類似，計算作用在平動剛體上的力系做功時可以忽略不做功的力。本文針對作用在剛體上的外力之功做如下4點具體說明。

（1）[dr]是力作用質點的元位移：對于平面運動的剛體，功定義式中的位移是剛體上受力質點的元位移。

（2）力系所做的功與選擇的參考系有關：從功的推導過程可以看出，不同參考系下，相同的力系所做的功可能不相同，在不限定參考系的前提下討論一個力系所做的功并沒有意義。

（3）理想約束的約束反力不做功：理想約束力的方向與點的運動方向垂直，由功的定義式（1）可知，剛體在運動過程中，作用在剛體上的理想約束力所做的功為零。理想約束主要包括：光滑固定面約束，光滑鉸鏈、無重力桿、不可伸長柔索、固定端約束等。

（4）作用在速度瞬心上的外力不做功：對于速度瞬心，其速度[v=0]，必有[dr=vdt=0]，由元功的定義式（1）可知，作用在速度瞬心上的力不做功。

3? ? ?實例分析及討論

計算作用在平面運動剛體上力系所做功的步驟如下。

（1）畫出平面運動剛體的受力分析圖;（2）判斷剛體做平面運動過程不做功的力;（3）將做功的力向質心簡化;（4）計算主矢和主矩;（5）基于公式（7），計算力系所做的功。

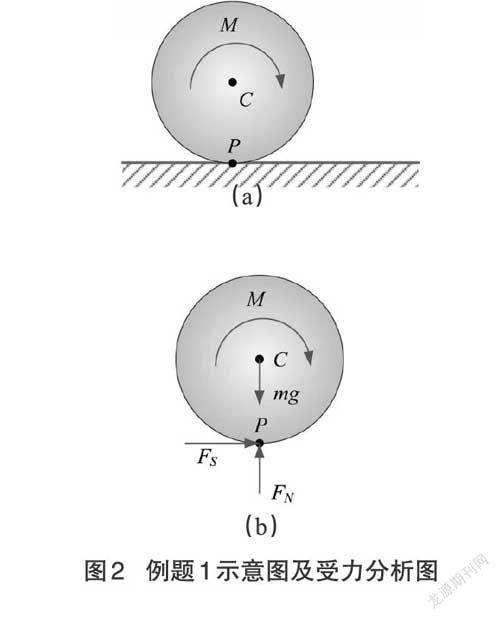
例題1? ?如圖2（a）所示，勻質圓盤質量為[m]，半徑為[R]，作用于圓盤的力偶為[M]，圓盤沿水平直線做純滾動，求當圓盤[C]走過路程[S]時圓盤所受力系的功。

解：圓盤的受力分析如圖2 （b）所示，[FS]是摩擦力，[FN]是平面的支持力。由于P點是平面運動圓盤的速度瞬心，所以[FS]與[FN]均不做功;在垂直方向上圓盤沒有位移，重力亦不做功，所以做功的只有力偶[M]，故力系所做的功為：

[W=MSR]

討論：對于摩擦力[FS]，可以將其平移至質心，證明其做功為零，[FS]對質心的力矩為：

[MC=FSR]

故摩擦力做的功為：

[WS=FSS-FSRSR=0]

可見采用（6）式計算，摩擦力[FS]做功仍為0。

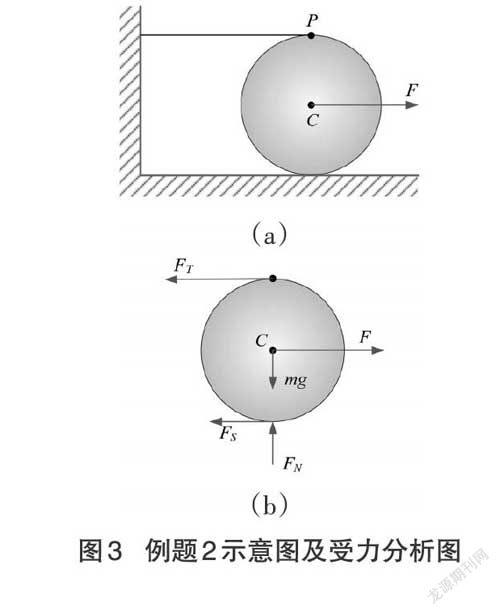
例題2? ?勻質圓盤質量為[m]，半徑為[R]，外緣上纏繞無重細繩，繩頭水平固定在墻上，如圖3（a） 所示。圓盤中心[C]點作用一個較大的力[F]，使圓盤中心[C]向右加速運動，圓盤與水平地面間滑動摩擦系數為[f]，力[F]為常量，求當圓盤[C]走過路程[S]時圓盤所受力系的功。

解：圓盤的受力分析如圖3（b） 所示。由于繩子不可伸長，圓盤的運動如同沿繩索水平方向做純滾動，故[P]點為圓盤的速度瞬心，所以繩子的拉力[FT]不做功;在垂直方向上沒有位移，故重力[mg]及支持力[FN]亦不做功。將摩擦力[FS]向質心[C]平移，則作用在圓盤上的做功的力的主矢為：[FR=F-FS]，主矩為：[MC=FSR=mgfR]（順時針）。由公式（7）可得力系所做功為：

[W=FRS+MCSR? =F-mgfS-mgfRSR=FS-2mgfS]

討論：在此題中，圓盤轉動方向為逆時針，主矩為順時針，故主矩做負功。拉力[F]僅僅在平動過程中做功，而摩擦力不但對剛體的平動做功，而且對剛體的轉動亦做功。

摩擦力做功的問題是理論力學學習中的一個難點，常常有學生產生疑問：摩擦力總阻礙物體的運動，為什么還能不做功或者做正功呢？從以上兩個實例可以看出摩擦力可以做負功，亦可以不做功。此外，對于一些情況摩擦力亦可以做正功。

4? ? ?結論

針對作用在平面運動剛體上的外力的功，本文闡述了其與作用在質點上外力的功的異同，澄清了平面運動剛體上外力功的認識誤區，得出如下具體結論：（1）[dr]是力作用質點的元位移;（2）力系所做的功與選擇的參考系有關;（3）理想約束的約束反力不做功;（4）作用在速度瞬心上的外力不做功;（5）不同情況下，平面運動剛體上的摩擦力可以做正功、負功或是不做功。

[參考文獻]

[1]? 哈爾濱工業大學理論力學教研室.理論力學（Ⅰ）[M].北京：高等教育出版社，2016：259-280.

[2]? 洪嘉振，楊長俊.理論力學[M].北京：高等教育出版社，2015：230-238.

[3]? 張春麗，張巖.PBL教學模式在《工程力學》課程中的應用[J].廊坊師范學院學報（自然科學版），2016，16（4）：120-122.

[4]? 何敏，江燕燕.力學模型蹺蹺板的教學研究[J].廊坊師范學院學報（自然科學版），2020，20（2）：108-118.